Análisis de supervivencia

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Subdivisión de estadísticas

análisis de supervivencia es una rama de la estadística que analiza la duración esperada del tiempo hasta que ocurre un evento, como la muerte en organismos biológicos y fallas en sistemas mecánicos. Este tema se llama teoría de la confiabilidad o análisis de confiabilidad en ingeniería, análisis de duración o modelado de duración en economía, y análisis de la historia de eventos en sociología. El análisis de supervivencia intenta responder ciertas preguntas, como ¿cuál es la proporción de una población que sobrevivirá después de un tiempo determinado? De los que sobrevivan, ¿a qué ritmo morirán o fracasarán? ¿Se pueden tener en cuenta múltiples causas de muerte o fracaso? ¿Cómo aumentan o disminuyen las circunstancias o características particulares la probabilidad de supervivencia?

Para responder a estas preguntas, es necesario definir "vida". En el caso de la supervivencia biológica, la muerte es inequívoca, pero en el caso de la confiabilidad mecánica, el fallo puede no estar bien definido, pues bien puede haber sistemas mecánicos en los que el fallo sea parcial, una cuestión de grado o no esté localizado en el tiempo. Incluso en los problemas biológicos, algunos acontecimientos (por ejemplo, un ataque cardíaco u otra insuficiencia orgánica) pueden tener la misma ambigüedad. La teoría que se describe a continuación supone eventos bien definidos en momentos específicos; otros casos pueden tratarse mejor mediante modelos que tengan en cuenta explícitamente acontecimientos ambiguos.

De manera más general, el análisis de supervivencia implica el modelado de datos de tiempo hasta el evento; En este contexto, la muerte o el fracaso se consideran un "evento" En la literatura sobre análisis de supervivencia, tradicionalmente sólo ocurre un evento para cada sujeto, después del cual el organismo o mecanismo muere o se rompe. Los modelos de evento recurrente o de evento repetido relajan esa suposición. El estudio de eventos recurrentes es relevante en la confiabilidad de los sistemas y en muchas áreas de las ciencias sociales y la investigación médica.

Introducción al análisis de supervivencia

El análisis de supervivencia se utiliza de varias maneras:

Para describir los tiempos de supervivencia de los miembros de un grupo
- Tablas de vida
- Curvas Kaplan-Meier
- Función de supervivencia
- Función de peligro
Para comparar los tiempos de supervivencia de dos o más grupos
- Prueba de registro
Para describir el efecto de variables categóricas o cuantitativas sobre supervivencia
- Regreso de los riesgos proporcionales cox
- Modelos de supervivencia paramétrica
- Árboles de supervivencia
- Supervivencia de bosques aleatorios

Definiciones de términos comunes en el análisis de supervivencia

Did you mean:

The following terms are commonly used in survival analysis:

Evento: Muerte, aparición de enfermedades, recurrencia de enfermedades, recuperación u otra experiencia de interés
Tiempo: El tiempo desde el comienzo de un período de observación (como cirugía o tratamiento inicial) a (i) un evento, o (ii) final del estudio, o (iii) pérdida de contacto o retiro del estudio.
Censoring / Observación censurada: La censura ocurre cuando tenemos alguna información sobre el tiempo de supervivencia individual, pero no sabemos exactamente el tiempo de supervivencia. El tema es censurado en el sentido de que nada se observa ni se conoce sobre ese tema después del tiempo de censura. Un sujeto censurado puede o no tener un evento después del fin del tiempo de observación.
Función de supervivencia S(t): La probabilidad de que un sujeto sobreviva más tiempo que el tiempo t.

Ejemplo: datos de supervivencia de leucemia mielógena aguda

Este ejemplo utiliza el conjunto de datos de supervivencia de la leucemia mielógena aguda "aml" del programa de "supervivencia" paquete en R. El conjunto de datos es de Miller (1997) y la pregunta es si el ciclo estándar de quimioterapia debe extenderse ('mantenerse') durante ciclos adicionales.

El conjunto de datos de aml ordenados por tiempo de supervivencia se muestra en el cuadro.

El tiempo es indicado por la variable "tiempo", que es el tiempo de supervivencia o censura
El evento (recurrencia del cáncer de aml) se indica por la variable "status". 0= no evento (censored), 1= evento (recurrencia)
Grupo de tratamiento: la variable "x" indica si se administra quimioterapia de mantenimiento

La última observación (11), a las 161 semanas, está censurada. La censura indica que el paciente no tuvo ningún evento (no hubo recurrencia del cáncer de aml). Otro sujeto, la observación 3, fue censurado a las 13 semanas (indicado por estado = 0). Este sujeto estuvo en el estudio solo durante 13 semanas y el cáncer de aml no recurrió durante esas 13 semanas. Es posible que este paciente fuera inscrito cerca del final del estudio, por lo que pudo ser observado durante sólo 13 semanas. También es posible que el paciente haya sido inscrito tempranamente en el estudio, pero se haya perdido durante el seguimiento o se haya retirado del estudio. La tabla muestra que otros sujetos fueron censurados a las 16, 28 y 45 semanas (observaciones 17, 6 y 9 con estado=0). Todos los sujetos restantes experimentaron eventos (recurrencia de cáncer de aml) durante el estudio. La cuestión de interés es si la recurrencia ocurre más tarde en pacientes mantenidos que en pacientes no mantenidos.

Gráfico de Kaplan-Meier para los datos de aml

La función de supervivencia S(t), es la probabilidad de que un sujeto sobreviva más tiempo que el tiempo t. S(t) es teóricamente una curva suave, pero generalmente se estima utilizando la curva de Kaplan-Meier (KM). El gráfico muestra la gráfica de KM para los datos de aml y se puede interpretar de la siguiente manera:

El x axis es tiempo, desde cero (cuando la observación comenzó) hasta el último punto de tiempo observado.
El Sí. axis es la proporción de sujetos que sobreviven. A tiempo cero, el 100% de los sujetos están vivos sin un evento.
La línea sólida (similar a una escalera) muestra la progresión de los acontecimientos.
Una caída vertical indica un evento. En la tabla de aml mostrada anteriormente, dos sujetos tuvieron eventos a las cinco semanas, dos tuvieron eventos a las ocho semanas, uno tuvo un evento a las nueve semanas, y así sucesivamente. Estos eventos a las cinco semanas, ocho semanas y así sucesivamente se indican por las caídas verticales en la parcela KM en esos puntos de tiempo.
En el extremo derecho de la trama KM hay una marca de garrapata a 161 semanas. La marca vertical indica que un paciente fue censurado en este momento. En el cuadro de datos de aml se censuraron cinco temas, a las 13, 16, 28, 45 y 161 semanas. Hay cinco marcas en la trama KM, correspondientes a estas observaciones censuradas.

Tabla de vida para los datos de aml

Una tabla de vida resume los datos de supervivencia en términos del número de eventos y la proporción de supervivientes en cada momento del evento. Se muestra la tabla de vida para los datos de aml, creada con el software R .

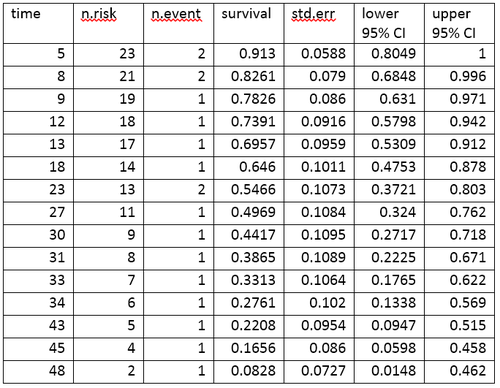
La tabla de vida resume los eventos y la proporción de supervivientes en cada momento del evento. Las columnas de la tabla de vida tienen la siguiente interpretación:

tiempo da los puntos de tiempo en los que ocurren los eventos.
n.risk es el número de sujetos en riesgo inmediatamente antes del momento, t. Ser "en riesgo" significa que el sujeto no ha tenido un evento antes del tiempo t, y no es censurado antes o en el momento t.
n.event es el número de sujetos que tienen eventos a la vez t.
La supervivencia es la proporción sobreviviente, según se determina utilizando la estimación del límite de productos Kaplan-Meier.
std.err es el error estándar de la supervivencia estimada. El error estándar de la estimación del límite de productos Kaplan-Meier se calcula utilizando la fórmula de Greenwood, y depende del número en riesgo (n.risk en la tabla), el número de muertes (n.evento en la tabla) y la proporción sobreviviente (supervivencia en la tabla).
El IC del 95% inferior y el IC superior del 95% son los límites de confianza inferiores y superiores del 95% para la proporción sobreviviente.

Prueba de rango logarítmico: prueba de diferencias en la supervivencia en los datos de aml

La prueba de rango logarítmico compara los tiempos de supervivencia de dos o más grupos. Este ejemplo utiliza una prueba de rango logarítmico para una diferencia en la supervivencia en los grupos de tratamiento mantenido versus no mantenido en los datos de aml. El gráfico muestra gráficos de KM para los datos de aml desglosados por grupo de tratamiento, que se indica con la variable "x" en los datos.

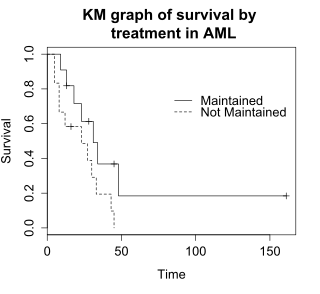
La hipótesis nula para una prueba de rangos logarítmicos es que los grupos tienen la misma supervivencia. El número esperado de sujetos que sobreviven en cada momento de cada evento se ajusta al número de sujetos en riesgo en los grupos en cada momento del evento. La prueba de rango logarítmico determina si el número observado de eventos en cada grupo es significativamente diferente del número esperado. La prueba formal se basa en una estadística de chi-cuadrado. Cuando la estadística de rango logarítmico es grande, es evidencia de una diferencia en los tiempos de supervivencia entre los grupos. La estadística de rango logarítmico tiene aproximadamente una distribución de Chi-cuadrado con un grado de libertad, y el valor p se calcula mediante la prueba de Chi-cuadrado.

Para los datos de ejemplo, la prueba de rango logarítmico para la diferencia en la supervivencia da un valor p de p=0,0653, lo que indica que los grupos de tratamiento no difieren significativamente en la supervivencia, suponiendo un nivel alfa de 0,05. El tamaño de la muestra de 23 sujetos es modesto, por lo que hay poco poder para detectar diferencias entre los grupos de tratamiento. La prueba de chi-cuadrado se basa en una aproximación asintótica, por lo que el valor p debe considerarse con precaución para tamaños de muestra pequeños.

Análisis de regresión de riesgos proporcionales (PH) de Cox

Las curvas de Kaplan-Meier y las pruebas de rango logarítmico son más útiles cuando la variable predictiva es categórica (p. ej., fármaco versus placebo) o toma una pequeña cantidad de valores (p. ej., dosis de fármaco 0, 20, 50 y 100). mg/día) que pueden ser tratados como categóricos. La prueba de rango logarítmico y las curvas KM no funcionan fácilmente con predictores cuantitativos como la expresión genética, el recuento de glóbulos blancos o la edad. Para variables predictivas cuantitativas, un método alternativo es el análisis de regresión de riesgos proporcionales de Cox. Los modelos Cox PH también funcionan con variables predictoras categóricas, que están codificadas como indicador {0,1} o variables ficticias. La prueba de rango logarítmico es un caso especial de análisis de Cox PH y se puede realizar utilizando el software Cox PH.

Ejemplo: análisis de regresión de riesgos proporcionales de Cox para melanoma

Este ejemplo utiliza el conjunto de datos sobre melanoma del Capítulo 14 de Dalgaard.

Los datos están en el paquete R ISwR. La regresión de riesgos proporcionales de Cox utilizando R proporciona los resultados que se muestran en el cuadro.

Los resultados de la regresión de Cox se interpretan de la siguiente manera.

El sexo es codificado como un vector numérico (1: hembra, 2: macho). La RResumen para el modelo Cox da la relación de riesgo (HR) para el segundo grupo relativo al primer grupo, es decir, masculino versus femenino.
coef = 0.662 es el logaritmo estimado de la relación de peligro para hombres contra mujeres.
exp(coef) = 1.94 = exp(0.662) - El registro de la relación de peligro (coef= 0.662) se transforma a la relación de riesgo utilizando exp(coef). El resumen para el modelo Cox da la relación de riesgo para el segundo grupo en relación con el primer grupo, es decir, masculino versus femenino. La relación de riesgo estimada de 1,94 indica que los hombres tienen un mayor riesgo de muerte (tasas de supervivencia más bajas) que las mujeres, en esos datos.
se(coef) = 0.265 es el error estándar de la relación de riesgo de registro.
z = 2,5 = coef/se(coef) = 0.662/0.265. Dividir el coef por su error estándar da la puntuación z.
p=0.013. El valor p correspondiente a z=2.5 para el sexo es p=0.013, indicando que hay una diferencia significativa en la supervivencia como función del sexo.

El resultado resumido también proporciona intervalos de confianza superior e inferior del 95 % para el índice de riesgo: límite inferior del 95 % = 1,15; límite superior del 95% = 3,26.

Finalmente, el resultado proporciona valores p para tres pruebas alternativas para la significancia general del modelo:

Test de relación de probabilidad = 6.15 en 1 df, p=0.0131
Prueba de Wald = 6.24 en 1 df, p=0.0125
Prueba de puntuación (log-rank) = 6.47 en 1 df, p=0.0110

Estas tres pruebas son asintóticamente equivalentes. Para N lo suficientemente grande, darán resultados similares. Para N pequeño, pueden diferir algo. La última fila, "Prueba de puntuación (logrank)" es el resultado de la prueba de rangos logarítmicos, con p=0,011, el mismo resultado que la prueba de rangos logarítmicos, porque la prueba de rangos logarítmicos es un caso especial de una regresión PH de Cox. La prueba de razón de verosimilitud se comporta mejor para tamaños de muestra pequeños, por lo que generalmente se prefiere.

Modelo de Cox utilizando una covariable en los datos de melanoma

El modelo de Cox amplía la prueba de rango logarítmico al permitir la inclusión de covariables adicionales. Este ejemplo utiliza el conjunto de datos de melanoma donde las variables predictoras incluyen una covariable continua, el grosor del tumor (nombre de la variable = "grueso").

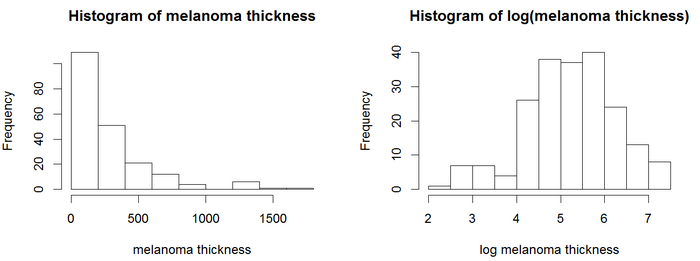
En los histogramas, los valores de espesor están sesgados positivamente y no tienen una distribución de probabilidad simétrica similar a Gauss. Los modelos de regresión, incluido el modelo de Cox, generalmente dan resultados más confiables con variables distribuidas normalmente. Para este ejemplo podemos usar una transformada logarítmica. El logaritmo del espesor del tumor parece tener una distribución más normal, por lo que los modelos de Cox utilizarán el logaritmo del espesor. El análisis de PH de Cox proporciona los resultados en el cuadro.

El valor p de las tres pruebas generales (probabilidad, Wald y puntuación) es significativo, lo que indica que el modelo es significativo. El valor p para log(grueso) es 6,9e-07, con un índice de riesgo HR = exp(coef) = 2,18, lo que indica una fuerte relación entre el espesor del tumor y un mayor riesgo de muerte.

Por el contrario, el valor p para el sexo ahora es p=0,088. El índice de riesgo HR = exp(coef) = 1,58, con un intervalo de confianza del 95% de 0,934 a 2,68. Debido a que el intervalo de confianza para la FC incluye 1, estos resultados indican que el sexo hace una contribución menor a la diferencia en la FC después de controlar el grosor del tumor, y solo tiene una tendencia hacia la significación. El examen de los gráficos de log(grosor) por sexo y una prueba t de log(grosor) por sexo indican que existe una diferencia significativa entre hombres y mujeres en el espesor del tumor cuando consultan por primera vez al médico.

El modelo de Cox supone que los riesgos son proporcionales. El supuesto de riesgo proporcional se puede probar utilizando la función R cox.zph(). Un valor p inferior a 0,05 indica que los riesgos no son proporcionales. Para los datos de melanoma obtenemos p=0,222. Por tanto, no podemos rechazar la hipótesis nula de que los riesgos son proporcionales. En los libros de texto citados se describen pruebas y gráficos adicionales para examinar un modelo de Cox.

Extensiones a los modelos Cox

Los modelos de Cox se pueden ampliar para abordar variaciones del análisis simple.

Estratificación. Los sujetos pueden dividirse en estratos, donde se espera que los sujetos dentro de un estrato sean relativamente más similares entre sí que a los sujetos elegidos aleatoriamente de otros estratos. Se supone que los parámetros de regresión son los mismos en los estratos, pero puede existir un peligro de referencia diferente para cada estrato. La estratificación es útil para los análisis que utilizan sujetos emparejados, para tratar con subconjuntos de pacientes, como diferentes clínicas, y para tratar con violaciones de la suposición proporcional de peligro.
Variando tiempo covaria. Algunas variables, como el género y el grupo de tratamiento, generalmente permanecen iguales en un ensayo clínico. Otras variables clínicas, como los niveles de proteína sérica o la dosis de medicamentos concomitantes, pueden cambiar en el curso de un estudio. Los modelos de cox se pueden ampliar para estos covariados de tiempo.

Modelos de supervivencia estructurados en árbol

El modelo de regresión PH de Cox es un modelo lineal. Es similar a la regresión lineal y la regresión logística. Específicamente, estos métodos suponen que una sola línea, curva, plano o superficie es suficiente para separar grupos (vivos, muertos) o para estimar una respuesta cuantitativa (tiempo de supervivencia).

En algunos casos, las particiones alternativas proporcionan una clasificación o estimaciones cuantitativas más precisas. Un conjunto de métodos alternativos son los modelos de supervivencia estructurados en árboles, incluidos los bosques aleatorios de supervivencia. Los modelos de supervivencia estructurados en árboles pueden dar predicciones más precisas que los modelos de Cox. Examinar ambos tipos de modelos para un conjunto de datos determinado es una estrategia razonable.

Ejemplo de análisis de árbol de supervivencia

Este ejemplo de análisis de árbol de supervivencia utiliza el paquete R "rpart". El ejemplo se basa en 146 pacientes con cáncer de próstata en estadio C en el conjunto de datos stagec de la parte. Rpart y el ejemplo de stagec se describen en Atkinson y Therneau (1997), que también se distribuye como una viñeta del paquete rpart.

Las variables por etapas son:

pgtime: tiempo de progresión, o último seguimiento libre de progresión
pgstat: status at last follow-up (1=progressed, 0=censored)
Edad: edad para el diagnóstico
eet: terapia endocrina temprana (1=no, 0=yes)
Ploidy: patrón de ADN diploide/tetraploid/aneuploid
g2: % de las células en fase G2
grado: grado tumoral (1-4)
gleason: Grado Gleason (3-10)

El árbol de supervivencia producido por el análisis se muestra en la figura.

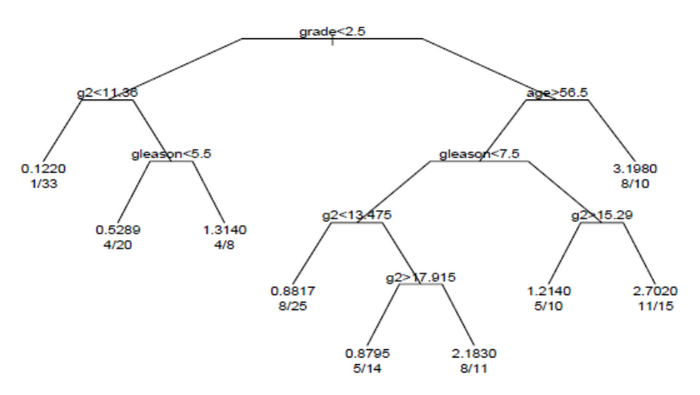
Cada rama del árbol indica una división del valor de una variable. Por ejemplo, la raíz del árbol divide las materias con calificación < 2,5 versus sujetos con nota 2,5 o superior. Los nodos terminales indican la cantidad de sujetos en el nodo, la cantidad de sujetos que tienen eventos y la tasa relativa de eventos en comparación con la raíz. En el nodo del extremo izquierdo, los valores 1/33 indican que uno de los 33 sujetos en el nodo tuvo un evento y que la tasa relativa de eventos es 0,122. En el nodo del extremo inferior derecho, los valores 11/15 indican que 11 de 15 sujetos en el nodo tuvieron un evento y la tasa relativa de eventos es 2,7.

Bosques aleatorios de supervivencia

Una alternativa a la creación de un único árbol de supervivencia es crear muchos árboles de supervivencia, donde cada árbol se construye utilizando una muestra de los datos y se promedian los árboles para predecir la supervivencia. Este es el método subyacente a los modelos forestales aleatorios de supervivencia. El análisis aleatorio de supervivencia del bosque está disponible en el paquete R "randomForestSRC".

El paquete randomForestSRC incluye un ejemplo de análisis de bosque aleatorio de supervivencia utilizando el conjunto de datos pbc. Estos datos provienen del ensayo de cirrosis biliar primaria (CBP) del hígado de Mayo Clinic realizado entre 1974 y 1984. En el ejemplo, el modelo de supervivencia del bosque aleatorio proporciona predicciones de supervivencia más precisas que el modelo de Cox PH. Los errores de predicción se estiman mediante remuestreo de arranque.

Modelos de supervivencia de aprendizaje profundo

Los avances recientes en el aprendizaje de representación profunda se han extendido a la estimación de supervivencia. El modelo DeepSurv propone reemplazar la parametrización log-lineal del modelo CoxPH con un perceptrón multicapa. Otras extensiones, como Deep Survival Machines y Deep Cox Mixtures, implican el uso de modelos de mezcla de variables latentes para modelar la distribución del tiempo hasta el evento como una mezcla de distribuciones paramétricas o semiparamétricas mientras se aprenden conjuntamente representaciones de las covariables de entrada. Los enfoques de aprendizaje profundo han demostrado un rendimiento superior, especialmente en modalidades de datos de entrada complejas, como imágenes y series temporales clínicas.

Formulación general

Función de supervivencia

El objeto de interés principal es la función de supervivencia, convencionalmente denotada S, que se define como

t)}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">S()t)=Pr()T■t){displaystyle S(t)=Pr(T]}t)}" aria-hidden="true" class="mwe-math-fallback-image-display" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/05d2a976ead3cc144745135a447130aac75be7f2" style="vertical-align: -0.838ex; width:17.125ex; height:2.843ex;"/>

tTtfunción de supervivenciafunción de supervivenciafunción de confiabilidadRt

Por lo general, se supone que S(0) = 1, aunque podría ser menor que 1 si existe la posibilidad de muerte o falla inmediata.

La función de supervivencia debe ser no creciente: S(u) ≤ S(t) si u ≥ t. Esta propiedad se sigue directamente porque T>u implica T>t. Esto refleja la noción de que la supervivencia hasta una edad posterior sólo es posible si se alcanzan todas las edades más tempranas. Dada esta propiedad, la función de distribución de vida y la densidad de eventos (F y f a continuación) están bien definidas.

Generalmente se supone que la función de supervivencia se acerca a cero a medida que la edad aumenta sin límite (es decir, S(t) → 0 cuando t → ∞), aunque el límite podría ser mayor que cero si la vida eterna es posible. Por ejemplo, podríamos aplicar el análisis de supervivencia a una mezcla de isótopos de carbono estables e inestables; Los isótopos inestables se desintegrarían tarde o temprano, pero los isótopos estables durarían indefinidamente.

Función de distribución de vida y densidad de eventos

Las cantidades relacionadas se definen en términos de la función de supervivencia.

La función de distribución de la vida útil, convencionalmente denotada como F, se define como el complemento de la función de supervivencia,

{displaystyle F(t)=Pr(Tleq t)=1-S(t).}

{displaystyle f(t)=F'(t)={frac {d}{dt}}F(t).}

fdensidad del evento

La función de supervivencia se puede expresar en términos de distribución de probabilidad y funciones de densidad de probabilidad.

t)=int _{t}^{infty }f(u),du=1-F(t).}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">S()t)=Pr()T■t)=∫ ∫ tJUEGO JUEGO f()u)du=1− − F()t).{displaystyle S(t)=Pr(T]=int _{t}{infty }f(u),du=1-F(t). }t)=int _{t}^{infty }f(u),du=1-F(t).}" aria-hidden="true" class="mwe-math-fallback-image-display" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/0b463abddfd24a5cc9132d2752860d15df449af6" style="vertical-align: -2.338ex; width:44.438ex; height:5.843ex;"/>

{displaystyle s(t)=S'(t)={frac {d}{dt}}S(t)={frac {d}{dt}}int _{t}^{infty }f(u),du={frac {d}{dt}}[1-F(t)]=-f(t).}

Función de riesgo y función de riesgo acumulativo

El función de peligro, convencionalmente denotado $lambda$ o $h$ , se define como la tasa de evento a tiempo $t$ condicional a la supervivencia hasta el tiempo $t$ o más tarde (es decir, ${displaystyle Tgeq t}$ ). Supongamos que un artículo ha sobrevivido por un tiempo $t$ y deseamos la probabilidad de que no sobreviva por un tiempo adicional $dt$ :

<math alttext="{displaystyle h(t)=lim _{dtrightarrow 0}{frac {Pr(tleq Th()t)=limdt→ → 0Pr()t≤ ≤ T.t+dt)dt⋅ ⋅ S()t)=f()t)S()t)=− − S.()t)S()t).{displaystyle h(t)=lim _{dtrightarrow 0}{frac {Pr(tleq T didt+dt)}{dtcdot S(t)}={frac {f(t)}{S(t)}=-{frac {S(t)}{S(t)}} {<img alt="{displaystyle h(t)=lim _{dtrightarrow 0}{frac {Pr(tleq T

función de peligro

mu

tasa de peligro

La fuerza de mortalidad de la función de supervivencia se define como ${displaystyle mu (x)=-{d over dx}ln(S(x))={frac {f(x)}{S(x)}}}$

La fuerza de la mortalidad también se llama la fuerza del fracaso. Es la función de densidad de probabilidad de la distribución de la mortalidad.

En ciencias actuariales, la tasa de peligrosidad es la tasa de muerte para las vidas envejecidas $x$ . Por una vida envejecida $x$ , la fuerza de la mortalidad $t$ años más tarde es la fuerza de mortalidad para un ${displaystyle (x+t)}$ - años. La tasa de riesgo también se denomina tasa de fracaso. La tasa de riesgo y la tasa de fracaso son nombres utilizados en la teoría de la fiabilidad.

Cualquier función $h$ es una función de peligro si y sólo si satisface las siguientes propiedades:

${displaystyle forall xgeq 0left(h(x)geq 0right)}$
${displaystyle int _{0}^{infty }h(x)dx=infty }$ .

De hecho, la tasa de riesgo suele ser más informativa sobre el mecanismo subyacente del fallo que las otras representaciones de una distribución a lo largo de la vida.

La función de peligro debe ser no negativa, ${displaystyle lambda (t)geq 0}$ , y su integral sobre $[0,infty ]$ debe ser infinito, pero no se limita de otra manera; puede ser creciente o decreciente, no monotónico, o discontinuo. Un ejemplo es la función de riesgo de la curva de la bañera, que es grande para los pequeños valores de $t$ , disminuyendo a un mínimo, y posteriormente aumentando de nuevo; esto puede modelar la propiedad de algunos sistemas mecánicos para fallar poco después de la operación, o mucho más tarde, a medida que el sistema envejece.

La función de peligro puede representarse alternativamente en términos de la función acumulativa de peligro, convencionalmente denotado $Lambda$ o $H$ :

{displaystyle ,Lambda (t)=-log S(t)}

{displaystyle ,S(t)=exp(-Lambda (t))}

{displaystyle {frac {d}{dt}}Lambda (t)=-{frac {S'(t)}{S(t)}}=lambda (t).}

{displaystyle Lambda (t)=int _{0}^{t}lambda (u),du}

De la definición $Lambda (t)$ , vemos que aumenta sin límites t tiende a la infinidad (asumiendo que $S(t)$ tiende a cero). Esto implica que $lambda (t)$ no debe disminuir demasiado rápidamente, ya que, por definición, el peligro acumulativo tiene que divergir. Por ejemplo, $exp(-t)$ no es la función de peligro de ninguna distribución de supervivencia, porque su integral converge a 1.

La función de supervivencia $S(t)$ , la función de peligro acumulativo $Lambda (t)$ , la densidad $f(t)$ , la función de peligro $lambda (t)$ , y la función de distribución de la vida $F(t)$ se relacionan con

0.}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">S()t)=exp⁡ ⁡ [− − ▪ ▪ ()t)]=f()t)λ λ ()t)=1− − F()t),t■0.{displaystyle S(t)=exp[-Lambda (t)]={frac {f(t)}{lambda (t)}=1-F(t),quad t]0.}0.}" aria-hidden="true" class="mwe-math-fallback-image-display" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/17e4e85965ac80b7f00e988635a4d8253be2cd6d" style="vertical-align: -2.671ex; width:46.696ex; height:6.509ex;"/>

Cantidades derivadas de la distribución de supervivencia

Vida futura en un momento dado $t_{0}$ es el tiempo restante hasta la muerte, dada supervivencia a la edad $t_{0}$ . Así es. $T-t_{0}$ en la notación actual. El vida futura es el valor esperado de la vida futura. La probabilidad de muerte a o antes de la edad $t_{0}+t$ , dada supervivencia hasta la edad $t_{0}$ , es sólo

t_{0})={frac {P(t_{0}t_{0})}}={frac {F(t_{0}+t)-F(t_{0})}{S(t_{0})}}.}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">P()T≤ ≤ t0+t▪ ▪ T■t0)=P()t0.T≤ ≤ t0+t)P()T■t0)=F()t0+t)− − F()t0)S()t0).{displaystyle P(Tleq t_{0}+tmid T consistentet_{0}={frac {P(t_{0}cantadoTleq {fnMicroc {F(t_{0}}}}}}} {f}}}}}} {S(t_{0}}}}}}} {S(t_{0}}}}} {0}}}}{0}} {0}}} {0}}}{0}}}}{0}}} {0}}}}} {t_{0})={frac {P(t_{0}t_{0})}}={frac {F(t_{0}+t)-F(t_{0})}{S(t_{0})}}.}" aria-hidden="true" class="mwe-math-fallback-image-display" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/bf888ff96667a43dce778fd227b3a75f79c9473c" style="vertical-align: -2.671ex; width:67.209ex; height:6.509ex;"/>

{displaystyle {frac {d}{dt}}{frac {F(t_{0}+t)-F(t_{0})}{S(t_{0})}}={frac {f(t_{0}+t)}{S(t_{0})}}}

{displaystyle {frac {1}{S(t_{0})}}int _{0}^{infty }t,f(t_{0}+t),dt={frac {1}{S(t_{0})}}int _{t_{0}}^{infty }S(t),dt,}

Para $t_{0}=0$ , es decir, al nacer, esto reduce a la vida esperada.

En problemas de confiabilidad, la vida útil esperada se denomina tiempo medio hasta el fallo, y la vida útil futura esperada se denomina vida útil residual media.

Como la probabilidad de que un individuo sobreviva hasta la edad t o más tarde es S(t), por definición, el número esperado de supervivientes a la edad t de una población inicial de n recién nacidos es n × S(t), suponiendo la misma función de supervivencia para todos los individuos. Por tanto, la proporción esperada de supervivientes es S(t). Si la supervivencia de diferentes individuos es independiente, el número de supervivientes a la edad t tiene una distribución binomial con parámetros n y S( t), y la varianza de la proporción de supervivientes es S(t) × (1-S( t))/n.

La edad a la que permanece una proporción específica de supervivientes se puede encontrar resolviendo la ecuación S(t) = q para t, donde q es el cuantil en cuestión. Normalmente uno está interesado en la vida media, para la cual q = 1/2, u otros cuantiles como q = 0,90 o q = 0,99.

Censura

La censura es una forma de problema de datos faltantes en el que no se observa el tiempo transcurrido hasta el evento por motivos tales como la finalización del estudio antes de que todos los sujetos reclutados hayan mostrado el evento de interés o el sujeto haya abandonado el estudio antes de experimentar un evento. La censura es común en el análisis de supervivencia.

Si sólo se conoce el límite inferior l para el tiempo real del evento T de modo que T > l, esto se llama censura de derecha. La censura correcta se producirá, por ejemplo, para aquellos sujetos cuya fecha de nacimiento se conoce pero que todavía están vivos cuando se les pierde el seguimiento o cuando finaliza el estudio. Generalmente nos encontramos con datos censurados por la derecha.

Si el evento de interés ya ocurrió antes de que el sujeto fuera incluido en el estudio pero no se sabe cuándo ocurrió, se dice que los datos están censurados a la izquierda. Cuando sólo se puede decir que el evento ocurrió entre dos observaciones o exámenes, se trata de censura por intervalos.

La censura izquierda ocurre, por ejemplo, cuando un diente permanente ya ha emergido antes del inicio de un estudio odontológico que tiene como objetivo estimar su distribución de aparición. En el mismo estudio, el tiempo de emergencia se censura por intervalos cuando el diente permanente está presente en la boca en el examen actual pero aún no en el examen anterior. La censura por intervalos ocurre a menudo en los estudios sobre VIH/SIDA. De hecho, el tiempo transcurrido hasta la seroconversión del VIH sólo puede determinarse mediante una evaluación de laboratorio que normalmente se inicia después de una visita al médico. Entonces sólo se puede concluir que la seroconversión del VIH se ha producido entre dos exámenes. Lo mismo ocurre con el diagnóstico del SIDA, que se basa en los síntomas clínicos y debe confirmarse mediante un examen médico.

También puede suceder que los sujetos con una vida inferior a cierto umbral no sean observados en absoluto: esto se llama truncamiento. Tenga en cuenta que el truncamiento es diferente de la censura por la izquierda, ya que para un dato censurado por la izquierda, sabemos que el sujeto existe, pero para un dato truncado, es posible que desconozcamos por completo al sujeto. El truncamiento también es común. En el llamado estudio de entrada retrasada, los sujetos no son observados en absoluto hasta que alcanzan una determinada edad. Por ejemplo, es posible que las personas no sean observadas hasta que hayan alcanzado la edad para ingresar a la escuela. Se desconoce si hay sujetos fallecidos en el grupo de edad preescolar. Los datos truncados a la izquierda son comunes en el trabajo actuarial para seguros de vida y pensiones.

Los datos censurados a la izquierda pueden ocurrir cuando el tiempo de supervivencia de una persona se vuelve incompleto en el lado izquierdo del período de seguimiento de la persona. Por ejemplo, en un ejemplo epidemiológico, podemos monitorear a un paciente para detectar un trastorno infeccioso a partir del momento en que la prueba de la infección da positivo. Aunque podemos conocer el lado derecho de la duración del interés, es posible que nunca sepamos el tiempo exacto de exposición al agente infeccioso.

Ajustar parámetros a los datos

Los modelos de supervivencia pueden considerarse útiles como modelos de regresión ordinarios en los que la variable de respuesta es el tiempo. Sin embargo, la censura complica el cálculo de la función de probabilidad (necesaria para ajustar parámetros o hacer otros tipos de inferencias). La función de probabilidad de un modelo de supervivencia, en presencia de datos censurados, se formula de la siguiente manera. Por definición, la función de verosimilitud es la probabilidad condicional de los datos dados los parámetros del modelo. Se acostumbra suponer que los datos son independientes dados los parámetros. Entonces la función de verosimilitud es el producto de la verosimilitud de cada dato. Es conveniente dividir los datos en cuatro categorías: sin censura, censurados por la izquierda, censurados por la derecha y censurados por intervalos. Estos se denominan "unc.", "l.c.", "r.c." y "i.c." en la siguiente ecuación.

<math alttext="{displaystyle L(theta)=prod _{T_{i}in unc.}Pr(T=T_{i}mid theta)prod _{iin l.c.}Pr(TT_{i}mid theta)prod _{iin i.c.}Pr(T_{i,l}<TL()Silencio Silencio )=∏ ∏ Ti▪ ▪ unc.Pr()T=Ti▪ ▪ Silencio Silencio )∏ ∏ i▪ ▪ l.c.Pr()T.Ti▪ ▪ Silencio Silencio )∏ ∏ i▪ ▪ r.c.Pr()T■Ti▪ ▪ Silencio Silencio )∏ ∏ i▪ ▪ i.c.Pr()Ti,l.T.Ti,r▪ ▪ Silencio Silencio ).{displaystyle L(theta)=prod ¿Por qué? l.c.}Pr(T won_{i}mid theta)prod _{iin r.c.}Pr(T confíaT_{i}mid theta)prod _{iin i.c.}Pr(T_{i,l}traducidoT_{i,r}mid theta).}<img alt="{displaystyle L(theta)=prod _{T_{i}in unc.}Pr(T=T_{i}mid theta)prod _{iin l.c.}Pr(TT_{i}mid theta)prod _{iin i.c.}Pr(T_{i,l}<T

T_{i}

{displaystyle Pr(T=T_{i}mid theta)=f(T_{i}mid theta).}

T_{i}

<math alttext="{displaystyle Pr(TPr()T.Ti▪ ▪ Silencio Silencio )=F()Ti▪ ▪ Silencio Silencio )=1− − S()Ti▪ ▪ Silencio Silencio ).{displaystyle Pr(T won_{i}mid theta)=F(T_{i}mid theta)=1-S(T_{i}mid theta).}<img alt="{displaystyle Pr(T

T_{i}

T_{i}mid theta)=1-F(T_{i}mid theta)=S(T_{i}mid theta).}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">Pr()T■Ti▪ ▪ Silencio Silencio )=1− − F()Ti▪ ▪ Silencio Silencio )=S()Ti▪ ▪ Silencio Silencio ).{displaystyle Pr(T confianzaT_{i}mid theta)=1-F(T_{i}mid theta)=S(T_{i}mid theta).}T_{i}mid theta)=1-F(T_{i}mid theta)=S(T_{i}mid theta).}" aria-hidden="true" class="mwe-math-fallback-image-display" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/8bde6775c27b735bfc82355e8d4aede0e2829282" style="vertical-align: -0.838ex; width:42.298ex; height:2.843ex;"/>

T_{{i,r}}

T_{{i,l}}

<math alttext="{displaystyle Pr(T_{i,l}<TPr()Ti,l.T.Ti,r▪ ▪ Silencio Silencio )=S()Ti,l▪ ▪ Silencio Silencio )− − S()Ti,r▪ ▪ Silencio Silencio ).{displaystyle Pr(T_{i,l}traducidoT_{i,r}mid theta)=S(T_{i,l}mid theta)-S(T_{i,r}mid theta).}<img alt="{displaystyle Pr(T_{i,l}<T

T_{i}

Estimación no paramétrica

El estimador de Kaplan-Meier se puede utilizar para estimar la función de supervivencia. El estimador de Nelson-Aalen se puede utilizar para proporcionar una estimación no paramétrica de la función de tasa de riesgo acumulada.

Bondad de ajuste

La bondad de ajuste de los modelos finos de supervivencia se puede evaluar mediante reglas de puntuación.

Software informático para análisis de supervivencia

El libro de texto de Kleinbaum tiene ejemplos de análisis de supervivencia utilizando SAS, R y otros paquetes. Los libros de texto de Brostrom, Dalgaard y Tableman y Kim dé ejemplos de análisis de supervivencia usando R (o usando S, y que se ejecutan en R).

Distribuciones utilizadas en el análisis de supervivencia

Distribución exponencial
Distribución del vestíbulo
Distribución logística de los registros
Distribución Gamma
Distribución exponencial-logarítmica
Distribución gamma generalizada

Aplicaciones

Riesgo de crédito
False conviction rate of inmates sentenced to death
Tiempos de plomo para componentes metálicos en la industria aeroespacial
Predicadores de reincidencia criminal
Distribución de supervivencia de animales con etiquetas radiales
Muerte temporal a violenta de emperadores romanos
Intertrade tiempos de espera de acciones intercambiadas electrónicamente en una bolsa

Contenido relacionado

Más resultados...