Análisis de sensibilidad

Análisis de sensibilidad es el estudio de cómo la incertidumbre en la salida de un modelo o sistema matemático (numérico o de otro tipo) puede dividirse y asignarse a diferentes fuentes de incertidumbre en sus entradas. Una práctica relacionada es el análisis de incertidumbre, que se centra más en la cuantificación de la incertidumbre y su propagación; Idealmente, los análisis de incertidumbre y sensibilidad deberían realizarse en conjunto.

El proceso de recalcular los resultados bajo supuestos alternativos para determinar el impacto de una variable bajo el análisis de sensibilidad puede ser útil para una variedad de propósitos, que incluyen:

• Probando la robustez de los resultados de un modelo o sistema en presencia de incertidumbre.
• Mayor comprensión de las relaciones entre variables de entrada y salida en un sistema o modelo.
• La reducción de la incertidumbre, mediante la identificación de los insumos modelo que causan una incertidumbre significativa en la producción y, por lo tanto, debe ser el centro de atención para aumentar la robustez (tal vez mediante nuevas investigaciones).
• Búsqueda de errores en el modelo (encontrando relaciones inesperadas entre entradas y salidas).
• simplificación modelo – fijación de entrada modelo que no tiene efecto en la salida, o identificación y eliminación de partes redundantes de la estructura modelo.
• Mejorar la comunicación de los modelistas a los encargados de adoptar decisiones (por ejemplo, haciendo recomendaciones más creíbles, comprensibles, convincentes o persuasivas).
• Encontrar regiones en el espacio de factores de entrada para los cuales la salida del modelo es máxima o mínima o cumple algún criterio óptimo (ver optimización y filtrado Monte Carlo).
• En caso de calibrar modelos con gran número de parámetros, una prueba de sensibilidad primaria puede facilitar la etapa de calibración centrándose en los parámetros sensibles. No conocer la sensibilidad de los parámetros puede resultar en que el tiempo se gaste inútilmente en los no sensibles.
• Tratar de identificar conexiones importantes entre las observaciones, los insumos modelo y las predicciones o previsiones, lo que conduce al desarrollo de mejores modelos.

Descripción general

Un modelo matemático (por ejemplo en biología, cambio climático, economía o ingeniería) puede ser muy complejo y, como resultado, sus relaciones entre entradas y salidas pueden no entenderse bien. En tales casos, el modelo puede verse como una caja negra, es decir, la salida es una caja "opaca" función de sus entradas. Muy a menudo, algunos o todos los datos de entrada del modelo están sujetos a fuentes de incertidumbre, incluidos errores de medición, ausencia de información y una comprensión deficiente o parcial de las fuerzas y mecanismos impulsores. Esta incertidumbre impone un límite a nuestra confianza en la respuesta o resultado del modelo. Además, es posible que los modelos tengan que hacer frente a la variabilidad intrínseca natural del sistema (aleatoria), como la ocurrencia de eventos estocásticos.

En modelos que involucran muchas variables de entrada, el análisis de sensibilidad es un ingrediente esencial en la construcción del modelo y el aseguramiento de la calidad. Las agencias nacionales e internacionales involucradas en estudios de evaluación de impacto han incluido secciones dedicadas al análisis de sensibilidad en sus directrices. Algunos ejemplos son la Comisión Europea (véanse, por ejemplo, las directrices para la evaluación de impacto), la Oficina de Gestión y Presupuesto de la Casa Blanca, el Panel Intergubernamental sobre Cambio Climático y las directrices de modelización de la Agencia de Protección Ambiental de EE. UU.

Configuraciones, restricciones y cuestiones relacionadas

Configuraciones y restricciones

La elección del método de análisis de sensibilidad suele estar dictada por una serie de limitaciones o entornos del problema. Algunos de los más comunes son

• Gastos computacionales: El análisis de sensibilidad se realiza casi siempre ejecutando el modelo un número (posiblemente grande) de veces, es decir, un enfoque basado en muestreo. Esto puede ser un problema importante cuando,
  • Una sola ejecución del modelo lleva una cantidad significativa de tiempo (minutos, horas o más). Esto no es inusual con modelos muy complejos.
  • El modelo tiene un gran número de entradas inciertas. El análisis de sensibilidad es esencialmente la exploración del espacio de entrada multidimensional, que crece exponencialmente en tamaño con el número de entradas. Vea la maldición de la dimensionalidad.

El gasto computacional es un problema en muchos análisis prácticos de sensibilidad. Algunos métodos para reducir los gastos computacionales incluyen el uso de emuladores (para modelos grandes), y métodos de detección (para reducir la dimensionalidad del problema). Otro método es utilizar un método de análisis de sensibilidad basado en eventos para la selección variable para aplicaciones con restricciones temporales. Este es un método de selección variable de entrada (IVS) que reúne información sobre el rastro de los cambios en las entradas y salidas del sistema utilizando análisis de sensibilidad para producir una matriz de disparador/evento de entrada/salida que está diseñada para mapear las relaciones entre los datos de entrada como causas que desencadenan eventos y los datos de salida que describen los eventos reales. La relación causa-efecto entre las causas del cambio estatal es decir, las variables de entrada y los parámetros de salida del sistema de efecto determina qué conjunto de entradas tienen un impacto genuino en una salida dada. El método tiene una clara ventaja sobre el método de IVS analítico y computacional ya que trata de entender e interpretar el cambio de estado del sistema en el menor tiempo posible con una sobrecarga mínima computacional.

• Entradas relacionadas con los corsales: La mayoría de los métodos comunes de análisis de sensibilidad asumen la independencia entre los insumos modelo, pero a veces los insumos pueden estar fuertemente correlacionados. Este es todavía un campo inmaduro de investigación y todavía no se han establecido métodos definitivos.
• No linealidad: Algunos enfoques de análisis de sensibilidad, como los basados en la regresión lineal, pueden medir inexactamente la sensibilidad cuando la respuesta modelo no es lineal con respecto a sus insumos. En esos casos, las medidas basadas en las diferencias son más apropiadas.
• Múltiples salidas: Prácticamente todos los métodos de análisis de sensibilidad consideran una única salida de modelo univariate, pero muchos modelos producen un gran número de datos posiblemente espaciales o dependientes del tiempo. Tenga en cuenta que esto no excluye la posibilidad de realizar diferentes análisis de sensibilidad para cada salida de interés. Sin embargo, para los modelos en los que se correlacionan los productos, las medidas de sensibilidad pueden ser difíciles de interpretar.

Suposiciones versus inferencias

En el análisis de incertidumbre y sensibilidad existe un equilibrio crucial entre qué tan escrupuloso es un analista al explorar los supuestos de entrada y qué tan amplia puede ser la inferencia resultante. El econometrista Edward E. Leamer ilustra bien este punto:

He propuesto una forma de análisis de sensibilidad organizado que llamo "análisis de sensibilidad global" en el que se selecciona un barrio de suposiciones alternativas y se identifica el intervalo correspondiente de inferencias. Se considera que las conclusiones son robustas sólo si el vecindario de supuestos es lo suficientemente amplio como para ser creíble y el intervalo correspondiente de las inferencias es lo suficientemente estrecho como para ser útil.

Nota: El énfasis de Leamer está en la necesidad de 'credibilidad' en la selección de supuestos. La forma más fácil de invalidar un modelo es demostrar que es frágil con respecto a la incertidumbre de los supuestos o demostrar que sus supuestos no se han tomado "lo suficientemente amplios". Jerome R. Ravetz expresa el mismo concepto, para quien un mal modelado es cuando las incertidumbres en los insumos deben suprimirse para que los resultados no se vuelvan indeterminados.

Escollos y dificultades

Algunas dificultades comunes en el análisis de sensibilidad incluyen

• Demasiados modelos para analizar. El análisis se puede utilizar para reducir la dimensionalidad. Otra manera de abordar la maldición de la dimensionalidad es utilizar el muestreo basado en secuencias de baja discrepancia
• El modelo tarda mucho en correr. Los emuladores (incluyendo HDMR) pueden reducir el tiempo total acelerando el modelo o reduciendo el número de carreras de modelos necesarias.
• No hay suficiente información para construir distribuciones de probabilidad para los insumos. Las distribuciones de probabilidad se pueden construir a partir de la obtención de expertos, aunque incluso entonces puede ser difícil construir distribuciones con gran confianza. La subjetividad de las distribuciones o rangos de probabilidad afectará fuertemente el análisis de sensibilidad.
• El propósito no claro del análisis. Se aplican diferentes pruebas y medidas estadísticas al problema y se obtienen diferentes clasificaciones de factores. En cambio, la prueba debe ajustarse al propósito del análisis, por ejemplo, se utiliza el filtro Monte Carlo si se interesa en qué factores son los más responsables de generar valores altos/bajos de la salida.
• Se consideran demasiados productos modelo. Esto puede ser aceptable para la garantía de calidad de los submodelos, pero debe evitarse al presentar los resultados del análisis general.
• Sensibilidad parcial. Esto es cuando se realiza el análisis de sensibilidad en un submodelo a la vez. Este enfoque no es conservador, ya que podría pasar por alto las interacciones entre factores en diferentes submodels (error tipo II).

Métodos de análisis de sensibilidad

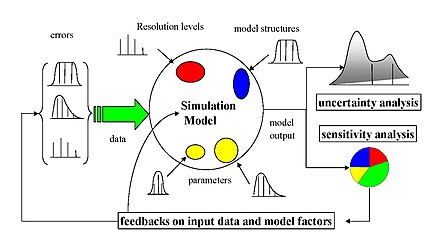
Existe una gran cantidad de enfoques para realizar un análisis de sensibilidad, muchos de los cuales se han desarrollado para abordar una o más de las limitaciones analizadas anteriormente. También se distinguen por el tipo de medida de sensibilidad, ya sea basada (por ejemplo) en descomposiciones de varianza, derivadas parciales o efectos elementales. Sin embargo, en general, la mayoría de los procedimientos se ajustan al siguiente esquema:

1. Cuantifique la incertidumbre en cada entrada (por ejemplo, rangos, distribuciones de probabilidad). Tenga en cuenta que esto puede ser difícil y existen muchos métodos para obtener distribuciones de incertidumbre de datos subjetivos.
2. Identificar la salida modelo a analizar (el objetivo de interés debe tener una relación directa con el problema abordado por el modelo).
3. Ejecute el modelo varias veces usando algún diseño de experimentos, dictado por el método de elección y la incertidumbre de entrada.
4. Utilizando los productos de modelo resultantes, calcula las medidas de sensibilidad de interés.

En algunos casos, este procedimiento se repetirá, por ejemplo, en problemas de alta dimensión donde el usuario tiene que descartar variables sin importancia antes de realizar un análisis de sensibilidad completo.

Los distintos tipos de "métodos básicos" (que se analizan a continuación) se distinguen por las diversas medidas de sensibilidad que se calculan. Estas categorías pueden de alguna manera superponerse. Se pueden ofrecer formas alternativas de obtener estas medidas, según las limitaciones del problema.

Uno a la vez (OAT)

Uno de los enfoques más simples y comunes es cambiar un factor a la vez (OAT) para ver qué efecto produce esto en la salida. La OAT habitualmente implica

• moviendo una variable de entrada, manteniendo a otros en sus valores de base (nominales), entonces,
• devolver la variable a su valor nominal, repitiendo para cada una de las otras entradas de la misma manera.

La sensibilidad puede entonces medirse monitoreando los cambios en la salida, p.e. mediante derivadas parciales o regresión lineal. Este parece un enfoque lógico ya que cualquier cambio observado en la salida se deberá inequívocamente a la única variable modificada. Además, al cambiar una variable a la vez, se pueden mantener todas las demás variables fijas en sus valores centrales o de referencia. Esto aumenta la comparabilidad de los resultados (todos los "efectos" se calculan con referencia al mismo punto central en el espacio) y minimiza las posibilidades de fallos del programa informático, más probables cuando se cambian varios factores de entrada simultáneamente. Los modeladores suelen preferir la OAT por razones prácticas. En caso de fallo del modelo bajo el análisis OAT, el modelador sabe inmediatamente cuál es el factor de entrada responsable del fallo.

Sin embargo, a pesar de su simplicidad, este enfoque no explora completamente el espacio de entrada, ya que no tiene en cuenta la variación simultánea de las variables de entrada. Esto significa que el enfoque OAT no puede detectar la presencia de interacciones entre variables de entrada y no es adecuado para modelos no lineales.

La proporción del espacio de entrada que sigue sin explotar con un enfoque OAT crece superexponencialmente con el número de insumos. Por ejemplo, un espacio de 3 parámetros que se explora uno a uno es equivalente a tomar puntos a lo largo de los ejes x, y y z de un cubo centrado en el origen. El casco convexo que une todos estos puntos es un octaedro que tiene un volumen sólo 1/6 del espacio total del parámetro. Más generalmente, el casco convexo de los ejes de un hiperrectángulo forma un hiperoctaedro que tiene una fracción de volumen ${displaystyle 1/n!}$. Con 5 entradas, el espacio explorado ya baja a menos del 1% del espacio total del parámetro. E incluso esto es una sobreestimación, ya que el volumen fuera del eje no está siendo realmente muestreado en absoluto. Compare esto al muestreo aleatorio del espacio, donde el casco convexo se acerca a todo el volumen a medida que se agregan más puntos. Mientras que la espacidad de OAT no es teóricamente una preocupación por los modelos lineales, la verdadera linearidad es rara en la naturaleza.

Métodos locales basados en derivados

Los métodos basados en derivadas locales implican tomar la derivada parcial de la salida Y con respecto a un factor de entrada X_{i<. /sub>:}

${displaystyle left forever{frac {partial Y}{partial ¿Por qué? {x}} {0}}}$

donde el subíndice x⁰ indica que la derivada se toma en algún punto fijo en el espacio de la entrada (de ahí el 'local' en el nombre de la clase). El modelado adjunto y la diferenciación automatizada son métodos de esta clase. Al igual que OAT, los métodos locales no intentan explorar completamente el espacio de entrada, ya que examinan pequeñas perturbaciones, generalmente una variable a la vez. Es posible seleccionar muestras similares a partir de sensibilidad basada en derivadas a través de redes neuronales y realizar una cuantificación de la incertidumbre.

Una de las ventajas de los métodos locales es que es posible crear una matriz que represente todas las sensibilidades de un sistema, proporcionando así una visión general que no se puede lograr con los métodos globales si hay una gran cantidad de variables de entrada y salida.

Análisis de regresión

El análisis de regresión, en el contexto del análisis de sensibilidad, implica ajustar una regresión lineal a la respuesta del modelo y utilizar coeficientes de regresión estandarizados como medidas directas de sensibilidad. Se requiere que la regresión sea lineal con respecto a los datos (es decir, un hiperplano, por lo tanto sin términos cuadráticos, etc., como regresores) porque de lo contrario es difícil interpretar los coeficientes estandarizados. Por tanto, este método es más adecuado cuando la respuesta del modelo es de hecho lineal; La linealidad se puede confirmar, por ejemplo, si el coeficiente de determinación es grande. Las ventajas del análisis de regresión son que es simple y tiene un bajo costo computacional.

Métodos basados en varianza

Los métodos basados en la varianza son una clase de enfoques probabilísticos que cuantifican las incertidumbres de entrada y salida como distribuciones de probabilidad y descomponen la varianza de la salida en partes atribuibles a variables de entrada y combinaciones de variables. Por lo tanto, la sensibilidad de la salida a una variable de entrada se mide por la cantidad de varianza en la salida causada por esa entrada. Estas pueden expresarse como expectativas condicionales, es decir, considerando un modelo Y = f(X) para X = {X₁, X ₂,... X_k}, una medida de sensibilidad del La iésima variable X_i se da como,

${displaystyle operatorname {Var} left(E_{textbf {X}_{sim i}}left(Ymid X_{i}right)}}$

donde "Var" y "E" denota los operadores de varianza y valor esperado respectivamente, y X_~i denota el conjunto de todas las variables de entrada excepto < i>X_i. Esta expresión esencialmente mide la contribución X_i sola a la incertidumbre (varianza) en Y (promediada sobre las variaciones en otras variables), y se conoce como índice de sensibilidad de primer orden o índice de efecto principal. Es importante destacar que no mide la incertidumbre causada por las interacciones con otras variables. Otra medida, conocida como índice de efecto total, proporciona la varianza total en Y causada por X_i y sus interacciones con cualquiera de las otras variables de entrada. Ambas cantidades normalmente se estandarizan dividiendo por Var(Y).

Los métodos basados en varianza permiten una exploración completa del espacio de entrada, teniendo en cuenta las interacciones y las respuestas no lineales. Por estas razones se utilizan ampliamente cuando es factible calcularlos. Normalmente, este cálculo implica el uso de métodos de Monte Carlo, pero dado que esto puede implicar miles de ejecuciones del modelo, se pueden usar otros métodos (como emuladores) para reducir el gasto computacional cuando sea necesario.

Análisis de variogramas de superficies de respuesta (VARS)

Una de las principales deficiencias de los métodos anteriores de análisis de sensibilidad es que ninguno de ellos considera la estructura ordenada espacialmente de la superficie de respuesta / salida del modelo Y=f()X) en el espacio del parámetro. Utilizando los conceptos de variogramas y covariogramas direccionales, el análisis de variogramas de superficies de respuesta (VARS) aborda esta debilidad mediante el reconocimiento de una estructura de correlación continua espacial a los valores de Y, y por lo tanto también a los valores de ${fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft} Y... #$.

Básicamente, cuanto mayor es la variabilidad, más heterogénea es la superficie de respuesta a lo largo de una dirección/parámetro particular, en una escala de perturbación específica. En consecuencia, en el marco VARS, los valores de los variogramas direccionales para una escala de perturbación determinada pueden considerarse como una ilustración integral de la información de sensibilidad, al vincular el análisis de variogramas con los conceptos de dirección y escala de perturbación. Como resultado, el marco VARS tiene en cuenta el hecho de que la sensibilidad es un concepto que depende de la escala y, por lo tanto, supera la cuestión de la escala de los métodos tradicionales de análisis de sensibilidad. Más importante aún, VARS es capaz de proporcionar estimaciones relativamente estables y estadísticamente sólidas de la sensibilidad de los parámetros con un costo computacional mucho menor que otras estrategias (aproximadamente dos órdenes de magnitud más eficientes). Cabe destacar que se ha demostrado que existe un vínculo teórico entre el marco VARS y los enfoques basados en varianza y derivados.

Métodos alternativos

Se han desarrollado varios métodos para superar algunas de las limitaciones analizadas anteriormente, que de otro modo harían inviable la estimación de medidas de sensibilidad (la mayoría de las veces debido a gastos computacionales). Generalmente, estos métodos se centran en calcular eficientemente medidas de sensibilidad basadas en la varianza.

Emuladores

Los emuladores (también conocidos como metamodelos, modelos sustitutos o superficies de respuesta) son enfoques de modelado de datos/aprendizaje automático que implican la construcción de una función matemática relativamente simple, conocida como emulador, que aproxima la entrada/ comportamiento de salida del propio modelo. En otras palabras, es el concepto de "modelar un modelo" (de ahí el nombre "metamodelo"). La idea es que, aunque los modelos informáticos pueden ser una serie muy compleja de ecuaciones cuya resolución puede llevar mucho tiempo, siempre pueden considerarse como una función de sus entradas Y = f(X). Al ejecutar el modelo en varios puntos del espacio de entrada, es posible adaptar un emulador mucho más simple η(X), tal que η(X) ≈ f(X) dentro de un margen de error aceptable. Luego, las medidas de sensibilidad se pueden calcular desde el emulador (ya sea con Monte Carlo o analíticamente), lo que tendrá un costo computacional adicional insignificante. Es importante destacar que el número de ejecuciones del modelo necesarias para ajustar el emulador puede ser órdenes de magnitud menor que el número de ejecuciones necesarias para estimar directamente las medidas de sensibilidad del modelo.

Claramente, el quid de un enfoque de emulador es encontrar un η (emulador) que sea una aproximación suficientemente cercana al modelo f. Esto requiere los siguientes pasos,

1. Muestra (correr) el modelo en varios puntos en su espacio de entrada. Esto requiere un diseño de muestra.
2. Seleccionar un tipo de emulador (función matemática) para usar.
3. "Training" el emulador utilizando los datos de la muestra del modelo – esto generalmente implica ajustar los parámetros del emulador hasta que el emulador mime el verdadero modelo tanto como sea posible.

El muestreo del modelo a menudo se puede realizar con secuencias de baja discrepancia, como la secuencia de Sobol, debido al matemático Ilya M. Sobol o el muestreo de hipercubo latino, aunque también se pueden usar diseños aleatorios, con pérdida de algo de eficiencia. La selección del tipo de emulador y el entrenamiento están intrínsecamente vinculados ya que el método de entrenamiento dependerá de la clase de emulador. Algunos tipos de emuladores que se han utilizado con éxito para el análisis de sensibilidad incluyen,

• Procesos gaussianos (también conocido como kriging), donde se supone que cualquier combinación de puntos de salida se distribuya como una distribución multivariada gaussiana. Recientemente, los procesos gaussianos "arbolados" se han utilizado para tratar con respuestas heteroscedasticas y discontinuas.
• Los bosques aleatorios, en los que se entrenan un gran número de árboles de decisión, y el resultado se promedia.
• Ampliación gradual, donde una sucesión de simples regresiones se utilizan para ponderar los puntos de datos para reducir secuencialmente el error.
• Expansiones polinomiales de caos, que utilizan polinomios ortogonales para aproximar la superficie de respuesta.
• Smoothing splines, normalmente utilizado en combinación con truncaciones HDMR (ver abajo).
• Discreta redes bayesianas, junto con modelos canónicos como modelos ruidosos. Los modelos ruidosos explotan información sobre la independencia condicional entre variables para reducir significativamente la dimensionalidad.

El uso de un emulador introduce un problema de aprendizaje automático, que puede resultar difícil si la respuesta del modelo es muy no lineal. En todos los casos, resulta útil comprobar la precisión del emulador, por ejemplo mediante validación cruzada.

Representaciones de modelos de alta dimensión (HDMR)

Una representación de modelo de alta dimensión (HDMR) (el término se debe a H. Rabitz) es esencialmente un enfoque de emulador, que implica descomponer la salida de la función en una combinación lineal de términos de entrada e interacciones de dimensionalidad creciente. El enfoque HDMR aprovecha el hecho de que el modelo normalmente puede aproximarse bien ignorando las interacciones de orden superior (segundo o tercer orden y superiores). Los términos de la serie truncada pueden entonces aproximarse, por ejemplo, mediante polinomios o splines (REFS) y la respuesta expresada como la suma de los principales efectos e interacciones hasta el orden de truncamiento. Desde esta perspectiva, los HDMR pueden verse como emuladores que descuidan las interacciones de alto orden; la ventaja es que pueden emular modelos con mayor dimensionalidad que los emuladores de orden completo.

Prueba de sensibilidad de amplitud de Fourier (FAST)

La prueba de sensibilidad de amplitud de Fourier (FAST) utiliza la serie de Fourier para representar una función multivariada (el modelo) en el dominio de la frecuencia, utilizando una única variable de frecuencia. Por lo tanto, las integrales necesarias para calcular los índices de sensibilidad se vuelven univariadas, lo que genera ahorros computacionales.

Otro

Métodos basados en el filtrado Monte Carlo.< Estos también se basan en muestreos y el objetivo aquí es identificar regiones en el espacio de los factores de entrada correspondientes a valores particulares (por ejemplo, altos o bajos) de la salida.

Aplicaciones

Se pueden encontrar ejemplos de análisis de sensibilidad en diversas áreas de aplicación, como:

• Environmental sciences
• Negocios
• Ciencias sociales
• Química
• Ingeniería
• Epidemiología
• Meta-análisis
• Toma de decisiones de múltiples criterios
• Toma de decisiones con carácter crítico
• Calibración modelo
• Cuantificación de la incertidumbre
• Teoría de caos
  • En la genética poblacional — Si una población se convertirá en caótica cuando reciba un período de esteticidad

Auditoría de sensibilidad

Puede suceder que un análisis de sensibilidad de un estudio basado en modelos tenga como objetivo respaldar una inferencia y certificar su solidez, en un contexto donde la inferencia alimenta una política o un proceso de toma de decisiones. En estos casos, el marco del análisis en sí, su contexto institucional y las motivaciones de su autor pueden convertirse en una cuestión de gran importancia, y un análisis de sensibilidad puro –con su énfasis en la incertidumbre paramétrica– puede considerarse insuficiente. El énfasis en el marco puede derivar, entre otras cosas, de la relevancia del estudio de políticas para diferentes grupos de interés que se caracterizan por diferentes normas y valores y, por lo tanto, por una historia diferente sobre "cuál es el problema" y, en consecuencia, por una historia diferente sobre "cuál es el problema". y, sobre todo, sobre "quién cuenta la historia". Muy a menudo, el marco incluye suposiciones más o menos implícitas, que pueden ser políticas (por ejemplo, qué grupo necesita ser protegido) hasta técnicas (por ejemplo, qué variable puede tratarse como una constante).

Para tener en cuenta estas preocupaciones, los instrumentos de SA se han ampliado para proporcionar una evaluación de todo el proceso de generación de conocimientos y modelos. Este enfoque se ha denominado “auditoría de sensibilidad”. Se inspira en NUSAP, un método utilizado para calificar el valor de la información cuantitativa con la generación de pedigríes. de números. La auditoría de sensibilidad ha sido especialmente diseñada para un contexto adversarial, donde no sólo la naturaleza de la evidencia, sino también el grado de certeza e incertidumbre asociada a la evidencia, será objeto de intereses partidistas. La auditoría de sensibilidad se recomienda en las directrices de la Comisión Europea para la evaluación de impacto, así como en el informe Science Advice for Policy by European Academies.

Conceptos relacionados

El análisis de sensibilidad está estrechamente relacionado con el análisis de incertidumbre; mientras que este último estudia la incertidumbre general en las conclusiones del estudio, el análisis de sensibilidad intenta identificar qué fuente de incertidumbre pesa más en las conclusiones del estudio.

La formulación de problemas en el análisis de sensibilidad también tiene grandes similitudes con el campo del diseño de experimentos. En un diseño de experimentos, se estudia el efecto de algún proceso o intervención (el "tratamiento") sobre algunos objetos (las "unidades experimentales"). En el análisis de sensibilidad se analiza el efecto de variar las entradas de un modelo matemático sobre la salida del modelo mismo. En ambas disciplinas uno se esfuerza por obtener información del sistema con un mínimo de experimentos físicos o numéricos.