Análisis de Fourier
En matemáticas, el análisis de Fourier () es el estudio de la forma en que las funciones generales pueden representarse o aproximarse mediante sumas de funciones trigonométricas más simples. El análisis de Fourier surgió del estudio de las series de Fourier y lleva el nombre de Joseph Fourier, quien demostró que representar una función como una suma de funciones trigonométricas simplifica enormemente el estudio de la transferencia de calor.
El tema del análisis de Fourier abarca un amplio espectro de las matemáticas. En las ciencias y la ingeniería, el proceso de descomposición de una función en componentes oscilatorios a menudo se denomina análisis de Fourier, mientras que la operación de reconstrucción de la función a partir de estas piezas se conoce como síntesis de Fourier. Por ejemplo, determinar qué frecuencias componentes están presentes en una nota musical implicaría calcular la transformada de Fourier de una nota musical muestreada. Luego, se podría volver a sintetizar el mismo sonido al incluir los componentes de frecuencia como se revela en el análisis de Fourier. En matemáticas, el término análisis de Fourier a menudo se refiere al estudio de ambas operaciones.
El proceso de descomposición en sí se llama transformación de Fourier. Su salida, la transformada de Fourier, a menudo recibe un nombre más específico, que depende del dominio y otras propiedades de la función que se transforma. Además, el concepto original del análisis de Fourier se ha ampliado con el tiempo para aplicarse a situaciones cada vez más abstractas y generales, y el campo general se conoce a menudo como análisis armónico. Cada transformada utilizada para el análisis (consulte la lista de transformadas relacionadas con Fourier) tiene una transformada inversa correspondiente que se puede utilizar para la síntesis.
Para usar el análisis de Fourier, los datos deben estar igualmente espaciados. Se han desarrollado diferentes enfoques para analizar datos espaciados de manera desigual, en particular los métodos de análisis espectral de mínimos cuadrados (LSSA) que utilizan un ajuste de mínimos cuadrados de sinusoides a muestras de datos, similar al análisis de Fourier. El análisis de Fourier, el método espectral más utilizado en la ciencia, generalmente aumenta el ruido de período largo en registros con intervalos prolongados; LSSA mitiga tales problemas.
Aplicaciones
El análisis de Fourier tiene muchas aplicaciones científicas: en física, ecuaciones diferenciales parciales, teoría de números, combinatoria, procesamiento de señales, procesamiento de imágenes digitales, teoría de probabilidad, estadística, análisis forense, fijación de precios de opciones, criptografía, análisis numérico, acústica, oceanografía, sonar, óptica, difracción, geometría, análisis de estructura de proteínas y otras áreas.
Esta amplia aplicabilidad se deriva de muchas propiedades útiles de las transformadas:
- Los transformados son operadores lineales y, con la normalización adecuada, también son unitarios (una propiedad conocida como teorema de Parseval o, más generalmente, como teorema de Plancherel, y más generalmente a través de la dualidad de Pontryagin).
- Las transformaciones son generalmente invertibles.
- Las funciones exponenciales son funciones eigen de diferenciación, lo que significa que esta representación transforma las ecuaciones diferenciales lineales con coeficientes constantes en las algebraicas ordinarias. Por lo tanto, el comportamiento de un sistema lineal de tiempo-invariante se puede analizar en cada frecuencia de forma independiente.
- Mediante el teorema de la convolución, Fourier transforma la complicada operación de la convolución en simple multiplicación, lo que significa que proporcionan una manera eficiente de calcular las operaciones basadas en la convolución, como el filtrado de señales, la multiplicación polinomio y multiplicando grandes números.
- La versión discreta de la transformación Fourier (ver abajo) se puede evaluar rápidamente en ordenadores usando algoritmos de transformación rápida Fourier (FFT).
En medicina forense, los espectrofotómetros infrarrojos de laboratorio utilizan el análisis de transformada de Fourier para medir las longitudes de onda de la luz a las que un material absorberá en el espectro infrarrojo. El método FT se utiliza para decodificar las señales medidas y registrar los datos de longitud de onda. Y mediante el uso de una computadora, estos cálculos de Fourier se llevan a cabo rápidamente, de modo que en cuestión de segundos, un instrumento FT-IR operado por computadora puede producir un patrón de absorción de infrarrojos comparable al de un instrumento de prisma.
La transformación de Fourier también es útil como representación compacta de una señal. Por ejemplo, la compresión JPEG utiliza una variante de la transformación de Fourier (transformada de coseno discreta) de pequeñas piezas cuadradas de una imagen digital. Los componentes de Fourier de cada cuadrado se redondean a una precisión aritmética más baja y los componentes débiles se eliminan por completo, de modo que los componentes restantes se pueden almacenar de forma muy compacta. En la reconstrucción de imágenes, cada cuadrado de la imagen se vuelve a ensamblar a partir de los componentes transformados de Fourier aproximados conservados, que luego se transforman inversamente para producir una aproximación de la imagen original.
En el procesamiento de señales, la transformada de Fourier a menudo toma una serie de tiempo o una función de tiempo continuo y la mapea en un espectro de frecuencia. Es decir, lleva una función del dominio del tiempo al dominio de la frecuencia; es una descomposición de una función en sinusoides de diferentes frecuencias; en el caso de una serie de Fourier o una transformada discreta de Fourier, las sinusoides son armónicos de la frecuencia fundamental de la función que se analiza.
Cuando una función s()t){displaystyle s(t)} es una función del tiempo y representa una señal física, la transformación tiene una interpretación estándar como el espectro de frecuencia de la señal. La magnitud de la función de valor complejo resultante S()f){displaystyle S(f)} a frecuencia f{displaystyle f} representa la amplitud de un componente de frecuencia cuya fase inicial es dada por el ángulo de S()f){displaystyle S(f)} (coordinaciones polares).
Las transformadas de Fourier no se limitan a funciones de tiempo y frecuencias temporales. Se pueden aplicar igualmente para analizar frecuencias espaciales y, de hecho, para casi cualquier dominio de función. Esto justifica su uso en ramas tan diversas como el procesamiento de imágenes, la conducción de calor y el control automático.
Al procesar señales, como audio, ondas de radio, ondas de luz, ondas sísmicas e incluso imágenes, el análisis de Fourier puede aislar los componentes de banda estrecha de una forma de onda compuesta, concentrándolos para detectarlos o eliminarlos más fácilmente. Una gran familia de técnicas de procesamiento de señales consiste en la transformación de Fourier de una señal, la manipulación de los datos transformados por Fourier de manera sencilla y la inversión de la transformación.
Algunos ejemplos incluyen:
- Equiparación de grabaciones de audio con una serie de filtros de bandapass;
- Recibimiento digital de radio sin circuito de superheterodina, como en un moderno teléfono celular o escáner de radio;
- Procesamiento de imágenes para eliminar artefactos periódicos o anisotrópicos como jaggies de vídeo interlazado, artefactos de rayas de la fotografía aérea de rayas, o patrones de onda de interferencia de radio frecuencia en una cámara digital;
- Correlación cruzada de imágenes similares para la alineación;
- Cristalografía de rayos X para reconstruir una estructura de cristal de su patrón de diffracción;
- Espectrometría de masa de resonancia ciclotron de Fourier-transform ion para determinar la masa de iones de la frecuencia de movimiento ciclotron en un campo magnético;
- Muchas otras formas de espectroscopia, incluyendo espectroscopias de resonancia magnética infrarroja y nuclear;
- Generación de espectrogramas de sonido utilizados para analizar sonidos;
- Sonar pasivo utilizado para clasificar objetivos basados en ruido de maquinaria.
Variantes del análisis de Fourier
(Continua) Transformada de Fourier
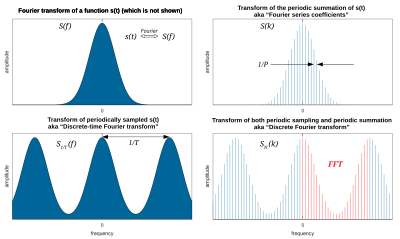
La mayoría de las veces, el término no calificado transformada de Fourier se refiere a la transformada de funciones de un argumento real continuo, y produce una función continua de frecuencia, conocida como distribución de frecuencia. Una función se transforma en otra y la operación es reversible. Cuando el dominio de la función de entrada (inicial) es el tiempo (t), y el dominio de la función de salida (final) es frecuencia ordinaria, la transformada de la función s(t) en la frecuencia f está dada por el número complejo:
- S()f)=∫ ∫ − − JUEGO JUEGO JUEGO JUEGO s()t)⋅ ⋅ e− − i2π π ftdt.{displaystyle S(f)=int _{-infty }s(t)cdot e^{-i2pi ft},dt.}
Evaluar esta cantidad para todos los valores de f produce la función dominio de frecuencia. Entonces s(t) se puede representar como una recombinación de exponenciales complejos de todas las frecuencias posibles:
- s()t)=∫ ∫ − − JUEGO JUEGO JUEGO JUEGO S()f)⋅ ⋅ ei2π π ftdf,{displaystyle s(t)=int _{-infty } {infty }S(f)cdot e^{i2pi.
que es la fórmula de la transformada inversa. El número complejo, S(f), transmite tanto la amplitud como la fase de la frecuencia f.
Consulte la transformada de Fourier para obtener mucha más información, que incluye:
- convenciones para la normalización de la amplitud y escalada de frecuencias/unidades
- transforma propiedades
- transformaciones tabuladas de funciones específicas
- una extensión/generalización para funciones de múltiples dimensiones, como imágenes.
Serie de Fourier
La transformada de Fourier de una función periódica, sP(t), con punto P, se convierte en una función peine de Dirac, modulada por una secuencia de coeficientes complejos:
- S[k]=1P∫ ∫ PsP()t)⋅ ⋅ e− − i2π π kPtdt,k▪ ▪ Z,{displaystyle S[k]={frac {1}{P}int} ¿Por qué? {fnMicroc {k}{P}t},dt,quad kin mathbb {Z} (donde) ∫P es la integral sobre cualquier intervalo de longitud P).
La transformada inversa, conocida como serie de Fourier, es una representación de sP (t) en términos de una suma de un número potencialmente infinito de sinusoides relacionados armónicamente o funciones exponenciales complejas, cada una con una amplitud y una fase especificadas por uno de los coeficientes:
- sP()t)=F− − 1{}.. k=− − JUEGO JUEGO +JUEGO JUEGO S[k]δ δ ()f− − kP)}=.. k=− − JUEGO JUEGO JUEGO JUEGO S[k]⋅ ⋅ ei2π π kPt.{displaystyle s_{P}(t)\\\\cHFF}}m1}left{sum _{k=-infty }{+infty }S[k],delta left(f-{frac {k}{}right)right}\=\fnMicrosoft Sans Serif} sum _{k=-infty {fnMicroc No.
Cualquier sP(t) puede expresarse como una suma periódica de otra función, s(t):
- sP()t)≜ ≜ .. m=− − JUEGO JUEGO JUEGO JUEGO s()t− − mP),{displaystyle s_{P}(t),triangleq ,sum _{m=-infty }{infty }s(t-mP),}
y los coeficientes son proporcionales a muestras de S(f) a intervalos discretos de 1/P:
- S[k]=1P⋅ ⋅ S()kP).{displaystyle S={frac {1}cdot Sleft {k}{P}right).}
Tenga en cuenta que cualquier s(t) cuya transformada tenga los mismos valores de muestra discretos se puede usar en el periódico suma. Una condición suficiente para recuperar s(t) (y por lo tanto S (f)) de solo estas muestras (es decir, de la serie de Fourier) es que la parte distinta de cero de s (t) limitarse a un intervalo de duración conocido P, que es el dominio de frecuencia dual del teorema de muestreo de Nyquist-Shannon.
Consulte la serie de Fourier para obtener más información, incluido el desarrollo histórico.
Transformada de Fourier en tiempo discreto (DTFT)
La DTFT es el dual matemático de la serie de Fourier en el dominio del tiempo. Por lo tanto, una suma periódica convergente en el dominio de la frecuencia se puede representar mediante una serie de Fourier, cuyos coeficientes son muestras de una función de tiempo continua relacionada:
- S1T()f)≜ ≜ .. k=− − JUEGO JUEGO JUEGO JUEGO S()f− − kT)↑ ↑ .. n=− − JUEGO JUEGO JUEGO JUEGO s[n]⋅ ⋅ e− − i2π π fnT⏞ ⏞ Serie Fourier (DTFT)⏟ ⏟ Poisson summation formula=F{}.. n=− − JUEGO JUEGO JUEGO JUEGO s[n]δ δ ()t− − nT)},{displaystyle S_{frac {1} {f)\trianglequnderbrace {sum _{k=-infty }{infty }Sleft(f-{frac {k}{T}right)equiv overbrace {sum _{n=-infty }{infty }s[n]cdot e^{-i2pi fnT} ^{text{f} Serie Fourier (DTFT)}}} ¿Por qué?
que se conoce como DTFT. Por lo tanto, el DTFT de la secuencia s[n] es también el Fourier transform de la función peine de Dirac modulada.
Los coeficientes de la serie de Fourier (y la transformada inversa) están definidos por:
- s[n]≜ ≜ T∫ ∫ 1TS1T()f)⋅ ⋅ ei2π π fnTdf=T∫ ∫ − − JUEGO JUEGO JUEGO JUEGO S()f)⋅ ⋅ ei2π π fnTdf⏟ ⏟ ≜ ≜ s()nT).{displaystyle s[n] triangleq Tint _{frac {1} {T}S_{frac} {1} {T}(f)cdot e^{i2pi fnT},df=Tunderbrace {int _{-infty }S(f)cdot e^{i2pi fnT},df} _{triangleq ,s(nT)}. }
El parámetro T corresponde al intervalo de muestreo, y esta serie de Fourier ahora se puede reconocer como una forma de la fórmula de suma de Poisson. Así tenemos el importante resultado de que cuando una secuencia de datos discretos, s[n], es proporcional a las muestras de un función continua subyacente, s(t), se puede observar una suma periódica de la transformada continua de Fourier, S(f). Tenga en cuenta que cualquier s(t) con los mismos valores de muestra discretos produce la misma DTFT Pero bajo ciertas condiciones idealizadas uno puede teóricamente recuperar S(f) y s(t) exactamente. Una condición suficiente para una recuperación perfecta es que la parte distinta de cero de S(f) se limite a una frecuencia conocida intervalo de ancho 1/T. Cuando ese intervalo es [−1/2T, 1/2T] , la fórmula de reconstrucción aplicable es la fórmula de interpolación de Whittaker-Shannon. Esta es una piedra angular en la base del procesamiento de señales digitales.
Otra razón para estar interesado en S1/T(f) es que a menudo proporciona información sobre la cantidad de alias causado por el proceso de muestreo.
Las aplicaciones de la DTFT no se limitan a funciones muestreadas. Consulte Transformada de Fourier en tiempo discreto para obtener más información sobre este y otros temas, incluidos:
- unidades de frecuencia normalizadas
- ventana (secuencias de longitud final)
- transforma propiedades
- transformaciones tabuladas de funciones específicas
Transformada discreta de Fourier (DFT)
Similar a una serie Fourier, el DTFT de una secuencia periódica, sN[n]{displaystyle S_{N}[n], con período N{displaystyle N}, se convierte en una función de peine Dirac, modulada por una secuencia de coeficientes complejos (ver DTFT § Datos periódicos):
- S[k]=.. nsN[n]⋅ ⋅ e− − i2π π kNn,k▪ ▪ Z,{displaystyle S[k]=sum ¿Qué? {fnK}n}n},quad kin mathbb {Z} (donde) .n es la suma sobre cualquier secuencia de longitud N).
La secuencia S[k] es lo que habitualmente se conoce como DFT de un ciclo de sN. También es N-periódico, por lo que nunca es necesario calcular más de N coeficientes. La transformada inversa, también conocida como serie discreta de Fourier, viene dada por:
- sN[n]=1N.. kS[k]⋅ ⋅ ei2π π nNk,{displaystyle S_{N}[n]={frac {1}{N}sum _{k}S[k]cdot e^{i2pi {fnMicroc {N} k},} Donde .k es la suma sobre cualquier secuencia de longitud N.
Cuando sN[n] se expresa como una suma periódica de otra función:
- sN[n]≜ ≜ .. m=− − JUEGO JUEGO JUEGO JUEGO s[n− − mN],{displaystyle s_{N}[n],triangleqsum _{m=-infty }{infty }s[n-mN],} y s[n]≜ ≜ s()nT),{displaystyle s[n],triangleq ,s(nT),}
los coeficientes son proporcionales a muestras de S1/T (f) a intervalos discretos de 1/P = 1/NT:
- S[k]=1T⋅ ⋅ S1T()kP).{displaystyle S[k]={frac {1} {T}cdot S_{frac {1}left({frac {k}}right).}
Por el contrario, cuando se quiere calcular un número arbitrario (N) de muestras discretas de un ciclo de una DTFT continua, S1/T(f) , se puede hacer calculando la DFT relativamente simple de sN [n], como se define anteriormente. En la mayoría de los casos, N se elige igual a la longitud de la parte distinta de cero de s[n]. El aumento de N, conocido como zero-padding o interpolación, da como resultado muestras más próximas entre sí de un ciclo de S1/T(f). La disminución de N provoca superposición (adición) en el dominio del tiempo (análogo al aliasing), que corresponde a la destrucción en el dominio de la frecuencia. (ver Transformada de Fourier de tiempo discreto § L=N×I) En la mayoría de los casos de interés práctico, s[n] secuencia representa una secuencia más larga que se truncó mediante la aplicación de una función de ventana de longitud finita o una matriz de filtro FIR.
La DFT se puede calcular mediante un algoritmo de transformada rápida de Fourier (FFT), lo que la convierte en una transformación práctica e importante en las computadoras.
Consulte Transformada discreta de Fourier para obtener mucha más información, que incluye:
- transforma propiedades
- Aplicaciones
- transformaciones tabuladas de funciones específicas
Resumen
Para funciones periódicas, tanto la transformada de Fourier como la DTFT comprenden solo un conjunto discreto de componentes de frecuencia (serie de Fourier), y las transformadas divergen en esas frecuencias. Una práctica común (no discutida anteriormente) es manejar esa divergencia a través de las funciones delta de Dirac y peine de Dirac. Pero la misma información espectral se puede discernir de un solo ciclo de la función periódica, ya que todos los demás ciclos son idénticos. De manera similar, las funciones de duración finita se pueden representar como una serie de Fourier, sin pérdida real de información, excepto que la periodicidad de la transformada inversa es un mero artefacto.
Es común en la práctica que la duración de s(•) se limite al período, P o N. Pero estas fórmulas no exigen esa condición.
| Frecuencia continua | Frecuencias discretas | |
|---|---|---|
| Transformación | S()f)≜ ≜ ∫ ∫ − − JUEGO JUEGO JUEGO JUEGO s()t)⋅ ⋅ e− − i2π π ftdt{displaystyle S(f),triangleqint _{-infty }{infty }s(t)cdot e^{-i2pi ft},dt} | 1P⋅ ⋅ S()kP)⏞ ⏞ S[k]≜ ≜ 1P∫ ∫ − − JUEGO JUEGO JUEGO JUEGO s()t)⋅ ⋅ e− − i2π π kPtdt↑ ↑ 1P∫ ∫ PsP()t)⋅ ⋅ e− − i2π π kPtdt{displaystyle overbrace {frac {1}{}cdot Sleft({frac {k}right)} {cdot Sleft},triangleq ,{frac}}}}}ccH00} {1}{infty }s(t)cdot e^{-i2pi) {fnMicroc {k}{}t},dtequiv {frac {1}{P}int} ¿Por qué? {fnMicroc {K} {} t},dt} |
| Inverso | s()t)=∫ ∫ − − JUEGO JUEGO JUEGO JUEGO S()f)⋅ ⋅ ei2π π ftdf{displaystyle s(t)=int _{-infty } {infty }S(f)cdot e^{i2pi ft},df} | sP()t)=.. k=− − JUEGO JUEGO JUEGO JUEGO S[k]⋅ ⋅ ei2π π kPt⏟ ⏟ Poisson summation formula (Fourier series){displaystyle underbrace {s_{P}(t)=sum _{k=-infty }^{infty }S[k]cdot e^{i2pi {fnMicroc {} {} {} t}} ##{text{Poisson summation formula (Fourier series)},} |
| Frecuencia continua | Frecuencias discretas | |
|---|---|---|
| Transformación | 1TS1T()f)≜ ≜ .. n=− − JUEGO JUEGO JUEGO JUEGO s()nT)⋅ ⋅ e− − i2π π fnT⏟ ⏟ Poisson summation formula (DTFT){displaystyle underbrace {frac {1} {T}S_{frac} {1}{T}(f),triangleq ,sum _{n=-infty }{infty }s(nT)cdot e^{-i2pi fnT} _{text{text{Poisson summation formula (DTFT)}}}}}}}}} | 1TS1T()kNT)⏞ ⏞ S[k]≜ ≜ .. n=− − JUEGO JUEGO JUEGO JUEGO s()nT)⋅ ⋅ e− − i2π π knN↑ ↑ .. nsP()nT)⋅ ⋅ e− − i2π π knN⏟ ⏟ DFT{displaystyle {begin{aligned}overbrace {frac}{}S_{frac} {1}{T}}left({frac {k}{NT}right)} ^{S[k]}, recurtriangleq ,sum _{n=-infty } {infty }s(nT)cdot e^{-i2pi {fnMicroc {kn} {fn}\\\fn}\\fn}\\\\\fn}\\\\\fn}}\\\\\\fn}\\\\\\\\\fn}\\\\\\\fn}}}}}}}\\\\\\\\\\\\\\\\fn}\\\\\\\\\\\\\\\\\\\\fn}\\\\\\\\fn}}}}}}}}\\\\\\\\\\\\\\\\\ underbrace {sum _{n}s_{P}(nT)cdot e^{-i2pi {fnMicroc {fn} {fn} {fnK}}fnK}fnK}}} {fn} {fn} {fnK}}}} {fnK}}}} {fn}}} {fnf}}}}} {\\\fnfnK\f}}}}}\\\\fnfn\\\\fnfnfnfn\fnfn\fn\fnfnfn\fnfnfn\\\\\fn\\\fnfnfnfnfnfnfn\\fn\fnfn\fn\\fnfnfn\\fn\\fnfn}fnfn |
| Inverso | s()nT)=T∫ ∫ 1T1TS1T()f)⋅ ⋅ ei2π π fnTdf{displaystyle s(nT)=Tint _{frac {1}{fn} {fnMicroc} {1} {T}S_{frac} {1} {T}(f)cdot e^{i2pi. .. n=− − JUEGO JUEGO JUEGO JUEGO s()nT)⋅ ⋅ δ δ ()t− − nT)=∫ ∫ − − JUEGO JUEGO JUEGO JUEGO 1TS1T()f)⋅ ⋅ ei2π π ftdf⏟ ⏟ inverso Fourier transform{displaystyle sum _{n=-infty }{infty }s(nT)cdot delta (t-nT)=underbrace {int _{-infty. {1} {T}f} S_{frac {1} {T}(f)cdot e^{i2pi ¿Por qué? Fourier transform},} | sP()nT)=1N.. kS[k]⋅ ⋅ ei2π π knN⏞ ⏞ inverso DFT=1P.. kS1T()kP)⋅ ⋅ ei2π π knN{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicroc {fn}}}sum _{k}S[k]cdot e^{i2pi {fnMicroc {kn}{N}}} ^{text{inverse ¿Qué? ¿Qué? {1} {T}left({frac} {k}{i2pi)cdot {fnMicroc {kn} {fn}end{aligned}} |
Propiedades de simetría
Cuando las partes real e imaginaria de una función compleja se descomponen en sus partes pares e impares, hay cuatro componentes, indicados a continuación con los subíndices RE, RO, IE e IO. Y hay un mapeo uno a uno entre los cuatro componentes de una función de tiempo compleja y los cuatro componentes de su transformada de frecuencia compleja:
- Dominio de tiempos=sRE+sRO+isIE+isIO⏟ ⏟ ⇕F⇕F⇕F⇕F⇕FDominio de frecuenciaS=SRE+iSIO⏞ ⏞ +iSIE+SRO{displaystyle {begin{array}{rccccccccccccccccc}{text{Time} {fnMicrosoft Sans} {fnMicrosoft Sans}}} {fnMicrosoft Sans_}}} {f}}}} {text{\f}}} {\fnMicrosoft}}} {fnK}} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft} {f} {f} {fnMicrosoft}
A partir de esto, varias relaciones son evidentes, por ejemplo:
- La transformación de una función de valor real (sRE + sRO) es la función simétrica incluso SRE + i SIO. Por el contrario, una transformación incluso simétrica implica un dominio de tiempo real.
- La transformación de una función de valor imaginario (i sIE + i sIO) es la función simétrica extraña SRO + i SIE, y el contrario es cierto.
- La transformación de una función incluso simétrica (sRE + i sIO) es la función de valor real SRE + SRO, y el contrario es cierto.
- La transformación de una función simétrica extraña (sRO + i sIE) es la función de valor imaginario i SIE + i SIO, y el contrario es cierto.
Historia
Una forma temprana de series armónicas se remonta a las antiguas matemáticas babilónicas, donde se usaban para calcular efemérides (tablas de posiciones astronómicas).
Los conceptos griegos clásicos de deferente y epiciclo en el sistema ptolemaico de astronomía estaban relacionados con las series de Fourier (ver Deferente y epiciclo § Formalismo matemático).
En tiempos modernos, Alexis Clairaut utilizó variantes de la transformada discreta de Fourier en 1754 para calcular una órbita, que ha sido descrita como la primera fórmula para la DFT, y en 1759 por Joseph Louis Lagrange, al calcular los coeficientes de una serie trigonométrica para una cuerda vibrante. Técnicamente, el trabajo de Clairaut era una serie de solo coseno (una forma de transformada de coseno discreta), mientras que el trabajo de Lagrange era una serie de solo seno (una forma de transformada de seno discreta); Gauss utilizó en 1805 una verdadera DFT coseno+seno para la interpolación trigonométrica de las órbitas de los asteroides. Tanto Euler como Lagrange discretizaron el problema de la cuerda vibrante, usando lo que hoy se llamaría muestras.
Un desarrollo moderno temprano hacia el análisis de Fourier fue el artículo de 1770 Réflexions sur la résolution algébrique des équations de Lagrange, que en el método de los resolventes de Lagrange usaba una descomposición compleja de Fourier para estudiar la solución de una ecuación cúbica: Lagrange transformó las raíces x1, x2, x 3 en los resolventes:
- r1=x1+x2+x3r2=x1+Especificaciones Especificaciones x2+Especificaciones Especificaciones 2x3r3=x1+Especificaciones Especificaciones 2x2+Especificaciones Especificaciones x3{displaystyle {begin{aligned}r_{1} limit=x_{1}+x_{2}+x_{3}\r_{2} x_{2}+zeta ^{2}x_{3}r_{3} ^{2}x_{2}+zeta ¿Qué?
donde ζ es una raíz cúbica de la unidad, que es la DFT de orden 3.
Varios autores, en particular Jean le Rond d'Alembert y Carl Friedrich Gauss, utilizaron series trigonométricas para estudiar la ecuación del calor, pero el avance revolucionario fue el artículo de 1807 Mémoire sur la propagation de la chaleur dans les corps solides de Joseph Fourier, cuya idea fundamental fue modelar todas las funciones mediante series trigonométricas, introduciendo la serie de Fourier.
Los historiadores están divididos en cuanto a cuánto darle crédito a Lagrange y a otros por el desarrollo de la teoría de Fourier: Daniel Bernoulli y Leonhard Euler habían introducido representaciones trigonométricas de funciones, y Lagrange había dado la solución de la serie de Fourier a la ecuación de onda, por lo que Fourier&# La contribución de 39 fue principalmente la audaz afirmación de que una función arbitraria podría representarse mediante una serie de Fourier.
El desarrollo posterior del campo se conoce como análisis armónico y también es una instancia temprana de la teoría de la representación.
El primer algoritmo de transformada rápida de Fourier (FFT) para la DFT fue descubierto alrededor de 1805 por Carl Friedrich Gauss al interpolar mediciones de la órbita de los asteroides Juno y Palas, aunque ese algoritmo de FFT en particular se atribuye más a menudo a sus modernos redescubridores Cooley y Tukey.
Transformadas tiempo-frecuencia
En términos de procesamiento de señales, una función (de tiempo) es una representación de una señal con una resolución de tiempo perfecta, pero sin información de frecuencia, mientras que la transformada de Fourier tiene una resolución de frecuencia perfecta. i>, pero no hay información de tiempo.
Como alternativas a la transformada de Fourier, en el análisis de tiempo-frecuencia, se utilizan transformadas de tiempo-frecuencia para representar señales en una forma que tiene alguna información de tiempo y alguna información de frecuencia; según el principio de incertidumbre, existe una compensación entre estas. Estas pueden ser generalizaciones de la transformada de Fourier, como la transformada de Fourier de tiempo corto, la transformada de Gabor o la transformada fraccionaria de Fourier (FRFT), o pueden usar diferentes funciones para representar señales, como en las transformadas wavelet y chirplet, con el análogo de wavelet de la transformada de Fourier (continua) siendo la transformada wavelet continua.
Transformadas de Fourier en grupos topológicos abelianos localmente compactos arbitrarios
Las variantes de Fourier también se pueden generalizar a transformadas de Fourier en grupos topológicos abelianos localmente compactos arbitrarios, que se estudian en el análisis armónico; allí, la transformada de Fourier lleva funciones en un grupo a funciones en el grupo dual. Este tratamiento también permite una formulación general del teorema de convolución, que relaciona las transformadas de Fourier y las convoluciones. Consulte también la dualidad de Pontryagin para conocer los fundamentos generalizados de la transformada de Fourier.
Más específico, el análisis de Fourier se puede realizar en clases laterales, incluso en clases laterales discretas.
Contenido relacionado
Combinador de punto fijo
Ciclo de trabajo
Número imaginario






![{displaystyle S[k]={frac {1}{P}}int _{P}s_{P}(t)cdot e^{-i2pi {frac {k}{P}}t},dt,quad kin mathbb {Z}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb7ea8c18081286c018bf5f7b8bb2c6f6ef45dd2)
![{displaystyle s_{P}(t) = {mathcal {F}}^{-1}left{sum _{k=-infty }^{+infty }S[k],delta left(f-{frac {k}{P}}right)right} = sum _{k=-infty }^{infty }S[k]cdot e^{i2pi {frac {k}{P}}t}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df07111464812a477d010681fb580dc1bf9bf93e)

![{displaystyle S[k]={frac {1}{P}}cdot Sleft({frac {k}{P}}right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/639522ac155d3a2aa8c2fcf1a47a69a699f0a0c2)
![{displaystyle S_{frac {1}{T}}(f) triangleq underbrace {sum _{k=-infty }^{infty }Sleft(f-{frac {k}{T}}right)equiv overbrace {sum _{n=-infty }^{infty }s[n]cdot e^{-i2pi fnT}} ^{text{Fourier series (DTFT)}}} _{text{Poisson summation formula}}={mathcal {F}}left{sum _{n=-infty }^{infty }s[n] delta (t-nT)right},,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f86c6a552be1eff44e868c611cf83788342397b7)
![{displaystyle s[n] triangleq Tint _{frac {1}{T}}S_{frac {1}{T}}(f)cdot e^{i2pi fnT},df=Tunderbrace {int _{-infty }^{infty }S(f)cdot e^{i2pi fnT},df} _{triangleq ,s(nT)}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4c2d37f7c8c2bdd52a8c6abe82bf25132e9555c)
![{displaystyle s_{N}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f85cdcca0edd9c7455b760f3ff1658815c74b66d)

![{displaystyle S[k]=sum _{n}s_{N}[n]cdot e^{-i2pi {frac {k}{N}}n},quad kin mathbb {Z}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60c12c67656c17b5bd0c8d003690043d763a979b)
![{displaystyle s_{N}[n]={frac {1}{N}}sum _{k}S[k]cdot e^{i2pi {frac {n}{N}}k},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dae0587546b45cd55f8a4ff36b0719431bdd4b84)
![{displaystyle s_{N}[n],triangleq ,sum _{m=-infty }^{infty }s[n-mN],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f208f4b9fa9ddb80c2b18ea10d5591bc906a005e)
![{displaystyle s[n],triangleq ,s(nT),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba13f1170ce74f79ba81423a048ec9e277d645be)
![{displaystyle S[k]={frac {1}{T}}cdot S_{frac {1}{T}}left({frac {k}{P}}right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b066a286d6fbdb43d343c332be7008015fb3ca5)

![{displaystyle overbrace {{frac {1}{P}}cdot Sleft({frac {k}{P}}right)} ^{S[k]},triangleq ,{frac {1}{P}}int _{-infty }^{infty }s(t)cdot e^{-i2pi {frac {k}{P}}t},dtequiv {frac {1}{P}}int _{P}s_{P}(t)cdot e^{-i2pi {frac {k}{P}}t},dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a88fe2f74f78af1dbf97555d07401b3417f8ba2)

![{displaystyle underbrace {s_{P}(t)=sum _{k=-infty }^{infty }S[k]cdot e^{i2pi {frac {k}{P}}t}} _{text{Poisson summation formula (Fourier series)}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b34e92026554e0a81498ff0726f6729c490d3cd8)

![{displaystyle {begin{aligned}overbrace {{frac {1}{T}}S_{frac {1}{T}}left({frac {k}{NT}}right)} ^{S[k]},&triangleq ,sum _{n=-infty }^{infty }s(nT)cdot e^{-i2pi {frac {kn}{N}}}\&equiv underbrace {sum _{n}s_{P}(nT)cdot e^{-i2pi {frac {kn}{N}}}} _{text{DFT}},end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e3df9f42f79c763316edb0a0fb6cce8a8aae438)


![{displaystyle {begin{aligned}s_{P}(nT)&=overbrace {{frac {1}{N}}sum _{k}S[k]cdot e^{i2pi {frac {kn}{N}}}} ^{text{inverse DFT}}\&={tfrac {1}{P}}sum _{k}S_{frac {1}{T}}left({frac {k}{P}}right)cdot e^{i2pi {frac {kn}{N}}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f9a8d8e15b5d0fc77417d8ba48c026141fc1d19)

