Análisis de covarianza

El Análisis de covarianza (ANCOVA) es un modelo lineal general que combina ANOVA y regresión. ANCOVA evalúa si las medias de una variable dependiente (DV) son iguales en todos los niveles de una o más variables independientes categóricas y en una o más variables continuas. Por ejemplo, las variables categóricas podrían describir el tratamiento y las variables continuas podrían ser covariables o variables molestas; o viceversa. Matemáticamente, ANCOVA descompone la varianza en el DV en varianza explicada por los CV, varianza explicada por el IV categórico y varianza residual. Intuitivamente, se puede considerar que ANCOVA es un "ajustador" de las variables. el DV por el grupo de los CV.

El modelo ANCOVA supone una relación lineal entre la respuesta (DV) y la covariable (CV):

Sí.ij=μ μ +τ τ i+B()xij− − x̄ ̄ )+ε ε ij.{displaystyle Y... +tau _{i}+mathrm {B} (x_{ij}-{overline {x})+epsilon _{ij}

En esta ecuación, el DV, Sí.ij{displaystyle y_{ij}} es la observación jth bajo el grupo categórico ith; el CV, xij{displaystyle x_{ij}} es jt observación del covariado bajo el igrupo. Variables en el modelo que se derivan de los datos observados son μ μ {displaystyle mu } (el gran medio) y x̄ ̄ {displaystyle {overline {x}}} (el medio global para covariar x{displaystyle x}). Las variables a instalar son τ τ i{displaystyle tau _{i} (el efecto del ide la categoría IV), B{displaystyle B} (la pendiente de la línea) y ε ε ij{displaystyle epsilon _{ij} (el término de error no observado asociado para el ja la observación it grupo).

Bajo esta especificación, los efectos categóricos del tratamiento suman a cero ().. iaτ τ i=0).{displaystyle left(sum _{i}{a}tau _{i}=0right). } Los supuestos estándar del modelo de regresión lineal también se supone que se sostienen, como se describe a continuación.

Usos

Aumentar potencia

ANCOVA se puede utilizar para aumentar el poder estadístico (la probabilidad de que se encuentre una diferencia significativa entre grupos cuando existe) al reducir la varianza del error dentro del grupo. Para entender esto es necesario entender la prueba utilizada para evaluar las diferencias entre grupos, la prueba F. La prueba F se calcula dividiendo la varianza explicada entre grupos (por ejemplo, diferencias en la recuperación médica) por la varianza no explicada dentro de los grupos. De este modo,

F=MSbetweenMSwithin{displaystyle F={frac {MS_{between} {MS_{in}} {MS_{within}}} {MS_{within}} {MS_{within}}} {MS_{within}}} {} {} {} {} {}} {} {} {} {}} {}}} {}} {}}}}}}}}} {}}}} {}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {} {}}}}}} {}}}}}}}} {}}}}}}}}}}}} {}}}}}}}}}}}}}}} {}} {}}}}} {}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {

Si este valor es mayor que un valor crítico, concluimos que existe una diferencia significativa entre los grupos. La varianza inexplicable incluye la varianza del error (por ejemplo, diferencias individuales), así como la influencia de otros factores. Por tanto, la influencia de los CV se agrupa en el denominador. Cuando controlamos el efecto de los CV en el DV, lo eliminamos del denominador haciendo que F sea más grande, aumentando así nuestro poder para encontrar un efecto significativo, si es que existe alguno.

Ajustar diferencias preexistentes

Otro uso de ANCOVA es ajustar las diferencias preexistentes en grupos no equivalentes (intactos). Esta controvertida aplicación tiene como objetivo corregir las diferencias de grupo iniciales (antes de la asignación de grupo) que existen en DV entre varios grupos intactos. En esta situación, los participantes no pueden ser iguales mediante asignación aleatoria, por lo que los CV se utilizan para ajustar las puntuaciones y hacer que los participantes sean más similares que sin el CV. Sin embargo, incluso con el uso de covariables, no existen técnicas estadísticas que puedan equiparar grupos desiguales. Además, el CV puede estar tan íntimamente relacionado con la categoría IV que eliminar la variación en el DV asociado con el CV eliminaría una variación considerable en el DV, haciendo que los resultados carezcan de significado.

Suposiciones

Existen varios supuestos clave que subyacen al uso de ANCOVA y afectan la interpretación de los resultados. Se mantienen los supuestos estándar de regresión lineal; Además, asumimos que la pendiente de la covariable es igual en todos los grupos de tratamiento (homogeneidad de las pendientes de regresión).

Supuesto 1: linealidad de la regresión

La relación de regresión entre la variable dependiente y las variables concomitantes debe ser lineal.

Supuesto 2: homogeneidad de las variaciones de error

El error es una variable aleatoria con media condicional cero y varianzas iguales para diferentes clases de tratamiento y observaciones.

Supuesto 3: independencia de los términos de error

Los errores no están correlacionados. Es decir, la matriz de covarianza del error es diagonal.

Supuesto 4: normalidad de los términos de error

Los residuos (títulos de terrorismo) deben distribuirse normalmente ε ε ij{displaystyle epsilon _{ij} ~ N()0,σ σ 2){displaystyle N(0,sigma ^{2}.

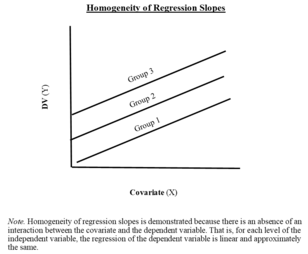
Supuesto 5: homogeneidad de las pendientes de regresión

Las pendientes de las diferentes líneas de regresión deben ser equivalentes, es decir, las líneas de regresión deben ser paralelas entre los grupos.

La quinta cuestión, relativa a la homogeneidad de las diferentes pendientes de regresión de tratamiento, es particularmente importante a la hora de evaluar la idoneidad del modelo ANCOVA. También tenga en cuenta que sólo necesitamos que los términos de error estén distribuidos normalmente. De hecho, tanto la variable independiente como las variables concomitantes no tendrán una distribución normal en la mayoría de los casos.

Realización de un ANCOVA

Prueba de multicolinealidad

Si un CV está altamente relacionado con otro CV (con una correlación de 0,5 o más), entonces no ajustará el DV por encima del otro CV. Uno u otro debería eliminarse ya que son estadísticamente redundantes.

Pruebe la homogeneidad del supuesto de varianza

Tested by Levene 's test of equality of error variances. This is most important after adjustments have been made, but if you have it before adjustment you are likely to have it afterwards.

Pruebe la homogeneidad del supuesto de pendientes de regresión

Para ver si el CV interactúa significativamente con el IV categórico, ejecute un modelo ANCOVA que incluya el término de interacción IV y CVxIV. Si la interacción CVxIV es significativa, no se debe realizar ANCOVA. En cambio, Green & Salkind sugiere evaluar las diferencias grupales en el DV en niveles particulares del CV. Considere también utilizar un análisis de regresión moderado, tratando el CV y su interacción como otro IV. Alternativamente, se podrían utilizar análisis de mediación para determinar si el CV explica el efecto del IV en el DV.

Ejecutar análisis ANCOVA

Si la interacción CV×IV no es significativa, vuelva a ejecutar el ANCOVA sin el término de interacción CV×IV. En este análisis, debe utilizar las medias ajustadas y el MSerror ajustado. Las medias ajustadas (también denominadas medias de mínimos cuadrados, medias LS, medias marginales estimadas o EMM) se refieren a las medias del grupo después de controlar la influencia del CV en el DV.

Follow-up analysis

Si hubo un efecto principal significativo, significa que hay una diferencia significativa entre los niveles de una categoría IV, ignorando todos los demás factores. Para encontrar exactamente qué niveles son significativamente diferentes entre sí, se pueden utilizar las mismas pruebas de seguimiento que para el ANOVA. Si hay dos o más IV, puede haber una interacción significativa, lo que significa que el efecto de un IV en el DV cambia dependiendo del nivel de otro factor. Se pueden investigar los efectos principales simples utilizando los mismos métodos que en un ANOVA factorial.

Consideraciones de potencia

Si bien la inclusión de una covariable en un ANOVA generalmente aumenta el poder estadístico al tener en cuenta parte de la varianza en la variable dependiente y, por lo tanto, aumenta la proporción de varianza explicada por las variables independientes, agregar una covariable en ANOVA también reduce los grados de libertad. En consecuencia, agregar una covariable que represente muy poca varianza en la variable dependiente podría en realidad reducir el poder.