Amplificador de retroalimentación negativa
Un amplificador de retroalimentación negativa (o amplificador de retroalimentación) es un amplificador electrónico que resta una fracción de su salida de su entrada, de modo que la retroalimentación negativa se opone a la señal original. La retroalimentación negativa aplicada puede mejorar su rendimiento (ganancia de estabilidad, linealidad, respuesta de frecuencia, respuesta de paso) y reduce la sensibilidad a las variaciones de parámetros debido a la fabricación o el entorno. Debido a estas ventajas, muchos amplificadores y sistemas de control usan retroalimentación negativa.
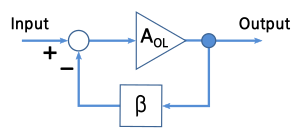
Un amplificador de retroalimentación negativa idealizado, como se muestra en el diagrama, es un sistema de tres elementos (consulte la Figura 1):
- an amplificador con ganancia AOL,
- a Red de información β, que siente la señal de salida y posiblemente la transforma de alguna manera (por ejemplo atenuando o filtrando),
- un circuito que actúa como un subtractor (el círculo de la figura), que combina la entrada y la salida transformada.
Resumen
Fundamentalmente, todos los dispositivos electrónicos que proporcionan ganancia de potencia (por ejemplo, tubos de vacío, transistores bipolares, transistores MOS) no son lineales. La retroalimentación negativa cambia la ganancia por una mayor linealidad (reduciendo la distorsión) y puede brindar otros beneficios. Si no se diseñan correctamente, los amplificadores con retroalimentación negativa pueden, en algunas circunstancias, volverse inestables debido a que la retroalimentación se vuelve positiva, lo que genera un comportamiento no deseado, como la oscilación. El criterio de estabilidad de Nyquist desarrollado por Harry Nyquist de Bell Laboratories se usa para estudiar la estabilidad de los amplificadores de retroalimentación.
Los amplificadores de retroalimentación comparten estas propiedades:
Ventajas:
- Puede aumentar o disminuir la impedancia de entrada (dependiendo del tipo de retroalimentación).
- Puede aumentar o disminuir la impedancia de salida (dependiendo del tipo de retroalimentación).
- Reduce la distorsión total si se aplica suficientemente (aumenta la linearidad).
- Aumenta el ancho de banda.
- Desensibiliza la ganancia a las variaciones de componentes.
- Puede controlar la respuesta paso del amplificador.
Contras:
- Puede llevar a la inestabilidad si no se diseña cuidadosamente.
- Disminuciones de ganancia amplificador.
- Impedancias de entrada y salida de un amplificador de retroalimentación negativo (amplificador de cierre cerrado) se vuelven sensibles a la ganancia de un amplificador sin retroalimentación (amplificador de apertura) - que expone estas impedancias a variaciones en la ganancia abierta, por ejemplo, debido a variaciones de parámetro o no linealidad de la ganancia abierta.
- Cambia la composición de la distorsión (aumento de audibilidad) si se aplica insuficientemente.
Historia
Paul Voigt patentó un amplificador de retroalimentación negativa en enero de 1924, aunque su teoría carecía de detalles. Harold Stephen Black inventó de forma independiente el amplificador de retroalimentación negativa mientras era pasajero en el ferry Lackawanna (desde la terminal de Hoboken a Manhattan) de camino al trabajo en Bell Laboratories (ubicado en Manhattan en lugar de Nueva Jersey en 1927) el 2 de agosto de 1927. (Patente de EE. UU. 2.102.671, emitida en 1937). Black estaba trabajando para reducir la distorsión en los amplificadores repetidores utilizados para la transmisión telefónica. En un espacio en blanco en su copia de The New York Times, registró el diagrama que se encuentra en la Figura 1 y las ecuaciones derivadas a continuación. El 8 de agosto de 1928, Black presentó su invento a la Oficina de Patentes de los Estados Unidos, que tardó más de 9 años en emitir la patente. Black escribió más tarde: "Una de las razones de la demora fue que el concepto era tan contrario a las creencias establecidas que la Oficina de Patentes inicialmente no creyó que funcionaría".
Comentarios clásicos
Usando el modelo de dos bloques unilaterales, simplemente se derivan varias consecuencias de la retroalimentación.
Reducción de ganancia
Abajo, la ganancia de voltaje del amplificador con retroalimentación, la ganancia de bucle cerrado AFB, se deriva en términos de la ganancia del amplificador sin retroalimentación, la ganancia de bucle abierto AOL y el factor de retroalimentación β, que gobierna cómo gran parte de la señal de salida se aplica a la entrada (ver Figura 1). La ganancia de lazo abierto AOL en general puede ser una función tanto de la frecuencia como del voltaje; el parámetro de retroalimentación β está determinado por la red de retroalimentación que está conectada alrededor del amplificador. Para un amplificador operacional, se pueden usar dos resistencias que forman un divisor de voltaje para que la red de retroalimentación establezca β entre 0 y 1. Esta red se puede modificar usando elementos reactivos como capacitores o inductores para (a) proporcionar una ganancia de bucle cerrado dependiente de la frecuencia como en circuitos de ecualización/control de tono o (b) construir osciladores. La ganancia del amplificador con retroalimentación se obtiene a continuación en el caso de un amplificador de voltaje con retroalimentación de voltaje.
Sin retroalimentación, el voltaje de entrada V′in se aplica directamente a la entrada del amplificador. El voltaje de salida correspondiente es
- VFuera.=AOL⋅ ⋅ Vdentro..{displaystyle V_{out}=A_{text{OL}cdot V'.
Supongamos ahora que un bucle de retroalimentación atenuante aplica una fracción β β ⋅ ⋅ VFuera.{displaystyle beta cdot V_{text{out}} de la salida a una de las entradas del subtractor para que se reste del voltaje de entrada del circuito Vdentro aplicado a la otra entrada de subtractor. El resultado de la resta aplicada a la entrada de amplificador es
- Vdentro.=Vdentro− − β β ⋅ ⋅ VFuera..{displaystyle V'_{text{in}=V_{in}-beta cdot V_{text{out}}
Sustituyendo V′in en la primera expresión,
- VFuera.=AOL()Vdentro− − β β ⋅ ⋅ VFuera.).{displaystyle V_{text{out}=A_{text{OL}(V_{text{in}}-beta cdot V_{text{out}). }
Reorganización:
- VFuera.()1+β β ⋅ ⋅ AOL)=Vdentro⋅ ⋅ AOL.{displaystyle V_{text{out}}(1+beta cdot A_{text{OL}}=V_{text{in}}cdot A_{text{OL}}
Entonces la ganancia del amplificador con retroalimentación, llamada ganancia de bucle cerrado, AFB viene dada por
- AFB=VFuera.Vdentro=AOL1+β β ⋅ ⋅ AOL.{displaystyle A_{text{FB}={frac {fnK} {fnK}} {fnK}}} {fnK}} {f}}}} {fn}} {fn}}}}} {fn}} {fn}}}} {fn}}}}}}} {f}}} {\fnKf}}}}}}}}}}}}}}}}}}} {\\f}}}}}}}}}} {\\\\\\fn\\\fn\fn}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}\\\\\\\\\\\fn}}\\\\\\\\\\\fnfnfnfn {A_{text{OL}}{1+betacdot A_{text{OL}}}}
Si AOL ≫ 1, entonces AFB ≈ 1 / β, y la amplificación efectiva (o ganancia de bucle cerrado) AFB se establece mediante la constante de retroalimentación β y, por lo tanto, lo establece la red de retroalimentación, generalmente una red reproducible simple, lo que hace que la linealización y la estabilización de la características de amplificación sencillas. Si hay condiciones en las que β AOL = −1, el amplificador tiene una amplificación infinita: se ha convertido en un oscilador y el sistema es inestable. Las características de estabilidad del producto de retroalimentación de ganancia β AOL a menudo se muestran e investigan en un gráfico de Nyquist (un gráfico polar del cambio de fase/ganancia como función paramétrica de la frecuencia).). Una técnica más simple, pero menos general, utiliza diagramas de Bode.
La combinación L = −β AOL aparece comúnmente en el análisis de retroalimentación y se denomina ganancia de bucle. La combinación (1 + β AOL) también aparece comúnmente y recibe varios nombres como el factor de desensibilidad, diferencia de retorno, o factor de mejora.
Resumen de términos
- Ganancia abierta = AOL{displaystyle A_{text{OL}}
- Ganancia de cierre cerrado = AOL1+β β ⋅ ⋅ AOL{displaystyle {frac {f}}{1+betacdot A_{text{OL}}}}}}}}}}
- Factor de retroalimentación = β β {displaystyle beta }
- Ganancia de ruido = 1/β β {displaystyle 1/beta}
- Ganancia de lazo = − − β β ⋅ ⋅ AOL{displaystyle -beta cdot A_{text{OL}}
- Factor de desensibilidad = 1+β β ⋅ ⋅ AOL{displaystyle 1+betacdot A_{text{OL}}
Extensión de ancho de banda
La retroalimentación se puede utilizar para ampliar el ancho de banda de un amplificador a costa de reducir la ganancia del amplificador. La Figura 2 muestra tal comparación. La figura se entiende de la siguiente manera. Sin retroalimentación, la llamada ganancia de bucle abierto en este ejemplo tiene una respuesta de frecuencia constante de tiempo único dada por
- AOL()f)=A01+jf/fC,{displaystyle A_{text{OL}(f)={frac {A_{0}{1+jf/f_{text{C}}}} {f}} {f}} {f}} {f}}}}} {f}}}}}} {f}}}}} {f}}}}}} {f}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {
donde fC es la frecuencia de corte o esquina del amplificador: en este ejemplo fC = 104 Hz, y la ganancia a frecuencia cero A0 = 105 V/V. La figura muestra que la ganancia es plana hasta la frecuencia de esquina y luego cae. Cuando hay realimentación, la llamada ganancia de bucle cerrado, como se muestra en la fórmula de la sección anterior, se convierte en
- AFB()f)=AOL1+β β AOL=A0/()1+jf/fC)1+β β A0/()1+jf/fC)=A01+jf/fC+β β A0=A0()1+β β A0)()1+jf()1+β β A0)fC).{displaystyle {begin{aligned}A_{text{FB}(f) {A_{text{OL}}{1+beta ¿Qué? {A_{0}/(1+jf/f_{text{C}}{1+beta A_{0}/(1+jf/f_{text{C}}}\ {A_{0}{1+jf/f_{text{C}+beta ¿Qué? {A_{0}{(1+beta A_{0})left(1+j{frac {f}{(1+beta ¿Qué?
La última expresión muestra que el amplificador de retroalimentación todavía tiene un comportamiento de constante de tiempo único, pero la frecuencia de esquina ahora aumenta por el factor de mejora (1 + β A0), y la ganancia a frecuencia cero se ha reducido exactamente en el mismo factor. Este comportamiento se denomina intercambio entre ganancia y ancho de banda. En la Figura 2, (1 + β A0) = 103, entonces AFB(0) = 105 / 103 = 100 V/V, y fC aumenta a 104 × 103 = 107 Hz.
Polos múltiples
Cuando la ganancia de bucle cerrado tiene varios polos, en lugar del polo único del ejemplo anterior, la retroalimentación puede generar polos complejos (partes reales e imaginarias). En un caso de dos polos, el resultado es un pico en la respuesta de frecuencia del amplificador de retroalimentación cerca de su frecuencia de esquina y oscilación y sobreimpulso en su respuesta de paso. En el caso de más de dos polos, el amplificador de retroalimentación puede volverse inestable y oscilar. Consulte la discusión sobre el margen de ganancia y el margen de fase. Para una discusión completa, ver Sansen.
Análisis de flujo de señales
Una idealización principal detrás de la formulación de la Introducción es la división de la red en dos bloques autónomos (es decir, con sus propias funciones de transferencia determinadas individualmente), un ejemplo simple de lo que a menudo se denomina 'partición de circuito', que se refiere en este caso a la división en un bloque de amplificación directa y un bloque de retroalimentación. En amplificadores prácticos, el flujo de información no es unidireccional como se muestra aquí. Con frecuencia, estos bloques se toman como redes de dos puertos para permitir la inclusión de la transferencia de información bilateral. Sin embargo, convertir un amplificador en esta forma no es una tarea trivial, especialmente cuando la retroalimentación involucrada no es global (es decir, directamente de la salida a la entrada) sino local. (es decir, retroalimentación dentro de la red, involucrando nodos que no coinciden con terminales de entrada y/o salida).
En estos casos más generales, el amplificador se analiza más directamente sin dividirlo en bloques como los del diagrama, utilizando en su lugar algún análisis basado en el análisis de flujo de señal, como el método de relación de retorno o el modelo de ganancia asintótica. Al comentar sobre el enfoque de flujo de señales, Choma dice:
- "En contraste con el diagrama de bloques y enfoques de dos puertos para el problema de análisis de redes de retroalimentación, los métodos de flujo de señales no exigen a priori suposiciones sobre las propiedades unilaterales o bilaterales del bucle abierto y los subcircuitos de retroalimentación. Moreover, they are not predicated on mutually independent open loop and feedback subcircuit transfer functions, and they do not require that feedback be implemented only globally. De hecho, las técnicas de flujo de señales ni siquiera requieren la identificación explícita del bucle abierto y los subcircuitos de retroalimentación. El flujo de señales elimina así los detrimentos omnipresentes de los análisis convencionales de redes de retroalimentación, pero además, resulta ser computacionalmente eficiente también".
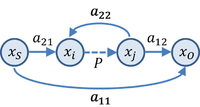
Siguiendo esta sugerencia, en la figura se muestra un gráfico de flujo de señal para un amplificador de retroalimentación negativa, que sigue el patrón de uno de D'Amico et al.. Siguiendo a estos autores, la notación es la siguiente:
- "Variables xS, xO representan las señales de entrada y salida, además, otras dos variables genéricas, xi, xj unidos a través del parámetro control (o crítico) P se muestran explícitamente. Parámetros aij son las ramas de peso. Variables xi, xj y el parámetro de control, P, modelar un generador controlado, o la relación entre tensión y corriente a través de dos nodos del circuito.
- El término a11 es la función de transferencia entre la entrada y la salida [después] establecer el parámetro de control, P, a cero; término a12 es la función de transferencia entre la salida y la variable controlada xj [después de] establecer la fuente de entrada, xS, a cero; término a21 representa la función de transferencia entre la variable fuente y la variable interna, xi cuando la variable controlada xj se establece a cero (es decir, cuando el parámetro de control, P se fija en cero); mandato a22 da la relación entre el parámetro de control de variables internas independientes y controladas, P y variable de entrada, xS, a cero."
Usando este gráfico, estos autores derivan la expresión de ganancia generalizada en términos del parámetro de control P que define la relación de fuente controlada xj = Pxi:
- xO=a11xS+a12xj,{displaystyle x_{text{O}=a_{11}x_{text{S}+a_{12}x_{j}}
- xi=a21xS+a22xj,{displaystyle x_{i}=a_{21}x_{text{S}+a_{22}x_{j}}
- xj=Pxi.{displaystyle x_{j}=Px_{i}
Combinando estos resultados, la ganancia viene dada por
- xOxS=a11+a12a21P1− − Pa22.{displaystyle {frac {x_{O}}{x_{text{S}}=a_{11}+{frac}} {f}}} {f}} {f}} {f}}} {f}}}} {f}}}}}}}}}}f} {a_{12}a_{21} {1-Pa_{22}}}
Para emplear esta fórmula, uno tiene que identificar una fuente controlada crítica para el circuito amplificador particular en cuestión. Por ejemplo, P podría ser el parámetro de control de una de las fuentes controladas en una red de dos puertos, como se muestra para un caso particular en D'Amico et al. Como ejemplo diferente, si tomamos a12 = a21 = 1, P = A, a22 = –β (retroalimentación negativa) y a11 = 0 (sin feedforward), recuperamos el resultado simple con dos bloques unidireccionales.
Análisis de retroalimentación en dos puertos
Aunque, como se mencionó en la sección Análisis de flujo de señal, algún tipo de análisis de flujo de señal es la forma más general de tratar el amplificador de retroalimentación negativa, la representación como dos puertos es el enfoque que se presenta con mayor frecuencia en los libros de texto y se presenta aquí. Conserva una partición de circuito de dos bloques del amplificador, pero permite que los bloques sean bilaterales. Algunos inconvenientes de este método se describen al final.
Los amplificadores electrónicos usan corriente o voltaje como entrada y salida, por lo que son posibles cuatro tipos de amplificadores (cualquiera de las dos entradas posibles con cualquiera de las dos salidas posibles). Ver clasificación de amplificadores. El objetivo del amplificador de retroalimentación puede ser cualquiera de los cuatro tipos de amplificador y no es necesariamente el mismo tipo que el amplificador de bucle abierto, que a su vez puede ser cualquiera de estos tipos. Entonces, por ejemplo, se puede configurar un amplificador operacional (amplificador de voltaje) para hacer un amplificador de corriente en su lugar.
Se pueden implementar amplificadores de retroalimentación negativa de cualquier tipo mediante combinaciones de redes de dos puertos. Hay cuatro tipos de red de dos puertos, y el tipo de amplificador deseado dicta la elección de dos puertos y la selección de una de las cuatro topologías de conexión diferentes que se muestran en el diagrama. Estas conexiones generalmente se denominan conexiones en serie o en derivación (paralelo). En el diagrama, la columna de la izquierda muestra las entradas de derivación; la columna de la derecha muestra las entradas en serie. La fila superior muestra las salidas en serie; la fila inferior muestra las salidas de derivación. Las diversas combinaciones de conexiones y dos puertos se enumeran en la siguiente tabla.
| Tipo de amplificador de retroalimentación | Input connection | Conexión de salida | Opinión ideal | Reacción de dos puertos |
|---|---|---|---|---|
| Corriente | Shunt | Serie | CCCS | g-parametro |
| Transresistencia | Shunt | Shunt | CCVS | y parámetro |
| Transconductancia | Serie | Serie | VCCS | z-parametro |
| Voltaje | Serie | Shunt | VCVS | h-parametro |
Por ejemplo, para un amplificador de retroalimentación de corriente, la corriente de la salida se muestrea para la retroalimentación y se combina con la corriente en la entrada. Por lo tanto, la retroalimentación idealmente se realiza usando una fuente de corriente controlada por corriente (CCCS) (de salida), y su realización imperfecta usando una red de dos puertos también debe incorporar un CCCS, es decir, la elección adecuada para la red de retroalimentación es una g- parámetro de dos puertos. Aquí se presenta el método de dos puertos utilizado en la mayoría de los libros de texto, utilizando el circuito tratado en el artículo sobre el modelo de ganancia asintótica.
La figura 3 muestra un amplificador de dos transistores con una resistencia de retroalimentación Rf. El objetivo es analizar este circuito para encontrar tres elementos: la ganancia, la impedancia de salida mirando al amplificador desde la carga y la impedancia de entrada mirando al amplificador desde la fuente.
Reemplazo de la red de retroalimentación por una de dos puertos
El primer paso es reemplazar la red de retroalimentación por una de dos puertos. ¿Qué componentes entran en los dos puertos?
En el lado de entrada de los dos puertos tenemos Rf. Si el voltaje en el lado derecho de Rf cambia, cambia la corriente en Rf que se resta de la corriente que ingresa a la base del transistor de entrada. Es decir, el lado de entrada de los dos puertos es una fuente de corriente dependiente controlada por el voltaje en la parte superior de la resistencia R2.
Se podría decir que la segunda etapa del amplificador es solo un seguidor de voltaje, que transmite el voltaje en el colector del transistor de entrada a la parte superior de R2. Es decir, la señal de salida monitoreada es realmente el voltaje en el colector del transistor de entrada. Esa opinión es legítima, pero luego la etapa del seguidor de voltaje se convierte en parte de la red de retroalimentación. Eso hace que el análisis de la retroalimentación sea más complicado.
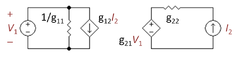
Una visión alternativa es que el voltaje en la parte superior de R2 lo establece la corriente del emisor del transistor de salida. Esa vista conduce a una red de retroalimentación completamente pasiva compuesta por R2 y Rf. La variable que controla la retroalimentación es la corriente del emisor, por lo que la retroalimentación es una fuente de corriente controlada por corriente (CCCS). Buscamos a través de las cuatro redes de dos puertos disponibles y encontramos que la única con un CCCS es la de dos puertos con parámetros g, que se muestra en la Figura 4. La siguiente tarea es seleccionar los parámetros g para que los dos puertos de la Figura 4 es eléctricamente equivalente a la sección L formada por R2 y Rf. Esa selección es un procedimiento algebraico que se realiza de la manera más simple observando dos casos individuales: el caso con V1 = 0, lo que hace que el VCVS esté en el lado derecho de los dos puerto un cortocircuito; y el caso con I2 = 0. lo que hace que el CCCS del lado izquierdo sea un circuito abierto. El álgebra en estos dos casos es simple, mucho más fácil que resolver todas las variables a la vez. La elección de los parámetros g que hacen que el dos puertos y la sección en L se comporten de la misma manera se muestran en la siguiente tabla.
| g11 | g12 | g21 | g22 |
|---|---|---|---|
| 1Rf+R2{displaystyle {frac}{mathrm {f} } | − − R2R2+Rf{displaystyle -{frac {R_{2} {R_{2}+R_{mathrm {f}}}} {}}}}} {R_{}}}}}}}} {R_}}} {}}} {}}}} {}}}}}}}} {R_}}}}}}}} {}}}}}} {R_}}}}}}} {}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} | R2R2+Rf{displaystyle {frac {R_{2}{R_{2}+R_{mathrm {f}}}}}} | R2SilencioSilencioRf{displaystyle ¿Qué? |
Circuito de pequeña señal
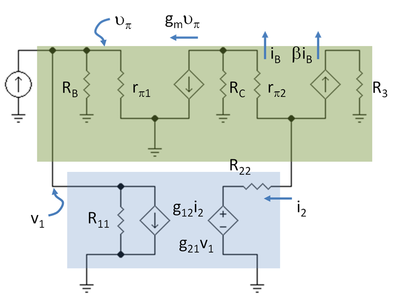
El siguiente paso es dibujar el esquema de pequeña señal para el amplificador con los dos puertos en su lugar usando el modelo híbrido-pi para los transistores. La Figura 5 muestra el esquema con notación R3 = RC2 || RL y R11 = 1 / g11, R22 = g22.
Ganancia de bucle abierto cargada
La figura 3 indica el nodo de salida, pero no la elección de la variable de salida. Una opción útil es la salida de corriente de cortocircuito del amplificador (que conduce a la ganancia de corriente de cortocircuito). Debido a que esta variable lleva simplemente a cualquiera de las otras opciones (por ejemplo, voltaje de carga o corriente de carga), la ganancia de corriente de cortocircuito se encuentra a continuación.
Primero se encuentra la ganancia de bucle abierto cargada. La retroalimentación se desactiva configurando g12 = g21 = 0. La idea es encontrar cuánto la ganancia del amplificador cambia debido a las resistencias en la red de retroalimentación por sí mismas, con la retroalimentación apagada. Este cálculo es bastante fácil porque R11, RB y rπ1 todos están en paralelo y v1 = vπ. Sea R1 = R11 || RB || rπ1. Además, i2 = −(β+1) iB. El resultado de la ganancia de corriente de bucle abierto AOL es:
- AOL=β β iBiS=gmRC()β β β β +1)()R1R22+rπ π 2+RCβ β +1).{displaystyle A_{mathrm}={frac {beta} i_{mathrm {B} }{i_{mathrm {S} }=g_{m}R_{mathrm {C}left({beta }{beta +1}derecha)left({frac {R_{1} {R_{22}+{frac} {fnh}+R_{mhm} Bueno...
Ganancia con comentarios
En el enfoque clásico de la retroalimentación, el feedforward representado por el VCVS (es decir, g21 v1) se desprecia. Eso hace que el circuito de la Figura 5 se asemeje al diagrama de bloques de la Figura 1, y la ganancia con retroalimentación es entonces:
- AFB=AOL1+β β FBAOL{displaystyle A_{mathrm {fnK} {fnMicroc {fnMicrosoft}{1+{beta} }_{mathrm {FB}A_{mathrm {OL}}}
- AFB=AOL1+R2R2+RfAOL,{displaystyle A_{mathrm {FB}={frac {mathrm} {fnMicrosoft} {fnMicrosoft}} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft}} {fnMicrosoft}} {f}} {fnMicroc {fnMicroc} {fnMicroc} {f}}}} {f}}}}}}}}}f}}}}}}}}}f}f}}}f}f}f} {f}f}f}f}f}f}f}f}f}f}f}f}f}\fnMicrocf}fnf}fn\\fnfnf}f}f}f}fnMicroc {fnMicroc {f}\f}f}f}}}f}fn }{1+{frac {R_{2} {R_{2}} {f}} {f}}} {f}}}}}}}}}}} {f}}}}}}}} {f}} {}}}}}}}}}}}}}}}}}}}}}} {}} {}}}}}}}}}}}}}}}}}} {}}} {}}}}}}}}}}}} {}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}
- AFB=AOL1+β β FBAOL{displaystyle A_{mathrm {fnK} {fnMicroc {fnMicrosoft}{1+{beta} }_{mathrm {FB}A_{mathrm {OL}}}
donde el factor de retroalimentación βFB = −g12. Se introduce la notación βFB para el factor de retroalimentación para distinguirlo del transistor β.
Resistencias de entrada y salida
La retroalimentación se usa para hacer coincidir mejor las fuentes de señal con sus cargas. Por ejemplo, una conexión directa de una fuente de voltaje a una carga resistiva puede resultar en una pérdida de señal debido a la división de voltaje, pero intercalar un amplificador de retroalimentación negativa puede aumentar la carga aparente vista por la fuente y reducir la impedancia aparente del controlador vista por la carga., evitando la atenuación de la señal por división de tensión. Esta ventaja no se limita a los amplificadores de tensión, sino que se pueden disponer mejoras análogas en la adaptación para amplificadores de corriente, amplificadores de transconductancia y amplificadores de transresistencia.
Para explicar estos efectos de la retroalimentación sobre las impedancias, primero una digresión sobre cómo la teoría de dos puertos aborda la determinación de la resistencia y luego su aplicación al amplificador en cuestión.
Antecedentes de la determinación de la resistencia
La Figura 6 muestra un circuito equivalente para encontrar la resistencia de entrada de un amplificador de voltaje de retroalimentación (izquierda) y para un amplificador de corriente de retroalimentación (derecha). Estos arreglos son aplicaciones típicas del teorema de Miller.
En el caso del amplificador de tensión, la tensión de salida βVout de la red de realimentación se aplica en serie y con polaridad opuesta a la tensión de entrada Vx viajando por el bucle (pero con respecto a tierra, las polaridades son las mismas). Como resultado, el voltaje efectivo a través y la corriente a través de la resistencia de entrada del amplificador Rin disminuyen de modo que la resistencia de entrada del circuito aumenta (se podría decir que Ren aparentemente aumenta). Su nuevo valor se puede calcular aplicando el teorema de Miller (para voltajes) o las leyes básicas del circuito. Por lo tanto, la ley de voltaje de Kirchhoff proporciona:
- Vx=IxRin+β β vout,{displaystyle V_{x}=I_{x}R_{mathrm {in}+beta v_{mathrm {out}}
donde vfuera = Av vdentro = Av Ix Ren. Sustituyendo este resultado en la ecuación anterior y resolviendo la resistencia de entrada del amplificador de realimentación, el resultado es:
- Rin()fb)=VxIx=()1+β β Av)Rin.{displaystyle R_{mathrm}(fb)={frac {V_{x} {I_{x}}=left(1+beta} ¿Qué?
La conclusión general de este ejemplo y un ejemplo similar para el caso de la resistencia de salida es: Una conexión de retroalimentación en serie en la entrada (salida) aumenta la resistencia de entrada (salida) por un factor (1 + β AOL), donde AOL = ganancia de lazo abierto.
Por otro lado, para el amplificador de corriente, la corriente de salida βIout de la red de realimentación se aplica en paralelo y con dirección opuesta a la corriente de entrada Yox. Como resultado, la corriente total que fluye a través de la entrada del circuito (no solo a través de la resistencia de entrada Rin) aumenta y el voltaje a través de ella disminuye, de modo que la resistencia de entrada del circuito disminuye. (Rin aparentemente disminuye). Su nuevo valor se puede calcular aplicando el teorema dual de Miller (para corrientes) o las leyes básicas de Kirchhoff:
- Ix=VinRin+β β iout.{displaystyle I_{x}={frac {V_{mathrm {in} }{R_{mathrm {in} }beta i_{mathrm {out} }
donde ifuera = Ai identro = Ai Vx / Ren. Sustituyendo este resultado en la ecuación anterior y resolviendo la resistencia de entrada del amplificador de realimentación, el resultado es:
- Rin()fb)=VxIx=Rin()1+β β Ai).{displaystyle R_{mathrm}(fb)={frac {fnK} {fnMicroc}} {fnMicroc}} {fnK}} {fnK}}} {fnK}}} {fnK}}}} {fnK}} {fnK}}}} {fnf}}}}} {fnKf}}} {f}}}}}}}}}}}}}} {f}}}}}} {f}}}}}}} {f}}}}}}}}} {\f}}}}}}}}}}}}}}}}}}}}}}}} {f}}} {f} {\fnf} {\fnf}}fn\\fnfnfnf}f}fnfnfnfnfnfnfnfnfnfnf}}}fn [R_{mathrm {in} {left(1+beta A_{i}}}
La conclusión general de este ejemplo y un ejemplo similar para el caso de la resistencia de salida es: Una conexión de retroalimentación paralela en la entrada (salida) disminuye la resistencia de entrada (salida) por un factor (1 + β AOL), donde AOL = ganancia de lazo abierto.
Estas conclusiones se pueden generalizar para tratar casos con unidades Norton o Thévenin arbitrarias, cargas arbitrarias y redes generales de retroalimentación de dos puertos. Sin embargo, los resultados dependen de que el amplificador principal tenga una representación de dos puertos; es decir, los resultados dependen de la misma corriente que entra y sale de los terminales de entrada y, del mismo modo, la misma corriente que sale de un terminal de salida debe entrar en el otro terminal de salida.
Una conclusión más amplia, independiente de los detalles cuantitativos, es que la retroalimentación se puede usar para aumentar o disminuir la impedancia de entrada y salida.
Aplicación al amplificador de ejemplo
Estos resultados de resistencia ahora se aplican al amplificador de la Figura 3 y la Figura 5. El factor de mejora que reduce la ganancia, a saber (1 + βFB AOL), decide directamente el efecto de la realimentación sobre las resistencias de entrada y salida del amplificador. En el caso de una conexión en derivación, la impedancia de entrada se reduce por este factor; y en el caso de conexión en serie, la impedancia se multiplica por este factor. Sin embargo, la impedancia que se modifica por la retroalimentación es la impedancia del amplificador en la Figura 5 con la retroalimentación apagada, e incluye las modificaciones a la impedancia causadas por las resistencias de la red de retroalimentación.
Por lo tanto, la impedancia de entrada vista por la fuente con la retroalimentación desactivada es Rin = R1 = R11 || RB || rπ1, y con la retroalimentación activada (pero sin retroalimentación)
- Rin=R11+β β FBAOL,{displaystyle R_{mathrm {in} }={frac {fnh}{1+{beta {fnK}
donde se usa división porque la conexión de entrada es derivación: los dos puertos de retroalimentación están en paralelo con la fuente de señal en el lado de entrada del amplificador. Un recordatorio: AOL es la ganancia de bucle abierto cargada que se encuentra arriba, modificada por las resistencias de la red de retroalimentación.
La impedancia vista por la carga necesita más discusión. La carga de la figura 5 está conectada al colector del transistor de salida y, por lo tanto, está separada del cuerpo del amplificador por la impedancia infinita de la fuente de corriente de salida. Por lo tanto, la retroalimentación no tiene efecto sobre la impedancia de salida, que sigue siendo simplemente RC2 como se ve en la resistencia de carga RL en la Figura 3.
Si, en cambio, quisiéramos encontrar la impedancia presentada en el emisor del transistor de salida (en lugar de su colector), que está conectado en serie a la red de retroalimentación, la retroalimentación aumentaría esta resistencia por la mejora factor (1 + βFB AOL).
Tensión de carga y corriente de carga
La ganancia derivada arriba es la ganancia actual en el colector del transistor de salida. Para relacionar esta ganancia con la ganancia cuando el voltaje es la salida del amplificador, observe que el voltaje de salida en la carga RL está relacionado con la corriente del colector por Ohm's ley como vL = iC (RC2 || RL). En consecuencia, la ganancia de transresistencia vL / iS se encuentra multiplicando la ganancia de corriente por R C2 || DL:
- vLiS=AFB()RC2∥ ∥ RL).{displaystyle {frac {fnMicrom} {L}}{i_{mathrm {S}}=A_{mathrm {FB} (R_{mathrm {C2}parallel R_{mathrm {L}).}
Del mismo modo, si la salida del amplificador se toma como la corriente en la resistencia de carga RL, la división de corriente determina la corriente de carga y la ganancia es entonces:
- iLiS=AFBRC2RC2+RL.{displaystyle {frac {fnMicrom} {L}}{i_{mathrm {S}}=A_{mathrm {FB}{frac} {fnMicrom} {C2} {R_{mathrm {C2}+R_{mathrm}.
¿El bloque amplificador principal es de dos puertos?
Siguen algunos inconvenientes del enfoque de dos puertos, destinados al lector atento.
La Figura 7 muestra el esquema de señal pequeña con el amplificador principal y los dos puertos de retroalimentación en cuadros sombreados. El dos puertos de realimentación satisface las condiciones del puerto: en el puerto de entrada, Iin entra y sale del puerto, y de la misma manera en la salida, Ifuera entra y sale.
¿El bloque amplificador principal también es de dos puertos? El amplificador principal se muestra en el recuadro superior sombreado. Las conexiones a tierra están etiquetadas. La Figura 7 muestra el hecho interesante de que el amplificador principal no satisface las condiciones del puerto en su entrada y salida a menos que se elijan las conexiones a tierra para que eso suceda. Por ejemplo, en el lado de entrada, la corriente que ingresa al amplificador principal es IS. Esta corriente se divide de tres maneras: a la red de retroalimentación, a la resistencia de polarización RB y a la resistencia base del transistor de entrada rπ. Para satisfacer la condición del puerto para el amplificador principal, los tres componentes deben volver al lado de entrada del amplificador principal, lo que significa que todos los cables de tierra etiquetados como G1 deben estar conectado, así como el cable del emisor GE1. Asimismo, en el lado de salida, todas las conexiones a tierra G2 deben estar conectadas y también la conexión a tierra GE2. Luego, en la parte inferior del esquema, debajo de los dos puertos de retroalimentación y fuera de los bloques amplificadores, G1 está conectado a G2. Eso obliga a las corrientes de tierra a dividirse entre los lados de entrada y salida según lo planeado. Tenga en cuenta que esta disposición de conexión divide el emisor del transistor de entrada en un lado de la base y un lado del colector, algo físicamente imposible de hacer, pero eléctricamente el circuito ve todas las conexiones a tierra como un solo nodo. así que esta ficción está permitida.
Por supuesto, la forma en que se conectan los cables de tierra no afecta al amplificador (son todos un nodo), pero sí afecta a las condiciones del puerto. Esta artificialidad es una debilidad de este enfoque: se necesitan las condiciones del puerto para justificar el método, pero el circuito realmente no se ve afectado por la forma en que se intercambian las corrientes entre las conexiones a tierra.
Sin embargo, si ningún arreglo posible de las condiciones del terreno conduce a las condiciones del puerto, es posible que el circuito no se comporte de la misma manera. Los factores de mejora (1 + βFB AOL) para determinar la impedancia de entrada y salida podrían no funcionar. Esta situación es incómoda, porque la falla al hacer dos puertos puede reflejar un problema real (simplemente no es posible), o reflejar una falta de imaginación (por ejemplo, simplemente no pensó en dividir el nodo emisor en dos). Como consecuencia, cuando las condiciones del puerto están en duda, al menos dos enfoques son posibles para establecer si los factores de mejora son precisos: simule un ejemplo utilizando Spice y compare los resultados con el uso de un factor de mejora, o calcule la impedancia utilizando una fuente de prueba. y comparar resultados.
Una opción más práctica es abandonar por completo el enfoque de dos puertos y utilizar varias alternativas basadas en la teoría del gráfico de flujo de señales, incluido el método de Rosenstark, el método de Choma y el uso del teorema de Blackman. Esa elección puede ser aconsejable si los modelos de dispositivos de pequeña señal son complejos o no están disponibles (por ejemplo, los dispositivos se conocen solo numéricamente, tal vez a partir de mediciones o de simulaciones SPICE).
Fórmulas de amplificadores de retroalimentación
Resumiendo el análisis de retroalimentación de dos puertos, uno puede obtener esta tabla de fórmulas.
| Amplificador de retroalimentación | Fuente Signal | Signal de salida | Función de transferencia | Resistencia de entrada | Resistencia al producto |
|---|---|---|---|---|---|
| Series-Shunt (amplificador de tensión) | Voltaje | Voltaje | Avf=VoVi=Av1+β β vAv{displaystyle A_{vf}={frac {fnK} {fnK}} {fnMicroc}}} {fnK}} {f}}}} {f}} {fn}}} {fnK}}}}}}} {fnf}}}}}} {fnf}}} {fnKf}}}}} {f}}}}}}}}}}}} {f}}}}} {f}}}}}}}} {f}}}}}}}} {f}}}} {f} {f} {f}}}}}}}}}}}}}}}}}}}} {f}} {f}}} {f}}}}}}}f}} {f}}}}}}f}}}}}f}}}}}}}}}f}}}}}}f} {f} {f} {f}}fn {A_{v}{1+beta ¿Qué? | Ri()1+β β vAv){displaystyle R_{i}(1+beta _{v}A_{v}} | Ro1+β β vAv{displaystyle {frac {f}{1+beta} ¿Qué? |
| Serie Shunt (amplificador corriente) | Corriente | Corriente | Aif=IoIi=Ai1+β β iAi{displaystyle A_{if}={frac {fnK} {fnK}} {fnMicroc}}} {f}} {fnK}} {f}}} {fnK}}}}} {f}}}}} {fnf}}} {f}}} {f}}}}}}} {fnf}}}}}} {f}} {f}}}}}}}}}}} {f}}}}}}}}}}}} {f} {f} {f} {f} {f} {f} {f}f}f}f}f}f}f}}}f}f}fnf}fnf}}}f}}}}}fnf}f}}}}}}}}}}f}}f}f}f}f}f}f}f}f}}}}}} {A_{i}{1+beta - Sí. | Ri1+β β iAi{displaystyle {frac {f}{1+beta} - Sí. | Ro()1+β β iAi){displaystyle R_{o}(1+beta) ¿Qué? |
| Serie-Series(amplificador de transferencia) | Voltaje | Corriente | Agf=IoVi=Ag1+β β zAg{displaystyle A_{gf}={frac {I_{o}{V_{i}}={frac} {A_{g}{1+beta - Sí. | Ri()1+β β zAg){displaystyle R_{i}(1+beta _{z}A_{g}} | Ro()1+β β zAg){displaystyle R_{o}(1+beta _{z}A_{g}} |
| Shunt-Shunt (amplificador de resistencia) | Corriente | Voltaje | Azf=VoIi=Az1+β β gAz{displaystyle A_{zf}={frac {fnK} {fnK}} {fnMicroc}}}} {f}} {fnK}}} {f}}} {fn}}} {fnK}}}}} {fnf}}}}}} {fnf}}}} {fnKf}}}}} {f}}}}} {f}}}}}}}}} {f}}}}}}}}}} {f}}}}}}} {f}} {f}} {f}}}} {f}}}}}}}}}}}}}}}}}}}}} {f} {f} {f} {f}}} {f}}} {f}f}f}f}f}}f}f}}}}}}f}}}}f}f}}}f}f}}}}}}} {A_{z}{1+beta ¿Qué? | Ri1+β β gAz{displaystyle {frac {f}{1+beta} ¿Qué? | Ro1+β β gAz{displaystyle {frac {f}{1+beta} ¿Qué? |
Las variables y sus significados son
A{displaystyle A}- Ganancia, I{displaystyle Yo...- actual, V{displaystyle V}- Tensión,β β {displaystyle beta }- Ganancia de comentarios y R{displaystyle R.- resistencia.
Los subíndices y sus significados son
f{displaystyle f}- Amplificador de retroalimentación, v{displaystyle v}- Tensión,g{displaystyle g}- transconductancia, Z{displaystyle Z}- Transresistencia, o{displaystyle o}- producción y i{displaystyle i}- corriente para ganancias y comentarios y i{displaystyle i}- entrada para resistencias.
Por ejemplo Avf{displaystyle A_{vf}significa aumento de amplificador de retroalimentación de voltaje.
Distorsión
Los amplificadores simples, como la configuración de emisor común, tienen principalmente una distorsión de orden bajo, como los armónicos 2 y 3. En los sistemas de audio, estos pueden ser mínimamente audibles porque las señales musicales ya son típicamente una serie de armónicos, y los productos de distorsión de bajo orden están ocultos por el efecto de enmascaramiento del sistema auditivo humano.
Después de aplicar cantidades moderadas de retroalimentación negativa (10–15 dB), los armónicos de orden bajo se reducen, pero se introducen armónicos de orden más alto. Dado que estos tampoco están enmascarados, la distorsión empeora audiblemente, aunque el THD general puede disminuir. Esto ha llevado a un mito persistente de que la retroalimentación negativa es perjudicial para los amplificadores de audio, lo que ha llevado a los fabricantes de audiófilos a comercializar sus amplificadores como "retroalimentación cero" (incluso cuando usan retroalimentación local para linealizar cada etapa).
Sin embargo, a medida que aumenta aún más la cantidad de retroalimentación negativa, todos los armónicos se reducen, devolviendo la distorsión a la inaudibilidad y luego mejorándola más allá de la etapa original de retroalimentación cero (siempre y cuando el sistema sea estrictamente estable). Entonces, el problema no es la retroalimentación negativa, sino la cantidad insuficiente de ella.
Referencias y notas
- ^ Santiram Kal (2004). Electrónica básica: Dispositivos, circuitos y fundamentos de TI (Paperback ed.). Prentice-Hall of India Pvt Ltd. pp. 191 ff. ISBN 978-8120319523.
- ^ Kuo, Benjamin C. " Farid Golnaraghi (2003). Sistemas de control automático (Eighth ed.). Wiley. p. 46. ISBN 0-471-13476-7.
- ^ Palumbo, Gaetano " Salvatore Pennisi (2002). Amplificadores de retroalimentación: teoría y diseño. Boston/Dordrecht/Londres: Kluwer Academic. p. 64. ISBN 0-7923-7643-9.
- ^ Jung, Walt (2005). Op Amp Applications Handbook. ISBN 9780750678445.
- ^ Negro, H. S. (enero de 1934). "Amplificadores de retroalimentación estabilizada" (PDF). Bell System Tech. J. Telegraph. 13 (1): 1–18. doi:10.1002/j.1538-7305.1934.tb00652.x. Retrieved 2 de enero 2013.
- ^ Negro, Harold (1937-12-21). "Patente estadounidense 2,102,671: Sistema de traducción de onda" (PDF). www.eepatents.com. Archivado desde el original (PDF) el 2014-10-06.
- ^ Actualmente en exhibición en Bell Laboratories en Mountainside, Nueva Jersey.
- ^ Waldhauer, Fred (1982). Retroalimentación. Wiley. p. 3. ISBN 0-471-05319-8.
- ^ Negro, Harold (diciembre de 1977). "Inventar el amplificador de retroalimentación negativa". IEEE Spectrum.
- ^ Malik, Norbert R. (enero de 1995). Circuitos electrónicos: Análisis, Simulación y Diseño. Prentice Hall. ISBN 9780023749100.
- ^ Lu, L. H. "La estructura de la retroalimentación general" (PDF). Archivado desde el original (PDF) el 2016-06-05.
- ^ Self, Douglas (2013-06-18). Diseño amplificador de potencia de audio (6 ed.). Nueva York: Focal Press. p. 54. ISBN 9780240526133.
- ^ Horowitz, Pablo; Hill, Winfield (1989-07-28). El arte de la electrónica (2 ed.). Cambridge University Press. p. 23. ISBN 9780521370950.
- ^ "MT-044 Op Amp Open Loop Gain y Open Loop Gain Nonlinearity" (PDF). Dispositivos analógicos.
β es la atenuación de retroalimentación, o factor de retroalimentación... ganancia de ruido es igual a 1/β
- ^ R. W. Brodersen. Diseño de circuitos analógicos: conferencias sobre estabilidad.
- ^ Willy M. C. Sansen (2006). Es esencial de diseño analógico. Nueva York; Berlín: Springer. pp. §0513-§0533, p. 155–165. ISBN 0-387-25746-2.
- ^ Partha Pratim Sahu (2013). "§8.2 Partición". VLSI Design. McGraw Hill Education. p. 253. ISBN 9781259029844.
dividir un circuito en partes más pequeñas...[so]...el número de conexiones entre partes se minimiza
- ^ Gaetano Palumbo; Salvatore Pennisi (2002). Amplificadores de retroalimentación: Teoría y Diseño. Springer Science & Business Media. ISBN 9780792376439.
En casos reales, lamentablemente, los bloques no pueden ser considerados unidireccionales.
- ^ Wai-Kai Chen (2009). "§1.2 Métodos de análisis". Retroalimentación, circuitos no lineales y distribuidos. CRC Press. pp. 1–3. ISBN 9781420058826.
- ^ Donald O. Pederson; Kartikeya Mayaram (2007). "§5.2 Retroalimentación para un amplificador general". Analog Integrated Circuitos de Comunicación: Principios, Simulación y Diseño. Springer Science " Business Media. pp. 105 ff. ISBN 9780387680309.
- ^ Scott K. Burgess " John Choma, Jr. "§6.3 (PDF). Análisis generalizado del circuito de retroalimentación. Archivado desde el original (PDF) el 2014-12-30.
- ^ Gaetano Palumbo " Salvatore Pennisi (2002). Amplificadores de retroalimentación: teoría y diseño. Springer Science & Business Media. p. 66. ISBN 9780792376439.
- ^ a b c Arnaldo D’Amico, Christian Falconi, Gianluca Giustolisi, Gaetano Palumbo (abril de 2007). "Resistencia de la retroalimentación Amplificadores: Una representación novedosa" (PDF). Transacciones IEEE en circuitos y sistemas – II Expresos. 54 (4): 298–302. CiteSeerX10.1.1.694.8450. doi:10.1109/TCSII.2006.889713. S2CID 10154732.
{{cite journal}}: CS1 maint: múltiples nombres: lista de autores (link) - ^ Para una introducción, vea Rahul Sarpeshkar (2010). "Capítulo 10: Análisis de la relación de retorno". Ultra Low Power Bioelectronics: Fundamentals, Biomedical Applications, and Bio-Inspired Systems. Cambridge University Press. pp. 240 ff. ISBN 9781139485234.
- ^ Wai-Kai Chen (2005). "§11.2 Métodos de análisis". Amplificador de análisis de circuitos y retroalimentación Teoría. CRC Press. pp. 11–2 ff. ISBN 9781420037272.
- ^ Gaetano Palumbo; Salvatore Pennisi (2002). "§3.3 El Método Rosenstark y §3.4 El Método Choma". Amplificadores de retroalimentación: Teoría y Diseño. Springer Science " Business Media. pp. 69 ff. ISBN 9780792376439.
- ^ J. Choma, Jr (abril de 1990). "Análisis de flujo de señales de redes de retroalimentación". Transacciones IEEE en circuitos y sistemas. 37 (4): 455-463. Bibcode:1990ITCS...37..455C. doi:10.1109/31.52748.
- ^ Richard C Jaeger (1997). "Figura 18.2". Diseño de circuitos microelectrónicos (International ed.). McGraw-Hill. p. 986. ISBN 9780070329225.
ediciones:BZ69IvJlfW8C.
- ^ Ashok K. Goel. Feedback topologies Archived 2008-02-29 at the Wayback Machine.
- ^ Zimmer T., Geoffroy D. Amplificador de retroalimentación.
- ^ Vivek Subramanian. Conferencias sobre comentarios Archivado 2008-02-29 en el Wayback Machine.
- ^ P. R. Gray; P. J. Hurst; S. H. Lewis; R. G. Meyer (2001). Análisis y diseño de circuitos integrados analógicos (Cuarta edición). Nueva York: Wiley. pp. 586-587. ISBN 0-471-32168-0.
- ^ A. S. Sedra; K. C. Smith (2004). Circuitos microelectrónicos (Fifth ed.). Nueva York: Oxford. Ejemplo 8.4, págs. 825 a 829 y simulación de PSpice, págs. 855 a 859. ISBN 0-19-514251-9.
- ^ a b c Neaman, Donald. Neamen Electronic Circuit Analysis And Design (4th ed.). pp. 851–946. Capítulo 12.
- ^ Si se incluye el feedforward, su efecto es causar una modificación de la ganancia de apertura, normalmente tan pequeña en comparación con la ganancia de apertura en sí misma que puede ser bajada. Observe también que el bloque amplificador principal es unilateral.
- ^ El uso del factor de mejora (1 + βFB AOL) requiere atención, especialmente para el caso de impedancia de salida utilizando retroalimentación de series. Ver Jaeger, nota abajo.
- ^ R.C. Jaeger " T.N. Blalock (2006). Diseño de circuito microelectrónico (Tercera edición). McGraw-Hill Professional. Ejemplo 17.3 págs. 1092 a 1096. ISBN 978-0-07-319163-8.
- ^ Es decir, la impedancia encontrada apagando la fuente de señal IS = 0, insertar una corriente de prueba en el plomo del emisor Ix, encontrar el voltaje a través de la fuente de prueba Vx, y encontrar RFuera. = Vx / Ix.
- ^ La equivalencia del bloque amplificador principal a una red de dos puertos garantiza que los factores de rendimiento funcionan, pero sin esa equivalencia pueden funcionar de todos modos. Por ejemplo, en algunos casos el circuito se puede mostrar equivalente a otro circuito que es un puerto de dos, por "recoger" diferentes parámetros de circuito que son funciones de los originales. ¡No hay fin a la creatividad!
- ^ Richard C Jaeger; Travis N Blalock (2004). "§18.7: Errores comunes en la aplicación de la teoría de comentarios de dos puertos". Diseño de circuitos microelectrónicos (2a edición). McGraw=Hill Higher Education. pp. 1409 ff. ISBN 0072320990.
Se debe ejercer un gran cuidado en la aplicación de la teoría de dos puertos para asegurar que las redes de retroalimentación amplificador puedan realmente ser representadas como dos puertos
- ^ Gaetano Palumbo; Salvatore Pennisi (2002). Amplificadores de retroalimentación: Teoría y Diseño. Springer Science & Business Media. p. 66. ISBN 9780792376439.
- ^ "Distorsión y percepción no lineales en frecuencias bajas". Audioholics Home Theater, HDTV, Receptores, Altavoces, Blu-ray Reseñas y Noticias13 de agosto de 2015. Retrieved 2016-04-18.
La mayor parte de la distorsión armónica ha sido enmascarada, sin embargo, un par de armónicos de alto orden estaban lo suficientemente lejos en frecuencia y lo suficientemente fuerte para ser escuchado. Así que para determinar la audibilidad de la distorsión armónica, tenemos que saber cuánto enmascaramiento se hace por diferentes tonos a diferentes niveles de ruido.
- ^ de Santis, Eric Mario; Henin, Simon (2007-06-07). "Percepción " Umbrales de la distorsión no lineal usando señales complejas " (PDF).
El enmascaramiento es un concepto de principio en la percepción de la distorsión, ya que los productos de distorsión sólo contribuirán al percepto de la distorsión si no están enmascarados por el estímulo primario u otros productos de distorsión.
- ^ a b Pass, Nelson (2008-11-01). "Distorsión auditiva y retroalimentación - Passlabs". passlabs.com. Retrieved 2016-04-18.
Aquí vemos que como bajas cifras de retroalimentación se aplican a una sola etapa de ganancia las dos declinaciones armónicas linealmente con la retroalimentación, pero se crean mayores cantidades de armónicos de orden superior. A medida que aumenta la retroalimentación sobre alrededor de 15 dB o así, todas estas formas de distorsión [decline] en proporción al aumento de la retroalimentación.
- ^ a b Putzeys, Bruno. "Retroalimentación negativa en amplificadores de audio: Por qué no hay tal cosa como demasiado (Parte 2)". EDN. Retrieved 2016-04-18.
Por supuesto este experimento da la impresión de que más retroalimentación es peor. Tienes que superar ese golpe. Apenas cualquiera que lo haya probado así ha oído la mejora inevitable (y francamente mágica) que sucede una vez que usted consigue más allá, diga 20 o 30dB. A partir de ahí se obtiene una mejora neta inequívoca que continúa para siempre.
- ^ "Theta Digital – Amplificador III desperdiciado". www.thetadigital.com. Archivado desde el original el 21 de julio de 2015. Retrieved 2016-04-18.
Dreadnaught III no utiliza ninguna retroalimentación negativa global.
- ^ Martin Colloms (enero de 1998). "¿Un futuro sin retroalimentación?" (PDF). Stereophile. Archivado desde el original (PDF) en 2013-06-19. Retrieved 9 de mayo 2007.
- ^ P. J. Baxandall, “Diseño amplificador de potencia de audio, Wireless World, 1978.
- ^ Bruno Putzeys (febrero de 2011). "La palabra 'F', o por qué no hay tal cosa como demasiado retroalimentación" (PDF). Audio lineal. Retrieved 19 de marzo 2013.
Contenido relacionado
Medición de flujo
Sistema en un chip
Arbusto Vannevar