Altura de escala

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

En ciencias atmosféricas, terrestres y planetarias, una altura de escala, generalmente denotado por la letra capital H, es una distancia (vertical o radial) sobre la cual una cantidad física disminuye por un factor de e (la base de logaritmos naturales, aproximadamente 2.718).

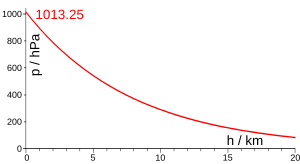
Altura de escala utilizada en un modelo de presión atmosférica simple

Para las atmósferas planetarias, la altura de escala es el aumento de altitud para el cual la presión atmosférica disminuye en un factor de e. La altura de la escala permanece constante para una temperatura particular. Se puede calcular mediante

{displaystyle H={frac {k_{text{B}}T}{mg}}}

{displaystyle H={frac {RT}{Mg}}}

k_B = Pertzmann constante = 1.381×10^{,23 a 23} J⋅K⁻¹
R = constante de gas
T = temperatura atmosférica media en kelvins = 250 K para la Tierra
m = masa media de una molécula (unidades kg)
M = masa media de un grupo de partículas atmosféricas = 0,029 kg/mol para la Tierra
g = aceleración debido a la gravedad en la ubicación actual (m/s²)

La presión (fuerza por unidad de área) a una altitud determinada es el resultado del peso de la atmósfera suprayacente. Si a una altura de z la atmósfera tiene densidad ρ y presión P, entonces se mueve hacia arriba una altura infinitamente pequeña dz > disminuirá la presión en una cantidad dP, igual al peso de una capa de atmósfera de espesor dz.

Así:

{displaystyle {frac {dP}{dz}}=-grho }

gdzgMT

{displaystyle rho ={frac {MP}{RT}}}

La combinación de estas ecuaciones da

{displaystyle {frac {dP}{P}}={frac {-dz}{frac {k_{text{B}}T}{mg}}}}

{displaystyle {frac {dP}{P}}=-{frac {dz}{H}}}

P₀zz

{displaystyle P=P_{0}exp left(-{frac {z}{H}}right)}

Esto se traduce como que la presión disminuye exponencialmente con la altura.

En la atmósfera de la Tierra, la presión al nivel del mar P₀ tiene un promedio de 1.01×10⁵ Pa , la masa molecular media del aire seco es 28,964 u y, por tanto, m = 28,964 × 1,660×10⁻²⁷ = 4.808×10⁻²⁶ kg. En función de la temperatura, la altura de escala de la atmósfera terrestre es, por tanto, H/T = k/mg = (1,38/(4,808×9,81))×10³ = 29,26 m/K. Esto produce las siguientes alturas de escala para temperaturas del aire representativas.

T = 290 K, H = 8500 m
T = 273 K, H = 8000 m
T = 260 K, H = 7610 m
T = 210 K, H = 6000 m

Estas cifras deben compararse con la temperatura y la densidad de la atmósfera terrestre trazadas en NRLMSISE-00, que muestra que la densidad del aire cae de 1200 g/m³ al nivel del mar a 0,5 ³ = 0,125 g/m³ a 70 km, un factor de 9600, lo que indica una altura de escala promedio de 70/ln(9600) = 7,64 km, consistente con lo indicado La temperatura media del aire en ese rango es cercana a los 260 K.

Nota:

La densidad está relacionada con la presión por las leyes de gas ideales. Por lo tanto, la densidad también disminuirá exponencialmente con altura desde un valor de nivel del mar ***₀ aproximadamente igual a 1,2 kg m⁻³
En alturas superiores a 100 km, un ambiente puede ya no estar bien mezclado. Entonces cada especie química tiene su propia altura de escala.
Aquí se suponía que la temperatura y la aceleración gravitacional eran constantes, pero ambos pueden variar a grandes distancias.

Ejemplos planetarios

A continuación se muestran las alturas aproximadas a escala atmosférica de cuerpos seleccionados del Sistema Solar.

Venus: 15,9 km
Tierra: 8,5 km
Marte: 11,1 km
Júpiter: 27 km
Saturno: 59,5 km
- Titan: 21 km
Urano: 27,7 km
Neptuno: 19.1–20.3 km
Plutón: ~50 km

Altura de escala para un disco delgado

Para un disco de gas alrededor de un objeto central condensado, como, por ejemplo, una protoestrella, se puede derivar una altura de escala del disco que es algo análoga a la altura de la escala planetaria. Comenzamos con un disco de gas que tiene una masa pequeña en relación con el objeto central. Suponemos que el disco está en equilibrio hidrostático con la componente z de la gravedad de la estrella, donde la componente de gravedad apunta al plano medio del disco:

{displaystyle {frac {dP}{dz}}=-{frac {GM_{*}rho z}{(r^{2}+z^{2})^{3/2}}}}

donde:

G = constante gravitacional 6.674×10^{−11 -} m³⋅kg⁻¹⋅s⁻²
r = la coordinación cilíndrica radial para la distancia desde el centro de la estrella o objeto centralmente condensado
z = la coordenada cilíndrica de altura/altura para la distancia del medio plano del disco (o centro de la estrella)
M_* = la masa del objeto estrella/centralmente condensado
P = la presión del gas en el disco
${displaystyle rho }$ = la densidad de masa de gas en el disco

En la aproximación del disco delgado, ${displaystyle zll r}$ y la ecuación de equilibrio hidrostático

{displaystyle {frac {dP}{dz}}approx -{frac {GM_{*}rho z}{r^{3}}}}

Para determinar la presión del gas, se puede utilizar la ley de los gases ideales:

{displaystyle P={frac {rho k_{text{B}}T}{bar {m}}}}

T = la temperatura del gas en el disco, donde la temperatura es una función r, pero independiente de z
${displaystyle {bar {m}}}$ = la masa molecular media del gas

Usando la ley de los gases ideales y la ecuación de equilibrio hidrostático, se obtiene:

{displaystyle {frac {drho }{dz}}approx -{frac {GM_{*}{bar {m}}rho z}{kTr^{3}}}}

{displaystyle rho =rho _{0}exp left(-left({frac {z}{h_{D}}}right)^{2}right)}

{displaystyle rho _{0}}

{displaystyle h_{D}}

{displaystyle h_{D}={sqrt {frac {2kTr^{3}}{GM_{*}{bar {m}}}}}approx 0.0306{sqrt {frac {left(T/100 {text{K}}right)left(r/1{text{ au}}right)^{3}}{left(M_{*}/M_{odot }right)left({bar {m}}/2{text{ amu}}right)}}} {text{ au}}}

{displaystyle M_{odot }}

{displaystyle {text{au}}}

{displaystyle {text{amu}}}

Como aproximación ilustrativa, si ignoramos la variación radial de la temperatura, ${displaystyle T}$ , vemos que ${displaystyle h_{D}propto r^{3/2}}$ y que el disco aumenta en altitud mientras uno se mueve radialmente lejos del objeto central.

Debido a la suposición de que la temperatura del gas en el disco, T, es independiente de z, ${displaystyle h_{D}}$ a veces se conoce como la altura de la escala del disco esotérmico.

Altura de la escala del disco en un campo magnético

Un campo magnético en un disco de gas delgado alrededor de un objeto central puede cambiar la altura de la escala del disco. Por ejemplo, si un disco no perfectamente conductor gira a través de un campo magnético poloidal (es decir, el campo magnético inicial es perpendicular al plano del disco), entonces se generará un campo magnético toroidal (es decir, paralelo al plano del disco). producido dentro del disco, que pellizcar y comprimirá el disco. En este caso, la densidad del gas del disco es:

{displaystyle rho (r,z)=rho _{0}(r)exp left(-left({frac {z}{h_{D}}}right)^{2}right)-rho _{text{cut}}(r)left[1-exp left(-left({frac {z}{h_{D}}}right)^{2}right)right]}

cortado

{displaystyle rho _{text{cut}}}

{displaystyle rho _{rm {cut}}(r)=(mu _{0}sigma _{D}r)^{2}left({frac {B_{z}^{2}}{mu _{0}}}right)left({frac {Omega _{*}}{Omega _{K}}}-1right)^{2}}

${displaystyle mu _{0}}$ es la permeabilidad del espacio libre
${displaystyle sigma _{D}}$ es la conductividad eléctrica del disco
${displaystyle B_{z}}$ es la densidad del flujo magnético del campo poloidal en el ${displaystyle z}$ dirección
${displaystyle Omega _{*}}$ es la velocidad angular de rotación del objeto central (si el campo magnético poloidal es independiente del objeto central entonces ${displaystyle Omega _{*}}$ se puede establecer a cero)
${displaystyle Omega _{K}}$ es la velocidad angular keplerian del disco a una distancia ${displaystyle r}$ del objeto central.

Estas fórmulas dan la altura máxima, ${displaystyle H_{B}}$ , del disco magnetizado como

{displaystyle H_{B}=h_{D}{sqrt {ln left(1+rho _{0}/rho _{rm {cut}}right)}},}

{displaystyle h_{B}}

{displaystyle h_{B}=h_{D}{sqrt {ln left(1+{frac {1-1/e}{1/e+rho _{text{cut}}/rho _{0}}}right)}}.}

Contenido relacionado

Más resultados...