Altitud (triángulo)

ImprimirCitar

segmento de línea perpendicular del lado del triángulo al vértice opuesto

Las tres altitudes de un triángulo se intersecten en el ortocenter, que para un triángulo agudo está dentro del triángulo.

En geometría, una altitud de un triángulo es un segmento de línea que pasa por un vértice y es perpendicular a (es decir, que forma un ángulo recto con) una línea que contiene la base (el lado opuesto al vértice). Esta línea que contiene el lado opuesto se llama la base extendida de la altitud. La intersección de la base extendida y la altura se llama pie de la altura. La longitud de la altitud, a menudo llamada simplemente "la altitud", es la distancia entre la base extendida y el vértice. El proceso de dibujar la altitud desde el vértice hasta el pie se conoce como dejar caer la altitud en ese vértice. Es un caso especial de proyección ortogonal.

Las altitudes se pueden usar en el cálculo del área de un triángulo: la mitad del producto de la longitud de una altitud y la longitud de su base es igual al área del triángulo. Así, la altura más larga es perpendicular al lado más corto del triángulo. Las alturas también se relacionan con los lados del triángulo a través de las funciones trigonométricas.

En un triángulo isósceles (un triángulo con dos lados congruentes), la altura que tiene el lado incongruente como base tendrá el punto medio de ese lado como pie. También la altura que tiene por base el lado incongruente será la bisectriz del ángulo del vértice.

Es común marcar la altitud con la letra $h$ (como en height), a menudo subíndice con el nombre del lado al que se dibuja la altitud.

La altitud de un triángulo derecho desde su ángulo recto hasta su hipotenusa es la media geométrica de las longitudes de los segmentos en que se divide la hipotenusa. Usando el teorema de Pitágoras en los 3 triángulos de los lados ()p+q, r, s), ()r, p, h) y ()s, h, q),

{displaystyle {begin{aligned}(p+q)^{2};;&=quad r^{2};;,+quad s^{2}\p^{2}!!+!2pq!+!q^{2}&=overbrace {p^{2}!!+!h^{2}} +overbrace {h^{2}!!+!q^{2}} \2pqquad ;;;&=2h^{2};therefore h!=!{sqrt {pq}}\end{aligned}}}

En un triángulo rectángulo, la altura trazada a la hipotenusa $c$ divide la hipotenusa en dos segmentos de longitudes $p$ y $q$ . Si denotamos la longitud de la altitud por $h c$ , entonces tenemos la relación

h_c=sqrt{pq}

(Teorema geométrico medio)

En un triángulo derecho, la altitud de cada ángulo agudo coincide con una pierna e interseca el lado opuesto a (tiene su pie a) el vértice en ángulo recto, que es el ortocentro.

Las altitudes de cada uno de los ángulos agudos de un triángulo obtuso se encuentran completamente fuera del triángulo, al igual que el ortocentro

H

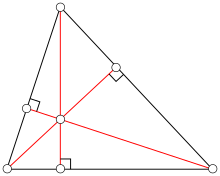
Para los triángulos acutángulos, los pies de las alturas caen todos sobre los lados del triángulo (no extendidos). En un triángulo obtuso (uno con un ángulo obtuso), el pie de la altura al vértice del ángulo obtuso cae en el interior del lado opuesto, pero los pies de las alturas a los vértices del ángulo agudo caen en el lado opuesto extendido, exterior al triángulo. Esto se ilustra en el diagrama adyacente: en este triángulo obtuso, una altura caída perpendicularmente desde el vértice superior, que tiene un ángulo agudo, se cruza con el lado horizontal extendido fuera del triángulo.

Ortocentro

Tres altitudes intersecándose en el ortocentro

Las tres altitudes (posiblemente extendidas) se intersecan en un solo punto, llamado ortocentro del triángulo, generalmente indicado por $H$ . El ortocentro se encuentra dentro del triángulo si y solo si el triángulo es agudo. Si un ángulo es un ángulo recto, el ortocentro coincide con el vértice en el ángulo recto.

Vamos $A$ , $B$ , $C$ denotar los vértices y también los ángulos del triángulo, y dejar ${displaystyle a=left|{overline {BC}}right|,b=left|{overline {CA}}right|,c=left|{overline {AB}}right|}$ sean las longitudes laterales. El ortocenter tiene coordenadas trilineales

{displaystyle {begin{aligned}&sec A:sec B:sec C\&=cos A-sin Bsin C:cos B-sin Csin A:cos C-sin Asin B,end{aligned}}}

y coordenadas baricéntricas

{displaystyle {begin{aligned}&(a^{2}+b^{2}-c^{2})(a^{2}-b^{2}+c^{2}):(a^{2}+b^{2}-c^{2})(-a^{2}+b^{2}+c^{2}):(a^{2}-b^{2}+c^{2})(-a^{2}+b^{2}+c^{2})\&=tan A:tan B:tan C.end{aligned}}}

Dado que las coordenadas baricéntricas son todas positivas para un punto en el interior de un triángulo pero al menos una es negativa para un punto en el exterior, y dos de las coordenadas baricéntricas son cero para un punto de vértice, las coordenadas baricéntricas dadas para el ortocentro, muestre que el ortocentro está en el interior de un triángulo agudo, en el vértice del ángulo recto de un triángulo rectángulo y en el exterior de un triángulo obtuso.

En el plano complejo, deje que los puntos $A$ , $B$ , $C$ representan los números $z A$ , $z B$ , $z C$ y supongamos que el circuncentro del triángulo $△ ABC$ se encuentra en el origen del plano. Entonces, el número complejo

{displaystyle z_{H}=z_{A}+z_{B}+z_{C}}

está representado por el punto $H$ , es decir, la altura del triángulo $△ ABC$ . A partir de esto, se pueden establecer de forma sencilla las siguientes caracterizaciones del ortocentro $H$ mediante vectores libres:

{displaystyle {vec {OH}}=sum limits _{scriptstyle {rm {cyclic}}}{vec {OA}},qquad 2cdot {vec {HO}}=sum limits _{scriptstyle {rm {cyclic}}}{vec {HA}}.}

La primera de las identidades vectoriales anteriores también se conoce como el problema de Sylvester, propuesto por James Joseph Sylvester.

Propiedades

Sea $D$ , $E$ , $F$ indican los pies de las altitudes desde $A$ , $B$ , $C$ respectivamente. Entonces:

El producto de las longitudes de los segmentos en los que el ortocentro divide una altitud es el mismo para las tres altitudes:

{displaystyle {overline {AH}}cdot {overline {HD}}={overline {BH}}cdot {overline {HE}}={overline {CH}}cdot {overline {HF}}.}

El círculo se centró en

H

tener radio la raíz cuadrada de esta constante es el círculo polar del triángulo.

La suma de las proporciones sobre las tres alturas de la distancia del ortocentro de la base a la longitud de la altitud es 1: (Esta propiedad y la siguiente son aplicaciones de una propiedad más general de cualquier punto interior y los tres cevianos a través de ella.)

{displaystyle {frac {overline {HD}}{overline {AD}}}+{frac {overline {HE}}{overline {BE}}}+{frac {overline {HF}}{overline {CF}}}=1.}

La suma de las proporciones en las tres alturas de la distancia del ortocentro del vértice a la longitud de la altitud es 2:

{displaystyle {frac {overline {AH}}{overline {AD}}}+{frac {overline {BH}}{overline {BE}}}+{frac {overline {CH}}{overline {CF}}}=2.}

El conjugado isogonal del ortocentro es el circuncentro del triángulo.

El conjugado isotómico del ortocentro es el punto simmediano del triángulo anticomplementario.

Cuatro puntos en el plano, tal que uno de ellos es el ortocentro del triángulo formado por los otros tres, se llama un sistema ortocéntrico o cuadrángulo ortocéntrico.

Relación con círculos y cónicas

Denote el circunradio del triángulo con $R$ . Entonces

{displaystyle a^{2}+b^{2}+c^{2}+{overline {AH}}^{2}+{overline {BH}}^{2}+{overline {CH}}^{2}=12R^{2}.}

Además, al indicar $r$ como el radio del incírculo del triángulo, $r a, r b, r c$ como los radios de sus excircles, y $R$ nuevamente como el radio de su circuncircunferencia, se cumplen las siguientes relaciones con respecto a las distancias del ortocentro a los vértices:

{displaystyle {begin{aligned}&r_{a}+r_{b}+r_{c}+r={overline {AH}}+{overline {BH}}+{overline {CH}}+2R,\&r_{a}^{2}+r_{b}^{2}+r_{c}^{2}+r^{2}={overline {AH}}^{2}+{overline {BH}}^{2}+{overline {CH}}^{2}+(2R)^{2}.end{aligned}}}

Si hay alguna altitud, por ejemplo, $AD$ , se extiende para intersectar el círculo circunscrito en $P$ , de modo que $AD$ es una cuerda del circuncírculo, luego el pie $D$ biseca el segmento $HP$ :

{displaystyle {overline {HD}}={overline {DP}}.}

Las directrices de todas las parábolas que son tangentes externamente a un lado de un triángulo y tangentes a las extensiones de los otros lados pasan por el ortocentro.

Una circuncónica que pasa por el ortocentro de un triángulo es una hipérbola rectangular.

Relación con otros centros, el círculo de nueve puntos

El ortocentro $H$ , el centroide $G$ , el circuncentro $O$ , y el centro $N$ del círculo de nueve puntos se encuentran en una sola línea, conocida como la línea de Euler. El centro del círculo de nueve puntos se encuentra en el punto medio de la línea de Euler, entre el ortocentro y el circuncentro, y la distancia entre el centroide y el circuncentro es la mitad de la distancia entre el centroide y el ortocentro:

{displaystyle {begin{aligned}&{overline {OH}}=2{overline {NH}},\&2{overline {OG}}={overline {GH}}.end{aligned}}}

El ortocentro está más cerca del incentro $I$ que del baricentro, y el ortocentro está más lejos que el incentro del centroide:

<math alttext="{displaystyle {begin{aligned}{overline {HI}}&{overline {IG}}.end{aligned}}}" xmlns="http://www.w3.org/1998/Math/MathML">HĪ ̄ .HḠ ̄ ,HḠ ̄ ■IḠ ̄ .{displaystyle {begin{aligned}{overline {HI} {overline {hG}}\{overline {HG}}} {f}}}} {end{aligned}}}}}} {f}} {f}}}<img alt="{displaystyle {begin{aligned}{overline {HI}}&{overline {IG}}.end{aligned}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/64cdc9504853c98273088f70b3060eed204729ff" style="vertical-align: -2.838ex; width:12.507ex; height:6.843ex;"/>

En términos de los lados $a$ , $b$ , $c$ , inradius $r$ y circunradio $R$ ,

{displaystyle {begin{aligned}{overline {OH}}^{2}&=R^{2}-8R^{2}cos Acos Bcos C\&=9R^{2}-(a^{2}+b^{2}+c^{2}),\{overline {HI}}^{2}&=2r^{2}-4R^{2}cos Acos Bcos C.end{aligned}}}

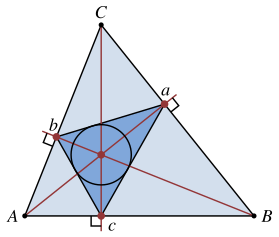
Triángulo órtico

Triángulo

 abc

(respectivamente,

 DEF

en el texto) es el triángulo ortico del triángulo

 ABC

Si el triángulo $△ ABC$ es oblicuo (no contiene un ángulo recto), el triángulo pedal del ortocentro del triángulo original es llamado triángulo órtico o triángulo de altura. Es decir, los pies de las alturas de un triángulo oblicuo forman el triángulo órtico, $△ DEF$ . Además, el incentro (el centro del círculo inscrito) del triángulo órtico $△ DEF$ es el ortocentro del triángulo original $△ ABC$ .

Las coordenadas trilineales de los vértices del triángulo órtico están dadas por

{displaystyle {begin{aligned}D&=0:sec B:sec C\E&=sec A:0:sec C\F&=sec A:sec B:0.end{aligned}}}

Los lados prolongados del triángulo órtico se encuentran con los lados opuestos prolongados de su triángulo de referencia en tres puntos colineales.

En cualquier triángulo acutángulo, el triángulo inscrito con el perímetro más pequeño es el triángulo órtico. Esta es la solución al problema de Fagnano, planteado en 1775. Los lados del triángulo órtico son paralelos a las tangentes a la circunferencia circunscrita en los vértices del triángulo original.

El triángulo órtico de un triángulo acutángulo da un recorrido de luz triangular.

Las líneas tangentes del círculo de nueve puntos en los puntos medios de los lados de $△ ABC$ son paralelas a los lados del triángulo órtico, formando un triángulo similar al triángulo órtico.

El triángulo ortónico está estrechamente relacionado con el triángulo tangencial, construido como sigue: $L A$ ser la línea tangente al círculo del triángulo $ ABC$ en vertex $A$ , y definir $L B, L C$ analógicamente. Vamos ${displaystyle A''=L_{B}cap L_{C},}$ ${displaystyle B''=L_{C}cap L_{A},}$ ${displaystyle C''=L_{C}cap L_{A}.}$ El triángulo tangencial $ A"B"C"$ , cuyos lados son los tangentes al triángulo $ ABC$ 's circuncircle en sus vértices; es homotético al triángulo orthic. El circumcenter del triángulo tangencial, y el centro de similitud de los triángulos ortónicos y tangenciales, están en la línea Euler.

Las coordenadas trilineales de los vértices del triángulo tangencial están dadas por

{displaystyle {begin{aligned}A''&=-a:b:c\B''&=a:-b:c\C''&=a:b:-c.end{aligned}}}

El triángulo de referencia y su triángulo órtico son triángulos ortológicos.

Para obtener más información sobre el triángulo órtico, consulte aquí.

Algunos teoremas de altitud adicionales

Altitud en términos de los lados

Para cualquier triángulo con los lados $a, b, c$ y semiperímetro ${displaystyle s={tfrac {a+b+c}{2}},}$ la altitud del lado $a$ es dado por

h_a=frac{2sqrt{s(s-a)(s-b)(s-c)}}{a}.

Esto se deriva de combinar la fórmula de Heron para el área de un triángulo en términos de los lados con la fórmula de área ${displaystyle {tfrac {1}{2}}times {text{base}}times {text{height}},}$ donde se toma la base como parte $a$ y la altura es la altitud desde $A$ .

Teoremas del inradio

Considere un triángulo arbitrario con lados $a, b, c$ y con los correspondientes altitudes $h a, h b, h c . Las altitudes y el radio del círculo r están relacionados por$

displaystyle frac{1}{r}=frac{1}{h_a}+frac{1}{h_b}+frac{1}{h_c}.

Teorema del circunradio

Denotando la altitud desde un lado de un triángulo como $h a$ , los otros dos lados como $b$ y $c$ , y el circunradio del triángulo (radio del círculo circunscrito del triángulo) como $R$ , la altitud es dada por

h_a=frac{bc}{2R}.

Punto interior

Si $p 1, p 2, p 3$ son las distancias perpendiculares desde cualquier punto $P$ a los lados y $h 1, h 2, h 3$ son las alturas a los lados respectivos, entonces

frac{p_1}{h_1} +frac{p_2}{h_2} + frac{p_3}{h_3} = 1.

Teorema del área

Denotar las altitudes de cualquier triángulo de los lados $a, b, c$ respectivamente $h a, h b, h c$ , y denotar la semi-sum de las reciprocas de las alturas como ${displaystyle H={tfrac {h_{a}^{-1}+h_{b}^{-1}+h_{c}^{-1}}{2}}}$ tenemos

mathrm{Area}^{-1} = 4 sqrt{H(H-h_a^{-1})(H-h_b^{-1})(H-h_c^{-1})}.

Punto general sobre una altitud

Si $E$ es cualquier punto en una altitud $AD$ de cualquier triángulo $△ ABC$ , entonces

{displaystyle {overline {AC}}^{2}+{overline {EB}}^{2}={overline {AB}}^{2}+{overline {CE}}^{2}.}

Casos especiales

Triángulo equilátero

Para cualquier punto $P$ dentro de un triángulo equilátero, la suma de las perpendiculares a los tres lados es igual a la altura de el triangulo. Este es el teorema de Viviani.

Triángulo rectángulo

Comparación del teorema pitagórico inverso con el teorema pitagórico

En un triángulo rectángulo las tres altitudes $h a h b h c$ (los dos primeros de los cuales equivalen a las longitudes de los lados $b$ y $a$ respectivamente) están relacionados según

frac{1}{h_a ^2}+frac{1}{h_b ^2}=frac{1}{h_c ^2}.

Esto también se conoce como el teorema inverso de Pitágoras.

Historia

El teorema de que las tres alturas de un triángulo concurren (en el ortocentro) no se establece directamente en los textos matemáticos griegos sobrevivientes, pero se usa en el Libro de los Lemas (proposición 5), atribuido a Arquímedes (siglo III a. C.), citando el "comentario al tratado sobre los triángulos rectángulos", obra que no se conserva. También fue mencionado por Pappus (Mathematical Collection, VII, 62; c. 340). El teorema fue declarado y probado explícitamente por al-Nasawi en su comentario (siglo XI) sobre el Libro de los Lemas, y atribuido a al-Quhi (fl. siglo X).

Esta demostración en árabe se tradujo como parte de las ediciones latinas (principios del siglo XVII) del Libro de los lemas, pero no era muy conocida en Europa y, por lo tanto, el teorema se demostró varias veces más. en el siglo XVII-XIX. Samuel Marolois lo demostró en su Geometrie (1619), e Isaac Newton lo demostró en un tratado inconcluso Geometry of Curved Lines (c. 1680). Posteriormente William Chapple lo demostró en 1749.

Una demostración particularmente elegante se debe a François-Joseph Servois (1804) e independientemente a Carl Friedrich Gauss (1810): Dibuje una línea paralela a cada lado del triángulo a través del punto opuesto, y forme un nuevo triángulo a partir de las intersecciones de estas tres líneas. Entonces el triángulo original es el triángulo medial del nuevo triángulo, y las alturas del triángulo original son las bisectrices perpendiculares del nuevo triángulo, y por lo tanto coinciden (en el circuncentro del nuevo triángulo).

Contenido relacionado

Más resultados...