Algoritmo de Smith-Waterman
El algoritmo Smith-Waterman realiza una alineación de secuencia local; es decir, para determinar regiones similares entre dos cadenas de secuencias de ácidos nucleicos o secuencias de proteínas. En lugar de observar la secuencia completa, el algoritmo de Smith-Waterman compara segmentos de todas las longitudes posibles y optimiza la medida de similitud.
El algoritmo fue propuesto por primera vez por Temple F. Smith y Michael S. Waterman en 1981. Al igual que el algoritmo Needleman-Wunsch, del cual es una variación, Smith-Waterman es un algoritmo de programación dinámica. Como tal, tiene la propiedad deseable de que se garantiza encontrar la alineación local óptima con respecto al sistema de puntuación que se utiliza (que incluye la matriz de sustitución y el esquema de puntuación de brechas). La principal diferencia con el algoritmo Needleman-Wunsch es que las celdas de la matriz de puntuación negativa se establecen en cero, lo que hace visibles las alineaciones locales (por lo tanto, con puntuación positiva). El procedimiento de rastreo comienza en la celda de la matriz con la puntuación más alta y continúa hasta encontrar una celda con puntuación cero, lo que produce la alineación local con la puntuación más alta. Debido a su complejidad de tiempo cúbico, a menudo no se puede aplicar en la práctica a problemas de gran escala y se reemplaza en favor de alternativas computacionalmente más eficientes como (Gotoh, 1982), (Altschul y Erickson, 1986) y (Myers y Miller, 1988).
Historia
En 1970, Saul B. Needleman y Christian D. Wunsch propusieron un algoritmo de homología heurista para alineación de secuencias, también conocido como el algoritmo Needleman-Wunsch. Es un algoritmo de alineación global que requiere O()mn){displaystyle O(mn)} pasos de cálculo (m{displaystyle m} y n{displaystyle n} son las longitudes de las dos secuencias que se alinean). Utiliza el cálculo iterativo de una matriz para mostrar alineación global. En la década siguiente, Sankoff, Reichert, Beyer y otros formularon algoritmos heurísticos alternativos para analizar secuencias genéticas. Los vendedores introdujeron un sistema para medir distancias de secuencia. En 1976, Waterman et al. añadieron el concepto de lagunas en el sistema de medición original. En 1981, Smith y Waterman publicaron su algoritmo Smith-Waterman para calcular la alineación local.
El algoritmo Smith-Waterman es bastante exigente del tiempo: Para alinear dos secuencias de longitudes m{displaystyle m} y n{displaystyle n}, O()m2n){displaystyle O(m^{2}n)} Se requiere tiempo. Gotoh y Altschul optimizaron el algoritmo O()mn){displaystyle O(mn)} pasos. La complejidad espacial fue optimizada por Myers y Miller desde O()mn){displaystyle O(mn)} a O()n){displaystyle O(n)} (linear), donde n{displaystyle n} es la longitud de la secuencia más corta, para el caso donde sólo se desea una de las muchas alineaciones óptimas posibles. Chowdhury, Le, y Ramachandran posteriormente optimizaron el rendimiento de caché del algoritmo manteniendo el uso del espacio lineal en la longitud total de las secuencias de entrada.
Motivación
En los últimos años, los proyectos genómicos realizados en una variedad de organismos generaron cantidades masivas de datos de secuencias de genes y proteínas, lo que requiere análisis computacional. El alineamiento de secuencias muestra las relaciones entre genes o entre proteínas, lo que lleva a una mejor comprensión de su homología y funcionalidad. La alineación de secuencias también puede revelar dominios y motivos conservados.
Una motivación para la alineación local es la dificultad de obtener alineaciones correctas en regiones de baja similitud entre secuencias biológicas distantemente relacionadas, porque las mutaciones han añadido demasiado ruido durante el tiempo evolutivo para permitir una comparación significativa de esas regiones. La alineación local evita por completo esas regiones y se centra en aquellas con una puntuación positiva, es decir, aquellas con una señal de similitud conservada evolutivamente. Un requisito para la alineación local es una puntuación de expectativa negativa. La puntuación de expectativa se define como la puntuación media que el sistema de puntuación (matricidad de sustitución y penalizaciones de brecha) produciría para una secuencia aleatoria.
Otra motivación para utilizar alineamientos locales es que existe un modelo estadístico confiable (desarrollado por Karlin y Altschul) para alineamientos locales óptimos. La alineación de secuencias no relacionadas tiende a producir puntuaciones de alineación local óptimas que siguen una distribución de valores extremos. Esta propiedad permite a los programas producir un valor esperado para el alineamiento local óptimo de dos secuencias, que es una medida de la frecuencia con la que dos secuencias no relacionadas producirían un alineamiento local óptimo cuya puntuación es mayor o igual a la puntuación observada. Los valores esperados muy bajos indican que las dos secuencias en cuestión podrían ser homólogas, lo que significa que podrían compartir un ancestro común.
Algoritmo
Vamos. A=a1a2...an{displaystyle A=a_{1}a_{2}a_{n} y B=b1b2...bm{displaystyle B=b_{1}b_{2}...b_{m} ser las secuencias a alinearse, donde n{displaystyle n} y m{displaystyle m} son las longitudes de A{displaystyle A} y B{displaystyle B} respectivamente.
- Determinar la matriz de sustitución y el esquema de la sanción.
- s()a,b){displaystyle s(a,b)} - La puntuación de la similitud de los elementos que constituyeron las dos secuencias
- Wk{displaystyle W_{k} - La pena de una brecha que tiene longitud k{displaystyle k}
- Construir una matriz de puntuación H{displaystyle H. e inicializar su primera fila y primera columna. El tamaño de la matriz de puntuación es ()n+1)Alternativa Alternativa ()m+1){displaystyle (n+1)*(m+1)}. La matriz utiliza la indexación basada en 0.
- Hk0=H0l=0for0≤ ≤ k≤ ≤ nand0≤ ≤ l≤ ≤ m{displaystyle H_{k0}=H_{0l=0quad forquad 0leq kleq nquad andquad 0leq lleq m}
- Llene la matriz de puntuación usando la ecuación de abajo.
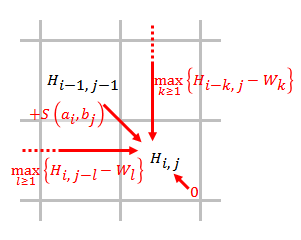
- Hij=max{}Hi− − 1,j− − 1+s()ai,bj),maxk≥ ≥ 1{}Hi− − k,j− − Wk},maxl≥ ≥ 1{}Hi,j− − l− − Wl},0()1≤ ≤ i≤ ≤ n,1≤ ≤ j≤ ≤ m){displaystyle H_{ij}=max {begin{cases}H_{i-1,j-1}+s(a_{i},b_{j}),max _{kgeq 1}{H_{i-k, ¿Qué? 1}end{cases}qquad (1leq ileq n,1leq jleq m)}
- Donde
- Hi− − 1,j− − 1+s()ai,bj){displaystyle H_{i-1,j-1}+s(a_{i},b_{j}} es la puntuación de alineación ai{displaystyle A_{i} y bj{displaystyle B_{j},
- Hi− − k,j− − Wk{displaystyle H... J. es la puntuación si ai{displaystyle A_{i} está al final de una brecha de longitud k{displaystyle k},
- Hi,j− − l− − Wl{displaystyle H_{i,j-l}-W_{l} es la puntuación si bj{displaystyle B_{j} está al final de una brecha de longitud l{displaystyle l},
- 0{displaystyle 0} significa que no hay similitud ai{displaystyle A_{i} y bj{displaystyle B_{j}.
- Traceback. Empezando por la puntuación más alta en la matriz de puntuación H{displaystyle H. y terminando en una célula matriz que tiene una puntuación de 0, trazaback basado en la fuente de cada puntuación recursivamente para generar la mejor alineación local.
Explicación
El algoritmo Smith-Waterman alinea dos secuencias por partidos/mismatches (también conocidos como sustituciones), inserciones y eliminaciones. Tanto las inserciones como las supresiones son las operaciones que introducen lagunas, que están representadas por dashes. El algoritmo Smith-Waterman tiene varios pasos:
- Determinar la matriz de sustitución y el plan de penalización de las diferencias. Una matriz de sustitución asigna cada par de bases o aminoácidos una puntuación para el partido o el desajuste. Por lo general los partidos obtienen puntajes positivos, mientras que los desajustes obtienen calificaciones relativamente inferiores. Una función de penalización de brecha determina el costo de puntuación para abrir o ampliar las brechas. Se sugiere que los usuarios elijan el sistema de puntuación adecuado basado en los objetivos. Además, también es una buena práctica probar diferentes combinaciones de matrices de sustitución y multas.
- Inicia la matriz de puntuación. Las dimensiones de la matriz de puntuación son 1+longitud de cada secuencia respectivamente. Todos los elementos de la primera fila y la primera columna están fijados a 0. La primera fila extra y la primera columna hacen posible alinear una secuencia a otra en cualquier posición, y establecerlos a 0 hace que la brecha terminal libre de penalización.
- Scoring. Puntuar cada elemento de izquierda a derecha, de arriba a abajo en la matriz, considerando los resultados de las sustituciones (puntos diagonales) o agregando brechas (puntos horizontales y verticales). Si ninguna de las puntuaciones son positivas, este elemento obtiene un 0. De lo contrario se utiliza la puntuación más alta y se registra la fuente de esa puntuación.
- Traceback. Partiendo del elemento con la puntuación más alta, trazaback basado en la fuente de cada partitura recursivamente, hasta que se encuentre 0. Los segmentos que tienen la puntuación más alta de similitud basada en el sistema de puntuación dado se genera en este proceso. Para obtener la segunda mejor alineación local, aplicar el proceso de trazaback comenzando en la segunda puntuación más alta fuera del trazo de la mejor alineación.
Comparación con el algoritmo Needleman-Wunsch
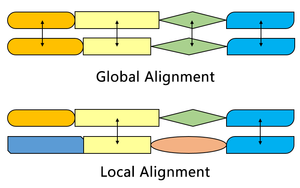
El algoritmo de Smith-Waterman encuentra los segmentos en dos secuencias que tienen similitudes, mientras que el algoritmo de Needleman-Wunsch alinea dos secuencias completas. Por lo tanto, tienen diferentes propósitos. Ambos algoritmos utilizan los conceptos de matriz de sustitución, función de penalización de brecha, matriz de puntuación y proceso de rastreo. Tres diferencias principales son:
| algoritmo Smith-Waterman | algoritmo de Needleman-Wunsch | |
|---|---|---|
| Iniciación | Primera fila y primera columna se establece a 0 | Primera fila y primera columna están sujetas a penalización de brecha |
| Scoring | La puntuación negativa se establece en 0 | La puntuación puede ser negativa |
| Traceback | Empieza con la puntuación más alta, termina cuando 0 se encuentra | Comience con la célula en la parte inferior derecha de la matriz, termine en la parte superior izquierda de la célula |
Una de las distinciones más importantes es que no se asigna ninguna puntuación negativa en el sistema de puntuación del algoritmo Smith-Waterman, lo que permite la alineación local. Cuando algún elemento tiene una puntuación inferior a cero, significa que las secuencias hasta esa posición no tienen similitudes; este elemento luego se establecerá en cero para eliminar la influencia de la alineación anterior. De esta manera, el cálculo puede continuar encontrando alineación en cualquier posición posteriormente.
La matriz de puntuación inicial del algoritmo de Smith-Waterman permite la alineación de cualquier segmento de una secuencia con una posición arbitraria en la otra secuencia. Sin embargo, en el algoritmo Needleman-Wunsch, también es necesario considerar la penalización del espacio final para alinear las secuencias completas.
Matriz de sustitución
A cada sustitución de base o de aminoácido se le asigna una puntuación. En general, a los partidos se les asignan puntuaciones positivas y a los desajustes se les asignan puntuaciones relativamente más bajas. Tomemos como ejemplo la secuencia de ADN. Si las coincidencias obtienen +1 y las discrepancias obtienen -1, entonces la matriz de sustitución es:
| A | G | C | T | |
|---|---|---|---|---|
| A | 1 | -1 | -1 | -1 |
| G | -1 | 1 | -1 | -1 |
| C | -1 | -1 | 1 | -1 |
| T | -1 | -1 | -1 | 1 |
Esta matriz de sustitución puede describirse como: s()ai,bj)={}+1,ai=bj− − 1,aiل ل bj{displaystyle s(a_{i},b_{j})={begin{cases}+1,quad a_{i}=b_{j}-1,quad a_{i}neq ¿Qué?
Diferentes sustituciones de bases o sustituciones de aminoácidos pueden tener puntuaciones diferentes. La matriz de sustitución de los aminoácidos suele ser más complicada que la de las bases. Ver PAM, BLOSUM.
Penalización por hueco
La penalización por brecha designa puntuaciones por inserción o eliminación. Una estrategia simple de penalización por brecha es utilizar una puntuación fija para cada brecha. En biología, sin embargo, la puntuación debe contarse de forma diferente por razones prácticas. Por un lado, la similitud parcial entre dos secuencias es un fenómeno común; por otro lado, un evento de mutación de un solo gen puede resultar en la inserción de un único espacio largo. Por lo tanto, las brechas conectadas que forman una brecha larga generalmente son más favorecidas que múltiples brechas cortas y dispersas. Para tener en cuenta esta diferencia, se han añadido al sistema de puntuación los conceptos de apertura y ampliación de huecos. La puntuación de apertura de la brecha suele ser más alta que la puntuación de la extensión de la brecha. Por ejemplo, los parámetros predeterminados en EMBOSS Water son: apertura del espacio = 10, extensión del espacio = 0,5.
Aquí discutimos dos estrategias comunes para la penalización de la brecha. Vea la pena Gap para más estrategias. Vamos. Wk{displaystyle W_{k} ser la función de la penalización de la brecha de longitud k{displaystyle k}:
Lineal
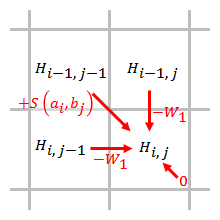
Una penalización por espacio lineal tiene las mismas puntuaciones por abrir y ampliar un espacio:
Wk=kW1{displaystyle ¿Qué?,
Donde W1{displaystyle W_{1} es el costo de una sola brecha.
La penalización del espacio es directamente proporcional a la longitud del espacio. Cuando se utiliza una penalización de espacio lineal, el algoritmo de Smith-Waterman se puede simplificar a:
Hij=max{}Hi− − 1,j− − 1+s()ai,bj),Hi− − 1,j− − W1,Hi,j− − 1− − W1,0{displaystyle H_{ij}=max {begin{cases}H_{i-1,j-1}+s(a_{i},b_{j}),H_{i-1,j}-W_{1},H_{i,j-1}-W_{1},end{cases}}}
El algoritmo simplificado utiliza O()mn){displaystyle O(mn)} pasos. Cuando un elemento está siendo anotado, sólo es necesario considerar las sanciones de brecha de los elementos que están directamente adyacentes a este elemento.
Afín
Una sanción de la brecha afine considera la apertura y la ampliación separadamente:
0,v>0)}" xmlns="http://www.w3.org/1998/Math/MathML">Wk=uk+v()u■0,v■0){displaystyle ¿Qué?0,v>0)}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/f241c1ed6acf91d8e53301807bbac6b234147eee" style="vertical-align: -0.838ex; width:29.035ex; height:2.843ex;"/>,
Donde v{displaystyle v} es la pena de apertura de brechas, y u{displaystyle u} es la pena de extensión. Por ejemplo, la pena por una diferencia de longitud 2 es 2u+v{displaystyle 2u+v}.
Se utilizó una penalización de brecha arbitraria en el papel original del algoritmo Smith-Waterman. Utiliza O()m2n){displaystyle O(m^{2}n)} pasos, por lo tanto es bastante exigente del tiempo. Gotoh ha optimizado los pasos para una penalización de afinamiento O()mn){displaystyle O(mn)}, pero el algoritmo optimizado sólo intenta encontrar una alineación óptima, y la alineación óptima no está garantizada a ser encontrada. Altschul modificó el algoritmo de Gotoh para encontrar todas las alineaciones óptimas manteniendo la complejidad computacional. Más tarde, Myers y Miller señalaron que el algoritmo de Gotoh y Altschul puede ser modificado en base al método que fue publicado por Hirschberg en 1975, y aplicado este método. El algoritmo de Myers y Miller puede alinear dos secuencias usando O()n){displaystyle O(n)} espacio, con n{displaystyle n} ser la longitud de la secuencia más corta. Chowdhury, Le, and Ramachandran later showed how to run Gotoh's algoritmo cache-efficiently in linear space using a different recursive divide-and-conquer strategy than the one used by Hirschberg. El algoritmo resultante funciona más rápido que el algoritmo de Myers y Miller en la práctica debido a su rendimiento de caché superior.
Gap penalty example
Tome la alineación de las secuencias TACGGGCCCGCTAC y TAGCCCTATCGGTCA como ejemplo. Cuando se utiliza la función de penalización de espacio lineal, el resultado es (Alineaciones realizadas por EMBOSS Water. La matriz de sustitución es DNAfull (puntuación de similitud: +5 para caracteres coincidentes; de lo contrario, -4). La apertura y extensión del espacio son 0,0 y 1,0 respectivamente):
TACGGGCCCGCTA-CTA---G-CC-CTATC
Cuando se utiliza una penalización de espacio afín, el resultado es (la apertura y extensión del espacio son 5,0 y 1,0 respectivamente):
TACGGGCCCGCTATA---GCC--CTA
Este ejemplo muestra que una penalización de brecha afín puede ayudar a evitar pequeñas brechas dispersas.
Matriz de puntuación
La función de la matriz de puntuación es realizar comparaciones uno a uno entre todos los componentes en dos secuencias y registrar los resultados de alineación óptimos. El proceso de puntuación refleja el concepto de programación dinámica. La alineación óptima final se encuentra expandiendo iterativamente la alineación óptima creciente. En otras palabras, la alineación óptima actual se genera al decidir qué ruta (coincidencia/desadaptación o inserción de espacio) da la puntuación más alta de la alineación óptima anterior. El tamaño de la matriz es la longitud de una secuencia más 1 por la longitud de la otra secuencia más 1. La primera fila y la primera columna adicionales sirven para alinear una secuencia con cualquier posición de la otra secuencia. Tanto la primera línea como la primera columna se establecen en 0 para que el espacio final no se vea penalizado. La matriz de puntuación inicial es:
| b1 | ... | bj | ... | bm | ||
|---|---|---|---|---|---|---|
| 0 | 0 | ... | 0 | ... | 0 | |
| a1 | 0 | |||||
| ... | ... | |||||
| ai | 0 | |||||
| ... | ... | |||||
| an | 0 |
Ejemplo
Tomemos como ejemplo la alineación de las secuencias de ADN TGTTACGG y GGTTGACTA. Utilice el siguiente esquema:
- Matriz de sustitución: s()ai,bj)={}+3,ai=bj− − 3,aiل ل bj{displaystyle s(a_{i},b_{j})={begin{cases}+3,quad a_{i}=b_{j}-3,quad a_{i}neq ¿Qué?
- Gap penalty: Wk=2k{displaystyle ¿Qué? (a linear gap penalty of W1=2{displaystyle ¿Qué?)
Inicialice y complete la matriz de puntuación, como se muestra a continuación. Esta figura muestra el proceso de puntuación de los tres primeros elementos. El color amarillo indica las bases que se están considerando. El color rojo indica la puntuación más alta posible para la celda que se está puntuando.

La matriz de puntuación terminada se muestra abajo a la izquierda. El color azul muestra la puntuación más alta. Un elemento puede recibir puntuación de más de un elemento, cada uno formará un camino diferente si se rastrea este elemento. En caso de que haya varias puntuaciones más altas, el rastreo se debe realizar comenzando con cada puntuación más alta. El proceso de rastreo se muestra a continuación a la derecha. La mejor alineación local se genera en la dirección inversa.
 | 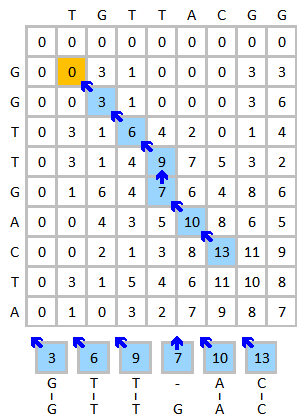 |
| Matriz de puntuación final (la puntuación más alta es en azul) | Traceback proceso y resultado de alineación |
El resultado de la alineación es:
G T T - A C G T G A C
Implementación
Hay una implementación del algoritmo Smith-Waterman, SSEARCH, disponible en el paquete de análisis de secuencia FASTA de UVA FASTA Downloads. Esta implementación incluye código acelerado Altivec para procesadores PowerPC G4 y G5 que acelera las comparaciones entre 10 y 20 veces, utilizando una modificación del enfoque de Wozniak, 1997, y una vectorización SSE2 desarrollada por Farrar que hace que las búsquedas óptimas en bases de datos de secuencias de proteínas sean bastante prácticas. Una biblioteca, SSW, amplía la implementación de Farrar para devolver información de alineación además de la puntuación óptima de Smith-Waterman.
Versiones aceleradas
FPGA
Cray demostró la aceleración del algoritmo Smith-Waterman utilizando una plataforma informática reconfigurable basada en chips FPGA, con resultados que muestran una aceleración de hasta 28 veces en comparación con las soluciones estándar basadas en microprocesadores. Otra versión del algoritmo Smith-Waterman basada en FPGA muestra aceleraciones de FPGA (Virtex-4) de hasta 100 veces en comparación con un procesador Opteron de 2,2 GHz. Los sistemas TimeLogic DeCypher y CodeQuest también aceleran Smith-Waterman y Framesearch mediante tarjetas PCIe FPGA.
Una tesis de maestría de 2011 incluye un análisis de la aceleración de Smith-Waterman basada en FPGA.
En una publicación de 2016, el código OpenCL compilado con Xilinx SDAccel acelera la secuenciación del genoma, supera el rendimiento de CPU/GPU/W entre 12 y 21 veces, y se presentó una implementación muy eficiente. Usando una tarjeta PCIe FPGA equipada con una FPGA Xilinx Virtex-7 2000T, el rendimiento por nivel de vatio fue mejor que el de CPU/GPU entre 12 y 21 veces.
GPU
El Laboratorio Nacional Lawrence Livermore y el Instituto Conjunto del Genoma del Departamento de Energía de los Estados Unidos implementaron una versión acelerada de las búsquedas de alineación de secuencia local Smith-Waterman utilizando unidades de procesamiento de gráficos (GPU) con resultados preliminares que muestran una velocidad 2x -Up sobre implementaciones de software. Desde 1997 ya se implementa un método similar en el software Biofacet, con el mismo factor de aceleración.
También están disponibles varias implementaciones de GPU del algoritmo en la plataforma CUDA C de NVIDIA. En comparación con la implementación de CPU más conocida (que utiliza instrucciones SIMD en la arquitectura x86) de Farrar, las pruebas de rendimiento de esta solución utilizando una sola tarjeta NVidia GeForce 8800 GTX muestran un ligero aumento en el rendimiento para secuencias más pequeñas, pero una ligera disminución en rendimiento para los más grandes. Sin embargo, las mismas pruebas ejecutadas en tarjetas duales NVidia GeForce 8800 GTX son casi el doble de rápidas que la implementación de Farrar para todos los tamaños de secuencia probados.
Ahora está disponible una implementación GPU CUDA más nueva de SW que es más rápida que las versiones anteriores y también elimina las limitaciones en la longitud de las consultas. Ver CUDASW++.
Se han informado once implementaciones de SW diferentes en CUDA, tres de las cuales reportan aceleraciones de 30X.
SIMD
En 2000, en una publicación de Rognes y Seeberg. En contraste con el enfoque de Wozniak (1997), la nueva implementación se basó en vectores paralelos a la secuencia de consulta, no en vectores diagonales. La empresa Sencel Bioinformatics ha solicitado una patente que cubre este enfoque. Sencel está desarrollando aún más el software y proporciona ejecutables para uso académico de forma gratuita.
Ahora está disponible una vectorización SSE2 del algoritmo (Farrar, 2007) que proporciona una aceleración de 8 a 16 veces en procesadores Intel/AMD con extensiones SSE2. Cuando se ejecuta en un procesador Intel utilizando la microarquitectura Core, la implementación SSE2 logra un aumento de 20 veces. La implementación SSE2 de Farrar está disponible como programa SSEARCH en el paquete de comparación de secuencias FASTA. SSEARCH está incluido en el conjunto de programas de búsqueda de similitudes del Instituto Europeo de Bioinformática.
La empresa danesa de bioinformática CLC bio ha logrado aceleraciones cercanas a 200 con respecto a las implementaciones de software estándar con SSE2 en una CPU Intel Core 2 Duo de 2,17 GHz, según un informe técnico disponible públicamente.
La versión acelerada del algoritmo Smith-Waterman, en servidores Linux basados en Intel y Advanced Micro Devices (AMD), es compatible con el paquete GenCore 6, ofrecido por Biocceleration. Las pruebas de rendimiento de este paquete de software muestran una aceleración de hasta 10 veces la velocidad en relación con la implementación de software estándar en el mismo procesador.
CLC bio, actualmente la única empresa de bioinformática que ofrece soluciones SSE y FPGA que aceleran Smith-Waterman, ha logrado aceleraciones de más de 110 con respecto a las implementaciones de software estándar con CLC Bioinformatics Cube.
La implementación más rápida del algoritmo en CPU con SSSE3 se puede encontrar en el software SWIPE (Rognes, 2011), que está disponible bajo la licencia pública general GNU Affero. Paralelamente, este software compara residuos de dieciséis secuencias de bases de datos diferentes con un residuo de consulta. Utilizando una secuencia de consulta de 375 residuos, se logró una velocidad de 106 mil millones de actualizaciones de celda por segundo (GCUPS) en un sistema de procesador dual Intel Xeon X5650 de seis núcleos, que es más de seis veces más rápido que el software basado en Farrar's 's. 39;rayado' acercarse. Es más rápido que BLAST cuando se utiliza la matriz BLOSUM50.
Una implementación de Smith–Waterman denominada diagonalsw, en C y C++, utiliza conjuntos de instrucciones SIMD (SSE4.1 para la plataforma x86 y AltiVec para la plataforma PowerPC). Se publica bajo una licencia MIT de código abierto.
Motor de banda ancha celular
En 2008, Farrar describió una adaptación del sistema Stripe Smith-Waterman al Cell Broadband Engine y reportó velocidades de 32 y 12 GCUPS en un blade IBM QS20 y una Sony PlayStation 3, respectivamente.
Limitaciones
La rápida expansión de los datos genéticos desafía la velocidad de los algoritmos actuales de alineación de secuencias de ADN. Las necesidades esenciales de un método eficiente y preciso para el descubrimiento de variantes de ADN exigen enfoques innovadores para el procesamiento paralelo en tiempo real.
Contenido relacionado
Precisión y exactitud
Evidencia empírica
Teoría del flogisto
































