Algoritmo de Grover

En el cálculo cuántico, Algoritmo de Grover, también conocido como algoritmo de búsqueda cuántica, se refiere a un algoritmo cuántico para la búsqueda no estructurada que encuentra con alta probabilidad la entrada única a una función de caja negra que produce un valor de salida particular, utilizando sólo ${displaystyle O({sqrt {N})}$ evaluaciones de la función, donde ${displaystyle N}$ es el tamaño del dominio de la función. Fue ideado por Lov Grover en 1996.

El problema analógico de la computación clásica no puede resolverse en menos que ${displaystyle O(N)}$ evaluaciones (porque, en promedio, hay que comprobar la mitad del dominio para tener una probabilidad del 50% de encontrar la entrada correcta). Charles H. Bennett, Ethan Bernstein, Gilles Brassard y Umesh Vazirani demostraron que cualquier solución cuántica del problema necesita evaluar la función ${displaystyle Omega ({sqrt {N})}$ tiempos, por lo que el algoritmo de Grover es asintoticamente óptimo. Dado que los algoritmos clásicos para los problemas completos de NP requieren exponencialmente muchos pasos, y el algoritmo de Grover proporciona a la mayoría una velocidad cuadrática sobre la solución clásica para la búsqueda no estructurada, esto sugiere que el algoritmo de Grover por sí mismo no proporcionará soluciones polinomio-tiempo para los problemas completos de NP (como la raíz cuadrada de una función exponencial es una función exponencial, no polinomial).

A diferencia de otros algoritmos cuánticos, que pueden proporcionar velocidad exponencial sobre sus contrapartes clásicas, el algoritmo de Grover proporciona sólo una velocidad cuadrática. Sin embargo, incluso la velocidad cuadrática es considerable cuando ${displaystyle N}$ es grande, y el algoritmo de Grover se puede aplicar para acelerar amplias clases de algoritmos. El algoritmo de Grover podría fuerza bruta una clave criptográfica simétrica de 128 bits en aproximadamente 2⁶⁴ iteraciones, o una llave de 256 bits en aproximadamente 2¹²⁸ iteraciones. Como resultado, a veces se sugiere que se dupliquen las longitudes de clave simétricas para proteger contra futuros ataques cuánticos.

Aplicaciones y limitaciones

El algoritmo de Grover, junto con variantes como la amplificación de amplitud, se puede usar para acelerar una amplia gama de algoritmos. En particular, los algoritmos para problemas NP-completos generalmente contienen una búsqueda exhaustiva como una subrutina, que puede ser acelerada por el algoritmo de Grover. El mejor algoritmo actual para 3SAT es un ejemplo de ello. Los problemas genéricos de satisfacción de restricciones también ven aceleraciones cuadráticas con Grover. Estos algoritmos no requieren que la entrada se proporcione en forma de oráculo, ya que el algoritmo de Grover se aplica con una función explícita, p. la función que comprueba que un conjunto de bits satisface una instancia 3SAT.

El algoritmo de Grover también puede brindar aceleraciones comprobables para problemas de caja negra en la complejidad de consultas cuánticas, incluida la distinción de elementos y el problema de colisión (resuelto con el algoritmo Brassard-Høyer-Tapp). En este tipo de problemas, uno trata la función del oráculo f como una base de datos, y el objetivo es usar la consulta cuántica para esta función la menor cantidad de veces posible.

Criptografía

El algoritmo de Grover resuelve esencialmente la tarea de función de inversión. Roughly speaking, if we have a function ${displaystyle y=f(x)}$ que se puede evaluar en una computadora cuántica, el algoritmo de Grover nos permite calcular ${displaystyle x}$ cuando se da ${displaystyle y}$. En consecuencia, el algoritmo de Grover da una velocidad asintotica amplia a muchos tipos de ataques de fuerza bruta contra la criptografía de clave simétrica, incluyendo ataques de colisión y ataques previos a la imagen. Sin embargo, esto puede no ser necesariamente el algoritmo más eficiente, ya que, por ejemplo, el algoritmo paralelo rho es capaz de encontrar una colisión en SHA2 más eficiente que el algoritmo de Grover.

Limitaciones

El artículo original de Grover describía el algoritmo como un algoritmo de búsqueda de base de datos, y esta descripción sigue siendo común. La base de datos en esta analogía es una tabla de todas las salidas de la función, indexadas por la entrada correspondiente. Sin embargo, esta base de datos no está representada explícitamente. En cambio, se invoca un oráculo para evaluar un elemento por su índice. Leer una base de datos completa elemento por elemento y convertirlo en una representación de este tipo puede llevar mucho más tiempo que la búsqueda de Grover. Para tener en cuenta tales efectos, el algoritmo de Grover puede verse como una solución a una ecuación o como una restricción. En tales aplicaciones, el oráculo es una forma de verificar la restricción y no está relacionado con el algoritmo de búsqueda. Esta separación suele evitar las optimizaciones algorítmicas, mientras que los algoritmos de búsqueda convencionales a menudo se basan en dichas optimizaciones y evitan la búsqueda exhaustiva.

La principal barrera para instanciar una aceleración del algoritmo de Grover es que la aceleración cuadrática lograda es demasiado modesta para superar la gran sobrecarga de las computadoras cuánticas a corto plazo. Sin embargo, las generaciones posteriores de computadoras cuánticas tolerantes a fallas con un mejor rendimiento de hardware pueden realizar estas aceleraciones para instancias prácticas de datos.

Descripción del problema

Como entrada para el algoritmo de Grover, supongamos que tenemos una función ${displaystyle fcolon {0,1,ldotsN-1}to {0,1}}$. En la analogía de la base de datos no estructurada, el dominio representa índices a una base de datos, y f()x) = 1 si y sólo si los datos x puntos para satisfacer el criterio de búsqueda. Asumimos además que sólo un índice de satisfios f()x) = 1, y llamamos este índice ⋅. Nuestro objetivo es identificar ⋅.

Podemos acceder a f con una subrutina (a veces llamada oráculo) en forma de operador unitario U_ω que actúa de la siguiente manera:

${displaystyle {begin{cases}U_{omega } tuvxrangle =- tuvxrangle > {text{for }x=omega {text{, that is, }f(x)=1,U_{omega } animadoxrangle = WordPressxrangle '{for }xneq omega {text{, that is, }f(x)=0.end{cases}}$

Esto utiliza el ${displaystyle N}$-dimensional espacio estatal ${displaystyle {fnMithcal}}$, que es suministrado por un registro con ${displaystyle n=lceil log - No.$ Cubitos. Esto a menudo se escribe como

${displaystyle U_{omega } arrestxrangle =(-1)^{f(x)}$

Salidas del algoritmo de Grover ⋅ con probabilidad al menos 1/2 utilizando ${displaystyle O({sqrt {N})}$ aplicaciones de U_⋅. Esta probabilidad se puede hacer arbitrariamente grande ejecutando el algoritmo de Grover varias veces. Si uno corre el algoritmo de Grover hasta ⋅ se encuentra, el número esperado de aplicaciones todavía ${displaystyle O({sqrt {N})}$, ya que sólo se ejecutará dos veces en promedio.

Definición alternativa de oráculo

Esta sección compara el oráculo anterior ${displaystyle U_{omega }$ con un oráculo ${displaystyle U_{f}$.

U_ω es diferente del oráculo cuántico estándar para una función f. Este oráculo estándar, indicado aquí como U_f, utiliza un sistema auxiliar de qubits. La operación entonces representa una inversión (NO puerta) en el sistema principal condicionada por el valor de f(x) del sistema auxiliar:

${displaystyle {begin{cases}U_{f} arrestxrangle detainedyrangle = WordPressxrangle ¦neg yrangle >{text{for }x=omega {text{,0} que es, }f(x)=1,U_{f}aprendidaxrangle Silencioyrangle = sufrimientoxrangle privyrangle &{text{for }xneq omega {text{, that is, }f(x)=0,end{cases}}}$

o brevemente,

${displaystyle U_{f} sobrevivirxrangle = WordPressxrangle$

Estos oráculos generalmente se realizan sin computar.

Si nos dan U_f como nuestro oráculo, entonces también podemos implementar U_⋅, desde U_⋅ es U_f cuando el codo auxiliar está en el estado ${displaystyle TEN-rangle ={frac {1}{sqrt {2}}{big (}Sobrevivir0rangle - sobrevivir1rangle {big)}=H habit1rangle }$:

$################################################################################################################################################################################################################################################################$

Así que el algoritmo de Grover se puede ejecutar independientemente de cuál oráculo se da. Si U_f se da, entonces debemos mantener un cuarto adicional en el estado ${displaystyle ← }$ y aplicar U_f en lugar de U_⋅.

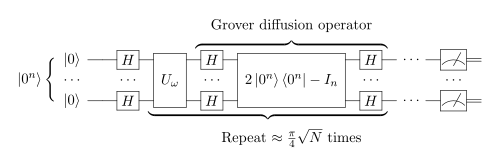
Algoritmo

Representación del circuito cuántico del algoritmo de Grover

Los pasos del algoritmo de Grover son los siguientes:

1. Iniciar el sistema a la superposición uniforme en todos los estados
   ${displaystyle Silenciosrangle ={frac {1}{sqrt {N}}sum} ¿Qué?$
2. Realizar la siguiente "información de la cosecha" ${displaystyle r(N)}$ veces:
   1. Aplicar el operador ${displaystyle U_{omega }$
   2. Aplicar el Difusión de Grover operador ${displaystyle U_{s}=2left bendicionesrightrangle leftlangle sright sometida-I}$
3. Medir el estado cuántico resultante en la base computacional.

Para el valor elegido correctamente ${displaystyle r}$, la salida será ${displaystyle ← }$ con probabilidad acercando 1 para N 1. El análisis muestra que este valor eventual ${displaystyle r(N)}$ satisfizo ${displaystyle r(N)leq {Big lceil }{frac {fnMicroc} } {4} {fn} {fn} {fn} {fn}} {fn}} {fn}} {fn}} {fn} {fn}}}} {fn}} {fn}}} {fn}} {f}}}} {fn}}} {f}}}}}} {f} {f}}}}}}}}}} {\\f}}}}}}} {\f}}}}}}}} {f}}}}} {\f}}}}}}}}}}}}} {\\\\\\\f}}}}}}}}}}}}}}}}}} {\\\\\\\f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} Big rceil }$.

Implementar los pasos para este algoritmo se puede hacer utilizando una serie de puertas lineales en el número de codos. Así, la complejidad de la puerta de este algoritmo es ${displaystyle O(log(N)r(N)}$, o ${displaystyle O(log(N)}$ por iteración.

Prueba geométrica de corrección

Imagen mostrando la interpretación geométrica de la primera iteración del algoritmo de Grover. El vector estatal ${displaystyle Silenciosrangle }$ se gira hacia el vector objetivo ${displaystyle ← }$ como se muestra.

Hay una interpretación geométrica del algoritmo de Grover, siguiendo la observación de que el estado cuántico del algoritmo de Grover permanece en un subespacio bidimensional después de cada paso. Considere el avión atravesado por ${displaystyle Silenciosrangle }$ y ${displaystyle ← }$; equivalentemente, el avión atravesado por ${displaystyle ← }$ y el ket perpendicular ${displaystyle textstyle Silencios'rangle ={frac {1}{sqrt {N-1}}sum _{xneq omega }$.

El algoritmo de Grover comienza con el ket inicial ${displaystyle Silenciosrangle }$, que está en el subespacio. El operador ${displaystyle U_{omega }$ es un reflejo en la ortogonal hiperplano ${displaystyle ← }$ para vectores en el plano azotado por ${displaystyle Silencioso$ y ${displaystyle ← }$, es decir, actúa como un reflejo en ${displaystyle Silencioso$. Esto se puede ver por escrito ${displaystyle U_{omega }$ en la forma de una reflexión del accionistas:

${displaystyle U_{omega }=I-2 sufrimientoomega rangle langle omega Silencio.$

El operador ${displaystyle U_{s}=2 vidasrangle langle s sometida-I}$ es un reflejo ${displaystyle Silenciosrangle }$. Ambos operadores ${displaystyle U_{s}$ y ${displaystyle U_{omega }$ tomar estados en el avión ${displaystyle Silencioso$ y ${displaystyle ← }$ a estados en el avión. Por lo tanto, el algoritmo de Grover permanece en este plano para todo el algoritmo.

Es sencillo comprobar que el operador ${displaystyle U_{s}U_{omega }$ de cada paso de iteración Grover gira el vector del estado por un ángulo ${displaystyle theta =2arcsin {tfrac {1}{sqrt {N}}}$. Así que, con suficientes iteraciones, uno puede girar desde el estado inicial ${displaystyle Silenciosrangle }$ al estado de salida deseado ${displaystyle ← }$. El ket inicial está cerca de la ortogonal estatal ${displaystyle ← }$:

${displaystyle langle s' bendicionesrangle ={sqrt {frac {N-1} {N}}}}$

En términos geométricos, el ángulo ${displaystyle theta /2}$ entre ${displaystyle Silenciosrangle }$ y ${displaystyle Silencioso$ es dado por

${displaystyle sin {frac {theta # {2}={frac {1}{sqrt.$

Tenemos que parar cuando el vector estatal pasa cerca ${displaystyle ← }$; después de esto, las iteraciones posteriores giran el vector estatal lejos desde ${displaystyle ← }$, reduciendo la probabilidad de obtener la respuesta correcta. La probabilidad exacta de medir la respuesta correcta es

${displaystyle sin ^{2}left({Big (}r+{frac {1}{2}{Big)}theta right),}$

Donde r es el número (integer) de iteraciones Grover. La primera vez que obtenemos una medición casi óptima es por lo tanto ${displaystyle rapprox pi {sqrt {N}/4}$.

Prueba algebraica de corrección

Para completar el análisis algebraico, necesitamos averiguar qué sucede cuando aplicamos repetidamente ${displaystyle U_{s}U_{omega }$. Una manera natural de hacer esto es mediante el análisis de valor eigenvalue de una matriz. Observe que durante todo el cálculo, el estado del algoritmo es una combinación lineal de ${displaystyle s}$ y ${displaystyle omega }$. Podemos escribir la acción de ${displaystyle U_{s}$ y ${displaystyle U_{omega }$ en el espacio abarcado por ${displaystyle { vidasrangle durableomega rangle}$ como:

${displaystyle U_{s}:a tuberculosisomega rangle +b bendicionesrangle mapsto {begin{bmatrix}abmatrix2/{bqrt {N}}} {bmatrix}{begin{bmatrix}abmatrix}abend{bmatrix}}}}}$

${displaystyle U_{omega }:a sometidaomega rangle +b bendicionesrangle mapsto {begin{bmatrix}abmatrix}abbddbdddcdccH00}$