Algoritmo de generación de laberinto

Algoritmos de generación de laberintos son métodos automatizados para la creación de laberintos.

Este laberinto generado por la versión modificada del algoritmo de Prim, abajo.

Métodos basados en teoría de grafos

Animación del método basado en la teoría del gráfico (búsqueda de profundidad aleatoria)

Se puede generar un laberinto comenzando con una disposición predeterminada de celdas (por lo general, una cuadrícula rectangular, pero son posibles otras disposiciones) con sitios de pared entre ellas. Esta disposición predeterminada se puede considerar como un gráfico conectado con los bordes que representan posibles sitios de pared y los nodos que representan celdas. Entonces, se puede considerar que el propósito del algoritmo de generación de laberintos es crear un subgrafo en el que es difícil encontrar una ruta entre dos nodos particulares.

Si el subgráfico no está conectado, entonces hay regiones del gráfico que se desperdician porque no contribuyen al espacio de búsqueda. Si el gráfico contiene bucles, puede haber varias rutas entre los nodos elegidos. Debido a esto, la generación de laberintos a menudo se considera como la generación de un árbol de expansión aleatorio. Los bucles, que pueden confundir a los ingenuos solucionadores de laberintos, pueden introducirse agregando bordes aleatorios al resultado durante el transcurso del algoritmo.

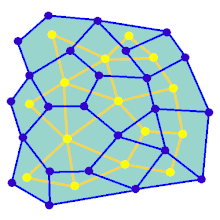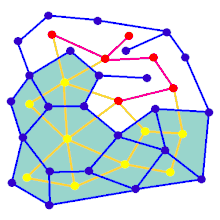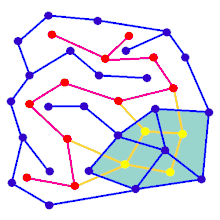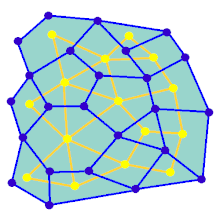
La animación muestra los pasos de generación del laberinto para un gráfico que no está en una cuadrícula rectangular. Primero, la computadora crea un gráfico planar aleatorio G se muestra en azul, y su doble F se muestra en amarillo. En segundo lugar, la computadora recorre F utilizando un algoritmo, como una búsqueda primero en profundidad, coloreando la ruta de rojo. Durante el recorrido, cada vez que un borde rojo se cruza con un borde azul, el borde azul se elimina. Finalmente, cuando se han visitado todos los vértices de F, F se borra y se eliminan dos aristas de G, una para la entrada y otra para la salida.

Búsqueda aleatoria en profundidad

Una animación diferente de un generador mediante búsqueda de profundidad

Este algoritmo, también conocido como "retroceso recursivo" algoritmo, es una versión aleatoria del algoritmo de búsqueda primero en profundidad.

Implementado con frecuencia con una pila, este enfoque es una de las formas más sencillas de generar un laberinto usando una computadora. Considere que el espacio para un laberinto es una gran cuadrícula de celdas (como un gran tablero de ajedrez), cada celda comienza con cuatro paredes. A partir de una celda aleatoria, la computadora selecciona una celda vecina aleatoria que aún no ha sido visitada. La computadora elimina la pared entre las dos celdas y marca la nueva celda como visitada, y la agrega a la pila para facilitar el seguimiento. La computadora continúa este proceso, y una celda que no tiene vecinos no visitados se considera un callejón sin salida. Cuando se encuentra en un callejón sin salida, retrocede por el camino hasta que llega a una celda con un vecino no visitado, continuando la generación del camino al visitar esta nueva celda no visitada (creando un nuevo cruce). Este proceso continúa hasta que se han visitado todas las celdas, lo que hace que la computadora retroceda hasta la celda inicial. Podemos estar seguros de que cada celda es visitada.

Como se indicó anteriormente, este algoritmo implica una recursividad profunda que puede causar problemas de desbordamiento de pila en algunas arquitecturas informáticas. El algoritmo se puede reorganizar en un bucle almacenando información de retroceso en el propio laberinto. Esto también proporciona una forma rápida de mostrar una solución, comenzando en cualquier punto dado y retrocediendo hasta el principio.

Bias de paso horizontal

Los laberintos generados con una búsqueda en profundidad tienen un factor de ramificación bajo y contienen muchos pasillos largos, porque el algoritmo explora lo más lejos posible a lo largo de cada rama antes de retroceder.

Implementación recursiva

El algoritmo de búsqueda primero en profundidad de la generación de laberintos se implementa con frecuencia mediante el retroceso. Esto se puede describir con la siguiente rutina recursiva:

1. Dado una celda actual como parámetro
2. Marcar la celda actual visitada
3. Mientras que la célula actual tiene células vecinas no visibles
   1. Elige a uno de los vecinos no visitados
   2. Quitar la pared entre la celda actual y la celda elegida
   3. Invocar la rutina recursivamente para la célula elegida

que se invoca una vez para cualquier celda inicial en el área.

Implementación iterativa

Una desventaja del primer enfoque es una gran profundidad de recursividad: en el peor de los casos, es posible que la rutina deba repetirse en cada celda del área que se está procesando, lo que puede exceder la profundidad máxima de la pila de recursividad en muchos entornos. Como solución, se puede implementar el mismo método de retroceso con una pila explícita, que generalmente se permite que crezca mucho más sin daño.

1. Elija la celda inicial, marque la visita y presione la pila
2. Mientras que la pila no está vacía
   1. Abre una celda de la pila y haz que sea una célula actual
   2. Si la celda actual tiene vecinos que no han sido visitados
      1. Empuja la celda actual a la pila
      2. Elige a uno de los vecinos no visitados
      3. Quitar la pared entre la celda actual y la celda elegida
      4. Marcar la celda elegida como visitada y empujarla a la pila

Algoritmo de Kruskal aleatorio

Este algoritmo es una versión aleatoria del algoritmo de Kruskal.

1. Crear una lista de todas las paredes, y crear un conjunto para cada célula, cada uno conteniendo sólo una célula.
2. Para cada pared, en algún orden al azar:
   1. Si las células divididas por esta pared pertenecen a conjuntos distintos:
      1. Quita la pared actual.
      2. Únete a los conjuntos de las células antes divididas.

Hay varias estructuras de datos que se pueden utilizar para modelar los conjuntos de células. Una implementación eficiente usando una estructura de datos de conjunto disyuntiva puede realizar cada unión y encontrar operación en dos conjuntos en tiempo amortizado casi constante (específicamente, O()α α ()V)){displaystyle O(alpha (V)} tiempo; <math alttext="{displaystyle alpha (x)α α ()x).5{displaystyle alpha (x)<img alt="alpha (x) para cualquier valor plausible x{displaystyle x}), por lo que el tiempo de funcionamiento de este algoritmo es esencialmente proporcional al número de paredes disponibles para el laberinto.

Poco importa si la lista de muros es inicialmente aleatoria o si un muro se elige aleatoriamente de una lista no aleatoria, cualquiera de las dos formas es igual de fácil de codificar.

Debido a que el efecto de este algoritmo es producir un árbol de expansión mínimo a partir de un gráfico con bordes igualmente ponderados, tiende a producir patrones regulares que son bastante fáciles de resolver.

Algoritmo de Prim aleatorio

Este algoritmo es una versión aleatoria del algoritmo de Prim.

1. Comience con una rejilla llena de paredes.
2. Escoge una celda, marca como parte del laberinto. Añadir las paredes de la celda a la lista de la pared.
3. Mientras hay paredes en la lista:
   1. Escoge una pared al azar de la lista. Si sólo una de las células que divide la pared es visitada, entonces:
      1. Haz de la pared un pasaje y marca la célula no vista como parte del laberinto.
      2. Añadir las paredes vecinas de la celda a la lista de la pared.
   2. Quitar la pared de la lista.

Tenga en cuenta que la simple ejecución de Prim's clásico en un gráfico con pesos de borde aleatorios crearía laberintos estilísticamente idénticos a Kruskal's, porque ambos son algoritmos de árbol de expansión mínimo. En cambio, este algoritmo introduce una variación estilística porque los bordes más cercanos al punto de inicio tienen un peso efectivo más bajo.

Versión modificada

Aunque el algoritmo clásico de Prim mantiene una lista de bordes, para la generación de laberintos podríamos mantener una lista de celdas adyacentes. Si la celda elegida al azar tiene varios bordes que la conectan con el laberinto existente, seleccione uno de estos bordes al azar. Esto tenderá a ramificarse un poco más que la versión anterior basada en el borde.

Versión simplificada

El algoritmo se puede simplificar aún más seleccionando aleatoriamente las celdas vecinas a las celdas ya visitadas, en lugar de realizar un seguimiento de los pesos de todas las celdas o bordes.

Por lo general, será relativamente fácil encontrar el camino a la celda inicial, pero difícil encontrar el camino en cualquier otro lugar.

Algoritmo de Wilson

Animación de generación de laberinto usando el algoritmo de Wilson (gray representa un paseo aleatorio continuo). Una vez construido el laberinto se resuelve utilizando profundidad primera búsqueda

Todos los algoritmos anteriores tienen sesgos de varios tipos: la búsqueda en profundidad está sesgada hacia corredores largos, mientras que los algoritmos de Kruskal/Prim están sesgados hacia muchos callejones sin salida cortos. El algoritmo de Wilson, por otro lado, genera una muestra imparcial a partir de la distribución uniforme en todos los laberintos, utilizando caminatas aleatorias borradas en bucle.

Comenzamos el algoritmo inicializando el laberinto con una celda elegida arbitrariamente. Luego, comenzamos en una nueva celda elegida arbitrariamente y realizamos una caminata aleatoria hasta que llegamos a una celda que ya está en el laberinto; sin embargo, si en algún punto la caminata aleatoria llega a su propio camino, formando un bucle, borramos el bucle del camino. antes de continuar. Cuando el camino llega al laberinto, lo agregamos al laberinto. Luego realizamos otra caminata aleatoria borrada en bucle desde otra celda de inicio arbitraria, repitiendo hasta que se hayan llenado todas las celdas.

Este procedimiento sigue siendo imparcial, independientemente del método que utilicemos para elegir arbitrariamente las celdas iniciales. Por lo tanto, siempre podríamos elegir la primera celda vacía en (digamos) orden de izquierda a derecha y de arriba a abajo para simplificar.

Algoritmo Aldous-Broder

El algoritmo de Aldous-Broder también produce árboles de expansión uniformes. Sin embargo, es uno de los algoritmos de laberinto menos eficientes.

1. Escoja una célula aleatoria como la célula actual y marquelo como se visita.
2. Mientras hay células no visibles:
   1. Escoge un vecino al azar.
   2. Si el vecino elegido no ha sido visitado:
      1. Quitar la pared entre la celda actual y el vecino elegido.
      2. Marque al vecino elegido como visitado.
   3. Haga al vecino elegido la celda actual.

Método de división recursiva

Ilustración de la División Recursiva

cámara original	división por dos paredes	agujeros en paredes	continuar subdividiendo...	terminado
paso 1	paso 2	paso 3	paso 4	paso 5

Los laberintos se pueden crear con división recursiva, un algoritmo que funciona de la siguiente manera: comience con el espacio del laberinto sin paredes. Llama a esto una cámara. Divida la cámara con una pared colocada al azar (o varias paredes) donde cada pared contenga una abertura de pasaje colocada al azar dentro de ella. Luego repita recursivamente el proceso en las subcámaras hasta que todas las cámaras tengan el tamaño mínimo. Este método da como resultado laberintos con largas paredes rectas que cruzan su espacio, lo que facilita ver qué áreas evitar.

Por ejemplo, en un laberinto rectangular, construya en puntos aleatorios dos paredes que sean perpendiculares entre sí. Estas dos paredes dividen la cámara grande en cuatro cámaras más pequeñas separadas por cuatro paredes. Elija tres de las cuatro paredes al azar y abra un agujero de una celda de ancho en un punto aleatorio en cada una de las tres. Continúe de esta manera recursivamente, hasta que cada cámara tenga un ancho de una celda en cualquiera de las dos direcciones.

Algoritmos simples

Versión 3D del algoritmo de Prim. Las capas verticales se etiquetan 1 a 4 de abajo a arriba. Las escaleras arriba se indican con "/"; escaleras abajo con "", y escaleras arriba y abajo con "x". El código fuente se incluye con la descripción de la imagen.

Existen otros algoritmos que solo requieren suficiente memoria para almacenar una línea de un laberinto 2D o un plano de un laberinto 3D. El algoritmo de Eller evita los bucles al almacenar qué celdas de la línea actual están conectadas a través de las celdas de las líneas anteriores, y nunca elimina las paredes entre dos celdas ya conectadas. El algoritmo Sidewinder comienza con un pasaje abierto a lo largo de toda la fila superior y las filas subsiguientes consisten en pasajes horizontales más cortos con una conexión con el pasaje anterior. El algoritmo Sidewinder es trivial de resolver de abajo hacia arriba porque no tiene callejones sin salida hacia arriba. Dado un ancho inicial, ambos algoritmos crean laberintos perfectos de altura ilimitada.

La mayoría de los algoritmos de generación de laberintos requieren mantener relaciones entre las celdas dentro de él, para garantizar que el resultado final sea solucionable. Sin embargo, se pueden generar laberintos válidos simplemente conectados centrándose en cada celda de forma independiente. Un laberinto de árbol binario es un laberinto ortogonal estándar en el que cada celda siempre tiene un pasaje que conduce hacia arriba o hacia la izquierda, pero nunca ambos. Para crear un laberinto de árbol binario, para cada celda, lanza una moneda para decidir si agregar un pasaje hacia arriba o hacia la izquierda. Elija siempre la misma dirección para las celdas en el límite, y el resultado final será un laberinto válido simplemente conectado que parece un árbol binario, con la esquina superior izquierda como raíz. Al igual que con Sidewinder, el laberinto del árbol binario no tiene callejones sin salida en las direcciones del sesgo.

Maze generado en Commodore 64 BASIC, utilizando el código 10 PRINT CHR$(205.5+RND(1));: GOTO 10

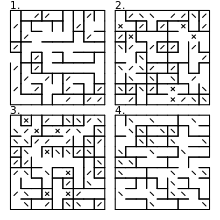
Una forma relacionada de lanzar una moneda al aire para cada celda es crear una imagen utilizando una combinación aleatoria de caracteres de barra inclinada y barra invertida. Esto no genera un laberinto simplemente conectado válido, sino una selección de bucles cerrados y pasajes unicursales. El manual del Commodore 64 presenta un programa BÁSICO que utiliza este algoritmo, utilizando en su lugar caracteres gráficos de líneas diagonales PETSCII para una apariencia gráfica más suave.

Algoritmos de autómatas celulares

Se pueden usar ciertos tipos de autómatas celulares para generar laberintos. Dos autómatas celulares conocidos, Maze y Mazectric, tienen cadenas de reglas B3/S12345 y B3/S1234. En el primero, esto significa que las células sobreviven de una generación a la siguiente si tienen al menos uno y como máximo cinco vecinos. En este último, esto significa que las células sobreviven si tienen de uno a cuatro vecinos. Si una célula tiene exactamente tres vecinos, nace. Es similar al Juego de la vida de Conway en que los patrones que no tienen una célula viva adyacente a 1, 4 o 5 otras células vivas en cualquier generación se comportarán de manera idéntica. Sin embargo, para patrones grandes, se comporta de manera muy diferente a Life.

Para un patrón de inicio aleatorio, estos autómatas celulares generadores de laberintos evolucionarán a laberintos complejos con paredes bien definidas que delimitan pasillos. Mazecetric, que tiene la regla B3/S1234, tiene tendencia a generar pasillos más largos y rectos en comparación con Maze, con la regla B3/S12345. Dado que estas reglas de autómatas celulares son deterministas, cada laberinto generado está determinado únicamente por su patrón de inicio aleatorio. Este es un inconveniente significativo ya que los laberintos tienden a ser relativamente predecibles.

Al igual que algunos de los métodos basados en la teoría de grafos descritos anteriormente, estos autómatas celulares suelen generar laberintos a partir de un único patrón inicial; por lo tanto, generalmente será relativamente fácil encontrar el camino a la celda inicial, pero más difícil encontrar el camino en cualquier otro lugar.