Algoritmo de búsqueda binaria

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Buscar algoritmo encontrar la posición de un valor objetivo dentro de un array ordenados

En informática, búsqueda binaria, también conocida como búsqueda de medio intervalo, búsqueda logarítmica o corte binario, es un algoritmo de búsqueda que encuentra la posición de un valor objetivo dentro de una matriz ordenada. La búsqueda binaria compara el valor objetivo con el elemento central de la matriz. Si no son iguales, se elimina la mitad en la que el objetivo no puede estar y la búsqueda continúa en la mitad restante, tomando nuevamente el elemento central para compararlo con el valor objetivo, y repitiendo esto hasta encontrar el valor objetivo. Si la búsqueda termina con la mitad restante vacía, el objetivo no está en la matriz.

La búsqueda binaria funciona en el tiempo logarítmico en el peor de los casos, haciendo $O(log n)$ comparaciones, donde $n$ es el número de elementos en el array. La búsqueda binaria es más rápida que la búsqueda lineal excepto para pequeños arrays. Sin embargo, el array debe ser clasificado primero para poder aplicar la búsqueda binaria. Hay estructuras especializadas de datos diseñadas para la búsqueda rápida, como tablas de hash, que pueden ser buscadas más eficientemente que la búsqueda binaria. Sin embargo, la búsqueda binaria se puede utilizar para resolver una gama más amplia de problemas, como encontrar el elemento más próximo o más grande en el array relativo al objetivo, incluso si está ausente del array.

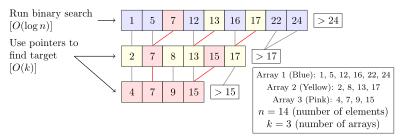
Existen numerosas variaciones de la búsqueda binaria. En particular, la cascada fraccionaria acelera las búsquedas binarias del mismo valor en varias matrices. La cascada fraccional resuelve de manera eficiente una serie de problemas de búsqueda en geometría computacional y en muchos otros campos. La búsqueda exponencial extiende la búsqueda binaria a listas ilimitadas. Las estructuras de datos del árbol de búsqueda binaria y del árbol B se basan en la búsqueda binaria.

Algoritmo

La búsqueda binaria funciona en matrices ordenadas. La búsqueda binaria comienza comparando un elemento en el medio de la matriz con el valor objetivo. Si el valor de destino coincide con el elemento, se devuelve su posición en la matriz. Si el valor objetivo es menor que el elemento, la búsqueda continúa en la mitad inferior de la matriz. Si el valor objetivo es mayor que el elemento, la búsqueda continúa en la mitad superior de la matriz. Al hacer esto, el algoritmo elimina la mitad en la que el valor objetivo no puede estar en cada iteración.

Procedimiento

Dado un array $A$ de $n$ elementos con valores o registros ${displaystyle A_{0},A_{1},A_{2},ldotsA_{n-1}}$ Entendido. ${displaystyle A_{0}leq A_{1}leq A_{2}leq cdots leq A_{n-1}}$ , y valor objetivo $T$ , la siguiente subrutina utiliza búsqueda binaria para encontrar el índice de $T$ dentro $A$ .

Set $L$ a $0$ y $R$ a $n-1$ .
Si $R}" xmlns="http://www.w3.org/1998/Math/MathML">L■R{displaystyle L títuloR}R}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/145ce1d631364a50d19ac5264c7dc09d4e158b0a" style="vertical-align: -0.338ex; width:6.445ex; height:2.176ex;"/>$ , la búsqueda termina como infructuosa.
Set $m$ (la posición del elemento medio) al suelo ${displaystyle {frac {L+R}{2}}}$ , que es el mayor entero menos o igual a ${displaystyle {frac {L+R}{2}}}$ .
Si $<math alttext="{displaystyle A_{m}Am.T{displaystyle A_{m} madeT}<img alt="{displaystyle A_{m}$ , set $L$ a $m+1$ e ir al paso 2.
Si $T}" xmlns="http://www.w3.org/1998/Math/MathML">Am■T{displaystyle A_{m} T}T}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/d8f333a047adf793929566dda96ffdf4493cf3b7" style="vertical-align: -0.671ex; width:8.153ex; height:2.509ex;"/>$ , set $R$ a $m-1$ e ir al paso 2.
Ahora ${displaystyle A_{m}=T}$ , la búsqueda se hace; retorno $m$ .

Este procedimiento iterativo mantiene el seguimiento de los límites de búsqueda con las dos variables $L$ y $R$ . El procedimiento puede expresarse en pseudocódigo de la siguiente manera, donde los nombres y tipos variables permanecen iguales a los anteriores, floor es la función del suelo, y unsuccessful se refiere a un valor específico que transmite el fracaso de la búsqueda.

binaria-búsqueda

función binario_search(A, n, T) esL:= 0
R:= n - 1
 mientras L ≤ R dom:= piso(L + R) / 2)
 si A[m] entoncesL:= m + 1
 si A[m] T entoncesR:= m - 1
 más:
 retorno m
 retorno sin éxito

Alternativamente, el algoritmo puede tomar el techo de ${displaystyle {frac {L+R}{2}}}$ . Esto puede cambiar el resultado si el valor objetivo aparece más de una vez en el array.

Procedimiento alternativo

En el procedimiento anterior, el algoritmo comprueba si el elemento medio ( $m$ ) es igual al objetivo ( $T$ En cada iteración. Algunas implementaciones dejan este cheque durante cada iteración. El algoritmo realizaría este cheque sólo cuando un elemento queda (cuando ${displaystyle L=R}$ ). Esto resulta en un bucle de comparación más rápido, ya que una comparación se elimina por iteración, mientras que sólo requiere una iteración más en promedio.

Hermann Bottenbruch publicó la primera implementación para omitir esta verificación en 1962.

Set $L$ a $0$ y $R$ a $n-1$ .
Mientras tanto Lل ل R{displaystyle Lneq R} ${displaystyle Lneq R}$ ,
1. Set $m$ (la posición del elemento medio) al techo ${displaystyle {frac {L+R}{2}}}$ , que es el menor entero mayor o igual a ${displaystyle {frac {L+R}{2}}}$ .
2. Si $T}" xmlns="http://www.w3.org/1998/Math/MathML">Am■T{displaystyle A_{m} T}T}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/d8f333a047adf793929566dda96ffdf4493cf3b7" style="vertical-align: -0.671ex; width:8.153ex; height:2.509ex;"/>$ , set $R$ a $m-1$ .
3. Else, ${displaystyle A_{m}leq T}$ ; set $L$ a $m$ .
Ahora ${displaystyle L=R}$ , la búsqueda se hace. Si ${displaystyle A_{L}=T}$ , regreso $L$ . De lo contrario, la búsqueda termina como infructuosa.

Donde ceil es la función de techo, el pseudocódigo para esta versión es:

función binario_search_alternative(A, n, T) esL:= 0
R:= n - 1
 mientras ¡L! R dom:= ceil(L + R) / 2)
 si A[m] T entoncesR:= m - 1
 más:
L:= m
 si A[L] = T entonces retorno L
 retorno sin éxito

Elementos duplicados

El procedimiento puede devolver cualquier índice cuyo elemento es igual al valor objetivo, incluso si hay elementos duplicados en el array. Por ejemplo, si el array a buscar fue ${displaystyle [1,2,3,4,4,5,6,7]}$ y el objetivo era $4$ , entonces sería correcto que el algoritmo devuelva el elemento 4o (index 3) o 5o (index 4). El procedimiento ordinario devolvería el cuarto elemento (índice 3) en este caso. No siempre devuelve el primer duplicado (considerador) ${displaystyle [1,2,4,4,4,5,6,7]}$ que todavía devuelve el cuarto elemento). Sin embargo, a veces es necesario encontrar el elemento más izquierdo o el elemento más adecuado para un valor objetivo que se duplica en el array. En el ejemplo anterior, el cuarto elemento es el elemento más izquierdo del valor 4, mientras que el quinto elemento es el elemento más derecho del valor 4. El procedimiento alternativo anterior siempre devolverá el índice del elemento más adecuado si existe tal elemento.

Procedimiento para encontrar el elemento más a la izquierda

Para encontrar el elemento más a la izquierda, se puede usar el siguiente procedimiento:

Set $L$ a $0$ y $R$ a $n$ .
Mientras tanto <math alttext="{displaystyle LL.R{displaystyle L<img alt="{displaystyle L,
1. Set $m$ (la posición del elemento medio) al suelo ${displaystyle {frac {L+R}{2}}}$ , que es el mayor entero menos o igual a ${displaystyle {frac {L+R}{2}}}$ .
2. Si $<math alttext="{displaystyle A_{m}Am.T{displaystyle A_{m} madeT}<img alt="{displaystyle A_{m}$ , set $L$ a $m+1$ .
3. Else, ${displaystyle A_{m}geq T}$ ; set $R$ a $m$ .
Regreso $L$ .

Si $<math alttext="{displaystyle LL.n{displaystyle ¡No! <img alt="{displaystyle L$ y ${displaystyle A_{L}=T}$ , entonces $A_{L}$ es el elemento más izquierdo que igual $T$ . Incluso si $T$ no está en el array, $L$ es el rango de $T$ en el array, o el número de elementos en el array que son menos que $T$ .

Donde floor es la función de suelo, el pseudocódigo para esta versión es:

función binario_search_leftmost(A, n, T):
L:= 0
R:= n
 mientras L.
m:= piso(L + R) / 2)
 si A[m]
L:= m + 1
 más:
R:= m
 retorno L

Procedimiento para encontrar el elemento más a la derecha

Para encontrar el elemento más a la derecha, se puede usar el siguiente procedimiento:

Set $L$ a $0$ y $R$ a $n$ .
Mientras tanto <math alttext="{displaystyle LL.R{displaystyle L<img alt="{displaystyle L,
1. Set $m$ (la posición del elemento medio) al suelo ${displaystyle {frac {L+R}{2}}}$ , que es el mayor entero menos o igual a ${displaystyle {frac {L+R}{2}}}$ .
2. Si $T}" xmlns="http://www.w3.org/1998/Math/MathML">Am■T{displaystyle A_{m} T}T}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/d8f333a047adf793929566dda96ffdf4493cf3b7" style="vertical-align: -0.671ex; width:8.153ex; height:2.509ex;"/>$ , set $R$ a $m$ .
3. Else, ${displaystyle A_{m}leq T}$ ; set $L$ a $m+1$ .
Regreso ${displaystyle R-1}$ .

Si $0}" xmlns="http://www.w3.org/1998/Math/MathML">R■0{displaystyle R =0} 0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/57914127d03a5cea02c60a32cfbb22f34904f00d" style="vertical-align: -0.338ex; width:6.025ex; height:2.176ex;"/>$ y ${displaystyle A_{R-1}=T}$ , entonces ${displaystyle A_{R-1}}$ es el elemento más adecuado que igual $T$ . Incluso si $T$ no está en el array, ${displaystyle n-R}$ es el número de elementos en la matriz que son mayores que $T$ .

Donde floor es la función de suelo, el pseudocódigo para esta versión es:

función binario_search_rightmost(A, n, T):
L:= 0
R:= n
 mientras L.
m:= piso(L + R) / 2)
 si A[m] T:
R:= m
 más:
L:= m + 1
 retorno R - 1

Coincidencias aproximadas

La búsqueda binaria se puede adaptar para calcular coincidencias aproximadas. En el ejemplo anterior, se muestra el rango, predecesor, sucesor y vecino más cercano para el valor objetivo

5

, que no está en el array.

El procedimiento anterior solo realiza coincidencias exactas, encontrando la posición de un valor objetivo. Sin embargo, es trivial extender la búsqueda binaria para realizar coincidencias aproximadas porque la búsqueda binaria opera en matrices ordenadas. Por ejemplo, la búsqueda binaria se puede utilizar para calcular, para un valor dado, su rango (el número de elementos más pequeños), el predecesor (el siguiente elemento más pequeño), el sucesor (el siguiente elemento más grande) y el vecino más cercano. Las consultas de rango que buscan el número de elementos entre dos valores se pueden realizar con dos consultas de rango.

Se pueden realizar consultas con el procedimiento para encontrar el elemento más izquierdo. Número de elementos menos que el valor objetivo es devuelto por el procedimiento.
Las consultas previas pueden realizarse con consultas de rango. Si el rango del valor objetivo es $r$ , su predecesor es $r-1$ .
Para las consultas posteriores, se puede utilizar el procedimiento para encontrar el elemento más adecuado. Si el resultado de ejecutar el procedimiento para el valor objetivo es $r$ , entonces el sucesor del valor objetivo es $r+1$ .
El vecino más cercano del valor objetivo es ya sea su predecesor o sucesor, cualquiera que sea más cercano.
Las consultas de rango también son directas. Una vez que se conocen las filas de los dos valores, el número de elementos mayor o igual al primer valor y menos que el segundo es la diferencia de las dos categorías. Este recuento puede ser ajustado hacia arriba o hacia abajo por uno según si los puntos finales del rango deben considerarse parte del rango y si el array contiene entradas que coincidan con esos puntos finales.

Rendimiento

Un árbol que representa la búsqueda binaria. El array que se está buscando aquí es

{displaystyle [20,30,40,50,80,90,100]}

, y el valor objetivo es

{displaystyle 40}

El peor caso se alcanza cuando la búsqueda alcanza el nivel más profundo del árbol, mientras que el mejor caso se alcanza cuando el valor objetivo es el elemento medio.

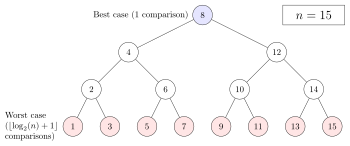
En términos de la cantidad de comparaciones, el rendimiento de la búsqueda binaria se puede analizar al ver la ejecución del procedimiento en un árbol binario. El nodo raíz del árbol es el elemento central de la matriz. El elemento medio de la mitad inferior es el nodo secundario izquierdo de la raíz, y el elemento medio de la mitad superior es el nodo secundario derecho de la raíz. El resto del árbol está construido de manera similar. A partir del nodo raíz, se recorren los subárboles izquierdo o derecho dependiendo de si el valor objetivo es menor o mayor que el nodo en consideración.

En el peor de los casos, la búsqueda binaria hace ${textstyle lfloor log _{2}(n)+1rfloor }$ iteraciones del bucle de comparación, donde el ${textstyle lfloor rfloor }$ notación denota la función del suelo que produce el mayor entero menos o igual al argumento, y ${textstyle log _{2}}$ es el logaritmo binario. Esto se debe a que el peor caso es alcanzado cuando la búsqueda alcanza el nivel más profundo del árbol, y siempre hay ${textstyle lfloor log _{2}(n)+1rfloor }$ niveles en el árbol para cualquier búsqueda binaria.

El peor caso también puede ser alcanzado cuando el elemento objetivo no está en el array. Si ${textstyle n}$ es menos que un poder de dos, entonces este es siempre el caso. De lo contrario, la búsqueda puede realizar ${textstyle lfloor log _{2}(n)+1rfloor }$ iteraciones si la búsqueda alcanza el nivel más profundo del árbol. Sin embargo, puede hacer ${textstyle lfloor log _{2}(n)rfloor }$ iteraciones, que es menos que el peor caso, si la búsqueda termina en el segundo nivel más profundo del árbol.

En promedio, asumiendo que cada elemento es igualmente probable que sea buscado, la búsqueda binaria hace ${displaystyle lfloor log _{2}(n)rfloor +1-(2^{lfloor log _{2}(n)rfloor +1}-lfloor log _{2}(n)rfloor -2)/n}$ iteraciones cuando el elemento objetivo está en el array. Esto es aproximadamente igual a ${displaystyle log _{2}(n)-1}$ iteraciones. Cuando el elemento objetivo no está en el array, la búsqueda binaria hace ${displaystyle lfloor log _{2}(n)rfloor +2-2^{lfloor log _{2}(n)rfloor +1}/(n+1)}$ iteraciones en promedio, asumiendo que el rango entre y los elementos externos es igualmente probable que se busque.

En el mejor de los casos, cuando el valor objetivo es el elemento central de la matriz, su posición se devuelve después de una iteración.

En términos de iteraciones, ningún algoritmo de búsqueda que funcione solo comparando elementos puede exhibir un mejor desempeño promedio y en el peor de los casos que la búsqueda binaria. El árbol de comparación que representa la búsqueda binaria tiene la menor cantidad de niveles posible ya que cada nivel por encima del nivel más bajo del árbol se llena por completo. De lo contrario, el algoritmo de búsqueda puede eliminar pocos elementos en una iteración, aumentando el número de iteraciones requeridas en el promedio y en el peor de los casos. Este es el caso de otros algoritmos de búsqueda basados en comparaciones, ya que si bien pueden funcionar más rápido en algunos valores objetivo, el rendimiento promedio sobre todos los elementos es peor que la búsqueda binaria. Al dividir el arreglo por la mitad, la búsqueda binaria asegura que el tamaño de ambos subarreglos sea lo más similar posible.

Complejidad del espacio

La búsqueda binaria requiere tres punteros a elementos, que pueden ser índices de array o punteros a lugares de memoria, independientemente del tamaño de la matriz. Por lo tanto, la complejidad espacial de la búsqueda binaria es $O(1)$ en la palabra modelo RAM de computación.

Derivación del caso promedio

El número promedio de iteraciones realizadas por búsqueda binaria depende de la probabilidad de que cada elemento sea buscado. El caso promedio es diferente para búsquedas exitosas y búsquedas sin éxito. Se supone que cada elemento es igualmente probable que sea buscado por búsquedas exitosas. Para búsquedas infructuosas, se supone que los intervalos entre elementos externos y entre ellos son igualmente propensos a ser buscados. El caso promedio de búsquedas exitosas es el número de iteraciones requeridas para buscar cada elemento exactamente una vez, divididas por $n$ , el número de elementos. El caso promedio de búsquedas no exitosas es el número de iteraciones requeridas para buscar un elemento dentro de cada intervalo exactamente una vez, divididas por el $n+1$ intervalos.

Búsquedas exitosas

En la representación binaria del árbol, una búsqueda exitosa puede ser representada por un camino desde la raíz hasta el nodo objetivo, llamado un ruta interna. La longitud de un camino es el número de bordes (conexiones entre nodos) que el camino pasa a través. El número de iteraciones realizadas por una búsqueda, dado que el camino correspondiente tiene longitud $l$ , es ${displaystyle l+1}$ Contando la iteración inicial. El longitud de la ruta interna es la suma de las longitudes de todos los caminos interiores únicos. Puesto que sólo hay un camino de la raíz a cualquier nodo único, cada camino interno representa una búsqueda de un elemento específico. Si hay $n$ elementos, que es un entero positivo, y la longitud del camino interno es $I(n)$ , entonces el número promedio de iteraciones para una búsqueda exitosa ${displaystyle T(n)=1+{frac {I(n)}{n}}}$ , con la única iteración agregada para contar la iteración inicial.

Puesto que la búsqueda binaria es el algoritmo óptimo para la búsqueda con comparaciones, este problema se reduce a calcular la longitud mínima de la ruta interna de todos los árboles binarios con $n$ nodos, que es igual a:

${displaystyle I(n)=sum _{k=1}^{n}leftlfloor log _{2}(k)rightrfloor }$

Por ejemplo, en una matriz de 7 elementos, la raíz requiere una iteración, los dos elementos debajo de la raíz requieren dos iteraciones y los cuatro elementos debajo requieren tres iteraciones. En este caso, la longitud del camino interno es:

${displaystyle sum _{k=1}^{7}leftlfloor log _{2}(k)rightrfloor =0+2(1)+4(2)=2+8=10}$

El promedio de iteraciones sería ${displaystyle 1+{frac {10}{7}}=2{frac {3}{7}}}$ basado en la ecuación para el caso promedio. La suma para $I(n)$ se puede simplificar para:

${displaystyle I(n)=sum _{k=1}^{n}leftlfloor log _{2}(k)rightrfloor =(n+1)leftlfloor log _{2}(n+1)rightrfloor -2^{leftlfloor log _{2}(n+1)rightrfloor +1}+2}$

Sustituir la ecuación para $I(n)$ en la ecuación para $T(n)$ :

${displaystyle T(n)=1+{frac {(n+1)leftlfloor log _{2}(n+1)rightrfloor -2^{leftlfloor log _{2}(n+1)rightrfloor +1}+2}{n}}=lfloor log _{2}(n)rfloor +1-(2^{lfloor log _{2}(n)rfloor +1}-lfloor log _{2}(n)rfloor -2)/n}$

Para entero $n$ , esto es equivalente a la ecuación para el caso promedio en una búsqueda exitosa especificada anteriormente.

Búsquedas fallidas

Las búsquedas infructuosas pueden ser representadas aumentando el árbol con nodos externos, que forma un árbol binario extendido. Si un nodo interno, o un nodo presente en el árbol, tiene menos de dos nodos infantiles, se añaden nodos adicionales, llamados ganglios externos, de modo que cada nodo interno tenga dos hijos. Al hacerlo, una búsqueda infructuosa puede ser representada como un camino hacia un nodo externo, cuyo padre es el único elemento que permanece durante la última iteración. An vía externa es un camino desde la raíz a un nodo externo. El longitud de la ruta externa es la suma de las longitudes de todos los caminos externos únicos. Si hay $n$ elementos, que es un entero positivo, y la longitud de la trayectoria externa es $E(n)$ , entonces el número promedio de iteraciones para una búsqueda sin éxito ${displaystyle T'(n)={frac {E(n)}{n+1}}}$ , con la única iteración agregada para contar la iteración inicial. La longitud de la trayectoria externa se divide por $n+1$ en lugar de $n$ porque hay $n+1$ caminos externos, representando los intervalos entre y fuera de los elementos del array.

Este problema se puede reducir de forma similar a la determinación de la duración mínima de la ruta externa de todos los árboles binarios con $n$ nodos. Para todos los árboles binarios, la longitud de la ruta externa es igual a la longitud de la ruta interna más $2n$ . Sustituir la ecuación para $I(n)$ :

${displaystyle E(n)=I(n)+2n=left[(n+1)leftlfloor log _{2}(n+1)rightrfloor -2^{leftlfloor log _{2}(n+1)rightrfloor +1}+2right]+2n=(n+1)(lfloor log _{2}(n)rfloor +2)-2^{lfloor log _{2}(n)rfloor +1}}$

Sustituir la ecuación para $E(n)$ en la ecuación para ${displaystyle T'(n)}$ , el caso promedio de búsquedas no exitosas se puede determinar:

${displaystyle T'(n)={frac {(n+1)(lfloor log _{2}(n)rfloor +2)-2^{lfloor log _{2}(n)rfloor +1}}{(n+1)}}=lfloor log _{2}(n)rfloor +2-2^{lfloor log _{2}(n)rfloor +1}/(n+1)}$

Realización del procedimiento alternativo

Cada iteración del procedimiento de búsqueda binaria definido anteriormente hace una o dos comparaciones, comprobando si el elemento medio es igual al objetivo en cada iteración. Asumiendo que cada elemento es igualmente probable que sea buscado, cada iteración hace 1,5 comparaciones en promedio. Una variación del algoritmo comprueba si el elemento medio es igual al objetivo al final de la búsqueda. En promedio, esto elimina la mitad de una comparación de cada iteración. Esto corta ligeramente el tiempo tomado por iteración en la mayoría de las computadoras. Sin embargo, garantiza que la búsqueda tome el número máximo de iteraciones, en promedio añadiendo una iteración a la búsqueda. Porque el bucle de comparación se realiza sólo ${textstyle lfloor log _{2}(n)+1rfloor }$ tiempos en el peor de los casos, el ligero aumento de eficiencia por iteración no compensa la iteración extra para todos pero muy grande ${textstyle n}$ .

Tiempo de ejecución y uso de caché

Al analizar el rendimiento de la búsqueda binaria, otra consideración es el tiempo necesario para comparar dos elementos. Para números enteros y cadenas, el tiempo requerido aumenta linealmente a medida que aumenta la longitud de codificación (generalmente el número de bits) de los elementos. Por ejemplo, comparar un par de enteros sin signo de 64 bits requeriría comparar hasta el doble de bits que comparar un par de enteros sin signo de 32 bits. El peor de los casos se logra cuando los números enteros son iguales. Esto puede ser significativo cuando las longitudes de codificación de los elementos son grandes, como con tipos de enteros grandes o cadenas largas, lo que hace que la comparación de elementos sea costosa. Además, comparar valores de punto flotante (la representación digital más común de números reales) suele ser más costoso que comparar números enteros o cadenas cortas.

En la mayoría de las arquitecturas informáticas, el procesador tiene una caché de hardware separada de la RAM. Dado que están ubicados dentro del propio procesador, los cachés son mucho más rápidos de acceder, pero generalmente almacenan muchos menos datos que la RAM. Por lo tanto, la mayoría de los procesadores almacenan ubicaciones de memoria a las que se ha accedido recientemente, junto con ubicaciones de memoria cercanas. Por ejemplo, cuando se accede a un elemento de matriz, el elemento en sí puede almacenarse junto con los elementos que están almacenados cerca de él en la RAM, lo que hace que sea más rápido acceder secuencialmente a los elementos de matriz que tienen un índice cercano entre sí (localidad de referencia). En una matriz ordenada, la búsqueda binaria puede saltar a ubicaciones de memoria distantes si la matriz es grande, a diferencia de los algoritmos (como la búsqueda lineal y el sondeo lineal en tablas hash) que acceden a los elementos en secuencia. Esto aumenta ligeramente el tiempo de ejecución de la búsqueda binaria de matrices grandes en la mayoría de los sistemas.

Búsqueda binaria versus otros esquemas

Los arrays clasificados con búsqueda binaria son una solución muy ineficiente cuando las operaciones de inserción y eliminación están entrelazadas con recuperación, tomando ${textstyle O(n)}$ tiempo para cada operación. Además, los arrays ordenados pueden complicar el uso de la memoria especialmente cuando los elementos se insertan a menudo en el array. Hay otras estructuras de datos que apoyan una inserción y eliminación mucho más eficientes. La búsqueda binaria se puede utilizar para realizar exactamente igualación y fijar la membresía (determinando si un valor objetivo está en una colección de valores). Hay estructuras de datos que soportan una coincidencia más rápida y establecer la membresía. Sin embargo, a diferencia de muchos otros esquemas de búsqueda, la búsqueda binaria se puede utilizar para una coincidencia aproximada eficiente, generalmente realizando tales coincidencias en ${textstyle O(log n)}$ tiempo independientemente del tipo o estructura de los valores mismos. Además, hay algunas operaciones, como encontrar el elemento más pequeño y más grande, que se puede realizar eficientemente en un array ordenados.

Búsqueda lineal

La búsqueda lineal es un algoritmo de búsqueda simple que verifica cada registro hasta que encuentre el valor objetivo. La búsqueda lineal se puede realizar en una lista conectada, lo que permite una inserción y eliminación más rápidas que un array. La búsqueda binaria es más rápida que la búsqueda lineal de arrays ordenados excepto si el array es corto, aunque el array necesita ser ordenados de antemano. Todos los algoritmos de clasificación basados en la comparación de elementos, como rápidos y de fusión, requieren al menos ${textstyle O(nlog n)}$ comparaciones en el peor de los casos. A diferencia de la búsqueda lineal, la búsqueda binaria se puede utilizar para una coincidencia aproximada eficiente. Hay operaciones tales como encontrar el elemento más pequeño y más grande que se puede hacer eficientemente en un array ordenados pero no en un array sin surtido.

Árboles

Los árboles de búsqueda binaria se buscan usando un algoritmo similar a la búsqueda binaria.

Un árbol de búsqueda binario es una estructura de datos de árbol binario que funciona según el principio de búsqueda binaria. Los registros del árbol se organizan en orden, y cada registro del árbol se puede buscar utilizando un algoritmo similar a la búsqueda binaria, tomando un tiempo logarítmico promedio. La inserción y la eliminación también requieren un tiempo logarítmico promedio en los árboles de búsqueda binarios. Esto puede ser más rápido que la inserción y eliminación de matrices ordenadas en el tiempo lineal, y los árboles binarios conservan la capacidad de realizar todas las operaciones posibles en una matriz ordenada, incluidas las consultas aproximadas y de rango.

Sin embargo, la búsqueda binaria es generalmente más eficiente para buscar como árboles de búsqueda binaria probablemente será imperfectamente equilibrada, lo que resulta en un rendimiento ligeramente peor que la búsqueda binaria. Esto incluso se aplica a los árboles de búsqueda binaria equilibrados, los árboles de búsqueda binaria que equilibran sus propios nodos, porque rara vez producen el árbol con los niveles más bajos posibles. Excepto por árboles de búsqueda binaria equilibrados, el árbol puede estar gravemente desequilibrado con pocos ganglios internos con dos niños, lo que resulta en el tiempo de búsqueda promedio y el peor de los casos que se aproxima. ${textstyle n}$ comparaciones. Los árboles de búsqueda binaria tienen más espacio que los arrays ordenados.

Los árboles de búsqueda binarios se prestan para realizar búsquedas rápidas en la memoria externa almacenada en discos duros, ya que los árboles de búsqueda binarios se pueden estructurar de manera eficiente en sistemas de archivos. El árbol B generaliza este método de organización del árbol. Los árboles B se utilizan con frecuencia para organizar el almacenamiento a largo plazo, como bases de datos y sistemas de archivos.

Hashing

Para implementar matrices asociativas, las tablas hash, una estructura de datos que asigna claves a registros mediante una función hash, son generalmente más rápidas que la búsqueda binaria en una matriz ordenada de registros. La mayoría de las implementaciones de tablas hash requieren solo un tiempo constante amortizado en promedio. Sin embargo, el hashing no es útil para coincidencias aproximadas, como calcular la siguiente clave más pequeña, la siguiente más grande y la más cercana, ya que la única información proporcionada en una búsqueda fallida es que el objetivo no está presente en ningún registro. La búsqueda binaria es ideal para tales coincidencias, realizándolas en tiempo logarítmico. La búsqueda binaria también admite coincidencias aproximadas. Algunas operaciones, como encontrar el elemento más pequeño y el más grande, se pueden realizar de manera eficiente en matrices ordenadas pero no en tablas hash.

Establecer algoritmos de membresía

Un problema relacionado con la búsqueda se establece la membresía. Cualquier algoritmo que hace búsqueda, como búsqueda binaria, también se puede utilizar para la membresía de conjunto. Hay otros algoritmos que son más específicamente adecuados para la membresía de conjunto. Una matriz de bits es la más simple, útil cuando la gama de teclas es limitada. Almacena compactamente una colección de bits, con cada bit representando una sola llave dentro de la gama de llaves. Los arrays de bits son muy rápidos, requiriendo sólo ${textstyle O(1)}$ tiempo. El tipo Judy1 de Judy array maneja las teclas de 64 bits de manera eficiente.

Para resultados aproximados, filtros Bloom, otra estructura probabilística de datos basada en la piratería, almacenar un conjunto de teclas mediante la codificación de las teclas utilizando una matriz de bits y múltiples funciones de hash. Los filtros de Bloom son mucho más eficientes que los arrays de bits en la mayoría de los casos y no mucho más lento: con ${textstyle k}$ funciones de hash, consultas de membresía ${textstyle O(k)}$ tiempo. Sin embargo, los filtros Bloom sufren de falsos positivos.

Otras estructuras de datos

Existen estructuras de datos que pueden mejorar la búsqueda binaria en algunos casos tanto para la búsqueda como para otras operaciones disponibles para matrices ordenadas. Por ejemplo, las búsquedas, las coincidencias aproximadas y las operaciones disponibles para las matrices ordenadas se pueden realizar de manera más eficiente que la búsqueda binaria en estructuras de datos especializadas, como árboles de van Emde Boas, árboles de fusión, intentos y matrices de bits. Estas estructuras de datos especializadas generalmente solo son más rápidas porque aprovechan las propiedades de las claves con un determinado atributo (generalmente claves que son números enteros pequeños) y, por lo tanto, consumirán tiempo o espacio para las claves que carecen de ese atributo. Siempre que se puedan ordenar las claves, estas operaciones siempre se pueden realizar al menos de manera eficiente en una matriz ordenada, independientemente de las claves. Algunas estructuras, como los arreglos Judy, usan una combinación de enfoques para mitigar esto mientras conservan la eficiencia y la capacidad de realizar coincidencias aproximadas.

Variaciones

Búsqueda binaria uniforme

La búsqueda binaria uniforme almacena la diferencia entre la corriente y los dos próximos elementos medios posibles en lugar de límites específicos.

Tiendas de búsqueda binaria uniformes, en lugar de los límites inferiores y superiores, la diferencia en el índice del elemento medio de la iteración actual a la próxima iteración. Una tabla de búsqueda que contiene las diferencias se calcula de antemano. Por ejemplo, si el array a buscar es $[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]$ , el elemento medio ( $m$ ) sería $6$ . En este caso, el elemento medio del subarray izquierdo ( $[1, 2, 3, 4, 5]$ ) es $3$ y el elemento medio del subarray derecho ( $[7, 8, 9, 10, 11]$ ) es $9$ . Búsqueda binaria uniforme almacenaría el valor de $3$ como ambos índices difieren de $6$ por esta misma cantidad. Para reducir el espacio de búsqueda, el algoritmo añade o resta este cambio del índice del elemento medio. La búsqueda binaria uniforme puede ser más rápida en sistemas donde es ineficiente para calcular el punto medio, como en computadoras decimales.

Búsqueda exponencial

Visualización de búsqueda exponencial encontrando el límite superior para la búsqueda binaria posterior

La búsqueda exponencial extiende la búsqueda binaria a listas sin límites. Comienza encontrando el primer elemento con un índice que es tanto un poder de dos y mayor que el valor objetivo. Después, establece ese índice como el límite superior, y cambia a búsqueda binaria. Una búsqueda requiere ${textstyle lfloor log _{2}x+1rfloor }$ iteraciones antes de la búsqueda binaria se inicia y ${textstyle lfloor log _{2}xrfloor }$ iteraciones de la búsqueda binaria, donde ${textstyle x}$ es la posición del valor objetivo. La búsqueda exponencial funciona en listas limitadas, pero se convierte en una mejora sobre la búsqueda binaria sólo si el valor objetivo está cerca del comienzo de la matriz.

Búsqueda de interpolación

Visualización de búsqueda de interpolación mediante interpolación lineal. En este caso, no se necesita ninguna búsqueda porque la estimación de la ubicación del objetivo dentro del array es correcta. Otras implementaciones pueden especificar otra función para estimar la ubicación del objetivo.

En lugar de calcular el punto medio, la búsqueda por interpolación estima la posición del valor de destino, teniendo en cuenta los elementos más altos y más bajos de la matriz, así como la longitud de la matriz. Funciona sobre la base de que el punto medio no es la mejor suposición en muchos casos. Por ejemplo, si el valor de destino está cerca del elemento más alto de la matriz, es probable que se encuentre cerca del final de la matriz.

Una función común de interpolación es la interpolación lineal. Si $A$ es el array, ${displaystyle L,R}$ son los límites inferiores y superiores respectivamente, y $T$ es el objetivo, entonces se calcula que el objetivo es ${displaystyle (T-A_{L})/(A_{R}-A_{L})}$ del camino entre $L$ y $R$ . Cuando se utiliza la interpolación lineal, y la distribución de los elementos de matriz es uniforme o casi uniforme, la búsqueda de interpolación hace ${textstyle O(log log n)}$ comparaciones.

En la práctica, la búsqueda por interpolación es más lenta que la búsqueda binaria para arreglos pequeños, ya que la búsqueda por interpolación requiere un cálculo adicional. Su complejidad de tiempo crece más lentamente que la búsqueda binaria, pero esto solo compensa el cálculo adicional para matrices grandes.

Cascada fraccional

En cascada fraccional, cada matriz tiene punteros a cada segundo elemento de otro array, por lo que sólo una búsqueda binaria tiene que ser realizada para buscar todos los arrays.

La cascada fraccional es una técnica que acelera búsquedas binarias para el mismo elemento en múltiples arrays ordenados. Buscar cada matriz por separado requiere ${textstyle O(klog n)}$ tiempo, donde ${textstyle k}$ es el número de arrays. Cadena fraccional reduce esto a ${textstyle O(k+log n)}$ almacenando información específica en cada matriz sobre cada elemento y su posición en los otros arrays.

La cascada fraccional se desarrolló originalmente para resolver de manera eficiente varios problemas de geometría computacional. La cascada fraccional se ha aplicado en otros lugares, como en la minería de datos y el enrutamiento del Protocolo de Internet.

Generalización a gráficos

La búsqueda binaria se ha generalizado para trabajar en ciertos tipos de gráficos, donde el valor objetivo se almacena en un vértice en lugar de un elemento array. Los árboles de búsqueda binaria son una de tales generalización—cuando un vértice (nodo) en el árbol se pregunta, el algoritmo sabe que el vértice es el objetivo, o de lo contrario en qué subárbol se ubicaría el objetivo. Sin embargo, esto se puede generalizar más de la siguiente manera: dado un gráfico no dirigido y ponderado positivamente y un vértice objetivo, el algoritmo aprende sobre la búsqueda de un vértice que es igual al objetivo, o se le da un borde de incidente que está en el camino más corto desde el vértice queried al objetivo. El algoritmo de búsqueda binaria estándar es simplemente el caso donde el gráfico es un camino. Del mismo modo, los árboles de búsqueda binaria son el caso en que los bordes de los subárboles izquierdos o derecho se dan cuando el vértice dañado es desigual al objetivo. Para todos los gráficos no dirigidos, de peso positivo, hay un algoritmo que encuentra el vértice objetivo en $O(log n)$ consultas en el peor caso.

Búsqueda binaria ruidosa

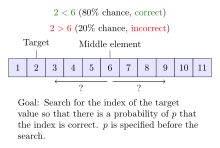
En la búsqueda binaria ruidosa, existe cierta probabilidad de que una comparación sea incorrecta.

Noisy algoritmos de búsqueda binaria solucionan el caso donde el algoritmo no puede comparar fiablemente elementos de la matriz. Para cada par de elementos, existe cierta probabilidad de que el algoritmo haga la comparación equivocada. La búsqueda binaria ruidosa puede encontrar la posición correcta del objetivo con una probabilidad dada que controla la fiabilidad de la posición cedida. Cada procedimiento de búsqueda binaria ruidosa debe hacer al menos ${displaystyle (1-tau){frac {log _{2}(n)}{H(p)}}-{frac {10}{H(p)}}}$ comparaciones en promedio, donde ${displaystyle H(p)=-plog _{2}(p)-(1-p)log _{2}(1-p)}$ es la función binaria entropía y $tau$ es la probabilidad de que el procedimiento rinda la posición equivocada. El ruidoso problema de búsqueda binaria se puede considerar como un caso del juego Rényi-Ulam, una variante de Veinte preguntas donde las respuestas pueden ser erróneas.

Búsqueda binaria cuántica

Las computadoras clásicas están sujetas al peor caso de exactamente ${textstyle lfloor log _{2}n+1rfloor }$ iteraciones al realizar búsqueda binaria. Los algoritmos cuánticos para la búsqueda binaria todavía están vinculados a una proporción de ${textstyle log _{2}n}$ consultas (que representan iteraciones del procedimiento clásico), pero el factor constante es inferior a uno, proporcionando una menor complejidad de tiempo en las computadoras cuánticas. Cualquier exacta procedimiento de búsqueda binaria cuántica, es decir, un procedimiento que siempre produce el resultado correcto, requiere al menos ${textstyle {frac {1}{pi }}(ln n-1)approx 0.22log _{2}n}$ consultas en el peor de los casos, donde ${textstyle ln }$ es el logaritmo natural. Hay un procedimiento exacto de búsqueda binaria cuántica que funciona en ${textstyle 4log _{605}napprox 0.433log _{2}n}$ consultas en el peor caso. En comparación, el algoritmo de Grover es el algoritmo cuántico óptimo para buscar una lista no ordenada de elementos, y requiere $O({sqrt {n}})$ consultas.

Historia

La idea de ordenar una lista de elementos para permitir una búsqueda más rápida se remonta a la antigüedad. El ejemplo más antiguo conocido fue la tablilla Inakibit-Anu de Babilonia que data de c. 200 BCE. La tableta contenía alrededor de 500 números sexagesimales y sus recíprocos clasificados en orden lexicográfico, lo que facilitó la búsqueda de una entrada específica. Además, se descubrieron en las islas del Egeo varias listas de nombres ordenados por su primera letra. Catholicon, un diccionario de latín terminado en 1286 d. C., fue el primer trabajo que describió las reglas para clasificar las palabras en orden alfabético, a diferencia de solo las primeras letras.

En 1946, John Mauchly hizo la primera mención de la búsqueda binaria como parte de las Conferencias de la Escuela Moore, un curso universitario fundamental y fundacional en computación. En 1957, William Wesley Peterson publicó el primer método de búsqueda por interpolación. Todos los algoritmos de búsqueda binaria publicados funcionaron solo para matrices cuya longitud es uno menos que una potencia de dos hasta 1960, cuando Derrick Henry Lehmer publicó un algoritmo de búsqueda binaria que funcionaba en todas las matrices. En 1962, Hermann Bottenbruch presentó una implementación de búsqueda binaria ALGOL 60 que colocaba la comparación por igualdad al final, aumentando el número promedio de iteraciones en uno, pero reduciendo a uno el número de comparaciones por iteración. La búsqueda binaria uniforme fue desarrollada por A. K. Chandra de la Universidad de Stanford en 1971. En 1986, Bernard Chazelle y Leonidas J. Guibas introdujeron la cascada fraccionaria como método para resolver numerosos problemas de búsqueda en geometría computacional.

Problemas de implementación

Aunque la idea básica de la búsqueda binaria es comparativamente sencilla, los detalles pueden ser sorprendentemente difíciles
—Donald Knuth

Cuando Jon Bentley asignó la búsqueda binaria como un problema en un curso para programadores profesionales, descubrió que el noventa por ciento no proporcionaba una solución correcta después de varias horas de trabajo en ella, principalmente porque las implementaciones incorrectas no se ejecutaban o devolvían un error. respuesta en casos extremos raros. Un estudio publicado en 1988 muestra que el código exacto solo se encuentra en cinco de veinte libros de texto. Además, la propia implementación de la búsqueda binaria de Bentley, publicada en su libro de 1986 Programming Pearls, contenía un error de desbordamiento que no se detectó durante más de veinte años. La implementación de la biblioteca del lenguaje de programación Java de la búsqueda binaria tuvo el mismo error de desbordamiento durante más de nueve años.

En una aplicación práctica, las variables utilizadas para representar los índices a menudo serán de tamaño fijo (integers), y esto puede dar lugar a un desbordamiento aritmético para arrays muy grandes. Si el punto medio del lazo se calcula como ${displaystyle {frac {L+R}{2}}}$ , entonces el valor de $L+R$ puede exceder el rango de enteros del tipo de datos utilizado para almacenar el punto medio, incluso si $L$ y $R$ están dentro del rango. Si $L$ y $R$ no negativo, esto se puede evitar calculando el punto medio como ${displaystyle L+{frac {R-L}{2}}}$ .

Un bucle infinito puede ocurrir si las condiciones de salida para el bucle no se definen correctamente. Una vez $L$ excedentes $R$ , la búsqueda ha fallado y debe transmitir el fracaso de la búsqueda. Además, el bucle debe salir cuando se encuentra el elemento objetivo, o en el caso de una implementación donde este cheque se traslada al final, comprobar si la búsqueda fue exitosa o fallida al final debe estar en su lugar. Bentley encontró que la mayoría de los programadores que implementaron incorrectamente la búsqueda binaria cometió un error en la definición de las condiciones de salida.

Apoyo bibliotecario

Muchos idiomas' Las bibliotecas estándar incluyen rutinas de búsqueda binaria:

C proporciona la función bsearch() en su biblioteca estándar, que normalmente se implementa mediante búsqueda binaria, aunque el estándar oficial no lo requiere.
La Biblioteca de Plantillas Estándar de C++ ofrece las funciones binary_search(), lower_bound(), upper_bound() y equal_range().
D's standard library Phobos, in std.range módulo proporciona un tipo SortedRange (retornado por sort() y assumeSorted() funciones) con métodos contains(), equaleRange(), lowerBound() y trisect(), que utilizan técnicas de búsqueda binaria por defecto para rangos que ofrecen acceso aleatorio.
COBOL proporciona el SEARCH ALL verbo para realizar búsquedas binarias en las tablas ordenadas COBOL.
Vamos. sort paquete de biblioteca estándar contiene las funciones Search, SearchInts, SearchFloat64s, y SearchStrings, que implementa búsqueda binaria general, así como implementaciones específicas para la búsqueda de rebanadas de enteros, números de puntos flotantes y cadenas, respectivamente.
Java ofrece un conjunto de sobrecarga binarySearch() métodos estáticos en las clases Arrays y Collections en el estándar java.util paquete para realizar búsquedas binarias en arrays Java y en Lists, respectivamente.
Microsoft's.NET Framework 2.0 ofrece versiones estáticas genéricas del algoritmo de búsqueda binaria en sus clases base de colección. Un ejemplo sería System.ArrayEl método BinarySearch(T[] array, T value).
Para Objetivo-C, el marco Cocoa proporciona el NSArray -indexOfObject:inSortedRange:options:usingComparator: método en Mac OS X 10.6+. Apple Core Foundation C framework also contains a CFArrayBSearchValues() función.
Python proporciona el bisect módulo que mantiene una lista en orden ordenado sin tener que ordenar la lista después de cada inserción.
La clase Array de Ruby incluye una bsearch método con ajuste aproximado incorporado.

Notas y referencias

Este artículo fue presentado WikiJournal of Science para el examen académico externo de pares en 2018 (revisores reportes). El contenido actualizado se reintegra en la página de Wikipedia bajo una licencia CC-BY-SA-3.02019). La versión del registro que se examina es: Anthony Lin; et al. (2 de julio de 2019). " algoritmo de búsqueda interna" (PDF). WikiJournal of Science. 2 (1): 5. doi:10.15347/WJS/2019.005. ISSN 2470-6345. Wikidata Q81434400.

Contenido relacionado

Más resultados...