Algoritmo de búsqueda A*

A* (pronunciado "A-star") es un algoritmo de graph traversal y búsqueda de caminos, que se utiliza en muchos campos de la ciencia informática debido a su integridad, optimización y eficiencia óptima. Un importante inconveniente práctico es su O()bd){displaystyle O(b^{d}} complejidad espacial, ya que almacena todos los nodos generados en la memoria. Por lo tanto, en sistemas prácticos de viaje, generalmente es superado por algoritmos que pueden pre-procesar el gráfico para obtener un mejor rendimiento, así como enfoques basados en la memoria; sin embargo, A* sigue siendo la mejor solución en muchos casos.

Peter Hart, Nils Nilsson y Bertram Raphael del Stanford Research Institute (ahora SRI International) publicaron el algoritmo por primera vez en 1968. Puede verse como una extensión del algoritmo de Dijkstra. A* logra un mejor desempeño al usar heurísticas para guiar su búsqueda.

En comparación con el algoritmo de Dijkstra, el algoritmo A* solo encuentra la ruta más corta desde una fuente específica hasta un objetivo específico, y no el árbol de la ruta más corta desde una fuente específica hasta todos los objetivos posibles. Esta es una compensación necesaria para usar una heurística dirigida a un objetivo específico. Para el algoritmo de Dijkstra, dado que se genera todo el árbol de la ruta más corta, cada nodo es un objetivo y no puede haber una heurística dirigida a un objetivo específico.

Historia

A* fue inventado por investigadores trabajando en la planificación de la trayectoria de Shakey the Robot.

A* se creó como parte del proyecto Shakey, cuyo objetivo era construir un robot móvil que pudiera planificar sus propias acciones. Nils Nilsson propuso originalmente usar el algoritmo Graph Traverser para la planificación de rutas de Shakey. Graph Traverser se guía por una función heurística h(n), la distancia estimada desde el nodo n al nodo objetivo: ignora por completo g(n), la distancia desde el nodo de inicio hasta n. Bertram Raphael sugirió usar la suma, g(n) + h(n). Peter Hart inventó los conceptos que ahora llamamos admisibilidad y consistencia de las funciones heurísticas. A* se diseñó originalmente para encontrar caminos de costo mínimo cuando el costo de un camino es la suma de sus costos, pero se ha demostrado que A* se puede usar para encontrar caminos óptimos para cualquier problema que satisfaga las condiciones de un álgebra de costos.

El documento A* original de 1968 contenía un teorema que afirmaba que ningún algoritmo similar a A* podría expandir menos nodos que A* si la función heurística es consistente y la regla de desempate de A* se elige adecuadamente. Unos años más tarde se publicó una ″corrección″ afirmando que no se requería consistencia, pero se demostró que esto era falso en el estudio definitivo de Dechter y Pearl sobre la optimización de A* (ahora llamada eficiencia óptima), que dio un ejemplo de A* con una heurística que era admisible pero no consistente expandiendo arbitrariamente más nodos que un algoritmo alternativo similar a A*.

Descripción

Un algoritmo de búsqueda de ruta que navega alrededor de un laberinto generado aleatoriamente

A* es un algoritmo de búsqueda informada, o una búsqueda de lo mejor primero, lo que significa que está formulado en términos de gráficos ponderados: a partir de un nodo de inicio específico de un gráfico, su objetivo es encontrar una ruta hacia el nodo de destino dado. tener el menor costo (menor distancia recorrida, menor tiempo, etc.). Lo hace manteniendo un árbol de caminos que se originan en el nodo de inicio y extendiendo esos caminos un borde a la vez hasta que se satisface su criterio de terminación.

En cada iteración de su ciclo principal, A* necesita determinar cuál de sus rutas extender. Lo hace en función del costo del camino y una estimación del costo requerido para extender el camino hasta la meta. Específicamente, A* selecciona el camino que minimiza

f()n)=g()n)+h()n){displaystyle f(n)=g(n)+h(n)}

donde n es el siguiente nodo en la ruta, g(n) es el costo de la ruta desde el nodo de inicio hasta n, y h(n) es una función heurística que estima el costo de la ruta más económica desde n al objetivo. A* termina cuando la ruta que elige extender es una ruta de inicio a meta o si no hay rutas elegibles para extenderse. La función heurística es específica del problema. Si la función heurística es admisible, lo que significa que nunca sobrestima el costo real para llegar a la meta, se garantiza que A* devolverá una ruta de menor costo desde el principio hasta la meta.

Las implementaciones típicas de A* usan una cola de prioridad para realizar la selección repetida de nodos de costo mínimo (estimado) para expandir. Esta cola de prioridad se conoce como conjunto abierto, margen o frontera. En cada paso del algoritmo, el nodo con el valor f(x) más bajo se elimina de la cola, el Valores f y g de sus vecinos se actualizan en consecuencia y estos vecinos se agregan a la cola. El algoritmo continúa hasta que un nodo eliminado (por lo tanto, el nodo con el valor f más bajo de todos los nodos marginales) es un nodo objetivo. El valor f de ese objetivo es también el costo del camino más corto, ya que h en el objetivo es cero en una heurística admisible.

El algoritmo descrito hasta ahora nos da solo la longitud del camino más corto. Para encontrar la secuencia real de pasos, el algoritmo se puede revisar fácilmente para que cada nodo en la ruta siga la pista de su predecesor. Después de ejecutar este algoritmo, el nodo final apuntará a su predecesor, y así sucesivamente, hasta que el predecesor de algún nodo sea el nodo inicial.

Como ejemplo, al buscar la ruta más corta en un mapa, h(x) podría representar la distancia en línea recta a la meta, ya que es físicamente la distancia más pequeña posible entre dos puntos cualesquiera. Para un mapa de cuadrícula de un videojuego, el uso de la distancia de Manhattan o la distancia de octile se vuelve mejor según el conjunto de movimientos disponibles (4 vías u 8 vías).

Si la heurística h satisface la condición adicional h (x) ≤ d(x, y) + h(y) para cada borde (x, y) del gráfico (donde d indica la longitud de ese borde), luego h se llama monótono o consistente. Con una heurística consistente, se garantiza que A* encontrará una ruta óptima sin procesar ningún nodo más de una vez y A* es equivalente a ejecutar el algoritmo de Dijkstra con el costo reducido d& #39;(x, y) = d(x, y) + h(y) − h(x).

Pseudocódigo

El siguiente pseudocódigo describe el algoritmo:

función reconstruct_path()Vino, corriente) total_path := {current} mientras corriente dentro Vino.Llaves: corriente := Vino[corriente] total_path.prepensión()corriente) retorno total_path// A* encuentra un camino de principio a fin.// h es la función heurística. h(n) estima el costo para alcanzar la meta desde el nodo n.función A_Star()Empieza, meta, h) // El conjunto de nodos descubiertos que pueden necesitar ser (re-)expandidos. // Inicialmente, sólo se conoce el nodo inicial. // Esto generalmente se implementa como una cola de minutos o prioridad en lugar de un hash-set. abierto Set := {start} // Para el nodo n, vinoDe[n] es el nodo inmediatamente anterior a él en la ruta más barata desde el principio // a n actualmente conocido. Vino := an vacío mapa // Para nodo n, gScore[n] es el costo de la ruta más barata de principio a n actualmente conocido. gScore := mapa con por defecto valor de Infinity gScore[Empieza] := 0 // Para el nodo n, fScore[n]:= gScore[n] + h(n). fScore[n] representa nuestra mejor suposición actual // cuan barato un camino podría ser de principio a fin si pasa por n. fScore := mapa con por defecto valor de Infinity fScore[Empieza] := h()Empieza) mientras abierto Set es no vacío // Esta operación puede ocurrir en tiempo O(Log(N) si está abierta El juego es un min-heap o una cola de prioridad corriente := el nodos dentro abierto Set teniendo el más bajo fScore[] valor si corriente = meta retorno reconstruct_path()Vino, corriente) abierto Set.Retirar()corriente) para cada uno vecino de corriente // d(actual, vecino) es el peso del borde de corriente a vecino // tentativo_g Puntuación es la distancia desde el principio al vecino a través de la corriente tentativo_gScore := gScore[corriente] + d()corriente, vecino) si tentativo_gScore . gScore[vecino] // Este camino al prójimo es mejor que cualquier anterior. ¡Regístrelo! Vino[vecino] := corriente gScore[vecino] := tentativo_gScore fScore[vecino] := tentativo_gScore + h()vecino) si vecino no dentro abierto Set abierto Set.añadir()vecino) // El juego abierto está vacío pero el objetivo nunca fue alcanzado retorno fracaso

Observación: En este pseudocódigo, si se llega a un nodo por una ruta, se elimina de openSet y luego se llega a través de una ruta más barata, se agregará a openSet nuevamente. Esto es fundamental para garantizar que el camino devuelto sea óptimo si la función heurística es admisible pero no consistente. Si la heurística es consistente, cuando se elimina un nodo de openSet, se garantiza que la ruta hacia él sea óptima, por lo que la prueba 'tentative_gScore < gScore[neighbor]’ siempre fallará si se vuelve a alcanzar el nodo.

Ilustración de A* busca encontrar el camino de un nodo de inicio a un nodo de meta en un problema de planificación de movimiento robot. Los círculos vacíos representan los nodos en los abierto, es decir, los que quedan por explorar, y los llenos están en el conjunto cerrado. El color en cada nodo cerrado indica la distancia de la meta: el más verde, el más cercano. Uno puede ver primero la A* en una línea recta en la dirección del objetivo, luego al golpear el obstáculo, explora rutas alternativas a través de los nodos desde el conjunto abierto.

Ejemplo

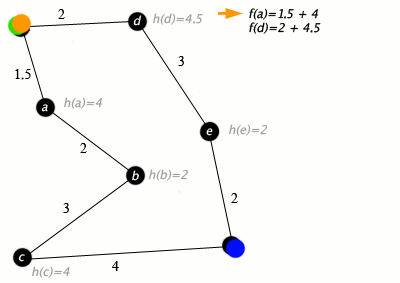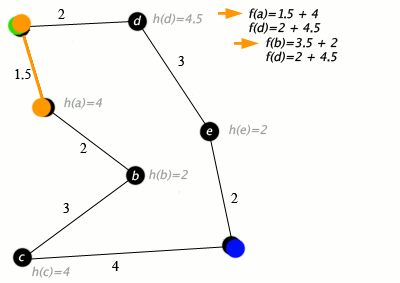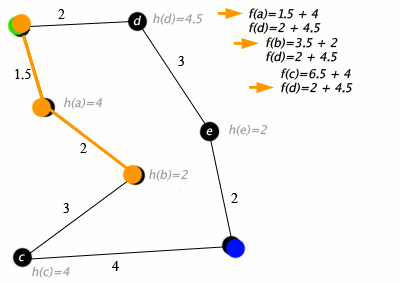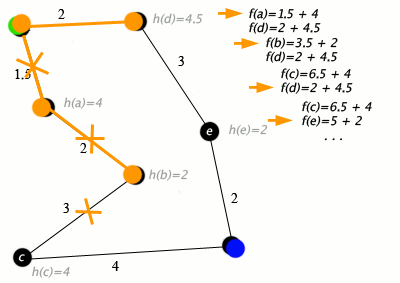
Un ejemplo de un algoritmo A* en acción donde los nodos son ciudades conectadas con carreteras y h(x) es la distancia en línea recta al punto objetivo:

Tecla: verde: inicio; azul: meta; naranja: visitado

El algoritmo A* también tiene aplicaciones en el mundo real. En este ejemplo, los bordes son vías férreas y h(x) es la distancia de gran círculo (la distancia más corta posible en una esfera) al objetivo. El algoritmo está buscando un camino entre Washington, D.C. y Los Ángeles.

Detalles de implementación

Hay una serie de optimizaciones simples o detalles de implementación que pueden afectar significativamente el rendimiento de una implementación A*. El primer detalle a tener en cuenta es que la forma en que la cola de prioridad maneja los empates puede tener un efecto significativo en el rendimiento en algunas situaciones. Si se rompen los empates para que la cola se comporte de manera LIFO, A* se comportará como una búsqueda en profundidad entre rutas de igual costo (evitando explorar más de una solución igualmente óptima).

Cuando se requiere una ruta al final de la búsqueda, es común mantener con cada nodo una referencia al padre de ese nodo. Al final de la búsqueda, estas referencias se pueden utilizar para recuperar la ruta óptima. Si se mantienen estas referencias, puede ser importante que el mismo nodo no aparezca en la cola de prioridad más de una vez (cada entrada corresponde a una ruta diferente al nodo y cada una con un costo diferente). Un enfoque estándar aquí es verificar si un nodo a punto de agregarse ya aparece en la cola de prioridad. Si es así, los punteros de prioridad y padre se cambian para corresponder a la ruta de menor costo. Una cola de prioridad estándar basada en almacenamiento dinámico binario no admite directamente la operación de búsqueda de uno de sus elementos, pero se puede aumentar con una tabla hash que asigna elementos a su posición en el almacenamiento dinámico, lo que permite que esta operación de prioridad decreciente se realice en tiempo logarítmico. Alternativamente, un montón de Fibonacci puede realizar las mismas operaciones de prioridad decreciente en un tiempo amortizado constante.

Casos especiales

El algoritmo de Dijkstra, como otro ejemplo de un algoritmo de búsqueda de costos uniformes, se puede ver como un caso especial de A* donde h()x)=0{displaystyle h(x)=0} para todos x. La búsqueda general de profundidad se puede realizar utilizando A* considerando que hay un contador global C inicializado con un valor muy grande. Cada vez que procesamos un nodo que asignamos C a todos sus vecinos recién descubiertos. Después de cada asignación, disminuimos el contador C por uno. Así el anterior se descubre un nodo, el mayor es h()x){displaystyle h(x)} valor. Tanto el algoritmo de Dijkstra como la búsqueda de profundidad pueden implementarse más eficientemente sin incluir un h()x){displaystyle h(x)} valor en cada nodo.

Propiedades

Terminación e integridad

En gráficos finitos con pesos de borde no negativo A* está garantizada a rescindir y completo, es decir, siempre encontrará una solución (un camino de principio a fin) si existe. En gráficos infinitos con un factor de ramificación finito y los costos de borde que se atan lejos de cero (varepsilon >0}" xmlns="http://www.w3.org/1998/Math/MathML">d()x,Sí.)■ε ε ■0{textstyle d(x,y)varepsilon >0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/cbd9cce14624b15efd9312c81005c789de46285f" style="vertical-align: -0.838ex; width:14.987ex; height:2.843ex;"/> para algunos fijos ε ε {displaystyle varepsilon }), A* está garantizada a terminar sólo si existe una solución.

Admisibilidad

Se dice que un algoritmo de búsqueda es admisible si se garantiza que devolverá una solución óptima. Si la función heurística utilizada por A* es admisible, entonces A* es admisible. Una ″prueba″ intuitiva de esto es la siguiente:

Cuando A* termina su búsqueda, ha encontrado un camino de principio a fin cuyo costo real es menor que el costo estimado de cualquier camino de principio a meta a través de cualquier nodo abierto (el nodo f{displaystyle f} valor). Cuando la heurística es admisible, esas estimaciones son optimistas (no muy—ver el siguiente párrafo), por lo que A* puede ignorar con seguridad esos nodos porque no pueden conducir a una solución más barata que la que ya tiene. En otras palabras, A* nunca pasará por alto la posibilidad de un camino de bajo costo desde el principio hasta el objetivo, por lo que seguirá buscando hasta que no existan tales posibilidades.

La prueba real está un poco más involucrada porque la f{displaystyle f} los valores de los nodos abiertos no están garantizados para ser optimistas incluso si la heurística es admisible. Esto es porque el g{displaystyle g} los valores de los nodos abiertos no están garantizados para ser óptimos, por lo que la suma g+h{displaystyle g+h} no está garantizado ser optimista.

Optimidad y consistencia

El algoritmo A es óptimamente eficiente con respecto a un conjunto de algoritmos alternativos Alts en un conjunto de problemas P si para cada problema P en P y todo algoritmo A′ en Alts, el conjunto de nodos expandidos por A al resolver P es un subconjunto (posiblemente igual) del conjunto de nodos expandidos por A′ al resolver P. El estudio definitivo de la eficiencia óptima de A* se debe a Rina Dechter y Judea Pearl. Consideraron una variedad de definiciones de Alts y P en combinación con la heurística de A* como meramente admisible o consistente y admisible a la vez. El resultado positivo más interesante que demostraron es que A*, con una heurística consistente, es óptimamente eficiente con respecto a todos los algoritmos de búsqueda similares a A* admisibles en todos los problemas de búsqueda ″no patológicos″. En términos generales, su noción del problema no patológico es lo que ahora entendemos por ″hasta el desempate″. Este resultado no se cumple si la heurística de A* es admisible pero no consistente. En ese caso, Dechter y Pearl demostraron que existen algoritmos similares a A* admisibles que pueden expandir arbitrariamente menos nodos que A* en algunos problemas no patológicos.

La eficiencia óptima se trata del conjunto de nodos expandidos, no del número de expansiones de nodos (el número de iteraciones del bucle principal de A*). Cuando la heurística utilizada es admisible pero no consistente, es posible que un nodo se expanda en A* muchas veces, un número exponencial de veces en el peor de los casos. En tales circunstancias, el algoritmo de Dijkstra podría superar a A* por un amplio margen. Sin embargo, investigaciones más recientes encontraron que este caso patológico solo ocurre en ciertas situaciones artificiales donde el peso del borde del gráfico de búsqueda es exponencial en el tamaño del gráfico y que ciertas heurísticas inconsistentes (pero admisibles) pueden conducir a un número reducido de expansiones de nodos. en búsquedas A*.

Relajación limitada

Una búsqueda* que utiliza una heurística que es 5.0(=ε) veces una heurística consistente, y obtiene un camino suboptimal.

Si bien el criterio de admisibilidad garantiza una ruta de solución óptima, también significa que A* debe examinar todas las rutas igualmente meritorias para encontrar la ruta óptima. Para calcular los caminos más cortos aproximados, es posible acelerar la búsqueda a expensas de la optimización relajando el criterio de admisibilidad. A menudo, queremos acotar esta relajación, de modo que podamos garantizar que la ruta de la solución no sea peor que (1 + ε) veces la ruta de la solución óptima. Esta nueva garantía se denomina ε-admisible.

Hay una serie de algoritmos admisibles para ε:

• Pesado A* / Peso Estatico. Si h_a()n) es una función heurística admisible, en la versión ponderada de la búsqueda A* se utiliza h_w()n) ε h_a()n), ε ■ 1 como la función heurística, y realizar la búsqueda A* como de costumbre (que eventualmente sucede más rápido que usar) h_a ya que se expanden menos nodos). El camino encontrado por el algoritmo de búsqueda puede tener un costo de la mayoría ε tiempos que de la ruta menos costosa en el gráfico.
• Peso dinámico utiliza la función de coste f()n)=g()n)+()1+ε ε w()n))h()n){displaystyle f(n)=g(n)+(1+varepsilon w(n)h(n)}, donde w()n)={}1− − d()n)Nd()n)≤ ≤ N0de otra manera{displaystyle w(n)={begin{cases}1-{frac {d(n)}{N} {d(n)leq N consiguiendo {text{otherwise}end{cases}}}}}, y dónde d()n){displaystyle d(n)} es la profundidad de la búsqueda y N es la longitud anticipada del camino de solución.
• Dinámica de muestreo Weighting utiliza el muestreo de nodos para estimar mejor y debias el error heurístico.
• Aε ε Alternativa Alternativa {displaystyle A_{varepsilon } {}}} {}}. usa dos funciones heurísticas. La primera es la lista FOCAL, que se utiliza para seleccionar los nodos candidatos, y la segunda h_F se utiliza para seleccionar el nodo más prometedor de la lista FOCAL.
• A_ε selecciona nodos con la función Af()n)+BhF()n){displaystyle Af(n)+Bh_{F}(n)}, donde A y B son constantes. Si no se pueden seleccionar nodos, el algoritmo retrocederá con la función Cf()n)+DhF()n){displaystyle Cf(n)+Dh_{F}(n)}, donde C y D son constantes.
• AlphA* intenta promover la explotación de la primera profundidad prefiriendo nodos recientemente ampliados. AlphA* utiliza la función de coste fα α ()n)=()1+wα α ()n))f()n){displaystyle f_{alpha }(n)=(1+w_{alpha }(n)f(n)}, donde wα α ()n)={}λ λ g()π π ()n))≤ ≤ g()n~ ~ )▪ ▪ de otra manera{displaystyle w_{alpha }(n)={begin{cases}lambda &g(pi (n))leq g({tilde {n})\Lambda >{otherwise}end{cases}}}}}}}}}}}, donde λ y ▪ son constantes con λ λ ≤ ≤ ▪ ▪ {displaystyle lambda leq Lambda }, π()n) es el padre de n, y ñ es el nodo más recientemente ampliado.

Complejidad

La complejidad temporal de A* depende de la heurística. En el peor de los casos de un espacio de búsqueda ilimitado, el número de nodos expandidos es exponencial en la profundidad de la solución (el camino más corto) d: O(b^d), donde b es el factor de ramificación (el número promedio de sucesores por estado). Esto supone que existe un estado objetivo y que se puede alcanzar desde el estado inicial; si no lo es, y el espacio de estados es infinito, el algoritmo no terminará.

La función heurística tiene un efecto importante en el rendimiento práctico de la búsqueda A*, ya que una buena heurística permite que A* elimine muchas de las b^d nodos que una búsqueda sin información ampliaría. Su calidad se puede expresar en términos del factor de ramificación efectivo b*, que se puede determinar empíricamente para una instancia de problema midiendo la cantidad de nodos generados por la expansión, N, y la profundidad de la solución, luego resolviendo

N+1=1+bAlternativa Alternativa +()bAlternativa Alternativa )2+⋯ ⋯ +()bAlternativa Alternativa )d.{displaystyle N+1=1+b^{*}+(b^{*})^{2}+dots +(b^{*}{d}.}

Las buenas heurísticas son aquellas con un factor de ramificación efectivo bajo (siendo el óptimo b* = 1).

La complejidad temporal es polinomial cuando el espacio de búsqueda es un árbol, existe un solo estado objetivo y la función heurística h cumple la siguiente condición:

Silencioh()x)− − hAlternativa Alternativa ()x)Silencio=O()log⁡ ⁡ hAlternativa Alternativa ()x)){displaystyle Silencioh(x)-h^{*}(x) habit=O(log h^{*}(x)}

donde h^* es la heurística óptima, el costo exacto para obtener de x a la meta. En otras palabras, el error de h no crecerá más rápido que el logaritmo de la "heurística perfecta" h^* que devuelve la distancia real desde x a la meta.

La complejidad espacial de A* es aproximadamente la misma que la de todos los demás algoritmos de búsqueda de gráficos, ya que mantiene todos los nodos generados en la memoria. En la práctica, este resulta ser el mayor inconveniente de la búsqueda A*, lo que lleva al desarrollo de búsquedas heurísticas limitadas por la memoria, como la profundización iterativa A*, la A* limitada por la memoria y la SMA*.

Aplicaciones

A* se usa a menudo para el problema común de búsqueda de rutas en aplicaciones como los videojuegos, pero originalmente se diseñó como un algoritmo general de recorrido de gráficos. Encuentra aplicaciones en diversos problemas, incluido el problema del análisis sintáctico utilizando gramáticas estocásticas en PNL. Otros casos incluyen una búsqueda de información con aprendizaje en línea.

Relaciones con otros algoritmos

Lo que distingue a A* de un codicioso algoritmo de búsqueda de lo mejor primero es que toma el costo/la distancia ya recorrida, g(n), en cuenta.

Algunas variantes comunes del algoritmo de Dijkstra se pueden ver como un caso especial de A* donde la heurística h()n)=0{displaystyle h(n)=0} para todos los nodos; a su vez, tanto Dijkstra como A* son casos especiales de programación dinámica. A* es en sí mismo un caso especial de generalización de ramas y límites.

Variantes

• En cualquier momento A*
• Bloqueo A*
• D*
• Campo D*
• Fringe
• Fringe Saving A* (FSA*)
• Adaptador generalizado A* (GAA*)
• Búsqueda heurística adicional
• Reducción A*
• Profundización iterativa A* (IDA*)
• Búsqueda de puntos de salto
• Planificación permanente A* (LPA*)
• New Bidirectional A* (NBA*)
• Memoria simplificada atada A* (SMA*)
• Theta*

A* también se puede adaptar a un algoritmo de búsqueda bidireccional. Se debe tener especial cuidado con el criterio de parada.