Algoritmo codicioso

Los algoritmos de salud determinan el número mínimo de monedas para dar mientras hace el cambio. Estos son los pasos que la mayoría de la gente tomaría para emular un algoritmo codicioso para representar 36 centavos utilizando sólo monedas con valores {1, 5, 10, 20}. La moneda del valor más alto, menos que el cambio restante adeudado, es el óptimo local. (En general, el problema de cambio requiere una programación dinámica para encontrar una solución óptima; sin embargo, la mayoría de los sistemas monetarios son casos especiales donde la estrategia avaricia encuentra una solución óptima.)

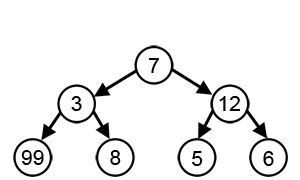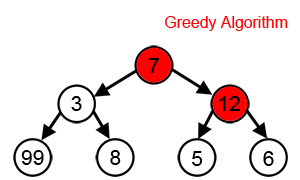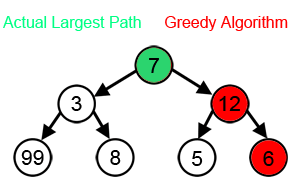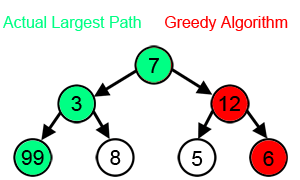
Un algoritmo codicioso es cualquier algoritmo que sigue la heurística de resolución de problemas de hacer la elección localmente óptima en cada etapa. En muchos problemas, una estrategia codiciosa no produce una solución óptima, pero una heurística codiciosa puede generar soluciones óptimas locales que se aproximan a una solución óptima global en un tiempo razonable.

Por ejemplo, una estrategia codiciosa para el problema del viajante de comercio (que es de alta complejidad computacional) es la siguiente heurística: "En cada paso del viaje, visite la ciudad no visitada más cercana." Esta heurística no pretende encontrar la mejor solución, pero termina en un número razonable de pasos; encontrar una solución óptima a un problema tan complejo generalmente requiere muchos pasos irrazonables. En la optimización matemática, los algoritmos voraces resuelven de manera óptima los problemas combinatorios que tienen las propiedades de los matroides y brindan aproximaciones de factor constante a los problemas de optimización con la estructura submodular.

Específicos

Los algoritmos codiciosos producen buenas soluciones en algunos problemas matemáticos, pero no en otros. La mayoría de los problemas para los que funcionan tendrán dos propiedades:

Propiedad buena elección

Podemos hacer cualquier elección parece mejor en este momento y luego resolver los subproblemas que surgen más adelante. La elección hecha por un algoritmo codicioso puede depender de las opciones tomadas hasta ahora, pero no de las futuras opciones o de todas las soluciones al subproblema. Iteratively hace una elección codictiva después de otra, reduciendo cada problema dado en uno más pequeño. En otras palabras, un algoritmo codicioso nunca reconsidera sus opciones. Esta es la principal diferencia de la programación dinámica, que es exhaustiva y está garantizada a encontrar la solución. Después de cada etapa, la programación dinámica toma decisiones basadas en todas las decisiones tomadas en la etapa anterior y puede reconsiderar el camino algoritmo de la etapa anterior a la solución.

Subestructura óptima

"Un problema muestra una subestructura óptima si una solución óptima al problema contiene soluciones óptimas a los subproblemas".

Casos de falla

Ejemplos sobre cómo un algoritmo codicioso puede no lograr la solución óptima.

Empezando desde A, un algoritmo codicioso que trata de encontrar el máximo siguiendo la mayor pendiente encontrará el máximo local en "m", oblividioso al máximo global en "M".

Para llegar a la suma más grande, en cada paso, el algoritmo codicioso elegirá lo que parece ser la elección inmediata óptima, por lo que elegirá 12 en lugar de 3 en el segundo paso, y no alcanzará la mejor solución, que contiene 99.

Los algoritmos codiciosos no logran producir la solución óptima para muchos otros problemas e incluso pueden producir la peor solución posible única. Un ejemplo es el problema del viajante de comercio mencionado anteriormente: para cada número de ciudades, hay una asignación de distancias entre las ciudades para las cuales la heurística del vecino más cercano produce el único peor recorrido posible. Para otros ejemplos posibles, consulte el efecto horizonte.

Tipos

Los algoritmos codiciosos se pueden caracterizar como "miope" y también como "no recuperables". Son ideales solo para problemas que tienen una 'subestructura óptima'. A pesar de esto, para muchos problemas simples, los algoritmos más adecuados son los codiciosos. Sin embargo, es importante tener en cuenta que el algoritmo voraz se puede usar como un algoritmo de selección para priorizar opciones dentro de una búsqueda o un algoritmo de ramificación y enlace. Hay algunas variaciones del algoritmo codicioso:

• algoritmos puramente codiciosos
• algoritmos codiciosos ortogonales
• algoritmos codiciosos relajados

Teoría

Los algoritmos codiciosos tienen una larga historia de estudio en optimización combinatoria e informática teórica. Se sabe que las heurísticas codiciosas producen resultados subóptimos en muchos problemas, por lo que las preguntas naturales son:

• ¿Para qué problemas funcionan los algoritmos codiciosos de manera óptima?
• ¿Para qué problemas los algoritmos codiciosos garantizan una solución óptima?
• Para qué problemas se garantiza el algoritmo codicioso no para producir una solución óptima?

Existe una gran cantidad de literatura que responde a estas preguntas para clases generales de problemas, como matroides, así como también para problemas específicos, como la cobertura fija.

Matroides

Una matroide es una estructura matemática que generaliza la noción de independencia lineal de espacios vectoriales a conjuntos arbitrarios. Si un problema de optimización tiene la estructura de un matroide, entonces el algoritmo voraz apropiado lo resolverá de manera óptima.

Funciones submodulares

Una función ${displaystyle f}$ definido en subconjuntos de un conjunto ${displaystyle Omega }$ se llama submodular si para cada ${displaystyle S,Tsubseteq Omega }$ tenemos ${displaystyle f(S)+f(T)geq f(Scup T)+f(Scap T)}$.

Supongamos que uno quiere encontrar un conjunto ${displaystyle S.$ que maximiza ${displaystyle f}$. El algoritmo codicioso, que construye un conjunto ${displaystyle S.$ agregando gradualmente el elemento que aumenta ${displaystyle f}$ el más a cada paso, produce como salida un conjunto que es al menos ${displaystyle (1-1/e)max _{Xsubseteq Omega }f(X)}$. Es decir, avaricia actúa dentro de un factor constante de ${displaystyle (1-1/e)approx 0.63}$ tan buena como la solución óptima.

Se pueden probar garantías similares cuando se imponen restricciones adicionales, como restricciones de cardinalidad, en la salida, aunque a menudo se requieren ligeras variaciones en el algoritmo voraz. Consulte para obtener una descripción general.

Otros problemas con las garantías

Otros problemas para los que el algoritmo voraz ofrece una fuerte garantía, pero no una solución óptima, incluyen

• Cubierta de conjunto
• El problema del árbol Steiner
• Equilibrio de carga
• Conjunto independiente

Muchos de estos problemas tienen límites inferiores coincidentes; es decir, el algoritmo codicioso no funciona mejor que la garantía en el peor de los casos.

Aplicaciones

Los algoritmos codiciosos por lo general (pero no siempre) no logran encontrar la solución óptima global porque, por lo general, no operan de manera exhaustiva en todos los datos. Pueden comprometerse con ciertas opciones demasiado pronto, lo que les impide encontrar la mejor solución general más adelante. Por ejemplo, todos los algoritmos de coloración codiciosos conocidos para el problema de coloración de gráficos y todos los demás problemas NP-completos no encuentran soluciones óptimas de manera consistente. Sin embargo, son útiles porque son rápidos de pensar y, a menudo, dan buenas aproximaciones al óptimo.

Si se puede demostrar que un algoritmo codicioso produce el óptimo global para una clase de problema dada, normalmente se convierte en el método de elección porque es más rápido que otros métodos de optimización como la programación dinámica. Ejemplos de tales algoritmos codiciosos son el algoritmo de Kruskal y el algoritmo de Prim para encontrar árboles de expansión mínimos y el algoritmo para encontrar árboles de Huffman óptimos.

Los algoritmos codiciosos también aparecen en el enrutamiento de la red. Mediante el enrutamiento codicioso, se reenvía un mensaje al nodo vecino que está "más cerca" al destino La noción de ubicación de un nodo (y, por lo tanto, de 'cercanía') puede determinarse por su ubicación física, como en el enrutamiento geográfico utilizado por las redes ad hoc. La ubicación también puede ser una construcción completamente artificial como en el enrutamiento de mundo pequeño y la tabla hash distribuida.

Ejemplos

• El problema de selección de actividades es característico de esta clase de problemas, donde el objetivo es elegir el número máximo de actividades que no chocan entre sí.
• En el ordenador Macintosh juego Búsqueda de cristal el objetivo es recoger cristales, de una manera similar al problema del vendedor viajero. El juego tiene un modo de demostración, donde el juego utiliza un algoritmo codicioso para ir a cada cristal. La inteligencia artificial no explica los obstáculos, por lo que el modo de demostración a menudo termina rápidamente.
• La búsqueda coincidente es un ejemplo de un algoritmo codicioso aplicado en la aproximación de señal.
• Un algoritmo codicioso encuentra la solución óptima al problema de Malfatti de encontrar tres círculos disjoint dentro de un triángulo dado que maximice el área total de los círculos; se conjetura que el mismo algoritmo codicioso es óptimo para cualquier número de círculos.
• Un algoritmo codicioso se utiliza para construir un árbol Huffman durante la codificación Huffman donde encuentra una solución óptima.
• En el aprendizaje de árboles de decisión, los algoritmos codiciosos se utilizan comúnmente, sin embargo no están garantizados para encontrar la solución óptima.
  • Un algoritmo tan popular es el algoritmo ID3 para la construcción de árboles de decisión.
• El algoritmo de Dijkstra y el algoritmo de búsqueda A* relacionado son algoritmos codiciosos verificablemente óptimos para la búsqueda de gráficos y encontrar el camino más corto.
  • Una búsqueda* es condicionalmente óptima, requiriendo una "heurística admisible" que no sobreestimará los costos de la ruta.
• El algoritmo de Kruskal y el algoritmo de Prim son algoritmos codiciosos para construir árboles mínimos de azotes de un gráfico conectado dado. Siempre encuentran una solución óptima, que puede no ser única en general.