Álgebra relacional

En la teoría de bases de datos, el álgebra relacional es una teoría que utiliza estructuras algebraicas para modelar datos y definir consultas sobre ellos con una semántica bien fundamentada. La teoría fue presentada por Edgar F. Codd.

La principal aplicación del álgebra relacional es proporcionar una base teórica para las bases de datos relacionales, en particular los lenguajes de consulta para dichas bases de datos, entre los que destaca SQL. Las bases de datos relacionales almacenan datos tabulares representados como relaciones. Las consultas sobre bases de datos relacionales a menudo también devuelven datos tabulares representados como relaciones.

El objetivo principal del álgebra relacional es definir operadores que transformen una o más relaciones de entrada en una relación de salida. Dado que estos operadores aceptan relaciones como entrada y producen relaciones como salida, pueden combinarse y usarse para expresar consultas potencialmente complejas que transforman potencialmente muchas relaciones de entrada (cuyos datos se almacenan en la base de datos) en una sola relación de salida (los resultados de la consulta).

Los operadores unarios aceptan como entrada una sola relación; los ejemplos incluyen operadores para filtrar ciertos atributos (columnas) o tuplas (filas) de una relación de entrada.

Los operadores binarios aceptan como entrada dos relaciones; dichos operadores combinan las dos relaciones de entrada en una sola relación de salida, por ejemplo, tomando todas las tuplas encontradas en cualquier relación, eliminando las tuplas de la primera relación encontradas en la segunda relación, extendiendo las tuplas de la primera relación con las tuplas de la segunda relación coincidiendo con ciertas condiciones, y así sucesivamente.

También se pueden incluir otros operadores más avanzados, donde la inclusión o exclusión de determinados operadores da lugar a una familia de álgebras.

Introducción

El álgebra relacional recibió poca atención fuera de las matemáticas puras hasta la publicación del modelo relacional de datos de E. F. Codd en 1970. Codd propuso este álgebra como base para los lenguajes de consulta de bases de datos. (Consulte la sección Implementaciones).

Cinco operadores primitivos del álgebra de Codd son la selección, la proyección, el producto cartesiano (también llamado producto cruzado o unión cruzada), la unión de conjuntos y la diferencia de conjuntos.

Operadores de conjuntos

El álgebra relacional utiliza la unión de conjuntos, la diferencia de conjuntos y el producto cartesiano de la teoría de conjuntos, pero agrega restricciones adicionales a estos operadores.

Para la unión de conjuntos y la diferencia de conjuntos, las dos relaciones involucradas deben ser compatibles con la unión, es decir, las dos relaciones deben tener el mismo conjunto de atributos. Debido a que la intersección de conjuntos se define en términos de unión de conjuntos y diferencia de conjuntos, las dos relaciones involucradas en la intersección de conjuntos también deben ser compatibles con la unión.

Para que se defina el producto cartesiano, las dos relaciones involucradas deben tener encabezados separados, es decir, no deben tener un nombre de atributo común.

Además, el producto cartesiano se define de manera diferente al de la teoría de conjuntos en el sentido de que las tuplas se consideran "superficiales" para los efectos de la operación. Es decir, el producto cartesiano de un conjunto de tuplas n con un conjunto de tuplas m produce un conjunto de tuplas "aplanadas" (n + m)-tuplas (mientras que la teoría básica de conjuntos habría prescrito un conjunto de 2 tuplas, cada una conteniendo una tupla n y una tupla m). Más formalmente, R × S se define de la siguiente manera:

La cardinalidad del producto cartesiano es el producto de las cardinalidades de sus factores, es decir, |R × S| = |R| × |S|.

Proyección (Π)

A proyección es una operación siniestra escrita como ${displaystyle Pi _{a_{1},ldotsa_{n}(R)}$ Donde ${displaystyle a_{1},ldotsa_{n}$ es un conjunto de nombres de atributos. El resultado de tal proyección se define como el conjunto que se obtiene cuando todos los tuples en R se restringen al conjunto ${displaystyle {a_{1},ldotsa_{n}}}$.

Nota: cuando se implementa en el estándar SQL, la "proyección predeterminada" devuelve un conjunto múltiple en lugar de un conjunto, y la proyección Π para eliminar datos duplicados se obtiene mediante la adición de la palabra clave DISTINCT.

Selección (σ)

A Selección generalizada es una operación siniestra escrita como ${displaystyle sigma _{varphi }(R)}$ Donde φ es una fórmula proposicional que consiste en átomos como se permite en la selección normal y los operadores lógicos ${displaystyle wedge }$ (y) ${displaystyle lor }$ o) y ${displaystyle neg }$ (negación). Esta selección selecciona todos esos tuples en R para la cual φ sostiene.

Para obtener una lista de todos los amigos o socios de negocios en un libro de direcciones, la selección puede ser escrita como ${displaystyle sigma _{text{isFriend = true},lor ,{text{isBusinessContacto = true}} {text{address}}}}$. El resultado sería una relación que contiene cada atributo de cada registro único donde isFriend es verdad o dónde isBusinessContact es verdad.

Renombrar (ρ)

A rename es una operación siniestra escrita como ${displaystyle rho _{a/b}(R)}$ donde el resultado es idéntico a R excepto que b atributo en todos los tuplas se renombra a un a atributo. Esto se utiliza simplemente para renombrar el atributo de una relación o la relación misma.

Para renombrar el atributo "isFriend" a "isBusinessContact" en una relación, ${displaystyle rho _{text{isBusinessContacto / isFriend} {text{addressBook}})}$ podría ser usado.

También hay ${displaystyle rho _{x(A_{1},ldotsA_{n}(R)}$ notación, donde R es renombrado a x y los atributos ${displaystyle {a_{1},ldotsa_{n}}}$ son renombrados a ${displaystyle {A_{1},ldots A_{n}$.

Operadores de uniones y similares

Unión natural (⋈)

La unión natural (⋈) es un operador binario que se escribe como (R ⋈ S) donde R y S son relaciones. El resultado de la unión natural es el conjunto de todas las combinaciones de tuplas en R y S que son iguales en sus nombres de atributos comunes. Por ejemplo, considere las tablas Employee y Dept y su unión natural:

Tenga en cuenta que ni la empleada llamada Mary ni el departamento de producción aparecen en el resultado.

Esto también se puede usar para definir la composición de las relaciones. Por ejemplo, la composición de Employee y Dept es su unión como se muestra arriba, proyectada en todos menos el atributo común DeptName. En la teoría de categorías, la unión es precisamente el producto de fibra.

La unión natural es posiblemente uno de los operadores más importantes, ya que es la contraparte relacional del operador lógico AND. Tenga en cuenta que si la misma variable aparece en cada uno de los dos predicados que están conectados por AND, entonces esa variable representa lo mismo y ambas apariencias siempre deben sustituirse por el mismo valor (esto es una consecuencia de la idempotencia del AND lógico). En particular, la unión natural permite la combinación de relaciones que están asociadas por una clave externa. Por ejemplo, en el ejemplo anterior, una clave foránea probablemente contiene desde Employee.DeptName a Dept.DeptName y luego la unión natural de Employee y Dept combina todos los empleados con sus departamentos. Esto funciona porque la clave externa se mantiene entre atributos con el mismo nombre. Si este no es el caso, como en la clave externa de Depto.Gerente a Empleado.Nombre entonces estos las columnas se deben renombrar antes de tomar la unión natural. Tal unión a veces también se denomina equijoin (ver θ-join).

Más formalmente, la semántica de la unión natural se define de la siguiente manera:

${displaystyle Rbowtie S=left{rcup svert rin Rland sin S\land {fnMitit {fnh} {fnMitit {fnh} {fnMitit} {fnh} {fnMitit} {fnh} {fnMitit {fnh} {fnMitit {fnHFF} {fnHFF} {fnHFF}}}}f}}}}fnMitf}}fnMitfnMitfnMitf}}fnMitf}fnMitfnMitf}fnMitf}}}}f}}}}fnMitf}}f}f}fnMitfnMitf}fnMitfnMitf}}fnMitfnMitfnMitf}fnKf}}f}f}}f}}}$

()1)

donde Fun(t) es un predicado que es verdadero para una relación t (en el sentido matemático) iff t es una función (es decir, t no asigna ningún atributo a varios valores). Por lo general, se requiere que R y S tengan al menos un atributo común, pero si se omite esta restricción, y R y S no tienen atributos comunes, entonces la unión natural se convierte exactamente en el producto cartesiano.

La unión natural se puede simular con las primitivas de Codd de la siguiente manera. Suponga que c₁,...,c_m son los nombres de atributo común a R y S, r₁,...,r< sub>n son los nombres de atributo únicos para R y s₁,...,s_k son los nombres de atributos exclusivos de S. Además, suponga que los nombres de atributo x₁,...,x_m no están ni en R ni en S. En un primer paso, los nombres de atributos comunes en S se pueden renombrar:

${displaystyle T=rho ¿Por qué? ¿Por qué? ¿Qué? ¿Qué?$

()2)

Luego tomamos el producto cartesiano y seleccionamos las tuplas que se van a unir:

${displaystyle P=sigma ¿Por qué? ¿Por qué? ¿Por qué? ¿Qué?$

()3)

Finalmente tomamos una proyección para deshacernos de los atributos renombrados:

${displaystyle ¿Qué?$

()4)

Θ-join y equijoin

Considere las tablas Automóvil y Barco que enumeran los modelos de automóviles y barcos y sus respectivos precios. Supongamos que un cliente quiere comprar un automóvil y un bote, pero no quiere gastar más dinero en el bote que en el automóvil. La combinación θ (⋈_θ) en el predicado CarPrice ≥ BoatPrice produce los pares aplanados de filas que satisfacen el predicado. Cuando se utiliza una condición en la que los atributos son iguales, por ejemplo, Precio, la condición se puede especificar como Precio=Precio o alternativamente (Precio) en sí mismo.

Para combinar tuples de dos relaciones donde la condición de combinación no es simplemente la igualdad de atributos compartidos es conveniente tener una forma más general de operador de la unión, que es la Silencio-join (o theta-join). El Silencio-join es un operador binario que está escrito como ${displaystyle {R bowtie S atop atheta b}$ o ${displaystyle {R bowtie S atop atheta v}$ Donde a y b son nombres de atributos, Silencio es un operador de relación binaria en el conjunto {Sea, ≤, =, √≥, √≥} . es una constante de valor, y R y S son relaciones. El resultado de esta operación consiste en todas las combinaciones de tuples en R y S que satisfacen Silencio. El resultado del Silencio- la unión se define sólo si los encabezados S y R son descompuestos, es decir, no contienen un atributo común.

Por lo tanto, la simulación de esta operación en las operaciones fundamentales es la siguiente:

R ⋈_Silencio S = σ_Silencio()R × S)

En caso de que el operador θ sea el operador de igualdad (=), esta unión también se denomina equijoin.

Tenga en cuenta, sin embargo, que un lenguaje informático que admita los operadores de unión y selección naturales no necesita la unión θ también, ya que esto se puede lograr mediante la selección del resultado de una unión natural (que degenera a producto cartesiano cuando no hay atributos compartidos).

En las implementaciones de SQL, la unión en un predicado generalmente se denomina unión interna, y la palabra clave on permite especificar el predicado utilizado para filtrar las filas. Es importante tener en cuenta: formar el producto cartesiano aplanado y luego filtrar las filas es conceptualmente correcto, pero una implementación usaría estructuras de datos más sofisticadas para acelerar la consulta de combinación.

Semiunión (⋉ y ⋊)

El semijoin izquierdo es una unión similar a la unión natural y escrito como ${displaystyle Rltimes S}$ Donde ${displaystyle R.$ y ${displaystyle S.$ son relaciones. El resultado es el conjunto de todos los tuples en ${displaystyle R.$ para el cual hay un tuple ${displaystyle S.$ que es igual en sus nombres de atributos comunes. La diferencia de una unión natural es que otras columnas de ${displaystyle S.$ no aparecen. Por ejemplo, considere los cuadros Employee y Dept y su semijoin:

Más formalmente, la semántica de la semiunión se puede definir como sigue:

${displaystyle Rltimes S={t:tin Rland exists sin S(operatorname {Fun} (tcup s)}$

Donde ${displaystyle operatorname {Fun} (r)}$ es como en la definición de la unión natural.

El semijoin se puede simular utilizando la unión natural como sigue. Si ${displaystyle a_{1},ldotsa_{n}$ son los nombres de los atributos ${displaystyle R.$, entonces

${displaystyle Rltimes S=Pi _{a_{1},ldotsa_{n}(Rbowtie S).}$

Puesto que podemos simular la unión natural con los operadores básicos, esto también es válido para la semiunión.

En el artículo de Codd de 1970, la semiunión se denomina restricción.

Antiunión (▷)

El antijoin, escrito como R ▷ S donde R y S son relaciones, es similar al semijoin, pero el resultado de un antijoin son solo aquellas tuplas en R para las cuales no tupla en S que es igual en su atributo común nombres

Por ejemplo, considere las tablas Employee y Dept y sus antijoin:

El antijoin se define formalmente de la siguiente manera:

R ▷ S = t: t ▪ R ∧ ¬s ▪ S()Diversión ()t ∪ s)}

o

R ▷ S = t: t ▪ R, no hay tuple s de S que satisfice Diversión ()t ∪ s)}

donde Fun (t ∪ s) es como en la definición de natural unirse.

La antiunión también se puede definir como el complemento de la semiunión, de la siguiente manera:

R ▷ S = R−R ⋉ S

()5)

Dado esto, el antijoin a veces se llama anti-semijoin, y el operador antijoin a veces se escribe como símbolo de semijoin con una barra encima, en lugar de ▷.

División (÷)

La división es una operación binaria que se escribe como R ÷ S. La división no se implementa directamente en SQL. El resultado consiste en las restricciones de tuplas en R a los nombres de atributos exclusivos de R, es decir, en el encabezado de R pero no en el cabecera de S, por lo que se cumple que todas sus combinaciones con tuplas en S están presentes en R. Para ver un ejemplo, vea las tablas Completed, DBProject y su división:

Si DBProject contiene todas las tareas del proyecto de base de datos, entonces el resultado de la división anterior contiene exactamente a los estudiantes que completaron ambas tareas en el proyecto de base de datos. Más formalmente, la semántica de la división se define de la siguiente manera:

R. S = t[a1,...an] t ▪ R ∧s ▪ S ()t[a1,...an] s) R)

()6)

donde {a₁,...,a_n} es el conjunto de nombres de atributos únicos para R y t[a₁,..., a_n] es la restricción de t a este conjunto. Por lo general, se requiere que los nombres de los atributos en el encabezado de S sean un subconjunto de los de R porque, de lo contrario, el resultado de la operación siempre estará vacío.

La simulación de la división con las operaciones básicas es la siguiente. Suponemos que a₁,...,a_n son el atributo nombres únicos para R y b₁,...,b_m son los nombres de los atributos de S. En el primer paso, proyectamos R en sus nombres de atributos únicos y construimos todas las combinaciones con tuplas en S:

T:= π_a1,...an()R) × S

En el ejemplo anterior, T representaría una tabla tal que cada Estudiante (porque Estudiante es la clave/atributo único de la tabla Completada) se combina con cada Tarea determinada. Entonces, Eugene, por ejemplo, tendría dos filas, Eugene → Base de datos1 y Eugene → Base de datos2 en T.

EG: Primero, finjamos que "Completed" tiene un tercer atributo llamado "grado". Es equipaje no deseado aquí, así que debemos proyectarlo siempre. De hecho en este paso podemos dejar caer "Task" de R también; el multiplicador lo vuelve a poner.

T:= π_Estudiante()R) × S // Esto nos da toda la combinación posible deseada, incluyendo aquellos que realmente no existen en R, y excluyendo otros (por ejemplo Fred TEN compilador1, que no es una combinación deseada)

En el siguiente paso restamos R de T

relación:

U:= T − R

En U tenemos lo posible combinaciones que "podrían tener" estado en R, pero no lo estaba.

EG: Otra vez con proyecciones — T y R necesidad de tener nombres/cabezas de atributos idénticos.

U:= T − π_{Estudiante,Task}()R) // Esto nos da una lista de "lo que falta".

Entonces, si ahora tomamos la proyección sobre los nombres de atributos exclusivos de R

entonces tenemos las restricciones de las tuplas en R para las cuales no todas las combinaciones con tuplas en S estaban presentes en R:

V:= π_a1,...an()U)

EG: Project U a sólo los atributos en cuestión (Estudiante)

V:= π_Estudiante()U)

Entonces, lo que queda por hacer es tomar la proyección de R en su nombres de atributos únicos y restar los de V:

W:= π_a1,...an()R) − V

EG: W:= π_Estudiante()R) − V.

Extensiones comunes

En la práctica, el álgebra relacional clásica descrita anteriormente se amplía con varias operaciones, como uniones externas, funciones agregadas e incluso cierre transitivo.

Uniones externas

& #34;llenar" valores para cada uno de los atributos del otro operando. Las uniones externas no se consideran parte del álgebra relacional clásica discutida hasta ahora.

Los operadores definidos en esta sección asumen la existencia de un valor null, ω, que no definimos, para ser usado para los valores de relleno; en la práctica esto corresponde a NULL en SQL. Para que las operaciones de selección posteriores en la tabla resultante sean significativas, se debe asignar un significado semántico a los nulos; en el enfoque de Codd, la lógica proposicional utilizada por la selección se extiende a una lógica de tres valores, aunque omitimos esos detalles en este artículo.

Se definen tres operadores de combinación externa: combinación externa izquierda, combinación externa derecha y combinación externa completa. (La palabra 'exterior' a veces se omite).

Unión externa izquierda (⟕)

La unión externa izquierda se escribe como R ⟕ S donde R y S son relaciones. El resultado de la combinación externa izquierda es el conjunto de todas las combinaciones de tuplas en R y S que son iguales en sus nombres de atributos comunes, además (en términos generales) de tuplas en R que no tienen tuplas coincidentes en S.

Como ejemplo, considere las tablas Employee y Dept y su combinación externa izquierda:

En la relación resultante, las tuplas en S que no tienen valores comunes en los nombres de atributos comunes con las tuplas en R toman un valor nulo, ω.

Dado que no hay tuplas en Dept con un NombreDept de Finanzas o Ejecutivo, ω s ocurren en la relación resultante donde las tuplas en Employee tienen un DeptName de Finanzas o Ejecutivo.

Sea r₁, r₂,..., r Sean _n los atributos de la relación R y sean {(ω,..., ω )} ser el singleton relación sobre los atributos que son únicos a la relación S (aquellos que no son atributos de R). Luego, la combinación externa izquierda se puede describir en términos de combinación natural (y, por lo tanto, utilizando operadores básicos) de la siguiente manera:

${displaystyle (Rbowtie S)cup (R-pi _{1},r_{2},dotsr_{n}}(Rbowtie S))times {(omegadotsomega)})}$

Unión externa derecha (⟖)

La combinación externa derecha se comporta de forma casi idéntica a la combinación externa izquierda, pero las funciones de las tablas se intercambian.

La unión externa derecha de las relaciones R y S se escribe como R ⟖ S. El resultado de la unión externa derecha es el conjunto de todas las combinaciones de tuplas en R y S que son iguales en sus nombres de atributos comunes, además de las tuplas en S que no tienen tuplas coincidentes en R.

Por ejemplo, considere las tablas Employee y Dept y sus unión externa derecha:

En la relación resultante, las tuplas en R que no tienen valores comunes en los nombres de atributos comunes con las tuplas en S toman un valor nulo, ω.

Dado que no hay tuplas en Employee con un DeptName de Production, ωs ocurren en el Nombre y los atributos EmpId de la relación resultante donde las tuplas en Dept tenían DeptName de Production.

Sea s₁, s₂,..., s Sean _n los atributos de la relación S y sea {(ω,..., ω )} ser el singleton relación sobre los atributos que son únicos a la relación R (aquellos que no son atributos de S). Luego, al igual que con la combinación externa izquierda, la combinación externa derecha se puede simular utilizando la combinación natural de la siguiente manera:

${displaystyle (Rbowtie S)cup ({(omegadotsomega)times (S-pi) ¿Qué?$

Unión externa completa (⟗)

La unión externa o la unión externa completa en efecto combina los resultados de las uniones externas izquierda y derecha.

La unión externa completa se escribe como R ⟗ S donde R y S son relaciones. El resultado de la combinación externa completa es el conjunto de todas las combinaciones de tuplas en R y S que son iguales en sus nombres de atributos comunes, además de las tuplas en S que no tienen tuplas coincidentes en R y tuplas en R que no tienen tuplas coincidentes en S en sus nombres de atributos comunes.

Por ejemplo, considere las tablas Employee y Dept y sus unión externa completa:

En la relación resultante, las tuplas en R que no tienen valores comunes en los nombres de atributos comunes con las tuplas en S toman un valor nulo, ω. Las tuplas en S que no tienen valores comunes en los nombres de atributos comunes con las tuplas en R también toman un valor nulo, ω.

La combinación externa completa se puede simular utilizando las combinaciones externas izquierda y derecha (y, por lo tanto, la combinación natural y la unión de conjuntos) de la siguiente manera:

R ⟗ S =R ⟕ S∪R ⟖ S)

Operaciones para cálculos de dominio

No se ha introducido nada en el álgebra relacional hasta ahora que permita cálculos en los dominios de datos (aparte de la evaluación de expresiones proposicionales que implican igualdad). Por ejemplo, no es posible usar solo el álgebra presentada hasta ahora para escribir una expresión que multiplique los números de dos columnas, p. un precio unitario con una cantidad para obtener un precio total. Los lenguajes de consulta prácticos tienen tales facilidades, p. SQL SELECT permite operaciones aritméticas para definir nuevas columnas en el resultado SELECT< /span> precio_unidad *< /span> cantidad AS< /span> precio_total DESDE< /span> t, y una instalación similar es proporcionada más explícitamente por la palabra clave EXTEND del Tutorial D. En teoría de bases de datos, esto se denomina proyección extendida.

Agregación

Además, calcular varias funciones en una columna, como la suma de sus elementos, tampoco es posible usando el álgebra relacional presentada hasta ahora. Hay cinco funciones agregadas que se incluyen con la mayoría de los sistemas de bases de datos relacionales. Estas operaciones son Suma, Cuenta, Promedio, Máximo y Mínimo. En álgebra relacional, la operación de agregación sobre un esquema (A₁, A₂,... A_n) se escribe de la siguiente manera:

${displaystyle G_{1},G_{2},ldots G_{m} g_{f_{1} {A_{1}'),f_{2}({A_{2}'),ldotsf_{k}({A_{k}')} (r)}$

donde cada A_j', 1 ≤ j ≤ k, es uno de los atributos originales A_i, 1 ≤ i ≤ n.

Los atributos que preceden a la g son atributos de agrupación, que funcionan como un "agrupar por" cláusula en SQL. Luego hay un número arbitrario de funciones de agregación aplicadas a atributos individuales. La operación se aplica a una relación arbitraria r. Los atributos de agrupación son opcionales y, si no se proporcionan, las funciones de agregación se aplican en toda la relación a la que se aplica la operación.

Supongamos que tenemos una tabla llamada Cuenta con tres columnas, a saber, Account_Number, Branch_Name y < span class="monospaced">Balance. Deseamos encontrar el saldo máximo de cada rama. Esto se logra con _{Branch_Name}G_Max(Balance)(Cuenta). Para encontrar el saldo más alto de todas las cuentas, independientemente de la sucursal, simplemente podríamos escribir G_Max(Saldo)(Cuenta).

La agrupación a menudo se escribe como _{Branch_Name}ɣ_{Max(Balance )}(Cuenta) en su lugar.

Cierre transitivo

Aunque el álgebra relacional parece lo suficientemente poderosa para la mayoría de los propósitos prácticos, existen algunos operadores simples y naturales en las relaciones que no pueden expresarse mediante el álgebra relacional. Uno de ellos es el cierre transitivo de una relación binaria. Dado un dominio D, sea la relación binaria R un subconjunto de D×D. La clausura transitiva R⁺ de R es el subconjunto más pequeño de D×D que contiene R y cumple la siguiente condición:

${displaystyle forall xforall yforall zleft(x,y)in R^{+}wedge (y,z)in R^{+}Rightarrow (x,z)in R^{+}right)}$

Se puede demostrar utilizando el hecho de que no existe una expresión de álgebra relacional E(R) tomando R como un argumento variable que produce R⁺.

Sin embargo, SQL admite oficialmente dichas consultas de puntos fijos desde 1999, y mucho antes tenía extensiones específicas del proveedor en esta dirección.

Uso de propiedades algebraicas para optimización de consultas

Los sistemas de administración de bases de datos relacionales a menudo incluyen un optimizador de consultas que intenta determinar la forma más eficiente de ejecutar una consulta determinada. Los optimizadores de consultas enumeran posibles planes de consulta, estiman su costo y seleccionan el plan con el costo estimado más bajo. Si las consultas están representadas por operadores del álgebra relacional, el optimizador de consultas puede enumerar posibles planes de consulta reescribiendo la consulta inicial utilizando las propiedades algebraicas de estos operadores.

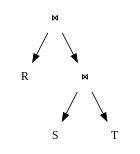
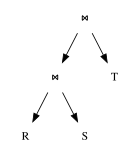
Las consultas se pueden representar como un árbol, donde

• los nodos internos son operadores,
• las hojas son relaciones,
• los subárboles son subexpresiones.

El objetivo principal del optimizador de consultas es transformar los árboles de expresión en árboles de expresión equivalentes, donde el tamaño promedio de las relaciones generadas por las subexpresiones en el árbol es menor que antes de la optimización. El objetivo secundario es tratar de formar subexpresiones comunes dentro de una sola consulta, o si se está evaluando más de una consulta al mismo tiempo, en todas esas consultas. La razón detrás del segundo objetivo es que basta con calcular las subexpresiones comunes una vez y los resultados se pueden usar en todas las consultas que contengan esa subexpresión.

Aquí hay un conjunto de reglas que se pueden usar en tales transformaciones.

Selección

Las reglas sobre los operadores de selección juegan el papel más importante en la optimización de consultas. La selección es un operador que reduce de manera muy efectiva el número de filas en su operando, por lo que si las selecciones en un árbol de expresión se mueven hacia las hojas, las relaciones internas (producidas por subexpresiones) probablemente se reducirán.

Propiedades básicas de selección

La selección es idempotente (múltiples aplicaciones de la misma selección no tienen ningún efecto adicional más allá de la primera) y conmutativa (el orden en que se aplican las selecciones no tiene efecto en el resultado final).

1. ${displaystyle sigma _{A}(R)=sigma _{A}sigma _{A}(R),!$
2. ${displaystyle sigma _{A}sigma _{B}(R)=sigma _{B}sigma _{A}(R),!$

Dividir selecciones con condiciones complejas

Una selección cuya condición es una conjunción de condiciones más simples es equivalente a una secuencia de selecciones con esas mismas condiciones individuales, y una selección cuya condición es una disyunción es equivalente a una unión de selecciones. Estas identidades se pueden usar para fusionar selecciones, de modo que sea necesario evaluar menos selecciones, o para dividirlas, de modo que las selecciones de componentes se puedan mover u optimizar por separado.

1. ${displaystyle sigma _{Aland B}(R)=sigma _{A}(sigma _{B}(R))=sigma _{B}(sigma _{A}(R)}$
2. ${displaystyle sigma _{Alor B}(R)=sigma _{A}(R)cup sigma _{B}(R)}$

Selección y producto cruzado

El producto cruzado es el operador más costoso para evaluar. Si las relaciones de entrada tienen N y M filas, el resultado contendrá ${displaystyle NM!$ filas. Por lo tanto, es importante disminuir el tamaño de ambos operandos antes de aplicar el operador de productos cruzados.

Esto se puede hacer eficazmente si el producto cruzado es seguido por un operador de selección, por ejemplo. ${displaystyle sigma _{A}(Rtimes P)}$. Considerando la definición de la unión, este es el caso más probable. Si el producto cruzado no es seguido por un operador de selección, podemos tratar de empujar una selección desde niveles más altos del árbol de expresión utilizando las otras reglas de selección.

En el caso anterior la condición A se rompe en condiciones B, C y D usando las reglas de división sobre condiciones de selección complejas, de modo que ${displaystyle A=Bwedge Cwedge D}$ y B contiene atributos sólo de R, C contiene atributos sólo de P, y D contiene la parte de A que contiene atributos de ambos R y P. Nota, que B, C o D posiblemente estén vacías. Luego se sostiene lo siguiente:

${displaystyle sigma _{A}(Rtimes P)=sigma ¿Por qué? _{D}(sigma _{B}(R)times sigma _{C}(P)}$

Operadores de selección y configuración

La selección es distributiva sobre los operadores de diferencia, intersección y unión de conjuntos. Las siguientes tres reglas se utilizan para empujar la selección debajo de las operaciones establecidas en el árbol de expresión. Para los operadores de diferencia de conjuntos y de intersección, es posible aplicar el operador de selección a uno solo de los operandos que siguen a la transformación. Esto puede ser beneficioso cuando uno de los operandos es pequeño y la sobrecarga de evaluar el operador de selección supera los beneficios de usar una relación más pequeña como operando.

1. ${displaystyle sigma _{A}(Rsetminus P)=sigma _{A}(R)setminus sigma _{A}(P)=sigma _{A}(R)setminus P}$
2. ${displaystyle sigma _{A}(Rcup P)=sigma _{A}(R)cup sigma _{A}(P)}$
3. ${displaystyle sigma _{A}(Rcap P)=sigma _{A}(R)cap sigma _{A}(P)=sigma _{A}(R)cap P=Rcap sigma _{A}(P)}$

Selección y proyección

La selección conmuta con la proyección si y solo si los campos a los que se hace referencia en la condición de selección son un subconjunto de los campos en la proyección. Realizar la selección antes de la proyección puede ser útil si el operando es un producto cruzado o una unión. En otros casos, si la condición de selección es relativamente costosa de calcular, mover la selección fuera de la proyección puede reducir el número de tuplas que deben probarse (ya que la proyección puede producir menos tuplas debido a la eliminación de duplicados resultantes de campos omitidos).

${displaystyle pi _{a_{1},ldotsa_{n}(sigma _{A}(R)=sigma _{A}(pi _{a_{1},ldotsa_{n}(R){text{ where fields in }Asubseteq{a_}{1}ldot}ldot} {i} {i} {i}i} {i} {i}{i}i}i} {i}i}{i}i}i}i}{i}i}i}i}i}i}i}i}{i}i}i}i}i}i}i}i}i}i}i}i}i}i}i}i}{i}i}i}i}i}i}i}i}i}$

Proyección

Propiedades básicas de proyección

La proyección es idempotente, por lo que una serie de proyecciones (válidas) es equivalente a la proyección más externa.

${displaystyle pi ################################################################################################################################################################################################################################################################$

Operadores de proyección y conjuntos

La proyección es distributiva sobre unión de conjuntos.

${displaystyle pi _{a_{1},ldotsa_{n}(Rcup P)=pi _{a_{1},ldotsa_{n}}(R)cup pi _{a__{1},ldotsa_{n}}(P).}$

La proyección no se distribuye sobre la intersección y la diferencia de conjuntos. Los contraejemplos vienen dados por:

${displaystyle pi _{A}(\langle A=a,B=brangle }cap {langle A=a,B=b'rangle })=emptyset }$

${displaystyle pi _{A}({langle A=a,B=brangle })cap pi _{A}({langle A=a,B=b'rangle })={langle A=arangle {}}$

y

${displaystyle pi _{langle A=a,B=brangle }setminus {langle A=a,B=b'rangle })={langle A=arangle {}}$

${displaystyle pi _{A}({langle A=a,B=brangle })setminus pi _{A}({\langle A=a,B=b'rangle })=emptyset ,}$

donde se supone que b es distinto de b'.

Renombrar

Propiedades básicas de cambio de nombre

Los cambios de nombre sucesivos de una variable se pueden colapsar en un solo cambio de nombre. Las operaciones de cambio de nombre que no tienen variables en común se pueden reordenar arbitrariamente entre sí, lo que se puede aprovechar para hacer que los cambios de nombre sucesivos sean adyacentes para que se puedan colapsar.

1. ${displaystyle rho _{a/b}(rho _{b/c}(R)=rho _{a/c}(R),!}$
2. ${displaystyle rho _{a/b}(rho _{c/d}(R)=rho _{c/d}(rho _{a/b}(R),!}$

Renombrar y establecer operadores

Renombrar es distributivo sobre diferencia, unión e intersección de conjuntos.

1. ${displaystyle rho _{a/b}(Rsetminus P)=rho _{a/b}(R)setminus rho _{a/b}(P)}$
2. ${displaystyle rho _{a/b}(Rcup P)=rho _{a/b}(R)cup rho _{a/b}(P)}$
3. ${displaystyle rho _{a/b}(Rcap P)=rho _{a/b}(R)cap rho _{a/b}(P)}$

Producto y unión

El producto cartesiano es distributivo sobre unión.

1. ${displaystyle (Atimes B)cup (Atimes C)=Atimes (Bcup C)}$

Implementaciones

El primer lenguaje de consulta basado en el álgebra de Codd fue Alpha, desarrollado por el propio Dr. Codd. Posteriormente, se creó ISBL, y este trabajo pionero ha sido aclamado por muchas autoridades por haber mostrado el camino para convertir la idea de Codd en un lenguaje útil. Business System 12 fue un DBMS relacional de corta duración y sólido en la industria que siguió el ejemplo de ISBL.

En 1998, Chris Date y Hugh Darwen propusieron un lenguaje llamado Tutorial D diseñado para usarse en la enseñanza de la teoría de bases de datos relacionales, y su lenguaje de consulta también se basa en las ideas de ISBL. Rel es una implementación del Tutorial D.

Incluso el lenguaje de la consulta de SQL se basa ligeramente en un álgebra relacional, aunque los operados en SQL (tablas) no son exactamente relaciones y varios teoremas útiles sobre el álgebra relacional no se sostienen en la contraparte SQL (arguiblemente en detrimento de optimistas y/o usuarios). El modelo de tabla SQL es una bolsa (multiset), en lugar de un conjunto. Por ejemplo, la expresión ${displaystyle (Rcup S)setminus T=(Rsetminus T)cup (Ssetminus T)}$ es un teorema para álgebra relacional en conjuntos, pero no para álgebra relacional en bolsas; para un tratamiento de álgebra relacional en bolsas ver capítulo 5 del libro de texto "Completo" de García-Molina, Ullman y Sabiduría.