Álgebra geométrica

ImprimirCitar

Estructura algebraica diseñada para geometría

En matemáticas, un álgebra geométrica (también conocida como álgebra real de Clifford) es una extensión del álgebra elemental para trabajar con objetos geométricos como vectores. El álgebra geométrica se construye a partir de dos operaciones fundamentales, la suma y el producto geométrico. La multiplicación de vectores da como resultado objetos de mayor dimensión llamados multivectores. En comparación con otros formalismos para manipular objetos geométricos, el álgebra geométrica se destaca por admitir la división de vectores y la suma de objetos de diferentes dimensiones.

El producto geométrico fue mencionado brevemente por primera vez por Hermann Grassmann, quien estaba principalmente interesado en desarrollar el álgebra exterior estrechamente relacionada. En 1878, William Kingdon Clifford amplió enormemente el trabajo de Grassmann para formar lo que ahora se suele llamar álgebras de Clifford en su honor (aunque el propio Clifford optó por llamarlas "álgebras geométricas"). Clifford definió el álgebra de Clifford y su producto como una unificación del álgebra de Grassmann y el álgebra de cuaterniones de Hamilton. Agregar el producto exterior dual de Grassmann (el 'encuentro') permite el uso del álgebra de Grassmann-Cayley, y una versión conforme de este último junto con un álgebra conforme de Clifford produce un álgebra geométrica conforme que proporciona un marco para geometrías clásicas. En la práctica, estas y varias operaciones derivadas permiten una correspondencia de elementos, subespacios y operaciones del álgebra con interpretaciones geométricas. Durante varias décadas, el álgebra geométrica fue algo ignorada, eclipsada en gran medida por el cálculo vectorial desarrollado recientemente para describir el electromagnetismo. El término "álgebra geométrica" fue repopularizado en la década de 1960 por Hestenes, quien abogó por su importancia para la física relativista.

Los escalares y vectores tienen su interpretación habitual, y componen subespacios distintos de un álgebra geométrica. Los conductores proporcionan una representación más natural de las cantidades pseudovectoras en álgebra vectorial como área orientada, ángulo orientado de rotación, torque, impulso angular y el campo electromagnético. Un trivector puede representar un volumen orientado, y así sucesivamente. Un elemento llamado hoja se puede utilizar para representar un subespacio $V$ y proyecciones ortogonales sobre ese subespacio. Las rotaciones y reflexiones están representadas como elementos. A diferencia de un álgebra vectorial, un álgebra geométrica naturalmente alberga cualquier número de dimensiones y cualquier forma cuadrática como en relatividad.

Ejemplos de álgebras geométricas aplicadas en física incluyen el álgebra del espacio-tiempo (y el álgebra menos común del espacio físico) y el álgebra geométrica conforme. El cálculo geométrico, una extensión de AG que incorpora diferenciación e integración, se puede utilizar para formular otras teorías, como el análisis complejo y la geometría diferencial, p. usando el álgebra de Clifford en lugar de formas diferenciales. El álgebra geométrica ha sido defendida, sobre todo por David Hestenes y Chris Doran, como el marco matemático preferido para la física. Los defensores afirman que proporciona descripciones compactas e intuitivas en muchas áreas, incluidas la mecánica clásica y cuántica, la teoría electromagnética y la relatividad. GA también ha encontrado uso como herramienta computacional en gráficos por computadora y robótica.

Definición y notación

Hay varias maneras diferentes de definir un álgebra geométrica. El enfoque original de Hestenes fue axiomático, "lleno de significado geométrico" y equivalente al álgebra universal Clifford. Dado un espacio cuadrático finito-dimensional $V$ sobre un terreno $F$ con una forma bilineal simétrica (la producto interior, por ejemplo la métrica Euclidean o Lorentziana) ${displaystyle g:Vtimes Vto F}$ , el álgebra geométrica para este espacio cuadrático es el álgebra Clifford ${displaystyle operatorname {Cl} (V,g)}$ . Como siempre en este dominio, para el resto de este artículo, sólo el caso real, ${displaystyle F=mathbb {R} }$ , será considerado. La notación ${displaystyle {mathcal {G}}(p,q)}$ (respectivamente ${displaystyle {mathcal {G}}(p,q,r)}$ ) se utilizará para denotar un álgebra geométrica para el cual la forma bilinear $g$ tiene la firma $(p,q)$ (respectivamente ${displaystyle (p,q,r)}$ ).

El producto esencial en el álgebra se llama el producto geométrico, y el producto en el álgebra exterior contenida se llama el producto exterior (frecuentemente llamado producto de cuña y menos a menudo producto exterior). Es estándar denotar estos respectivamente por yuxtaposición (es decir, suprimir cualquier símbolo de multiplicación explícita) y el símbolo $wedge$ . La definición anterior del álgebra geométrica es abstracta, por lo que resumimos las propiedades del producto geométrico por el siguiente conjunto de axiomas. El producto geométrico tiene las siguientes propiedades, para ${displaystyle A,B,Cin {mathcal {G}}(p,q)}$ :

${displaystyle ABin {mathcal {G}}(p,q)}$ (cerrado)
${displaystyle 1A=A1=A}$ , donde $1$ es el elemento de identidad (existencia de un elemento de identidad)
$A(BC)=(AB)C$ (asociatividad)
$A(B+C)=AB+AC$ y $(B+C)A=BA+CA$ (distributividad)
${displaystyle a^{2}=g(a,a)1}$ , donde $a$ es cualquier elemento del subespacio $V$ del álgebra.

El producto exterior tiene las mismas propiedades, excepto que la última propiedad anterior es reemplazada por ${displaystyle awedge a=0}$ para $ain V$ .

Tenga en cuenta que en la última propiedad arriba, el número real ${displaystyle g(a,a)}$ no ser negativo si $g$ no es positivo-definido. Una propiedad importante del producto geométrico es la existencia de elementos que tienen un inverso multiplicativo. Para un vector $a$ , si ${displaystyle a^{2}neq 0}$ entonces $a^{-1}$ existe y es igual a ${displaystyle g(a,a)^{-1}a}$ . Un elemento no cero del álgebra no necesariamente tiene un inverso multiplicativo. Por ejemplo, si $u$ es un vector en $V$ tales que $u^{2}=1$ , el elemento ${displaystyle textstyle {frac {1}{2}}(1+u)}$ es un elemento idempotente notrivial y un divisor no cero, y por lo tanto no tiene inverso.

Es habitual identificar $mathbb {R}$ y $V$ con sus imágenes bajo las incrustaciones naturales ${displaystyle mathbb {R} to {mathcal {G}}(p,q)}$ y ${displaystyle Vto {mathcal {G}}(p,q)}$ . En este artículo se asume esta identificación. A lo largo de todo, los términos scalar y vector referencia a elementos $mathbb {R}$ y $V$ respectivamente (y de sus imágenes bajo esta incrustación).

El producto geométrico

Dados dos vectores

a

b

, si el producto geométrico

ab

es anticommutante; son perpendiculares (top) porque

{displaystyle acdot b=0}

, si es conmutativo; son paralelos (abajo) porque

{displaystyle awedge b=0}

Orientación definida por un conjunto ordenado de vectores.

La orientación inversa corresponde a la negación del producto exterior.

Interpretación geométrica de grado-

n

elementos en un álgebra exterior real para

n=0

(punto firmado),

1

(segmento de línea directa, o vector),

2

(elemento plano orientado),

3

(volumen orientado). El producto exterior de

n

vectores se pueden visualizar como cualquier

n

- forma dimensional (por ejemplo.

n

- Parallelotope,

n

-ellipsoid); con magnitud (hipervolume), y orientación definida por eso en su

(n-1)

- límites dimensionales y en qué lado está el interior.

Para vectores $a$ y $b$ , podemos escribir el producto geométrico de cualquier dos vectores $a$ y $b$ como la suma de un producto simétrico y un producto antisimétrico:

{displaystyle ab={frac {1}{2}}(ab+ba)+{frac {1}{2}}(ab-ba)}

Así podemos definir el producto interior de vectores como

{displaystyle acdot b:=g(a,b),}

para que el producto simétrico se pueda escribir como

{displaystyle {frac {1}{2}}(ab+ba)={frac {1}{2}}left((a+b)^{2}-a^{2}-b^{2}right)=acdot b}

Por el contrario, $g$ está completamente determinado por el álgebra. La parte antisimétrica es el producto exterior de los dos vectores, el producto del álgebra exterior contenida:

awedge b:={frac {1}{2}}(ab-ba)=-(bwedge a)

Entonces por simple suma:

{displaystyle ab=acdot b+awedge b}

la forma nogeneralizada o vectorial del producto geométrico.

Los productos interiores y exteriores están asociados con conceptos familiares de álgebra vectorial estándar. Geométricamente, $a$ y $b$ son paralelos si su producto geométrico es igual a su producto interior, mientras que $a$ y $b$ son perpendiculares si su producto geométrico es igual a su producto exterior. En un álgebra geométrica para el cual el cuadrado de cualquier vector no cero es positivo, el producto interno de dos vectores se puede identificar con el producto punto de álgebra vectorial estándar. El producto exterior de dos vectores se puede identificar con el área firmada encerrada por un paralelograma cuyos lados son los vectores. El producto cruzado de dos vectores en $3$ dimensiones con forma cuadrática definitiva positiva está estrechamente relacionada con su producto exterior.

La mayoría de las instancias de álgebras geométricas de interés tienen una forma cuadrática no degenerada. Si la forma cuadrática es completamente degenerada, el producto interno de dos vectores cualesquiera es siempre cero, y el álgebra geométrica es simplemente un álgebra exterior. A menos que se indique lo contrario, este artículo tratará solo álgebras geométricas no degeneradas.

El producto exterior se extiende naturalmente como un operador binario bilineal asociativo entre dos elementos cualquiera del álgebra, satisfaciendo las identidades

{displaystyle {begin{aligned}1wedge a_{i}&=a_{i}wedge 1=a_{i}\a_{1}wedge a_{2}wedge cdots wedge a_{r}&={frac {1}{r!}}sum _{sigma in {mathfrak {S}}_{r}}operatorname {sgn} (sigma)a_{sigma (1)}a_{sigma (2)}cdots a_{sigma (r)},end{aligned}}}

donde la suma está sobre todas las permutaciones de los índices, con $operatorname {sgn} (sigma)$ el signo de la permutación, y $a_{i}$ son vectores (no elementos generales del álgebra). Puesto que cada elemento del álgebra se puede expresar como la suma de productos de esta forma, esto define el producto exterior para cada par de elementos del álgebra. Se deriva de la definición que el producto exterior forma un álgebra alterna.

Hojas, grados y base canónica

Un multivector que es el producto exterior $r$ vectores linealmente independientes se llama un hoja, y se dice que es de grado $r$ . Un multivector que es la suma de cuchillas de grado $r$ se llama un (homogéneo) multivector de grado $r$ . Desde los axiomas, con cierre, cada multivector del álgebra geométrica es una suma de cuchillas.

Considerar un conjunto de $r$ vectores linealmente independientes ${displaystyle {a_{1},ldotsa_{r}}}$ azotando un $r$ - subespacial dimensional del espacio vectorial. Con estos, podemos definir una matriz simétrica real (de la misma manera que una matriz gramiana)

{displaystyle [mathbf {A} ]_{ij}=a_{i}cdot a_{j}}

Por el teorema espectral, $mathbf {A}$ se puede diagonalizar a la matriz diagonal $mathbf{D}$ por una matriz ortogonal ${displaystyle mathbf {O} }$ via

sum _{k,l}[mathbf {O} ]_{ik}[mathbf {A} ]_{kl}[mathbf {O} ^{mathrm {T} }]_{lj}=sum _{k,l}[mathbf {O} ]_{ik}[mathbf {O} ]_{jl}[mathbf {A} ]_{kl}=[mathbf {D} ]_{ij}

Define un nuevo conjunto de vectores ${displaystyle {e_{1},ldotse_{r}}}$ , conocido como vectores de base ortogonal, para ser los transformados por la matriz ortogonal:

e_{i}=sum _{j}[mathbf {O} ]_{ij}a_{j}

Puesto que las transformaciones ortogonales preservan los productos interiores, sigue que $e_{i}cdot e_{j}=[mathbf {D} ]_{ij}$ y así ${displaystyle {e_{1},ldotse_{r}}}$ son perpendiculares. En otras palabras, el producto geométrico de dos vectores distintos $e_{i}neq e_{j}$ está completamente especificado por su producto exterior, o más generalmente

{displaystyle {begin{array}{rl}e_{1}e_{2}cdots e_{r}&=e_{1}wedge e_{2}wedge cdots wedge e_{r}\&=left(sum _{j}[mathbf {O} ]_{1j}a_{j}right)wedge left(sum _{j}[mathbf {O} ]_{2j}a_{j}right)wedge cdots wedge left(sum _{j}[mathbf {O} ]_{rj}a_{j}right)\&=(det mathbf {O})a_{1}wedge a_{2}wedge cdots wedge a_{r}end{array}}}

Por lo tanto, cada hoja de grado $r$ puede ser escrito como un producto geométrico $r$ vectores. Más generalmente, si se permite un álgebra geométrica degenerada, entonces la matriz ortogonal es reemplazada por una matriz de bloque que es ortogonal en el bloque nondegenerado, y la matriz diagonal tiene entradas de valor cero a lo largo de las dimensiones degeneradas. Si los nuevos vectores del subespacio nodegenerado se normalizan según

{hat {e}}_{i}={frac {1}{sqrt {|e_{i}cdot e_{i}|}}}e_{i},

entonces estos vectores normalizados deben cuadrado a $+1$ o $-1$ . Por la ley de inercia de Sylvester, el número total de $+1$ s y el número total de $-1$ s a lo largo de la matriz diagonal es invariante. Por extensión, el número total $p$ de estos vectores que cuadran a $+1$ y el número total $q$ ese cuadrado a $-1$ es invariante. (El número total de vectores de base que cuadrado a cero también es invariable, y puede ser no cero si se permite el caso degenerado). Denotamos este álgebra ${mathcal {G}}(p,q)$ . Por ejemplo, ${mathcal {G}}(3,0)$ modelos tridimensionales Espacio euclidiano, ${mathcal {G}}(1,3)$ tiempo espacial relativista y ${mathcal {G}}(4,1)$ a álgebra geométrica conformal de un espacio tridimensional.

El conjunto de todos los productos posibles de $n$ vectores de base ortogonal con índices en orden creciente, incluyendo $1$ como el producto vacío, forma una base para todo el álgebra geométrica (una analogía del teorema PBW). Por ejemplo, lo siguiente es una base para el álgebra geométrica ${mathcal {G}}(3,0)$ :

{displaystyle {1,e_{1},e_{2},e_{3},e_{1}e_{2},e_{2}e_{3},e_{3}e_{1},e_{1}e_{2}e_{3}}}

Una base formada de esta manera se llama base canónica para el álgebra geométrica, y cualquier otra base ortogonal para $V$ producirá otra base canónica. Cada base canónica consiste en $2^{n}$ elementos. Cada multivector del álgebra geométrica se puede expresar como una combinación lineal de los elementos de base canónica. Si los elementos de base canónica son ${displaystyle {B_{i}mid iin S}}$ con $S$ siendo un conjunto de índice, entonces el producto geométrico de cualquier dos multivectores es

{displaystyle left(sum _{i}alpha _{i}B_{i}right)left(sum _{j}beta _{j}B_{j}right)=sum _{i,j}alpha _{i}beta _{j}B_{i}B_{j}.}

La terminología " $k$ -vector" se encuentra a menudo para describir multivectores que contienen elementos de sólo un grado. En el espacio dimensional superior, algunos de estos multivectores no son cuchillas (no se puede considerar en el producto exterior de $k$ vectores). Por ejemplo, ${displaystyle e_{1}wedge e_{2}+e_{3}wedge e_{4}}$ dentro ${displaystyle {mathcal {G}}(4,0)}$ no se puede tener en cuenta; normalmente, sin embargo, tales elementos del álgebra no ceden a la interpretación geométrica como objetos, aunque pueden representar cantidades geométricas tales como rotaciones. Sólo ${displaystyle 0,1,(n-1)}$ y $n$ - Los vencedores siempre son cuchillas $n$ - espacio.

Proyección de calificaciones

Utilizando una base ortogonal, se puede establecer una estructura espacial vectorial de grado. Elementos del álgebra geométrica que son múltiplos de escalar $1$ son de grado. ${displaystyle 0}$ cuchillas y se llaman scalars. Multivectores que están en el lapso de ${e_{1},ldotse_{n}}$ son de grado. $1$ cuchillas y son los vectores ordinarios. Multivectores en el lapso de $<math alttext="{displaystyle {e_{i}e_{j}mid 1leq i{}eiej▪ ▪ 1≤ ≤ i.j≤ ≤ n}{displaystyle # {e_{i}e_{j}mid 1leq i donejleq n}<img alt="{e_{i}e_{j}mid 1leq i$ son de grado. $2$ Las espadas y los bivectores. Esta terminología continúa hasta el último grado de $n$ - Véctores. Alternativamente, grado- $n$ cuchillas se llaman pseudoscalares, grado- $(n-1)$ Hojas pseudovectores, etc. Muchos de los elementos del álgebra no están calificados por este esquema ya que son sumas de elementos de grado diferente. Se dice que esos elementos son de grado mixto. La clasificación de los multivectores es independiente de la base elegida originalmente.

Esto es una clasificación como un espacio vectorial, pero no como álgebra. Porque el producto de un $r$ - negro y un $s$ - La hoja está contenida en el lapso ${displaystyle 0}$ a través de ${displaystyle r+s}$ -negros, el álgebra geométrica es un álgebra filtrada.

Un multivector $A$ puede ser descompuesto con Operador de proyección de grado $langle Arangle _{r}$ , que produce el grado- $r$ porción de $A$ . Como resultado:

A=sum _{r=0}^{n}langle Arangle _{r}

Como ejemplo, el producto geométrico de dos vectores $ab=acdot b+awedge b=langle abrangle _{0}+langle abrangle _{2}$ desde entonces ${displaystyle langle abrangle _{0}=acdot b}$ y ${displaystyle langle abrangle _{2}=awedge b}$ y ${displaystyle langle abrangle _{i}=0}$ , para $i$ de otros ${displaystyle 0}$ y $2$ .

La descomposición de un multivector $A$ también se pueden dividir en los componentes que son uniformes y los que son extraños:

{displaystyle A^{+}=langle Arangle _{0}+langle Arangle _{2}+langle Arangle _{4}+cdots }

{displaystyle A^{-}=langle Arangle _{1}+langle Arangle _{3}+langle Arangle _{5}+cdots }

Este es el resultado de olvidar la estructura de un ${mathrm {Z}}$ - espacio vectorial degradado ${displaystyle mathrm {Z} _{2}}$ - espacio vectorial degradado. El producto geométrico respeta esta calificación más gruesa. Así, además de ser un ${displaystyle mathrm {Z} _{2}}$ - espacio vectorial degradado, el álgebra geométrica es un ${displaystyle mathrm {Z} _{2}}$ - álgebra de grado o superálgebra.

Restricting to the even part, the product of two even elements is also even. Esto significa que incluso los multivectores definen un incluso subalgebra. El incluso subalgebra de un $n$ - álgebra geométrica dimensional es isomorfa (sin preservar ni filtración ni graduación) a un álgebra geométrica completa $(n-1)$ dimensiones. Ejemplos incluyen ${displaystyle {mathcal {G}}^{+}(2,0)cong {mathcal {G}}(0,1)}$ y ${displaystyle {mathcal {G}}^{+}(1,3)cong {mathcal {G}}(3,0)}$ .

Representación de subespacios

Álgebra geométrica representa subespacios de $V$ como cuchillas, y así coexisten en el mismo álgebra con vectores de $V$ . A $k$ - subespacial dimensional $W$ de $V$ está representado por tomar una base ortogonal ${displaystyle {b_{1},b_{2},ldotsb_{k}}}$ y el uso del producto geométrico para formar la hoja ${displaystyle D=b_{1}b_{2}cdots b_{k}}$ . Hay múltiples cuchillas que representan $W$ ; todos los representantes $W$ son múltiples escalar de $D$ . Estas cuchillas se pueden separar en dos conjuntos: múltiples positivos $D$ y múltiples negativos de $D$ . Los múltiplos positivos de $D$ se dice que la misma orientación como $D$ , y los múltiples negativos orientación opuesta.

Las hojas son importantes ya que las operaciones geométricas como proyecciones, rotaciones y reflexiones dependen de la factorabilidad a través del producto exterior que (la clase restringida de) $n$ -Las hojas proporcionan pero eso (la clase generalizada de) grado- $n$ multivectores no cuando ${displaystyle ngeq 4}$ .

Pseudoescalares unitarios

Unidad pseudoscalars son cuchillas que juegan roles importantes en GA. A unidad pseudoscalar para un subespacial no degenerado $W$ de $V$ es una hoja que es el producto de los miembros de una base ortonormal para $W$ . Se puede demostrar que si $I$ y $I'$ son ambos pseudoscalares unidad para $W$ , entonces ${displaystyle I=pm I'}$ y ${displaystyle I^{2}=pm 1}$ . Si uno no elige una base ortonormal para $W$ , entonces la incrustación Plücker da un vector en el álgebra exterior pero sólo hasta escalar. Utilizando el isomorfismo del espacio vector entre el álgebra geométrica y el álgebra exterior, esto da la clase de equivalencia ${displaystyle alpha I}$ para todos $alpha neq 0$ . La ortonormalidad se deshace de esta ambigüedad excepto los signos anteriores.

Suponga el álgebra geométrica ${mathcal {G}}(n,0)$ con el producto interno definido positivo familiar en $mathbb {R} ^{n}$ se forma. Dado un plano (subespacial bidimensional) $mathbb {R} ^{n}$ , uno puede encontrar una base ortonormal ${displaystyle {b_{1},b_{2}}}$ atravesando el avión, y así encontrar una unidad pseudoscalar ${displaystyle I=b_{1}b_{2}}$ representando a este avión. El producto geométrico de cualquier dos vectores en el lapso de $b_{1}$ y $b_{2}$ mentiras ${displaystyle {alpha _{0}+alpha _{1}Imid alpha _{i}in mathbb {R} }}$ , es decir, es la suma de una ${displaystyle 0}$ -vector y un $2$ - Doctor.

Por las propiedades del producto geométrico, ${displaystyle I^{2}=b_{1}b_{2}b_{1}b_{2}=-b_{1}b_{2}b_{2}b_{1}=-1}$ . El parecido a la unidad imaginaria no es incidental: el subespacial ${displaystyle {alpha _{0}+alpha _{1}Imid alpha _{i}in mathbb {R} }}$ es $mathbb {R}$ -algebra isomorfa a los números complejos. De esta manera, una copia de los números complejos está incrustada en el álgebra geométrica para cada subespacio bidimensional de $V$ sobre la cual la forma cuadrática es definida.

A veces es posible identificar la presencia de una unidad imaginaria en una ecuación física. Tales unidades surgen de una de las muchas cantidades en el álgebra real que cuadrado a $-1$ , y estos tienen significado geométrico debido a las propiedades del álgebra y la interacción de sus diversos subespacios.

In ${mathcal {G}}(3,0)$ , un caso familiar más ocurre. Dada una base canónica consistente en vectores ortonormales $e_{i}$ de $V$ , el conjunto de Todos $2$ - Los vencedores son azotados por

{displaystyle {e_{3}e_{2},e_{1}e_{3},e_{2}e_{1}}.}

Labelling these $i$ , $j$ y $k$ (Momentariamente desviando de nuestra convención de mayúsculas), el subespacio generado por ${displaystyle 0}$ -vectores y $2$ - Los ganadores son exactamente ${displaystyle {alpha _{0}+ialpha _{1}+jalpha _{2}+kalpha _{3}mid alpha _{i}in mathbb {R} }}$ . Este conjunto se ve como el subalgebra incluso de ${mathcal {G}}(3,0)$ , y además es isomorfo como $mathbb {R}$ - álgebra a las cuaterniones, otro importante sistema algebraico.

Extensiones de los productos interior y exterior

Es una práctica común extender el producto exterior de vectores a todo el álgebra. Esto se puede hacer mediante el uso del operador de proyección de grado mencionado anteriormente:

Cwedge D:=sum _{r,s}langle langle Crangle _{r}langle Drangle _{s}rangle _{r+s}

(producto exterior)

Esta generalización es consistente con la definición anterior que implica la antisimetrización. Otra generalización relacionada con el producto exterior es el producto conmutador:

Ctimes D:={tfrac {1}{2}}(CD-DC)

(producto conmutador)

El producto regresivo (generalmente denominado "meet") es el doble del producto exterior (o "join" en este contexto). La especificación dual de elementos permite, para cuchillas $A$ y $B$ , la intersección (o reunión) donde se debe tomar la dualidad en relación con la hoja de grado más pequeño que contiene ambos $A$ y $B$ (la unión).

{displaystyle Cvee D:=((CI^{-1})wedge (DI^{-1}))I}

con $I$ la unidad pseudoscalar del álgebra. El producto regresivo, como el producto exterior, es asociativo.

El producto interno de vectores también se puede generalizar, pero en más de una forma no equivalente. El documento (Dorst 2002) brinda un tratamiento completo de varios productos internos diferentes desarrollados para álgebras geométricas y sus interrelaciones, y la notación se toma de allí. Muchos autores usan el mismo símbolo que para el producto interno de vectores para su extensión elegida (por ejemplo, Hestenes y Perwass). No ha surgido una notación consistente.

Entre estas varias generalizaciones diferentes del producto interior en vectores están:

{displaystyle C;rfloor ;D:=sum _{r,s}langle langle Crangle _{r}langle Drangle _{s}rangle _{s-r}}

(contracción izquierda)

{displaystyle C;lfloor ;D:=sum _{r,s}langle langle Crangle _{r}langle Drangle _{s}rangle _{r-s}}

(contracción derecha)

{displaystyle C*D:=sum _{r,s}langle langle Crangle _{r}langle Drangle _{s}rangle _{0}}

(producto escalar)

{displaystyle Cbullet D:=sum _{r,s}langle langle Crangle _{r}langle Drangle _{s}rangle _{|s-r|}}

(el producto "(grasa) punto")

Dorst (2002) argumenta a favor del uso de contracciones en lugar del producto interno de Hestenes; son algebraicamente más regulares y tienen interpretaciones geométricas más limpias. Varias identidades que incorporan las contracciones son válidas sin restricción de sus entradas. Por ejemplo,

{displaystyle C;rfloor ;D=(Cwedge (DI^{-1}))I}

{displaystyle C;lfloor ;D=I((I^{-1}C)wedge D)}

{displaystyle (Awedge B)*C=A*(B;rfloor ;C)}

{displaystyle C*(Bwedge A)=(C;lfloor ;B)*A}

{displaystyle A;rfloor ;(B;rfloor ;C)=(Awedge B);rfloor ;C}

{displaystyle (A;rfloor ;B);lfloor ;C=A;rfloor ;(B;lfloor ;C).}

Beneficios de usar la contracción izquierda como extensión del producto interno en vectores incluyen que la identidad $ab=acdot b+awedge b$ se prorroga hasta ${displaystyle aB=a;rfloor ;B+awedge B}$ para cualquier vector $a$ y multivector $B$ , y que la operación de proyección ${mathcal {P}}_{b}(a)=(acdot b^{-1})b$ se prorroga hasta ${displaystyle {mathcal {P}}_{B}(A)=(A;rfloor ;B^{-1});rfloor ;B}$ para cualquier hoja $B$ y cualquier multivector $A$ (con una modificación menor para acomodar null $B$ , dado a continuación).

Base doble

Vamos ${displaystyle {e_{1},ldotse_{n}}}$ ser una base de $V$ , es decir, un conjunto de $n$ vectores linealmente independientes que abarcan los $n$ -dimensional espacio vectorial $V$ . La base que es dual a ${displaystyle {e_{1},ldotse_{n}}}$ es el conjunto de elementos del espacio vectorial dual ${displaystyle V^{*}}$ que forma un sistema biorthogonal con esta base, siendo así los elementos denotados ${displaystyle {e^{1},ldotse^{n}}}$ satisfacción

e^{i}cdot e_{j}=delta ^{i}{}_{j},

Donde $delta$ es el Kronecker delta.

Dada una forma cuadrática no degenerada $V$ , ${displaystyle V^{*}}$ se identifica naturalmente con $V$ , y la base dual puede considerarse como elementos $V$ , pero no son en general el mismo conjunto que la base original.

Teniendo en cuenta además una serie de $V$ , vamos

{displaystyle I=e_{1}wedge cdots wedge e_{n}}

ser el pseudoscalar (que no necesariamente cuadra a $pm 1$ ) formado de la base ${displaystyle {e_{1},ldotse_{n}}}$ . Los vectores de base dual pueden ser construidos como

{displaystyle e^{i}=(-1)^{i-1}(e_{1}wedge cdots wedge {check {e}}_{i}wedge cdots wedge e_{n})I^{-1},}

Donde ${check {e}}_{i}$ denota que el $i$ el vector base se omite del producto.

Una base dual también se conoce como base recíproca o marco recíproco.

Un uso importante de una base dual es separar vectores en componentes. Dado un vector $a$ , componentes de escalar $a^i$ puede definirse como

{displaystyle a^{i}=acdot e^{i}}

en términos de los cuales $a$ puede ser separado en componentes vectoriales como

{displaystyle a=sum _{i}a^{i}e_{i}.}

También podemos definir componentes de escalar $a_{i}$ como

{displaystyle a_{i}=acdot e_{i}}

en términos de los cuales $a$ puede ser separado en componentes vectoriales en términos de la base dual como

{displaystyle a=sum _{i}a_{i}e^{i}.}

Una base dual como se definió anteriormente para el subespacio vectorial de un álgebra geométrica puede extenderse para cubrir toda el álgebra. Por razones de compacidad, usaremos una sola letra mayúscula para representar un conjunto ordenado de índices vectoriales. es decir, escribiendo

{displaystyle J=(j_{1},dotsj_{n})}

Donde $<math alttext="{displaystyle j_{1}<j_{2}<dots j1.j2.⋯ ⋯ .jn,{displaystyle j_{1} seleccionj_{2}<img alt="{displaystyle j_{1}<j_{2}<dots$ podemos escribir una hoja de base como

{displaystyle e_{J}=e_{j_{1}}wedge e_{j_{2}}wedge cdots wedge e_{j_{n}}.}

La cuchilla recíproca correspondiente tiene los índices en orden opuesto:

{displaystyle e^{J}=e^{j_{n}}wedge cdots wedge e^{j_{2}}wedge e^{j_{1}}.}

Al igual que en el caso anterior con los vectores, se puede demostrar que

{displaystyle e^{J}*e_{K}=delta _{K}^{J}}

Donde $*$ es el producto del cuero cabelludo.

Con $A$ un multivector, ahora podemos definir componentes de escalar como

{displaystyle A^{J}=A*e^{J}}

en términos de los cuales $A$ se pueden separar en cuchillas de componentes como

{displaystyle A=sum _{J}A^{J}e_{J}.}

Podemos definir alternativamente los componentes de escalar ${displaystyle A_{J}}$ como

{displaystyle A_{J}=A*e_{J}}

en términos de los cuales $A$ se pueden separar en cuchillas de componentes como

{displaystyle A=sum _{J}A_{J}e^{J}.}

Funciones lineales

Aunque un reversor es más fácil de trabajar porque puede ser representado directamente en el álgebra como un multivector, los revisores son un subgrupo de funciones lineales en los multivectores, que todavía se puede utilizar cuando sea necesario. El álgebra geométrica de un $n$ - el espacio vectorial dimensional es abarcado por una base de $2^{n}$ elementos. Si un multivector está representado por un ${displaystyle 2^{n}times 1}$ matriz de columna real de coeficientes de base del álgebra, entonces todas las transformaciones lineales del multivector se pueden expresar como la multiplicación de matriz por una $2^{n}times 2^{n}$ Matriz real. Sin embargo, tal transformación lineal general permite intercambios arbitrarios entre grados, como una "rotación" de un escalar en un vector, que no tiene una interpretación geométrica evidente.

Una transformación lineal general de vectores a vectores es de interés. Con la restricción natural para preservar el álgebra exterior inducida, el morfismo externo de la transformación lineal es la extensión única del reversor. Si $f$ es una función lineal que mapea vectores a vectores, entonces su morfismo externo es la función que obedece a la regla

{displaystyle {underline {mathsf {f}}}(a_{1}wedge a_{2}wedge cdots wedge a_{r})=f(a_{1})wedge f(a_{2})wedge cdots wedge f(a_{r})}

para una cuchilla, extendida a toda el álgebra a través de la linealidad.

Modelado de geometrías

Aunque se ha puesto mucha atención en CGA, se debe tener en cuenta que GA no es solo un álgebra, es parte de una familia de álgebras con la misma estructura esencial.

Modelo de espacio vectorial

${mathcal {G}}(3,0)$ puede ser considerado como una extensión o terminación de álgebra vectorial. De vectores a álgebra geométrica cubre la geometría analítica básica y da una introducción a la proyección estereográfica.

El incluso subalgebra de ${mathcal {G}}(2,0)$ es isomorfo a los números complejos, como se puede ver escribiendo un vector $P$ en términos de sus componentes en una base ortonormal y la izquierda multiplicando por el vector base $e_{1}$ , rendimiento

{displaystyle Z=e_{1}P=e_{1}(xe_{1}+ye_{2})=x(1)+y(e_{1}e_{2}),}

donde nos identificamos ${displaystyle imapsto e_{1}e_{2}}$ desde entonces

{displaystyle (e_{1}e_{2})^{2}=e_{1}e_{2}e_{1}e_{2}=-e_{1}e_{1}e_{2}e_{2}=-1.}

Del mismo modo, el incluso subalgebra de ${mathcal {G}}(3,0)$ con base ${displaystyle {1,e_{2}e_{3},e_{3}e_{1},e_{1}e_{2}}}$ es isomorfo a las quaterniones como se puede ver identificando ${displaystyle imapsto -e_{2}e_{3}}$ , ${displaystyle jmapsto -e_{3}e_{1}}$ y ${displaystyle kmapsto -e_{1}e_{2}}$ .

Cada álgebra asociativa tiene una representación matriz; reemplazar los tres vectores base cartesiana por las matrices Pauli da una representación de ${mathcal {G}}(3,0)$ :

{displaystyle {begin{aligned}e_{1}=sigma _{1}=sigma _{x}&={begin{pmatrix}0&1\1&0end{pmatrix}}\e_{2}=sigma _{2}=sigma _{y}&={begin{pmatrix}0&-i\i&0end{pmatrix}}\e_{3}=sigma _{3}=sigma _{z}&={begin{pmatrix}1&0\0&-1end{pmatrix}},.end{aligned}}}

Puntear el "vector de Pauli" (una diada):

{displaystyle sigma =sigma _{1}e_{1}+sigma _{2}e_{2}+sigma _{3}e_{3}}

con vectores arbitrarios

a

b

y multiplicar a través da:

{displaystyle (sigma cdot a)(sigma cdot b)=acdot b+awedge b}

(Equivalentemente, por inspección,

{displaystyle acdot b+isigma cdot (atimes b)}

)

Modelo de espacio-tiempo

En física, las principales aplicaciones son el álgebra geométrica de Minkowski 3+1 tiempo espacial, ${displaystyle {mathcal {G}}(1,3)}$ , llamado álgebra espacial (STA), o menos comúnmente, ${mathcal {G}}(3,0)$ , interpretó el álgebra del espacio físico (APS).

Mientras que en STA, puntos de tiempo espacial están representados simplemente por vectores, en APS, puntos de ${displaystyle (3+1)}$ - la hora espacial dimensional está representada por paravectores, un vector tridimensional (espacio) más un escalar unidimensional (tiempo).

En el álgebra espacial el tensor de campo electromagnético tiene una representación bivector ${displaystyle {F}=({E}+ic{B})gamma _{0}}$ . Aquí, el ${displaystyle i=gamma _{0}gamma _{1}gamma _{2}gamma _{3}}$ es la unidad pseudoscalar (o elemento de volumen cuatridimensional), $gamma _{0}$ es el vector de unidad en la dirección del tiempo, y $E$ y $B$ son los vectores de campo eléctrico y magnético clásicos (con un componente de tiempo cero). Usando las cuatro corrientes ${J}$ Las ecuaciones de Maxwell se vuelven

Formulación	Ecuaciones homogéneas	Ecuaciones no homogéneas
Campos	$DF=mu _{0}J$
Campos	${displaystyle Dwedge F=0}$	${displaystyle D~rfloor ~F=mu _{0}J}$
Potenciales (cualquier calibre)	$F=Dwedge A$	${displaystyle D~rfloor ~(Dwedge A)=mu _{0}J}$
Potentials (Gauge Lorenz)	$F=DA$ ${displaystyle D~rfloor ~A=0}$	$D^{2}A=mu _{0}J$

En el cálculo geométrico, yuxtaposición de vectores como en $DF$ indicar el producto geométrico y se puede descomponer en partes como ${displaystyle DF=D~rfloor ~F+Dwedge F}$ . Aquí. $D$ es el derivado del covector en cualquier momento espacial y se reduce a $nabla$ en tiempo espacio plano. Donde $bigtriangledown$ juega un papel en Minkowski $4$ -tiempo espacial que es sinónimo del papel de $nabla$ en Euclidean $3$ - espacio y está relacionado con el d'Alembertian por $Box =bigtriangledown ^{2}$ . De hecho, dado un observador representado por un futuro marcando el tiempo vector $gamma _{0}$ tenemos

gamma _{0}cdot bigtriangledown ={frac {1}{c}}{frac {partial }{partial t}}

gamma _{0}wedge bigtriangledown =nabla

Boost en este espacio métrico Lorentziano tiene la misma expresión $e^{beta }$ como rotación en el espacio euclidiano, donde ${beta }$ es el bivector generado por el tiempo y las direcciones espaciales implicadas, mientras que en el caso Euclidean es el bivector generado por las dos direcciones espaciales, fortaleciendo el "analógico" a casi la identidad.

Las matrices Dirac son una representación de ${mathcal {G}}(1,3)$ , mostrando la equivalencia con las representaciones de matriz utilizadas por los físicos.

Modelo homogéneo

Álgebra geométrica proyectiva (PGA), también conocida como el modelo homogéneo, proporciona un álgebra completa que contiene representaciones de todas las isometrías de Euclidean y los subespacios lineales en los que operan. En este modelo se añade una sola dimensión degenerada a la n dimensiones ordinarias del espacio para formar el álgebra ${displaystyle {mathcal {G}}(n,0,1)}$ . Un tratamiento integral ${displaystyle {mathcal {G}}(3,0,1)}$ en particular es dado por Lengyel. En la PGA tridimensional, los vectores corresponden a puntos, los bivectores corresponden a líneas, y los trivectores corresponden a planos. Proper Euclidean isometries, which are always fast motions in 3D space, are represented by motores compuesto por ocho componentes de grado uniforme, e isometrías euclidianas inadecuadas, que contienen una reflexión, están representadas por flectores compuesto por ocho componentes de grado impar. El álgebra motor es la generalización correcta de las dobles quaternions al conjunto completo de objetos que aparecen en PGA.

Un concepto central en PGA es la simetría que surge a través de la inversión de los vectores base que están presentes y ausentes en cada uno de los componentes de un objeto. Esto da lugar no sólo a una dualidad fundamental en los objetos geométricos del álgebra, sino también a las operaciones sobre esos objetos. Cada producto en el álgebra (producto de cuña, producto interior, producto geométrico, producto interior) tiene un "antiproducto" que realiza la misma operación en los duales de sus operandos. La inclusión de ambos tipos de productos es fundamental para completar el álgebra. Las operaciones de unión y encuentro entre varias geometrías se realizan mediante el producto de cuña y su producto dual, el producto anticuña, respectivamente. El producto interno y su dual dan dos normas diferentes, denominadas norma a granel y norma de peso, y éstas producen cantidades escalares y antiescalares, respectivamente. Las isometrías euclidianas son realizadas por el antiproducto geométrico.

Todos los objetos en álgebra geométrica proyectiva son homogéneos, incluidas las magnitudes que serían simplemente escalares en configuraciones no proyectivas. Multiplicar cualquier punto, línea, plano, motor o flector por un escalar distinto de cero no tiene ningún efecto sobre su significado. Un objeto se proyecta en el espacio 3D a través de un proceso llamado unitización, que hace que el tamaño colectivo de los componentes se extienda a la unidad de dimensión degenerada. Las medidas de distancia concretas surgen como magnitudes homogéneas dadas por la norma geométrica, que es una suma de la norma de volumen y la norma de peso. Cuando la norma geométrica se unifica, su componente escalar representa una distancia real.

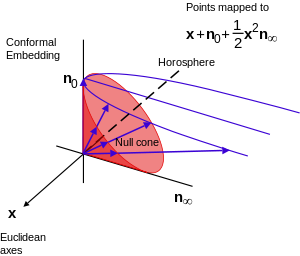
Modelo conforme

Trabajando en el espacio GA, Euclidean ${mathcal {E}}^{3}$ (junto con un punto conformal en la infinidad) está incrustado proyectivamente en el CGA ${displaystyle {mathcal {G}}(4,1)}$ a través de la identificación de puntos de Euclidean con subespacios 1D en el cono null 4D del subespacial vectorial 5D CGA. Esto permite que todas las transformaciones conformales se realicen como rotaciones y reflexiones y es covariante, ampliando las relaciones de incidencia de geometría proyectiva a círculos y esferas.

Específicamente, agregamos vectores de base ortogonal ${displaystyle e_{+}}$ y ${displaystyle e_{-}}$ tales que ${displaystyle e_{+}^{2}=+1}$ y ${displaystyle e_{-}^{2}=-1}$ a la base del espacio vectorial que genera ${mathcal {G}}(3,0)$ e identificar vectores nulos

{displaystyle n_{infty }=e_{-}+e_{+}}

como un punto conformado del infinito (ver Compactificación) y

{displaystyle n_{text{o}}={tfrac {1}{2}}(e_{-}-e_{+})}

como el punto del origen, dando

{displaystyle n_{infty }cdot n_{text{o}}=-1}

Este procedimiento tiene algunas similitudes con el procedimiento para trabajar con coordenadas homogéneas en geometría proyectiva y en este caso permite el modelado de las transformaciones euclidianas de $mathbf{R}^3$ como transformaciones ortogonales de un subconjunto de ${displaystyle mathbf {R} ^{4,1}}$ .

Un área fluida y que cambia rápidamente de GA, CGA también se está investigando para aplicaciones a la física relativista.

Modelos de transformación proyectiva

Actualmente se están investigando dos posibles candidatos como base para la geometría afinal y proyectiva en tres dimensiones ${displaystyle {mathcal {R}}(3,3)}$ y ${displaystyle {mathcal {R}}(4,4)}$ que incluye representaciones para los tijeras y escalar no uniforme, así como superficies cuádricas y secciones cónicas.

Un nuevo modelo de investigación, Álgebra Geométrica Cuádrica Conformal (QCGA) ${displaystyle {mathcal {R}}(9,6)}$ es una extensión de CGA, dedicada a superficies quadric. La idea es representar los objetos en subespacios dimensionales bajos del álgebra. QCGA es capaz de construir superficies cuádricas ya sea usando puntos de control o ecuaciones implícitas. Además, QCGA puede computar la intersección de superficies cuádricas, así como los vectores tangentes superficiales y normales en un punto que se encuentra en la superficie cuádrica.

Interpretación geométrica

Proyección y rechazo

En el espacio 3D, un bivector

aland b

define un subespacio plano 2D (azul claro, se extiende infinitamente en direcciones indicadas). Cualquier vector

c

en el espacio 3D se puede descomponer en su proyección

{displaystyle c_{|}}

sobre un avión y su rechazo

{displaystyle c_{perp }}

de este avión.

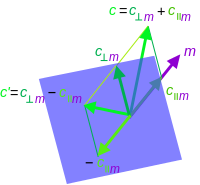
Para cualquier vector $a$ y cualquier vector invertible $m$ ,

{displaystyle a=amm^{-1}=(acdot m+awedge m)m^{-1}=a_{|m}+a_{perp m},}

Donde proyección de $a$ sobre $m$ (o la parte paralela) es

{displaystyle a_{|m}=(acdot m)m^{-1}}

y el rechazo de $a$ desde $m$ (o la parte ortogonal) es

{displaystyle a_{perp m}=a-a_{|m}=(awedge m)m^{-1}.}

Utilizar el concepto de un $k$ -Blade $B$ como representación de un subespacio $V$ y cada multivector que finalmente se expresa en términos de vectores, esto generaliza a proyección de un multivector general sobre cualquier invertible $k$ -Blade $B$ como

{displaystyle {mathcal {P}}_{B}(A)=(A;rfloor ;B^{-1});rfloor ;B,}

con el rechazo definido como

{displaystyle {mathcal {P}}_{B}^{perp }(A)=A-{mathcal {P}}_{B}(A).}

La proyección y el rechazo generalizan a las cuchillas nulas $B$ reemplazando el inverso $B^{-1}$ con el pseudoinverso $B^{{+}}$ con respecto al producto contratante. El resultado de la proyección coincide en ambos casos en cuchillas no nulas. Para cuchillas nulas $B$ , la definición de la proyección dada aquí con la primera contracción en lugar del segundo ser en el pseudoinverso debe ser utilizado, ya que sólo entonces es el resultado necesariamente en el subespacio representado por $B$ . La proyección generaliza a través de la linealidad a los multivectores generales $A$ . La proyección no es lineal en $B$ y no se generaliza a los objetos $B$ que no son espadas.

Reflexión

Los reflejos simples en un hiperplano se expresan fácilmente en el álgebra a través de la conjugación con un solo vector. Estos sirven para generar el conjunto de rotaciones y reflexiones generales del rotor.

Reflexión del vector

c

un vector

m

. Sólo el componente

c

paralelo a

m

se niega.

La reflexión $c'$ de un vector $c$ un vector $m$ , o equivalentemente en la ortogonal hiperplano $m$ , es lo mismo que negar el componente de un vector paralelo a $m$ . El resultado de la reflexión será

{displaystyle c'={-c_{|m}+c_{perp m}}={-(ccdot m)m^{-1}+(cwedge m)m^{-1}}={(-mcdot c-mwedge c)m^{-1}}=-mcm^{-1}}

Esta no es la operación más general que puede considerarse como un reflejo cuando la dimensión ${displaystyle ngeq 4}$ . Una reflexión general puede ser expresada como el compuesto de cualquier número impar de reflexiones de un solo eje. Así, una reflexión general $a'$ de un vector $a$ puede ser escrito

{displaystyle amapsto a'=-MaM^{-1},}

dónde

{displaystyle M=pqcdots r}

{displaystyle M^{-1}=(pqcdots r)^{-1}=r^{-1}cdots q^{-1}p^{-1}.}

Si definimos la reflexión a lo largo de un vector no nulo $m$ del producto de vectores como el reflejo de cada vector en el producto a lo largo del mismo vector, obtenemos para cualquier producto de un número extraño de vectores que, por ejemplo,

(abc)'=a'b'c'=(-mam^{-1})(-mbm^{-1})(-mcm^{-1})=-ma(m^{-1}m)b(m^{-1}m)cm^{-1}=-mabcm^{-1},

y para el producto de un número par de vectores que

{displaystyle (abcd)'=a'b'c'd'=(-mam^{-1})(-mbm^{-1})(-mcm^{-1})(-mdm^{-1})=mabcdm^{-1}.}

Utilizando el concepto de cada multivector que finalmente se expresa en términos de vectores, el reflejo de un multivector general $A$ usando cualquier reversor de reflexión $M$ puede ser escrito

{displaystyle Amapsto Malpha (A)M^{-1},}

Donde $alpha$ es el automorfismo de la reflexión a través del origen del espacio vectorial ( ${displaystyle vmapsto -v}$ ) extendido a través de la linealidad a todo el álgebra.

Rotaciones

Un rotor que gira vectores en un plano gira vectores a través del ángulo

theta

, eso es

{displaystyle xmapsto R_{theta }x{tilde {R}}_{theta }}

es una rotación de

x

a través del ángulo

theta

. El ángulo entre

u

v

theta /2

. Interpretaciones similares son válidas para un multivector general

X

en lugar del vector

x

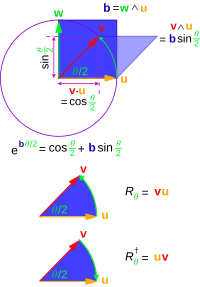
Si tenemos un producto de vectores ${displaystyle R=a_{1}a_{2}cdots a_{r}}$ entonces denotamos el reverso como

{displaystyle {tilde {R}}=a_{r}cdots a_{2}a_{1}.}

Como ejemplo, asuma que $R=ab$ nosotros

{displaystyle R{tilde {R}}=abba=ab^{2}a=a^{2}b^{2}=ba^{2}b=baab={tilde {R}}R.}

Escalada $R$ así ${displaystyle R{tilde {R}}=1}$ entonces

{displaystyle (Rv{tilde {R}})^{2}=Rv^{2}{tilde {R}}=v^{2}R{tilde {R}}=v^{2}}

Así que... ${displaystyle Rv{tilde {R}}}$ deja la longitud $v$ sin cambios. También podemos demostrar que

{displaystyle (Rv_{1}{tilde {R}})cdot (Rv_{2}{tilde {R}})=v_{1}cdot v_{2}}

así como la transformación ${displaystyle Rv{tilde {R}}}$ preserva la longitud y el ángulo. Por lo tanto, puede identificarse como rotación o rotor; $R$ se llama rotor si es una rotación adecuada (como es si se puede expresar como producto de un número uniforme de vectores) y es una instancia de lo que se conoce en GA como un versor.

Hay un método general para rotar un vector que implica la formación de un multivector de la forma ${displaystyle R=e^{-Btheta /2}}$ que produce una rotación $theta$ en el plano y con la orientación definida por $2$ -Blade $B$ .

Los rotores son una generalización de las quaterniones a $n$ - espacios dimensionales.

Versor

A $k$ -versor es un multivector que se puede expresar como el producto geométrico $k$ vectores invertibles. Los quaternions unitarios (originalmente llamados versors por Hamilton) pueden identificarse con rotores en espacio 3D de la misma manera que los verdaderos rotores 2D suman números complejos; para los detalles se refieren a Dorst.

Algunos autores utilizan el término "producto versor" para referirse al caso frecuente en el que un operando está "intercalado" entre operadores. Las descripciones de rotaciones y reflexiones, incluidos sus morfismos externos, son ejemplos de este tipo de intercalado. Estos morfismos externos tienen una forma algebraica particularmente simple. Específicamente, un mapeo de vectores de la forma

{displaystyle Vto V:amapsto RaR^{-1}}

se extiende al morfismo exterior

{displaystyle {mathcal {G}}(V)to {mathcal {G}}(V):Amapsto RAR^{-1}.}

Dado que tanto los operadores como los operandos son versores, existe la posibilidad de ejemplos alternativos, como rotar un rotor o reflejar un espinor, siempre que se pueda asignar algún significado geométrico o físico a tales operaciones.

Por el teorema de Cartan-Dieudonné tenemos que cada isometría se puede dar como reflejos en hiperplanos y dado que los reflejos compuestos proporcionan rotaciones entonces tenemos que las transformaciones ortogonales son versores.

En términos de grupo, para un verdadero, no degenerado ${displaystyle {mathcal {G}}(p,q)}$ , habiendo identificado al grupo ${displaystyle {mathcal {G}}^{times }}$ como el grupo de todos los elementos invertibles ${mathcal {G}}$ , Lundholm da una prueba de que el "grupo de inversores" ${displaystyle {v_{1}v_{2}cdots v_{k}in G:v_{i}in V^{times }}}$ (el conjunto de los versos invertibles) es igual al grupo Lipschitz $Gamma$ ()a.k.a. Grupo Clifford, aunque Lundholm deprecate este uso).

Subgrupos de Γ

Lundholm define el ${displaystyle operatorname {Pin} }$ , ${displaystyle operatorname {Spin} }$ , y ${displaystyle operatorname {Spin} ^{+}}$ subgrupos, generados por vectores de unidad, y en el caso de ${displaystyle operatorname {Spin} }$ y ${displaystyle operatorname {Spin} ^{+}}$ , sólo un número uniforme de tales factores vectoriales pueden estar presentes.

Subgrupo	Definición	Descripción
${displaystyle operatorname {Pin} }$	${displaystyle Xin Gamma:X{tilde {X}}=pm 1}$	unidad
${displaystyle operatorname {Spin} }$	${displaystyle {operatorname {Pin} }cap {mathcal {G}}^{+}}$	incluso revisores de unidad
${displaystyle operatorname {Spin} ^{+}}$	${displaystyle Xin operatorname {Spin}:X{tilde {X}}=1}$	rotores

Los espinores se definen como elementos de la subálgebra par de un AG real; Francis y Kosowsky ofrecen un análisis del enfoque GA de los espinores.

Ejemplos y aplicaciones

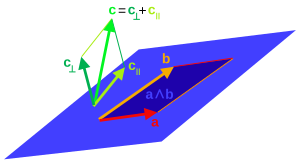
Hipervolumen de un paralelotopo dividido por vectores

Para vectores $a$ y $b$ en un paralelograma que tenemos

awedge b=((awedge b)b^{-1})b=a_{perp b}b

con el resultado de que $awedge b$ es lineal en el producto de la "altitud" y la "base" del paralelograma, es decir, su área.

Interpretaciones similares son verdaderas para cualquier número de vectores que abarcan un $n$ -dimensional paraleótopo; el producto exterior de vectores ${displaystyle a_{1},a_{2},ldotsa_{n}}$ , eso es ${displaystyle textstyle bigwedge _{i=1}^{n}a_{i}}$ , tiene una magnitud igual al volumen del $n$ - Parallelotope. An $n$ -vector no tiene necesariamente una forma de un paraleótopo – esta es una visualización conveniente. Podría ser cualquier forma, aunque el volumen es igual al del paraleótopo.

Intersección de una recta y un plano

Una línea L definida por puntos T y P (que buscamos) y un plano definido por un bivector B que contiene puntos P y Q.

Podemos definir la línea paramétricamente por $p=t+alpha v$ Donde $p$ y $t$ son vectores de posición para los puntos P y T y $v$ es el vector de dirección para la línea.

Entonces

Bwedge (p-q)=0

Bwedge (t+alpha v-q)=0

entonces

alpha ={frac {Bwedge (q-t)}{Bwedge v}}

{displaystyle p=t+left({frac {Bwedge (q-t)}{Bwedge v}}right)v.}

Sistemas rotativos

La descripción matemática de las fuerzas de rotación, como el momento de torsión y el momento angular, a menudo utiliza el producto vectorial del cálculo vectorial en tres dimensiones con una convención de orientación (orientación).

El producto cruzado en relación con el producto exterior. En rojo están el vector normal de la unidad, y el bivector de la unidad "paralela".

El producto vectorial se puede ver en términos del producto exterior, lo que permite una interpretación geométrica más natural del producto vectorial como un bivector utilizando la relación dual

{displaystyle atimes b=-I(awedge b).}

Por ejemplo, el par generalmente se define como la magnitud del componente de fuerza perpendicular por la distancia, o el trabajo por unidad de ángulo.

Suponga un camino circular en un plano arbitrario que contiene vectores ortonormales ${hat {u}}$ y ${hat {v}}$ se parametiza por ángulo.

{displaystyle mathbf {r} =r({hat {u}}cos theta +{hat {v}}sin theta)=r{hat {u}}(cos theta +{hat {u}}{hat {v}}sin theta)}

Al designar el bivector unitario de este plano como el número imaginario

{displaystyle {i}={hat {u}}{hat {v}}={hat {u}}wedge {hat {v}}}

{displaystyle i^{2}=-1}

este vector de ruta se puede escribir convenientemente en forma exponencial compleja

{displaystyle mathbf {r} =r{hat {u}}e^{itheta }}

y la derivada con respecto al ángulo es

{displaystyle {frac {dmathbf {r} }{dtheta }}=r{hat {u}}ie^{itheta }=mathbf {r} i.}

Así que el par, la tasa de cambio de trabajo $W$ , debido a una fuerza $F$ , es

{displaystyle tau ={frac {dW}{dtheta }}=Fcdot {frac {dr}{dtheta }}=Fcdot (mathbf {r} i).}

A diferencia de la descripción del producto de la cruz del par, ${displaystyle tau =mathbf {r} times F}$ , la descripción del álgebra geométrica no introduce un vector en la dirección normal; un vector que no existe en dos y que no es único en más de tres dimensiones. El bivector de unidad describe el plano y la orientación de la rotación, y el sentido de la rotación es relativo al ángulo entre los vectores ${hat {u}}$ y ${hat {v}}$ .

Cálculo geométrico

El cálculo geométrico amplía el formalismo para incluir la diferenciación y la integración, incluidas la geometría diferencial y las formas diferenciales.

Esencialmente, la derivada vectorial se define de modo que la versión GA del teorema de Green sea verdadera,

{displaystyle int _{A}dA,nabla f=oint _{partial A}dx,f}

y luego uno puede escribir

nabla f=nabla cdot f+nabla wedge f

como un producto geométrico, generalizando efectivamente Stokes' teorema (incluida la versión en forma diferencial del mismo).

In $1D$ cuando $A$ es una curva con puntos finales $a$ y $b$ , entonces

{displaystyle int _{A}dA,nabla f=oint _{partial A}dx,f}

reduce a

{displaystyle int _{a}^{b}dx,nabla f=int _{a}^{b}dxcdot nabla f=int _{a}^{b}df=f(b)-f(a)}

o el teorema fundamental del cálculo integral.

También se desarrollan el concepto de variedad vectorial y la teoría de integración geométrica (que generaliza las formas diferenciales).

Historia

Antes del siglo XX

Aunque la conexión de geometría con el álgebra se remonta al menos a Euclides Elementos en el siglo III B.C. (ver álgebra geométrica griega), GA en el sentido utilizado en este artículo no fue desarrollado hasta 1844, cuando fue utilizado en un de manera sistemática para describir las propiedades geométricas y transformaciones de un espacio. En ese año, Hermann Grassmann presentó la idea de un álgebra geométrica en plena generalidad como un determinado cálculo (analógico al cálculo proposicional) que codificaba toda la información geométrica de un espacio. El sistema algebraico de Grassmann podría ser aplicado a varios tipos de espacios diferentes, el jefe entre ellos es el espacio euclidiano, el espacio afinado y el espacio proyector. Después de Grassmann, en 1878 William Kingdon Clifford examinó el sistema algebraico de Grassmann junto a las quaternions de William Rowan Hamilton en (Clifford 1878) harv error: no target: CITEREFClifford1878 (help). Desde su punto de vista, las quaterniones describen ciertas transformaciones (que llamó rotores), mientras que el álgebra de Grassmann describió cierta propiedades (o Strecken como longitud, área y volumen). Su contribución era definir un nuevo producto — el producto geométrico– en un álgebra Grassmann existente, que realizó las cuaterniones como vivir dentro de ese álgebra. Posteriormente, Rudolf Lipschitz en 1886 generalizó la interpretación de Clifford de los quaternions y los aplicó a la geometría de las rotaciones en $n$ dimensiones. Más tarde estos desarrollos llevarían a otros matemáticos del siglo XX a formalizar y explorar las propiedades del álgebra Clifford.

Sin embargo, otro desarrollo revolucionario del siglo XIX eclipsaría por completo las álgebras geométricas: el análisis vectorial, desarrollado de forma independiente por Josiah Willard Gibbs y Oliver Heaviside. El análisis vectorial fue motivado por los estudios de electromagnetismo de James Clerk Maxwell, y específicamente por la necesidad de expresar y manipular convenientemente ciertas ecuaciones diferenciales. El análisis vectorial tenía cierto atractivo intuitivo en comparación con los rigores de las nuevas álgebras. Físicos y matemáticos por igual lo adoptaron rápidamente como su conjunto de herramientas geométricas de elección, particularmente siguiendo el influyente libro de texto de 1901 Análisis vectorial de Edwin Bidwell Wilson, siguiendo las conferencias de Gibbs.

En más detalle, han habido tres enfoques de álgebra geométrica: análisis cuaternónico, iniciado por Hamilton en 1843 y geometrizado como rotores por Clifford en 1878; álgebra geométrica, iniciada por Grassmann en 1844; y análisis vectorial, desarrollado a finales del siglo XIX por Gibbs y Heaviside. El legado del análisis cuaternónico en el análisis vectorial se puede ver en el uso de $i$ , $j$ , $k$ para indicar los vectores de base de $mathbf{R}^3$ : está siendo pensado como las quaterniones puramente imaginarias. Desde la perspectiva del álgebra geométrica, el incluso subalgebra del tiempo espacial Álgebra es isomorfo a la GA del espacio euclidiano 3D y las quaterniones son isomorfos al subalgebra incluso de la GA del espacio euclidiano 3D, que unifica los tres enfoques.

Siglo XX y presente

El progreso en el estudio de las álgebras de Clifford avanzó silenciosamente durante el siglo XX, aunque en gran parte se debió al trabajo de algebristas abstractos como Élie Cartan, Hermann Weyl y Claude Chevalley. El enfoque geométrico de las álgebras geométricas ha tenido varios renacimientos en el siglo XX. En matemáticas, el Álgebra geométrica de Emil Artin analiza el álgebra asociada con cada una de varias geometrías, incluida la geometría afín, la geometría proyectiva, la geometría simpléctica y la geometría ortogonal. En física, las álgebras geométricas han sido revividas como un "nuevo" forma de hacer mecánica clásica y electromagnetismo, junto con temas más avanzados como la mecánica cuántica y la teoría de calibre. David Hestenes reinterpretó las matrices de Pauli y Dirac como vectores en el espacio y el espacio-tiempo ordinarios, respectivamente, y ha sido uno de los principales defensores contemporáneos del uso del álgebra geométrica.

En gráficos por computadora y robótica, se han revivido las álgebras geométricas para representar eficientemente las rotaciones y otras transformaciones. Para aplicaciones de GA en robótica (teoría de tornillos, cinemática y dinámica usando versores), visión artificial, control y computación neuronal (aprendizaje geométrico) ver Bayro (2010).

Referencias y lecturas adicionales

Arreglado cronológicamente

Contenido relacionado

Más resultados...