Álgebra exterior
En matemáticas, la álgebra exterior, o Álgebra Grassmann, nombrado por Hermann Grassmann, es un álgebra que utiliza el producto exterior o producto de cuña como su multiplicación. En matemáticas, la producto exterior o producto de cuña de vectores es una construcción algebraica utilizada en geometría para estudiar áreas, volúmenes, y sus análogos de mayor dimensión. El producto exterior de dos vectores u{displaystyle u} yv,{displaystyle v,} denotado por u∧ ∧ v,{displaystyle uwedge v,} se llama bivector y vive en un espacio llamado el exterior, un espacio vectorial que es distinto del espacio original de vectores. La magnitud de la u∧ ∧ v{displaystyle uwedge v} se puede interpretar como el área del paralelograma con los lados u{displaystyle u} yv,{displaystyle v,} que en tres dimensiones también se puede calcular utilizando el producto cruzado de los dos vectores. Más generalmente, todas las superficies planas paralelas con la misma orientación y área tienen el mismo bivector como una medida de su área orientada. Como el producto cruzado, el producto exterior es anticommutante, lo que significa que u∧ ∧ v=− − ()v∧ ∧ u){displaystyle uwedge v=-(vwedge u)} para todos los vectores u{displaystyle u} yv,{displaystyle v,} pero, a diferencia del producto cruzado, el producto exterior es asociativo.
Cuando se considera de esta manera, el producto exterior de dos vectores se denomina 2 palas. De manera más general, el producto exterior de cualquier número k de vectores se puede definir y, en ocasiones, se denomina cuchilla k. Vive en un espacio conocido como el k-ésimo poder exterior. La magnitud de la hoja k resultante es el hipervolumen orientado del paralelotopo dimensional k cuyos bordes son los vectores dados, al igual que la magnitud del triple producto escalar de vectores en tres dimensiones da el volumen del paralelepípedo generado por esos vectores.
El álgebra exterior proporciona un entorno algebraico en el que responder preguntas geométricas. Por ejemplo, las cuchillas tienen una interpretación geométrica concreta, y los objetos en el álgebra exterior pueden ser manipulados según un conjunto de reglas inequívocas. El álgebra exterior contiene objetos que no son sólo k-Blades, pero sumas de k-Blades; tal suma se llama un k-vector. El k-negros, porque son productos simples de vectores, se llaman los elementos simples del álgebra. El rango de cualquiera k- el vencedor se define como el menor número de elementos simples de los cuales es una suma. El producto exterior se extiende al álgebra exterior completa, por lo que tiene sentido multiplicar los dos elementos del álgebra. Equipado con este producto, el álgebra exterior es un álgebra asociativa, lo que significa que α α ∧ ∧ ()β β ∧ ∧ γ γ )=()α α ∧ ∧ β β )∧ ∧ γ γ {displaystyle alpha wedge (beta wedge gamma)=(alpha wedge beta)wedge gamma } para cualquier elemento α α ,β β ,γ γ .{displaystyle alphabetagamma.} El k- Los ganadores tienen título k, lo que significa que son sumas de productos de k vectores. Cuando los elementos de diferentes grados se multiplican, los grados agregan como multiplicación de polinomios. Esto significa que el álgebra exterior es un álgebra de grado.
La definición del álgebra exterior tiene sentido para espacios no solo de vectores geométricos, sino también de otros objetos similares a vectores, como campos vectoriales o funciones. En general, el álgebra exterior se puede definir para módulos sobre un anillo conmutativo y para otras estructuras de interés en álgebra abstracta. Es una de estas construcciones más generales donde el álgebra exterior encuentra una de sus aplicaciones más importantes, donde aparece como el álgebra de formas diferenciales que es fundamental en áreas que utilizan la geometría diferencial. El álgebra exterior también tiene muchas propiedades algebraicas que lo convierten en una herramienta conveniente en el álgebra misma. La asociación del álgebra exterior a un espacio vectorial es un tipo de funtor sobre espacios vectoriales, lo que significa que es compatible en cierto modo con transformaciones lineales de espacios vectoriales. El álgebra exterior es un ejemplo de biálgebra, lo que significa que su espacio dual también posee un producto, y este producto dual es compatible con el producto exterior. Esta álgebra dual es precisamente el álgebra de formas multilineales alternas, y el apareamiento entre el álgebra exterior y su dual viene dado por el producto interior.
Ejemplos motivadores
Los primeros dos ejemplos asumen un campo tensor métrico y una orientación; el tercer ejemplo tampoco asume.
Áreas en el plano
El avión cartesiano R2{displaystyle mathbb {R} {2}} es un espacio vectorial real equipado con una base que consiste en un par de vectores de unidad
- e1=[10],e2=[01],{displaystyle {Mathbf} }_{1}={begin{bmatrix}1end{bmatrix}quad {fnMitbf} }_{2}={begin{bmatrix}01end{bmatrix}} con la orientación e1× × e2{displaystyle mathbf {e} _{1}times mathbf {e} ¿Qué? y con la métrica [1001].{displaystyle {begin{bmatrix}1 {}}}}}
Supongamos que
- v=[ab]=ae1+be2,w=[cd]=ce1+de2{begin{bmatrix}}=amathbf} {c} {c} {cc}=amathbf {c} {c}cc}ccccccc}ccccccccH00} ¿Qué?
son un par de vectores dados en R2,{displaystyle mathbb {R} ^{2} escrito en componentes. Hay un paralelograma único que tiene v y w como dos de sus lados. El zona de este paralelogramo se da por la fórmula determinante estándar:
- Zona=SilencioDet[vw]Silencio=SilencioDet[acbd]Silencio=Silencioad− − bcSilencio.{displaystyle {text{Area}={ Bigl }det {begin{bmatrix}mathbf {v} &mathbf {w}end{bmatrix}}{ Más grande que nunca. Biggr tención}=left WordPressad-bcright sobre la vida.}
Considere ahora el producto exterior de v y w:
- v∧ ∧ w=()ae1+be2)∧ ∧ ()ce1+de2)=ace1∧ ∧ e1+ade1∧ ∧ e2+bce2∧ ∧ e1+bde2∧ ∧ e2=()ad− − bc)e1∧ ∧ e2{displaystyle {begin{aligned}mathbf {v} wedge mathbf {w}=(amathbf {e} _{1}+bmathbf {e} {2})Suecia (cmathbf {e} _{1}+dmathbf {e} _{2})\ {=acmathbf {e} _{1}Suecia mathbf {e} _{1}+admathbf {e} _{1}}e}demathbf {e} ¿Por qué? ¿Por qué?
donde el primer paso utiliza la ley distributiva para el producto exterior, y el último utiliza el hecho de que el producto exterior se alterna, y en particular e2∧ ∧ e1=− − ()e1∧ ∧ e2).{displaystyle mathbf {e} _{2}wedge mathbf {e} _{1}=-(mathbf {e} _{1}wedge mathbf {e} _{2}). } (El hecho de que el producto exterior se alterna también fuerza e1∧ ∧ e1=e2∧ ∧ e2=0.{displaystyle mathbf {e} _{1}wedge mathbf {e} ¿Por qué?) Tenga en cuenta que el coeficiente en esta última expresión es precisamente el determinante de la matriz [v w]. El hecho de que esto pueda ser positivo o negativo tiene el significado intuitivo de que v y w puede estar orientado en un sentido contrario a la aguja del reloj como los vértices del paralelograma que definen. Tal área se llama el Área firmada del paralelograma: el valor absoluto del área firmada es el área ordinaria, y el signo determina su orientación.
El hecho de que este coeficiente sea el área firmada no es un accidente. De hecho, es relativamente fácil ver que el producto exterior debe estar relacionado con el área firmada si se trata de axiomatizar esta área como una construcción algebraica. En detalle, si A(v, w) denota el área firmada del paralelogramo del cual el par de vectores v y w forman dos lados adyacentes, entonces A debe satisfacer las siguientes propiedades:
- A(rv, sw) rsA(v, w) para cualquier número real r y s, ya que el rescalamiento de cualquiera de las partes reescala la zona por la misma cantidad (y la inversión de la dirección de uno de los lados revierte la orientación del paralelograma).
- A(v, v) = 0, desde el área del paralelograma degenerado determinado por v (es decir, un segmento de línea) es cero.
- A(w, v−Av, w), desde el intercambio de roles v y w revierte la orientación del paralelograma.
- A(v + rw, w.v, w) para cualquier número real r, desde la adición de un múltiple de w a v no afecta a la base ni a la altura del paralelograma y, por consiguiente, preserva su área.
- A(e1, e2) = 1, ya que el área de la plaza unidad es uno.
Con la excepción de la última propiedad, el producto exterior de dos vectores satisface las mismas propiedades que el área. En cierto sentido, el producto exterior generaliza la propiedad final al permitir comparar el área de un paralelogramo con la de cualquier paralelogramo elegido en un plano paralelo (aquí, el que tiene lados e 1 y e2). En otras palabras, el producto exterior proporciona una formulación de área independiente de la base.
Productos cruzados y triples
Para vectores en un espacio vectorial tridimensional orientado con un producto escalar bilineal, el álgebra exterior está estrechamente relacionada con el producto vectorial y el producto triple. Usando una base estándar (e1, e2, e3), el producto exterior de un par de vectores
- u=u1e1+u2e2+u3e3{displaystyle mathbf {u} =u_{1}mathbf {e} ¿Qué? ¿Qué? ¿Qué?
y
- v=v1e1+v2e2+v3e3{displaystyle mathbf {v} =v_{1}mathbf {e} ¿Por qué? ¿Qué?
es
- u∧ ∧ v=()u1v2− − u2v1)()e1∧ ∧ e2)+()u2v3− − u3v2)()e2∧ ∧ e3)+()u3v1− − u1v3)()e3∧ ∧ e1),{cH00} {cH00} {cH00} {cH00} {cH00} {ccH00} {ccH00}} {cH00} {cH00} {cH00} {cH00}} {cH00}} {ccH00}
Donde ()e1 ∧ e2, e2 ∧ e3, e3 ∧ e1) es una base para el espacio tridimensional ⋀ ⋀ 2()R3).{textstyle bigwedge nolimits ^{2}left(mathbb {R} ^{3}right). } Los coeficientes anteriores son los mismos que los de la definición habitual del producto cruzado de vectores en tres dimensiones con una orientación dada, las únicas diferencias siendo que el producto exterior no es un vector ordinario, sino que es un 2-vector, y que el producto exterior no depende de la elección de orientación.
Traer un tercer vector
- w=w1e1+w2e2+w3e3,{displaystyle mathbf {w} ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ♪ ¿Qué? ¿Qué?
el producto exterior de tres vectores es
- u∧ ∧ v∧ ∧ w=()u1v2w3+u2v3w1+u3v1w2− − u1v3w2− − u2v1w3− − u3v2w1)()e1∧ ∧ e2∧ ∧ e3){displaystyle mathbf {u} wedge mathbf {v} wedge mathbf {w} {f} {f}* _{3}}
Donde e1 ∧ e2 ∧ e3 es el vector base para el espacio unidimensional ⋀ ⋀ 3()R3).{textstyle bigwedge nolimits ^{3}left(mathbb {R} ^{3}right). } El coeficiente de escalar es el triple producto de los tres vectores.
El producto vectorial y el producto triple en un espacio vectorial euclidiano tridimensional admiten interpretaciones tanto geométricas como algebraicas, a través de la dualidad de la estrella de Hodge. El producto vectorial u × v se puede interpretar como un vector que es perpendicular a ambos u y v y cuya magnitud es igual al área del paralelogramo determinada por los dos vectores. También se puede interpretar como el vector formado por los menores de la matriz con columnas u y v. El producto triple de u, v y w es un escalar con signo que representa un volumen con orientación geométrica. Algebraicamente, es el determinante de la matriz con las columnas u, v y w. El producto exterior en tres dimensiones admite interpretaciones similares: también puede identificarse con líneas orientadas, áreas, volúmenes, etc., que están atravesados por uno, dos o más vectores. El producto exterior generaliza estas nociones geométricas a todos los espacios vectoriales ya cualquier número de dimensiones, incluso en ausencia de un producto escalar.
Campo electromagnético
En las teorías de la relatividad de Einstein, el campo electromagnético generalmente se da como una forma diferencial 2 F=dA{displaystyle F=dA} en 4-espacio o como el campo de tensión alternante equivalente Fij=A[i,j]=A[i;j],{displaystyle F_{ij}=A_{[i,j]}=A_{[i;j]} el tensor electromagnético. Entonces... dF=ddA=0{displaystyle dF=ddA=0} o la identidad equivalente de Bianchi F[ij,k]=F[ij;k]=0.{displaystyle F_{[ij,k]}=F_{[ij;k]}=0.}Nada de esto requiere una métrica.
Añadiendo la métrica de Lorentz y una orientación proporciona el operador estrella Hodge ⋆ ⋆ {displaystyle star } y por lo tanto hace posible definir J=⋆ ⋆ d⋆ ⋆ F{displaystyle J={star }d{star }F} o la divergencia del tensor equivalente Ji=F,jij=F;jij{displaystyle ¿Qué? Donde Fij=gikgjlFkl.{displaystyle F^{ij}=g^{ik}g^{jl}F_{kl}
Definiciones formales y propiedades algebraicas
El álgebra exterior ⋀ ⋀ ()V){textstyle bigwedge (V)} de un espacio vectorial V sobre un terreno K se define como el álgebra cociente del álgebra tensor T()V) por el ideal de dos caras I generado por todos los elementos de la forma x ⊗ x para x ▪ V (es decir, todos los tensores que se pueden expresar como el producto tensor de un vector en V por sí mismo). El ideal I contiene el ideal J generados por elementos de la forma x⊗ ⊗ Sí.+Sí.⊗ ⊗ x=()x+Sí.)⊗ ⊗ ()x+Sí.)− − x⊗ ⊗ x− − Sí.⊗ ⊗ Sí.{displaystyle xotimes y+yotimes x=(x+y)otimes (x+y)-xotimes x-yotimes y} y estos ideales coinciden si char ()K)ل ل 2{displaystyle operatorname {char} (K)neq 2} (si char ()K)=2,{displaystyle operatorname {char}=2,} estos ideales son diferentes excepto el espacio vectorial cero.
Entonces,
- ⋀ ⋀ ()V)=T()V)/I{displaystyle {textstyle bigwedge }(V)=T(V)/I}
es un álgebra asociativa. Su multiplicación se llama producto exterior, y denotado ∧. Esto significa que el producto de ⋀ ⋀ ()V){textstyle bigwedge (V)} es inducido por el producto tensor ⊗ de T()V).
As T0 = K, T1 = V, y ()T0()V)⊕ ⊕ T1()V))∩ ∩ I={}0},{displaystyle left(T^{0}(V)oplus T^{1}(V)right)cap I={0} las inclusiones de K y V dentro T()V) inducir inyecciones de K y V en ⋀ ⋀ ()V).{textstyle bigwedge (V).} Estas inyecciones son comúnmente consideradas como inclusiones, y llamadas incrustaciones naturales, inyecciones naturales o inclusiones naturales. La palabra canónica también se utiliza comúnmente en lugar de naturales naturales.
Producto alternativo
El producto exterior es por construcción alternando en elementos V,{displaystyle V,} que significa que x∧ ∧ x=0{textstyle xwedge x=0} para todos x▪ ▪ V,{displaystyle xin V,} por la construcción anterior. De ahí que el producto también sea anticommutante sobre elementos V,{displaystyle V,} para suponer eso x,Sí.▪ ▪ V,{displaystyle x,yin V,}
- 0=()x+Sí.)∧ ∧ ()x+Sí.)=x∧ ∧ x+x∧ ∧ Sí.+Sí.∧ ∧ x+Sí.∧ ∧ Sí.=x∧ ∧ Sí.+Sí.∧ ∧ x{displaystyle 0=(x+y)wedge (x+y)=xwedge x+xwedge y+ywedge x+ywedge y=xwedge y+ywedge x}
por lo tanto
- x∧ ∧ Sí.=− − ()Sí.∧ ∧ x).{displaystyle xwedge y=-(ywedge x).}
Más generalmente, si σ es una permutación de los números enteros [1,..., k], y x1, x2,..., x k son elementos de V, se sigue que
- xσ σ ()1)∧ ∧ xσ σ ()2)∧ ∧ ⋯ ⋯ ∧ ∧ xσ σ ()k)=Sgn ()σ σ )x1∧ ∧ x2∧ ∧ ⋯ ⋯ ∧ ∧ xk,{displaystyle x_{sigma (1)}wedge x_{sigma (2)}wedge cdots wedge x_{sigma (k)}=operatorname {sgn} (sigma)x_{1}wedge x_{2}wedge cdots wedge x_{k}}
donde sgn(σ) es la firma de la permutación σ.
En particular, si xi = xj para algunos i ≠ j, entonces también se cumple la siguiente generalización de la propiedad de alternancia:
- x1∧ ∧ x2∧ ∧ ⋯ ⋯ ∧ ∧ xk=0.{displaystyle x_{1}wedge x_{2}wedge cdots wedge x_{k}=0.}
Junto con la propiedad distributiva del producto exterior, otra generalización es que si y sólo si {}x1,x2,⋯ ⋯ ,xk}{displaystyle {x_{1},x_{2},cdotsx_{k}} es un conjunto linealmente dependiente de vectores, entonces
- x1∧ ∧ x2∧ ∧ ⋯ ⋯ ∧ ∧ xk=0.{displaystyle x_{1}wedge x_{2}wedge cdots wedge x_{k}=0.}
Energía exterior
El kT potencia exterior de V, denotado ⋀ ⋀ k()V),{textstyle bigwedge nolimits ^{k}(V),} es el subespacio vectorial ⋀ ⋀ ()V){textstyle bigwedge (V)} abarcado por elementos de la forma
- x1∧ ∧ x2∧ ∧ ⋯ ⋯ ∧ ∧ xk,xi▪ ▪ V,i=1,2,...... ,k.{displaystyle x_{1}wedge x_{2}wedge cdots wedge x_{k},quad x_{i}in V,i=1,2,ldotsk.}
Si α α ▪ ▪ ⋀ ⋀ k()V),{textstyle alpha in bigwedge nolimits ^{k}(V),} entonces α se dice que es un k-vector. Si, además, α se puede expresar como un producto exterior k elementos V, entonces α se dice que descompuesto. Aunque descompuesto k- lapso de vencedores ⋀ ⋀ k()V),{textstyle bigwedge nolimits ^{k}(V),} no todos los elementos ⋀ ⋀ k()V){textstyle bigwedge nolimits ^{k}(V)} es descompuesto. Por ejemplo, en R4,{displaystyle mathbb {R} {4}} el siguiente 2-vector no es descompuesto:
- α α =e1∧ ∧ e2+e3∧ ∧ e4.{displaystyle alpha =e_{1}wedge E_{2}+e_{3}wedge E_{4}.
(Esta es una forma simpléctica, ya que α ∧ α ≠ 0).
Base y dimensión
Si la dimensión de V es n y { e1, …, en } es una base para V, entonces el conjunto
- <math alttext="{displaystyle {,e_{i_{1}}wedge e_{i_{2}}wedge cdots wedge e_{i_{k}}~{big |}~~1leq i_{1}<i_{2}<cdots {}ei1∧ ∧ ei2∧ ∧ ⋯ ⋯ ∧ ∧ eikSilencio1≤ ≤ i1.i2.⋯ ⋯ .ik≤ ≤ n}{displaystyle {fnMicrosoft Sans Serif} e_{i_{2}wedge cdots wedge ¿Qué?<img alt="{displaystyle {,e_{i_{1}}wedge e_{i_{2}}wedge cdots wedge e_{i_{k}}~{big |}~~1leq i_{1}<i_{2}<cdots
es una base para ⋀ ⋀ k()V).{textstyle bigwedge nolimits ^{k}(V).} La razón es la siguiente: dada cualquier producto exterior de la forma
- v1∧ ∧ ⋯ ⋯ ∧ ∧ vk,{displaystyle v_{1}wedge cdots wedge v_{k}
cada vector vj se puede escribir como una combinación lineal de los vectores base ei; usando la bilinealidad del producto exterior, esto se puede expandir a una combinación lineal de productos exteriores de esos vectores base. Cualquier producto exterior en el que el mismo vector base aparezca más de una vez es cero; cualquier producto exterior en el que los vectores base no aparezcan en el orden correcto puede reordenarse, cambiando de signo cada vez que dos vectores base cambien de lugar. En general, los coeficientes resultantes de los k-vectores base se pueden calcular como los menores de la matriz que describe los vectores vj en términos de la base ei.
Contando los elementos de base, la dimensión de ⋀ ⋀ k()V){textstyle bigwedge nolimits ^{k}(V)} es igual a un coeficiente binomial:
- dim ⋀ ⋀ k()V)=()nk).{displaystyle dim {textstyle bigwedge }^{k}(V)={binom {fn},}
Donde n es la dimensión de la vectores, y k es el número de vectores en el producto. El coeficiente binomial produce el resultado correcto, incluso para casos excepcionales; en particular, ⋀ ⋀ k()V)={}0}{textstyle bigwedge nolimits ^{k}(V)={0} para k ■ n.
Cualquier elemento del álgebra exterior se puede escribir como una suma de k-vectores. Por lo tanto, como espacio vectorial, el álgebra exterior es una suma directa
- ⋀ ⋀ ()V)=⋀ ⋀ 0()V)⊕ ⊕ ⋀ ⋀ 1()V)⊕ ⊕ ⋀ ⋀ 2()V)⊕ ⊕ ⋯ ⋯ ⊕ ⊕ ⋀ ⋀ n()V){displaystyle {textstyle bigwedge }(V)={textstyle bigwedge }^{0}(V)oplus {textstyle bigwedge }{1}(V)oplus {textstylebigwedge }{2}(V)oplus cdots {oplus {textstylebigwed
(donde por convención ⋀ ⋀ 0()V)=K,{textstyle bigwedge nolimits ^{0}(V)=K,} sobre el terreno V, y ⋀ ⋀ 1()V)=V{textstyle bigwedge nolimits ^{1}(V)=V}), y por lo tanto su dimensión es igual a la suma de los coeficientes binomiales, que es 2n.
Rango de un vector k
Si α α ▪ ▪ ⋀ ⋀ k()V),{textstyle alpha in bigwedge nolimits ^{k}(V),} entonces es posible expresar α como una combinación lineal de k-vectores descompuestos:
- α α =α α ()1)+α α ()2)+⋯ ⋯ +α α ()s){displaystyle alpha =alpha ^{(1)}+alpha ^{(2)}+cdots +alpha ^{(s)}
donde cada α(i) es descomponible, digamos
- α α ()i)=α α 1()i)∧ ∧ ⋯ ⋯ ∧ ∧ α α k()i),i=1,2,...... ,s.{displaystyle alpha ^{(i)}=alpha _{1}{(i)}wedge cdots wedge alpha _{k}^{(i)},quad i=1,2,ldotss.}
El rango del vector k α es el número mínimo de vectores k descomponibles en tales una expansión de α. Esto es similar a la noción de rango tensorial.
El rango es particularmente importante en el estudio de 2 vectores (Sternberg 1964, §III.6) (Bryant et al. 1991). El rango de un α de 2 vectores se puede identificar con la mitad del rango de la matriz de coeficientes de α en una base. Por lo tanto, si ei es una base para V, entonces α se puede expresar únicamente como
- α α =.. i,jaijei∧ ∧ ej{displaystyle alpha =sum {fnMicrosoft Sans Serif} E_{j}
donde aij = −aji (la matriz de coeficientes es sesgadamente simétrica). El rango de la matriz aij es por lo tanto par, y es el doble del rango de la forma α.
En la característica 0, el 2-vector α tiene rango p si y solo si
- α α ∧ ∧ ⋯ ⋯ ∧ ∧ α α ⏟ ⏟ pل ل 0{displaystyle {compset {compsets} {alpha wedge cdots wedge alpha }}neq 0 } y α α ∧ ∧ ⋯ ⋯ ∧ ∧ α α ⏟ ⏟ p+1=0.{displaystyle {underset {p+1}{underbrace {alpha wedge cdots wedge alpha } }=0.}
Estructura graduada
El producto exterior de un vector k con un vector p es un (k + p)-vector, invocando una vez más la bilinealidad. En consecuencia, la descomposición en suma directa del apartado anterior
- ⋀ ⋀ ()V)=⋀ ⋀ 0()V)⊕ ⊕ ⋀ ⋀ 1()V)⊕ ⊕ ⋀ ⋀ 2()V)⊕ ⊕ ⋯ ⋯ ⊕ ⊕ ⋀ ⋀ n()V){displaystyle {textstyle bigwedge }(V)={textstyle bigwedge }^{!0}(V)oplus {textstyle bigwedge }^{!1}(V)oplus {gtextstyle bigwedge }^{2}(V)oplus cdotsoplus {oplus {g}
le da al álgebra exterior la estructura adicional de un álgebra graduada, es decir
- ⋀ ⋀ k()V)∧ ∧ ⋀ ⋀ p()V)⊂ ⊂ ⋀ ⋀ k+p()V).{displaystyle {textstyle bigwedge }^{k}(V)wedge {textstyle bigwedge }^{p}(V)subset {textstyle bigwedge }^{k+p}(V).}
Además, si K es el campo base, tenemos
- ⋀ ⋀ 0()V)=K{displaystyle {textstyle bigwedge }{}(V)=K} y ⋀ ⋀ 1()V)=V.{displaystyle {textstyle bigwedge }{!1}(V)=V.}
El producto exterior es anticommutante de grado, lo que significa que si α α ▪ ▪ ⋀ ⋀ k()V){textstyle alpha in bigwedge nolimits ^{k}(V)} y β β ▪ ▪ ⋀ ⋀ p()V),{textstyle beta in bigwedge nolimits ^{p}(V),} entonces
- α α ∧ ∧ β β =()− − 1)kpβ β ∧ ∧ α α .{displaystyle alpha wedge beta =(-1)^{kp}beta wedge alpha.}
Además de estudiar la estructura graduada en el álgebra exterior, Bourbaki (1989) estudia estructuras graduadas adicionales en el álgebra exterior, como las del álgebra exterior de un módulo graduado (un módulo que ya lleva su propia gradación).
Propiedad universal
Vamos V ser un espacio vectorial sobre el terreno K. Informalmente, multiplicación en ⋀ ⋀ ()V){textstyle bigwedge (V)} se realiza manipulando símbolos e imponiendo una ley distributiva, una ley asociativa y utilizando la identidad v∧ ∧ v=0{displaystyle vwedge v=0} para v ▪ V. Formalmente, ⋀ ⋀ ()V){textstyle bigwedge (V)} es el álgebra "más general" en el que estas reglas sostienen para la multiplicación, en el sentido de que cualquier asociación unitaria K- álgebra que contiene V con multiplicación alternada en V debe contener una imagen homomórfica ⋀ ⋀ ()V).{textstyle bigwedge (V).} En otras palabras, el álgebra exterior tiene la siguiente propiedad universal:
Dado cualquier asociación unitaria K- álgebra A y cualquier K- mapa lineal j:V→ → A{displaystyle j:Vto A} tales que j()v)j()v)=0{displaystyle j(v)j(v)=0} para todos v dentro V, entonces existe Precisamente uno homomorfismo de álgebra unitaria f:⋀ ⋀ ()V)→ → A{textstyle f:bigwedge (V)to A} tales que j()v) f()i()v) para todos v dentro V (Aquí) i es la inclusión natural de V dentro ⋀ ⋀ ()V),{textstyle bigwedge (V),} véase supra).
Para construir el álgebra más general que contiene V y cuya multiplicación se alterna V, es natural comenzar con el álgebra asociativa más general que contiene V, el álgebra tensor T()V), y luego hacer cumplir la propiedad alternando tomando un cociente adecuado. Tomamos el ideal de dos caras I dentro T()V) generado por todos los elementos de la forma v ⊗ v para v dentro V, y definir ⋀ ⋀ ()V){textstyle bigwedge (V)} como el cociente
- ⋀ ⋀ ()V)=T()V)/I{displaystyle {textstyle bigwedge }(V)=T(V)/I }
(y uso ∧ como el símbolo para la multiplicación en ⋀ ⋀ ()V){textstyle bigwedge (V)}). Entonces es sencillo mostrar que ⋀ ⋀ ()V){textstyle bigwedge (V)} contiene V y satisface la propiedad universal anterior.
Como consecuencia de esta construcción, el funcionamiento de la asignación a un espacio vectorial V su álgebra exterior ⋀ ⋀ ()V){textstyle bigwedge (V)} es un functor de la categoría de espacios vectoriales a la categoría de álgebras.
En lugar de definir ⋀ ⋀ ()V){textstyle bigwedge (V)} primero y luego identificar los poderes exteriores ⋀ ⋀ k()V){textstyle bigwedge nolimits ^{k}(V)} como ciertos subespacios, se puede definir alternativamente los espacios ⋀ ⋀ k()V){textstyle bigwedge nolimits ^{k}(V)} primero y luego combinarlos para formar el álgebra ⋀ ⋀ ()V).{textstyle bigwedge (V).} Este enfoque se utiliza a menudo en geometría diferencial y se describe en la siguiente sección.
Generalizaciones
Dado un anillo conmutativo R y un R- Mobiliario M, podemos definir el álgebra exterior ⋀ ⋀ ()M){textstyle bigwedge (M)} como arriba, como un cociente adecuado del álgebra tensor T()M). Sacará la propiedad universal analógica. Muchas de las propiedades ⋀ ⋀ ()M){textstyle bigwedge (M)} también requieren que M ser un módulo de proyecto. Cuando se utiliza la dimensionalidad finita, las propiedades requieren además que M ser finitamente generado y proyectivo. Las generalizaciones a las situaciones más comunes se pueden encontrar en Bourbaki (1989).
Las álgebras exteriores de paquetes vectoriales se consideran con frecuencia en geometría y topología. No existen diferencias esenciales entre las propiedades algebraicas del álgebra exterior de paquetes vectoriales de dimensión finita y las del álgebra exterior de módulos proyectivos finitamente generados, por el teorema de Serre-Swan. Se pueden definir álgebras exteriores más generales para haces de módulos.
Álgebra tensorial alterna
Si K es un campo de característica 0, entonces el álgebra exterior de un espacio vectorial V sobre K se puede identificar canónicamente con el subespacio vectorial de T(V) formado por tensores antisimétricos. Recuerda que el álgebra exterior es el cociente de T(V) por el ideal I generado por elementos de la forma x ⊗ x.
Sea Tr(V) el espacio de tensores homogéneos de grado r. Esto es atravesado por tensores descomponibles
- v1⊗ ⊗ ⋯ ⋯ ⊗ ⊗ vr,vi▪ ▪ V.{displaystyle v_{1}otimes cdots otimes v_{r},quad v_{i}in V.}
La antisimetrización (o, a veces, la simetrización sesgada) de un tensor descomponible se define mediante
- Alt ()v1⊗ ⊗ ⋯ ⋯ ⊗ ⊗ vr)=1r!.. σ σ ▪ ▪ SrSgn ()σ σ )vσ σ ()1)⊗ ⊗ ⋯ ⋯ ⊗ ⊗ vσ σ ()r){displaystyle operatorname {Alt} (v_{1}otimes cdots otimes v_{r}={frac {1} {r}}sum _{sigma in {mathfrak {S}_}operatorname {sgn} (sigma)v_{sigma (1)}otimes cdots otimes v_{sigma (r)}}}
donde se toma la suma sobre el grupo simétrico de permutaciones en los símbolos {1,... r}. Esto se extiende por linearidad y homogeneidad a una operación, también denotada por Alt, en el álgebra de tensor completo T(V). La imagen Alt(T(V) es el álgebra de tensor alterna, denotado A(V). Este es un subespacio vectorial de T(V), y hereda la estructura de un espacio vectorial de grado de que en T(V). Lleva un producto de grado asociativo ⊗ ⊗ ^ ^ {displaystyle {widehat {otimes}} definidas por
- t⊗ ⊗ ^ ^ s=Alt ()t⊗ ⊗ s).{displaystyle T~{widehat {otimes ♪♪♪♪ {Alt} (totimes s).}
Aunque este producto difiere del producto tensorial, el núcleo de Alt es precisamente el I ideal (nuevamente, suponiendo que K tiene características 0), y hay un isomorfismo canónico
- A()V).. ⋀ ⋀ ()V).{displaystyle A(V)cong {textstyle bigwedge }(V).}
Notación de índice
Suponga que V tiene dimensión finita n, y que una base e1,..., en de V. Entonces cualquier tensor alterno t ∈ Ar(V) ⊂ Tr(V) se puede escribir en notación de índice como
- t=ti1i2⋯ ⋯ irei1⊗ ⊗ ei2⊗ ⊗ ⋯ ⋯ ⊗ ⊗ eir,{displaystyle t=t^{i_{1}i_{2}cdots ¿Qué? #### ############################################################################################################################################################################################################################################################ }_{i_{2}otimes cdots otimes {mathbf {e} }
donde ti1⋅⋅⋅ir es completamente antisimétrico en sus índices.
El producto exterior de dos tensores alternos t y s de rangos r y p viene dado por
- t⊗ ⊗ ^ ^ s=1()r+p)!.. σ σ ▪ ▪ Sr+pSgn ()σ σ )tiσ σ ()1)⋯ ⋯ iσ σ ()r)siσ σ ()r+1)⋯ ⋯ iσ σ ()r+p)ei1⊗ ⊗ ei2⊗ ⊗ ⋯ ⋯ ⊗ ⊗ eir+p.{displaystyle T~{widehat {otimes {fnMicrosoft Sans Serif}} {fnMicrosoft Sans Serif}}} {fnMicroc {1}} {fnMicroc} {fnMicrosoft Sans Serif} sum _{sigma in {mathfrak {S}_{r+p}cdots i_{sigma)s^{i_sigma (1)}cdots i_{sigma (r)}s^{i_sigma (r+1)cdots i_{sigma (r+p)}}}{mathbfe} {cdot}} {cdots}} {cdots}}} {cdotsigma} {cdots} {cdotsg} {cdots} {cdots} {cdots} {cdots} {cdotsg} {cdotsg} {cdotsg} {cdots} {cdots} {cdots}cdots} {cdotsg} {cdotcdot}cdotcdotsg}cdot}cdot} }_{i_{1}otimes {mathbf {e} }_{i_{2}otimes cdots otimes {mathbf {e} - Sí.
Las componentes de este tensor son precisamente la parte sesgada de las componentes del producto tensorial s ⊗ t, indicado por corchetes en los índices:
- ()t⊗ ⊗ ^ ^ s)i1⋯ ⋯ ir+p=t[i1⋯ ⋯ irsir+1⋯ ⋯ ir+p].{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}cdots} ¿Qué? ¿Qué? - Sí.
El producto interior también se puede describir en la notación de índice como sigue. Vamos t=ti0i1⋯ ⋯ ir− − 1{displaystyle t=t^{i_{0}i_{1}cdots i_{r-1}} ser un tensor antisimétrico de rango r. Entonces, por α ▪ VAlternativa, iαt es un tensor alterna de rango r − 1, dado por
- ()iα α t)i1⋯ ⋯ ir− − 1=r.. j=0nα α jtji1⋯ ⋯ ir− − 1.{displaystyle (i_{alpha }t)}{i_{1}cdots i_{r-1}=rsum _{j=0} {n}alpha ¿Qué? Yo...
donde n es la dimensión de V.
Dualidad
Operadores alternos
Dados dos espacios vectoriales V y X y un número natural k, un operador alterno de Vk a X es un mapa multilineal
- f:: Vk→ → X{displaystyle fcolon V^{k}to X.
tal que siempre que v1,..., vk son vectores linealmente dependientes en V, entonces
- f()v1,...... ,vk)=0.{displaystyle f(v_{1},ldotsv_{k}=0.}
El mapa
- w:: Vk→ → ⋀ ⋀ k()V){displaystyle wcolon V^{k}to {textstyle bigwedge }{k}(V)}
que se asocia a k{displaystyle k} vectores de V{displaystyle V} su producto exterior, es decir, su correspondiente producto k{displaystyle k}-vector, también está alternando. De hecho, este mapa es el operador alternativo "más general" definido en Vk;{displaystyle V^{k};} dado cualquier otro operador alternativo f:Vk→ → X,{displaystyle F:V^{k}rightarrow X. existe un mapa lineal único φ φ :∧ ∧ k()V)→ → X{displaystyle phi:wedge ^{k}(V)rightarrow X} con f=φ φ ∘ ∘ w.{displaystyle f=phi circ w.} Esta propiedad universal caracteriza el espacio ∧ ∧ k()V){displaystyle wedge ^{k}(V)} y puede servir como su definición.
Formas multilineales alternas
La discusión anterior se especializa en el caso cuando X = K, el campo base. En este caso una función multilineal alterna
- f:Vk→ → K{displaystyle f:V^{k}to K.
se llama forma multilineal alternada. El conjunto de todas las formas multilineales alternantes es un espacio vectorial, ya que la suma de dos mapas tales, o el producto de tal mapa con un escalar, se alterna de nuevo. Por la propiedad universal de la potencia exterior, el espacio de formas alternas de grado k on V es naturalmente isomorfo con el espacio vectorial dual ()⋀ ⋀ k()V))Alternativa Alternativa .{biglstyle {bigl (}bigwedge nolimits ^{k}(V){bigr)}^{*}} Si V es finito-dimensional, entonces este último es naturalmente isomorfo a ⋀ ⋀ k()VAlternativa Alternativa ).{textstyle bigwedge nolimits ^{k}left(V^{*}right).} En particular, si V es n-dimensional, la dimensión del espacio de mapas alternados de Vk a K es el coeficiente binomio ()nk).{fnMicrosoft} {n}{k}.}
Bajo tal identificación, el producto exterior toma una forma concreta: produce un nuevo mapa antisimétrico a partir de dos dados. Supongamos que ω: Vk → K y η: Vm → K son dos mapas antisimétricos. Como en el caso de los productos tensoriales de aplicaciones multilineales, el número de variables de su producto exterior es la suma de los números de sus variables. En función de la elección de la identificación de elementos de potencia exterior con formas multilineales, el producto exterior se define como
- ⋅ ⋅ ∧ ∧ .. =Alt ()⋅ ⋅ ⊗ ⊗ .. ){displaystyle omega wedge eta =operatorname {Alt} (omega otimes eta)}
o como
- ⋅ ⋅ ∧ ∧ .. =()k+m)!k!m!Alt ()⋅ ⋅ ⊗ ⊗ .. ),{displaystyle omega wedge eta {fnMicrosoft Sans Serif}fnMicrosoft Sans Serif} {Alt} (omega otimes eta),}
donde, si la característica del campo base K es 0, la alternancia Alt de un mapa multilineal se define como el promedio de los valores ajustados por signo sobre todas las permutaciones de sus variables:
- Alt ()⋅ ⋅ )()x1,...... ,xk)=1k!.. σ σ ▪ ▪ SkSgn ()σ σ )⋅ ⋅ ()xσ σ ()1),...... ,xσ σ ()k)).{displaystyle operatorname (omega)(x_{1},ldotsx_{k}={frac {1} {k}}sum _{sigma in S_{k}operatorname {sgn}sigma),omega (x_{sigma (1)},ldotsx_{sigma (k)}). }
Cuando el campo K tiene una característica finita, una versión equivalente de la segunda expresión sin factoriales ni constantes está bien definida:
- ⋅ ⋅ ∧ ∧ .. ()x1,...... ,xk+m)=.. σ σ ▪ ▪ Shk,mSgn ()σ σ )⋅ ⋅ ()xσ σ ()1),...... ,xσ σ ()k)).. ()xσ σ ()k+1),...... ,xσ σ ()k+m)),{displaystyle {omega wedge eta (x_{1},ldotsx_{k+m}=sum _{sigma in mathrm {Sh} _{k,m}operatorname {sgn} (sigma),omega (x_{sigma (1)},ldotsx_{sigma (k)}),eta (x_{sigma (k+1)},ldotsx_{sigma (k+m)}}}})})}
donde aquí Shk,m ⊂ S k+m es el subconjunto de (k,m) baraja: permutaciones σ del conjunto {1, 2,..., k + m} tal que σ(1) < σ(2) < ⋯ < σ(k), y σ(k + 1) < σ(k + 2) < ⋯ < σ(k + m).
Producto para interiores
Supongamos que V es finito-dimensional. Si VAlternativa denota el espacio dual al espacio vectorial V, entonces para cada α ▪ VAlternativa, es posible definir una antiderivación en el álgebra ⋀ ⋀ ()V),{textstyle bigwedge (V),}
- iα α :⋀ ⋀ kV→ → ⋀ ⋀ k− − 1V.{displaystyle i_{alpha }:{textstyle bigwedge }{k} Vrightarrow {textstyle bigwedge V.
Esta derivación se denomina producto interior con α, o a veces operador de inserción, o contracción por α.
Supongamos que w▪ ▪ ⋀ ⋀ kV.{textstyle win bigwedge nolimits ^{k} V.} Entonces... w es un mapeo multilineal VAlternativa a K, por lo que se define por sus valores en k- producto cartesiano VAlternativa × VAlternativa ×... × VAlternativa. Si u1, u2,... uk−1 son k − 1 elementos VAlternativa, entonces definir
- ()iα α w)()u1,u2,...... ,uk− − 1)=w()α α ,u1,u2,...... ,uk− − 1).{displaystyle (i_{alpha }{mathbf {w})(u_{1},u_{2},ldotsu_{k-1})={mathbf {w}(alphau_{1},u_{2},ldotsu_{k-1}). }
Además, iαf = 0 siempre f es un cuero cabelludo puro (es decir, perteneciente a ⋀ ⋀ 0V{textstyle bigwedge nolimits ^{0}V}).
Caracterización axiomática y propiedades
El producto interior cumple con las siguientes propiedades:
- Para cada uno k y cada uno α ▪ VAlternativa, (Por convención, ⋀ ⋀ − − 1V={}0}.{textstyle bigwedge nolimits ^{-1}V= {0})iα α :⋀ ⋀ kV→ → ⋀ ⋀ k− − 1V.{displaystyle i_{alpha }:{textstyle bigwedge }{k} Vrightarrow {textstyle bigwedge V.
- Si v es un elemento V ()=⋀ ⋀ 1V{textstyle =bigwedge nolimits ^{1}V}), entonces iαv = α()v) es la unión dual entre elementos de V y elementos de VAlternativa.
- Para cada uno α ▪ VAlternativa, iα es una derivación de grado −1:iα α ()a∧ ∧ b)=()iα α a)∧ ∧ b+()− − 1)deg aa∧ ∧ ()iα α b).{displaystyle i_{alpha }(awedge b)=(i_{alpha }a)wedge b+(-1)^{deg a}awedge (i_{alpha }b).}
Estas tres propiedades son suficientes para caracterizar el producto interior y definirlo en el caso general de dimensión infinita.
Otras propiedades del producto interior incluyen:
- iα α ∘ ∘ iα α =0.{displaystyle i_{alpha. i_{alpha }=0.}
- iα α ∘ ∘ iβ β =− − iβ β ∘ ∘ iα α .{displaystyle i_{alpha. I_{beta }=-i_{beta. }
Dualidad de Hodge
Supongamos que V tiene una dimensión finita n. Entonces el producto interior induce un isomorfismo canónico de espacios vectoriales
- ⋀ ⋀ k()VAlternativa Alternativa )⊗ ⊗ ⋀ ⋀ n()V)→ → ⋀ ⋀ n− − k()V){displaystyle {textstyle bigwedge }^{k}(V^{*})otimes {textstyle bigwedge }^{n}(V)to {textstyle bigwedge }^{n-k}(V)}}
por la definición recursiva
- iα α ∧ ∧ β β =iβ β ∘ ∘ iα α .{displaystyle i_{alpha wedge beta }=i_{beta. }
En el entorno geométrico, un elemento no cero de la potencia exterior superior ⋀ ⋀ n()V){textstyle bigwedge nolimits ^{n}(V)} (que es un espacio vectorial único) a veces se llama formulario de volumen (o formulario de orientación, aunque este término a veces puede conducir a la ambigüedad). El formulario de orientación del nombre proviene del hecho de que una elección del elemento superior preferido determina una orientación de todo el álgebra exterior, ya que es equivalente a fijar una base ordenada del espacio vectorial. Relativo a la forma de volumen preferida σ, el isomorfismo se da explícitamente
- ⋀ ⋀ k()VAlternativa Alternativa )→ → ⋀ ⋀ n− − k()V):α α ↦ ↦ iα α σ σ .{displaystyle {textstyle bigwedge }{k}(V^{*}to {textstyle bigwedge }^{n-k}(V):alpha mapsto i_{alpha }sigma.}
Si, además de una forma de volumen, el espacio vectorial V está equipado con un producto interior que identifica V con V ∗, el isomorfismo resultante se denomina operador estrella de Hodge, que asigna un elemento a su dual de Hodge:
- ⋆ ⋆ :⋀ ⋀ k()V)→ → ⋀ ⋀ n− − k()V).{displaystyle star:{textstyle bigwedge }^{k}(V)rightarrow {textstyle bigwedge }{n-k}(V).}
La composición ⋆ ⋆ {displaystyle star } con mapas propios ⋀ ⋀ k()V){textstyle bigwedge nolimits ^{k}(V)} → ⋀ ⋀ k()V){textstyle bigwedge nolimits ^{k}(V)} y siempre es un escalar múltiple del mapa de identidad. En la mayoría de las aplicaciones, la forma de volumen es compatible con el producto interno en el sentido de que es un producto exterior de una base ortonormal de V. En este caso,
- ⋆ ⋆ ∘ ∘ ⋆ ⋆ :⋀ ⋀ k()V)→ → ⋀ ⋀ k()V)=()− − 1)k()n− − k)+qid{displaystyle star circ star:{textstyle bigwedge }^{k}(V)to {textstyle bigwedge }^{k}(V)=(-1)^{k(n-k)+q}mathrm {id} }
donde id es el mapeo de identidad, y el producto interno tiene una firma métrica (p, q) — p más y q menos.
Producto interior
Para V un espacio finito-dimensional, un producto interno (o un producto interior pseudo-euclidiano) en V define un isomorfismo de V con VAlternativa, y así también un isomorfismo ⋀ ⋀ kV{textstyle bigwedge nolimits ^{k}V} con ()⋀ ⋀ kV)Alternativa Alternativa .{biglstyle {bigl (}bigwedge nolimits ^{k}V{bigr)}^{*}} El emparejamiento entre estos dos espacios también toma la forma de un producto interno. Sobre descompuesto k- Véctores,
- .v1∧ ∧ ⋯ ⋯ ∧ ∧ vk,w1∧ ∧ ⋯ ⋯ ∧ ∧ wk.=Det().. vi,wj.. ),{displaystyle leftlangle v_{1}wedge cdots wedge {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}
el determinante de la matriz de los productos internos. En el caso especial vi = wi, el producto interior es la norma cuadrada de la k-vector, dado por el determinante de la matriz gramiana #vi, vj.. Esto se extiende bilinealmente (o sesquilinealmente en el caso complejo) a un producto interno no degenerado en ⋀ ⋀ kV.{textstyle bigwedge nolimits ^{k} V.} Si ei, i = 1, 2,... n, formar una base ortonormal de V, entonces los vectores de la forma
- <math alttext="{displaystyle e_{i_{1}}wedge cdots wedge e_{i_{k}},quad i_{1}<cdots ei1∧ ∧ ⋯ ⋯ ∧ ∧ eik,i1.⋯ ⋯ .ik,{displaystyle e_{i_{1}wedge cdots wedge e_{i_{k},quad i_{1} - No.<img alt="{displaystyle e_{i_{1}}wedge cdots wedge e_{i_{k}},quad i_{1}<cdots
constituye una base ortonormal para ⋀ ⋀ k()V){textstyle bigwedge nolimits ^{k}(V)}, una declaración equivalente a la fórmula Cauchy-Binet.
Con respecto al producto interno, la multiplicación exterior y el producto interior son mutuamente unidos. Específicamente, para v▪ ▪ ⋀ ⋀ k− − 1()V),{textstyle vin bigwedge nolimits ^{k-1}(V),} w▪ ▪ ⋀ ⋀ k()V),{textstyle win bigwedge nolimits ^{k}(V),} y x▪ ▪ V,{textstyle xin V,}
- .. x∧ ∧ v,w.. =.. v,ix.. w.. {displaystyle langle xwedge mathbf {v}mathbf {w} rangle =langle mathbf {fnMicrosoft} rangle }
donde x♭ ∈ V∗ es el isomorfismo musical, el funcional lineal definido por
- x.. ()Sí.)=.. x,Sí... {displaystyle x^{flat }(y)=langle x,yrangle }
para todos los y ∈ V. Esta propiedad caracteriza completamente el producto interior sobre el álgebra exterior.
De hecho, más generalmente para v▪ ▪ ⋀ ⋀ k− − l()V),{textstyle vin bigwedge nolimits ^{k-l}(V),} w▪ ▪ ⋀ ⋀ k()V),{textstyle win bigwedge nolimits ^{k}(V),} y x▪ ▪ ⋀ ⋀ l()V),{textstyle xin bigwedge nolimits ^{l}(V),} iteración de las propiedades adyacentes anteriores da
- .. x∧ ∧ v,w.. =.. v,ix.. w.. {displaystyle langle mathbf {x} wedge mathbf {v}mathbf {w} rangle =langle mathbf {v}i_{mathbf {x} ^{flat }mathbf {w} rangle }
donde ahora x.. ▪ ▪ ⋀ ⋀ l()VAlternativa Alternativa )≃ ≃ ()⋀ ⋀ l()V))Alternativa Alternativa {textstyle x^{flat }in bigwedge nolimits ^{l}left(V^{*}right)simeq {bigl (}bigwedge nolimits ^{l}(V){bigr)}}{*}}}}}}}}}} es el doble l-vector definido
- x.. ()Sí.)=.. x,Sí... {displaystyle mathbf {x} {flat }(mathbf {y})=langle mathbf {x}mathbf {y}rangle }
para todos Sí.▪ ▪ ⋀ ⋀ l()V).{textstyle yin bigwedge nolimits ^{l}(V).}
Estructura biálgebra
Hay una correspondencia entre el doble grado del álgebra de grado ⋀ ⋀ ()V){textstyle bigwedge (V)} y formas multilineales alternadas en V. El álgebra exterior (así como el álgebra simétrica) hereda una estructura biálgebra, y, de hecho, una estructura álgebra Hopf, del álgebra tensor. Vea el artículo sobre álgebras de tensor para un tratamiento detallado del tema.
El producto exterior de formas multilineales definidas anteriormente es dual a un coproducto definido en ⋀ ⋀ ()V),{textstyle bigwedge (V),} dando la estructura de un álgebra. El coproduct es una función lineal Δ: ⋀ ⋀ ()V){textstyle bigwedge (V)} → ⋀ ⋀ ()V){textstyle bigwedge (V)} ⊗ ⋀ ⋀ ()V){textstyle bigwedge (V)} que se da por
- Δ Δ ()v)=1⊗ ⊗ v+v⊗ ⊗ 1{displaystyle Delta (v)=1otimes v+votimes 1}
sobre elementos v▪V. El símbolo 1 representa el elemento unitario del campo K. Recordad que K ⊂ ⋀ ⋀ ()V){textstyle bigwedge (V)}, para que lo anterior realmente miente ⋀ ⋀ ()V){textstyle bigwedge (V)} ⊗ ⋀ ⋀ ()V){textstyle bigwedge (V)}. Esta definición del coproducto se levanta al espacio completo ⋀ ⋀ ()V){textstyle bigwedge (V)} por (linear) homomorfismo. La forma correcta de este homomorfismo no es lo que uno podría escribir ingenuamente, sino que tiene que ser el cuidadosamente definido en el artículo del álgebra. En este caso, se obtiene
- Δ Δ ()v∧ ∧ w)=1⊗ ⊗ ()v∧ ∧ w)+v⊗ ⊗ w− − w⊗ ⊗ v+()v∧ ∧ w)⊗ ⊗ 1.{displaystyle Delta (vwedge w)=1otimes (vwedge w)+votimes w-wotimes v+(vwedge w)otimes 1.}
Expandiendo esto en detalle, se obtiene la siguiente expresión sobre elementos descomponibles:
- Δ Δ ()x1∧ ∧ ⋯ ⋯ ∧ ∧ xk)=.. p=0k.. σ σ ▪ ▪ Sh()p+1,k− − p)Sgn ()σ σ )()xσ σ ()0)∧ ∧ ⋯ ⋯ ∧ ∧ xσ σ ()p))⊗ ⊗ ()xσ σ ()p+1)∧ ∧ ⋯ ⋯ ∧ ∧ xσ σ ()k)).{displaystyle Delta (x_{1}wedge cdots wedge x_{k})=sum _{p=0}\;sum _{sigmain Sh(p+1,k-p)};operatorname {sgn}(sigma)(x_{sigma (0)}edoge }
donde se toma la segunda suma sobre todos (p+1, k−p)-shuffles. Lo anterior está escrito con un truco notacional, para hacer un seguimiento del elemento de campo 1: el truco es escribir x0=1,{displaystyle x_{0}=1,} y esto se deslumbra en varios lugares durante la expansión de la suma sobre los arbustos. El shuffle sigue directamente desde el primer axioma de un álgebra: el orden relativo de los elementos xk{displaystyle x_{k} es preservados en el riffle shuffle: el riffle shuffle simplemente divide la secuencia ordenada en dos secuencias ordenadas, una a la izquierda, y una a la derecha.
Observe que el coproducto preserva la clasificación del álgebra. Ampliación al espacio completo ⋀ ⋀ ()V),{textstyle bigwedge (V),} uno tiene
- Δ Δ :⋀ ⋀ k()V)→ → ⨁ ⨁ p=0k⋀ ⋀ p()V)⊗ ⊗ ⋀ ⋀ k− − p()V){displaystyle Delta:{textstyle bigwedge }^{k}(V)to bigoplus _{p=0}^{k}{textstyle bigwedge }^{p}(V)otimes {textstyle bigwedge }^{k-p}(V)}}
El símbolo tensor ⊗ utilizado en esta sección debe ser entendido con cierta precaución: es no el mismo símbolo tensor que el que se utiliza en la definición del producto alternante. Intuitivamente, es quizás más fácil pensarlo como otro, pero diferente, producto tensor: es todavía (bi-)linear, como los productos tensores deben ser, pero es el producto que es apropiado para la definición de un bialgebra, es decir, para crear el objeto ⋀ ⋀ ()V){textstyle bigwedge (V)} ⊗ ⋀ ⋀ ()V){textstyle bigwedge (V)}. Cualquier duda persistente puede ser sacudida al reflexionar sobre las igualdades (1 ⊗) v) ∧ (1 ⊗ w= 1 ⊗v ∧ w) y ()v ⊗ 1) ∧ (1 ⊗ w) v ⊗ w, que sigue de la definición del álgebra, en lugar de manipulaciones ingenuas que implican el tensor y símbolos de cuña. Esta distinción se desarrolla en mayor detalle en el artículo sobre álgebras tensoras. Aquí, hay mucho menos de un problema, en que el producto alternativo ∧ claramente corresponde a la multiplicación en el bialgebra, dejando el símbolo ⊗ libre para uso en la definición del bialgebra. En la práctica, esto no presenta ningún problema en particular, siempre y cuando se evite la trampa mortal de sustituir las sumas alternas de ⊗ por el símbolo de cuña, con una excepción. Uno puede construir un producto alternativo de ⊗, con el entendimiento de que funciona en un espacio diferente. Inmediatamente a continuación se da un ejemplo: el producto alternativo para el espacio dual se puede dar en términos del coproducto. La construcción del biálgebra aquí paralela la construcción en el artículo de álgebra de tensor casi exactamente, excepto por la necesidad de rastrear correctamente los signos alternantes para el álgebra exterior.
En términos del coproducto, el producto exterior en el espacio dual es solo el dual graduado del coproducto:
- ()α α ∧ ∧ β β )()x1∧ ∧ ⋯ ⋯ ∧ ∧ xk)=()α α ⊗ ⊗ β β )()Δ Δ ()x1∧ ∧ ⋯ ⋯ ∧ ∧ xk)){displaystyle (alpha wedge beta)(x_{1}wedge cdots wedge x_{k})=(alpha otimes beta)left(Delta (x_{1}wedge cdots wedge x_{k})right)}
donde el producto tensorial del lado derecho es de mapas lineales multilineales (extendidos por cero en elementos de grado homogéneo incompatible: más precisamente, α ∧ β = ε ∘ (α ⊗ β) ∘ Δ, donde ε es el país, tal como se define actualmente).
El counit es el homomorfismo ε: ⋀ ⋀ ()V){textstyle bigwedge (V)} → K que devuelve el componente de 0 grados de su argumento. El coproducto y la counidad, junto con el producto exterior, definen la estructura de un biálgebra en el álgebra exterior.
Con una antipodos definidos en elementos homogéneos por S()x)=()− − 1)()degx+12)x,{displaystyle S(x)=(-1)^{binom ################################################################################################################################################################################################################################################################ el álgebra exterior es además un álgebra Hopf.
Funcionalidad
Supongamos que V y W son un par de espacios vectoriales y f: V → W es un mapa lineal. Entonces, por la propiedad universal, existe un único homomorfismo de álgebras graduadas
- ⋀ ⋀ ()f):⋀ ⋀ ()V)→ → ⋀ ⋀ ()W){displaystyle {textstyle bigwedge }(f):{textstyle bigwedge }(V)rightarrow {textstyle bigwedge }(W)}
tal que
- ⋀ ⋀ ()f)Silencio⋀ ⋀ 1()V)=f:V=⋀ ⋀ 1()V)→ → W=⋀ ⋀ 1()W).{displaystyle {textstyle bigwedge }(f)left forever_{textstyle bigwedge }^{1}(V)}right.=f:V={textstyle bigwedge }^{1}(V)rightarrow W={textstyle bigwedge }^{1}(W).}
En particular, ⋀ ⋀ ()f){textstyle bigwedge left(fright)} conserva un grado homogéneo. El k- componentes de grado ⋀ ⋀ ()f){textstyle bigwedge left(fright)} se dan sobre elementos descompuestos por
- ⋀ ⋀ ()f)()x1∧ ∧ ⋯ ⋯ ∧ ∧ xk)=f()x1)∧ ∧ ⋯ ⋯ ∧ ∧ f()xk).{displaystyle {textstyle bigwedge }(f)(x_{1}wedge cdots wedge x_{k})=f(x_{1})wedge cdots wedge f(x_{k}). }
Dejar
- ⋀ ⋀ k()f)=⋀ ⋀ ()f)Silencio⋀ ⋀ k()V):⋀ ⋀ k()V)→ → ⋀ ⋀ k()W).{displaystyle {textstyle bigwedge }{k}(f)={textstyle bigwedge }(f)left WordPress_{textstyle bigwedge }^{k}(V)}right.:{textstyle bigwedge }{k}(V)rightarrow {textstylebigwedge }
Los componentes de la transformación ⋀ ⋀ k()f){textstyle bigwedge nolimits ^{k}left(fright)} relativa a una base de V y W es la matriz k × k menores de edad f. En particular, si V = W y V es de dimensión finita n, entonces ⋀ ⋀ n()f){textstyle bigwedge nolimits ^{n}left(fright)} es un mapeo de un espacio vectorial único ⋀ ⋀ n()V){textstyle bigwedge nolimits ^{n}(V)} a sí mismo, y es dado por un escalar: el determinante f.
Exactitud
Si 0→ → U→ → V→ → W→ → 0{displaystyle 0to Uto Vto Wto 0} es una breve secuencia exacta de espacios vectoriales, entonces
- 0→ → ⋀ ⋀ 1()U)∧ ∧ ⋀ ⋀ ()V)→ → ⋀ ⋀ ()V)→ → ⋀ ⋀ ()W)→ → 0{displaystyle 0to {textstyle bigwedge }^{1}(U)wedge {textstyle bigwedge }(V)to {textstyle bigwedge }(V)to {to {textstyle bigwedge }(W)to 0}
es una secuencia exacta de espacios vectoriales graduados, como lo es
- 0→ → ⋀ ⋀ ()U)→ → ⋀ ⋀ ()V).{textstyle 0to bigwedge (U)to bigwedge (V). }
Sumas directas
En particular, el álgebra exterior de una suma directa es isomorfa al producto tensorial de las álgebras exteriores:
- ⋀ ⋀ ()V⊕ ⊕ W).. ⋀ ⋀ ()V)⊗ ⊗ ⋀ ⋀ ()W).{displaystyle {textstyle bigwedge }(Voplus W)cong {textstyle bigwedge }(V)otimes {textstyle bigwedge }(W).}
Este es un isomorfismo graduado; es decir.,
- ⋀ ⋀ k()V⊕ ⊕ W).. ⨁ ⨁ p+q=k⋀ ⋀ p()V)⊗ ⊗ ⋀ ⋀ q()W).{displaystyle {textstyle bigwedge }^{k}(Voplus W)cong bigoplus _{p+q=k}{textstyle bigwedge }{p}(V)otimes {textstyle bigwedge }^{q}(W).}
En mayor generalidad, para una breve secuencia exacta de espacios vectoriales 0→ → U→ → fV→ → gW→ → 0,{textstyle 0to Umathrel {overset {f}{to } Vmatrel {overset {g}Wto 0,} hay una filtración natural
- 0=F0⊆ ⊆ F1⊆ ⊆ ⋯ ⋯ ⊆ ⊆ Fk⊆ ⊆ Fk+1=⋀ ⋀ k()V){displaystyle 0=F^{0}subseteq F^{1}subseteq cdots subseteq F^{k}subseteq F^{k+1}={textstyle bigwedge }^{k}(V)}
Donde Fp{displaystyle F^{p} para p≥ ≥ 1{displaystyle pgeq 1} es abarcado por elementos de la forma u1∧ ∧ ...... ∧ ∧ uk+1− − p∧ ∧ v1∧ ∧ ...... vp− − 1{displaystyle u_{1}wedge ldots wedge u_{k+1-p}wedge v_{1}wedge ldots v_{p-1} para ui▪ ▪ U{displaystyle u_{i}in U} y vi▪ ▪ V.{displaystyle v_{i}in V.}Los cocientes correspondientes admiten un isomorfismo natural
- Fp+1/Fp.. ⋀ ⋀ k− − p()U)⊗ ⊗ ⋀ ⋀ p()W){displaystyle F^{p+1}/F^{p}cong {textstyle bigwedge }^{k-p}(U)otimes {textstyle bigwedge }^{p}(W)} dado por u1∧ ∧ ...... ∧ ∧ uk− − p∧ ∧ v1∧ ∧ ...... ∧ ∧ vp↦ ↦ u1∧ ∧ ...... ∧ ∧ uk− − p⊗ ⊗ g()v1)∧ ∧ ...... ∧ ∧ g()vp).{displaystyle u_{1}wedge ldots wedge u_{k-p}wedge v_{1}wedge ldots wedge v_{p}mapsto u_{1}wedge ldots wedge u_{k-p}otimes g(v_{1})wedge ldots }
En particular, si U es unidimensional, entonces
- 0→ → U⊗ ⊗ ⋀ ⋀ k− − 1()W)→ → ⋀ ⋀ k()V)→ → ⋀ ⋀ k()W)→ → 0{displaystyle 0to Uotimes {textstyle bigwedge }^{k-1}(W)to {textstyle bigwedge }^{k}(V)to {textstyle bigwedge }^{k}(W)to 0}
es exacta, y si W es unidimensional, entonces
- 0→ → ⋀ ⋀ k()U)→ → ⋀ ⋀ k()V)→ → ⋀ ⋀ k− − 1()U)⊗ ⊗ W→ → 0{displaystyle 0to {textstyle bigwedge }^{k}(U)to {textstyle bigwedge }^{k}(V)to {textstyle bigwedge }{k-1}(U)otimes Wto 0}
es exacto.
Aplicaciones
Álgebra lineal
En aplicaciones al álgebra lineal, el producto exterior proporciona una forma algebraica abstracta para describir el determinante y los menores de una matriz. Por ejemplo, es bien sabido que el determinante de una matriz cuadrada es igual al volumen del paralelotopo cuyos lados son las columnas de la matriz (con un signo para seguir la orientación). Esto sugiere que el determinante se puede definir en términos del producto exterior de los vectores columna. Del mismo modo, los k × k menores de una matriz se pueden definir observando los productos exteriores de los vectores columna elegidos k a la vez. Estas ideas se pueden extender no solo a las matrices, sino también a las transformaciones lineales: el determinante de una transformación lineal es el factor por el cual escala el volumen orientado de cualquier paralelotopo de referencia dado. Entonces, el determinante de una transformación lineal se puede definir en términos de lo que la transformación le hace a la potencia exterior superior. La acción de una transformación sobre las potencias exteriores menores da una forma independiente de base para hablar de las menores de la transformación.
Detalles técnicos: Definiciones
Vamos V{displaystyle V} ser un n-dimensional espacio vectorial sobre el campo K{displaystyle K} con base {}e1,...... ,en}.{displaystyle {e_{1},ldotse_{n}}
- Para A▪ ▪ Final ()V),{displaystyle Ain operatorname {End} (V),} definir ⋀ ⋀ kA▪ ▪ Final ()⋀ ⋀ kV){textstyle bigwedge ^{k} Ain operatorname {End} {bigl (}bigwedge ^{k}V{bigr)} en simples tensores por y ampliar la definición linealmente a todos los tensores. Más generalmente, podemos definir ⋀ ⋀ pAk▪ ▪ Final ()⋀ ⋀ pV),()p≥ ≥ k){textstyle bigwedge ^{p}A^{k}in operatorname {End} {bigl (}bigwedge ^{p}V{bigr)},(pgeq k)} en simples tensores por⋀ ⋀ kA()v1∧ ∧ ⋯ ⋯ ∧ ∧ vk)=Av1∧ ∧ ⋯ ⋯ ∧ ∧ Avk{displaystyle {textstyle bigwedge }{k}A(v_{1}wedge cdots wedge v_{k})=Av_{1}wedge cdots wedge Av_{k}i.e. elija k componentes sobre los cuales A actuaría, luego sumaría todos los resultados obtenidos de diferentes opciones. Si <math alttext="{displaystyle pp.k,{displaystyle P:<img alt="{displaystyle p definir ⋀ ⋀ pAk=0.{textstyle bigwedge ^{p}A^{k}=0.} Desde ⋀ ⋀ nV{textstyle bigwedge ^{n}V} es 1-dimensional con base e1∧ ∧ ⋯ ⋯ ∧ ∧ en,{displaystyle e_{1}wedge cdots wedge e_{n} podemos identificar ⋀ ⋀ nAk{textstyle bigwedge ^{n} A^{k} con el número único κ κ ▪ ▪ K{displaystyle kappa in K} satisfacción<math alttext="{displaystyle {begin{aligned}&left({textstyle bigwedge }^{p}A^{k}right)(v_{1}wedge cdots wedge v_{p})\[10mu]&qquad =sum _{0leq i_{1}<cdots ()⋀ ⋀ pAk)()v1∧ ∧ ⋯ ⋯ ∧ ∧ vp)=.. 0≤ ≤ i1.⋯ ⋯ .ik≤ ≤ pv1∧ ∧ ⋯ ⋯ ∧ ∧ Avi1∧ ∧ ⋯ ⋯ ∧ ∧ Avik∧ ∧ ⋯ ⋯ ∧ ∧ vp{displaystyle {begin{aligned} limiteleft({textstyle bigwedge }^{p}A^{k}right)(v_{1}wedge cdots wedge v_{p})[10mu] =sum _{0leq i_{1}cdots hechos i_{k}leq p}v_{1}wedge cdots wedge Av_{i_{1}wedge cdots wedge Av_{i_{k}wedge cdots wedge v_{p}end{aligned}}<img alt="{displaystyle {begin{aligned}&left({textstyle bigwedge }^{p}A^{k}right)(v_{1}wedge cdots wedge v_{p})\[10mu]&qquad =sum _{0leq i_{1}<cdots⋀ ⋀ nAk()e1∧ ∧ ⋯ ⋯ ∧ ∧ en)=κ κ ()e1∧ ∧ ⋯ ⋯ ∧ ∧ en).{displaystyle {textstyle bigwedge }^{n}A^{k}(e_{1}wedge cdots wedge e_{n})=kappa (e_{1}wedge cdots wedge e_{n}). }
- Para φ φ ▪ ▪ Final ()⋀ ⋀ pV),{displaystyle varphi in operatorname {End} {bigl (}{style bigwedge }{p}V{bigr)}}} definir transposeo exterior φ φ T▪ ▪ Final ()⋀ ⋀ n− − pV){textstyle varphi ^{mathrm {T}in operatorname {End} {bigl (}bigwedge ^{n-p}V{bigr)}} ser el operador único que satisface ()φ φ T⋅ ⋅ n− − p)∧ ∧ ⋅ ⋅ p=⋅ ⋅ n− − p∧ ∧ ()φ φ ⋅ ⋅ p){textstyle (varphi ^{mathrm {T}omega _{n-p})wedge omega ###{p}=omega ¿Por qué? para cualquier ⋅ ⋅ p▪ ▪ ⋀ ⋀ pV{textstyle omega _{p}in {textstyle bigwedge }{p}V} y ⋅ ⋅ n− − p▪ ▪ ⋀ ⋀ n− − pV.{textstyle omega ################################################################################################################################################################################################################################################################ } {n-p}V.}
- Para A▪ ▪ Final ()V),{displaystyle Ain operatorname {End} (V),} definir DetA=⋀ ⋀ nAn,{textstyle det A=bigwedge ^{n}A^{n} Tr ()A)=⋀ ⋀ nA1,{textstyle operatorname ¿Qué? adj A=()⋀ ⋀ n− − 1An− − 1)T.{textstyle operatorname {adj} A={bigl (}bigwedge ^{n-1}A^{n-1}{bigr)}{mathrm {T}}} Son equivalentes a las definiciones anteriores.
Propiedades básicas
Todos los resultados obtenidos de otras definiciones de determinante, traza y adjunto se pueden obtener de esta definición (ya que estas definiciones son equivalentes). Aquí hay algunas propiedades básicas relacionadas con estas nuevas definiciones:
- ()⋅ ⋅ )T{displaystyle (cdot)^{mathrm {T} es K{displaystyle K}- lineal.
- ()AB)T=BTAT.{displaystyle (AB)^{mathrm {T}=B^{mathrm {T}A^{mathrm {T}}
- Tenemos un isomorfismo canónico Sin embargo, no hay isomorfismo canónico entre ⋀ ⋀ kV{textstyle bigwedge ^{k}V} y ⋀ ⋀ n− − kV.{textstyle bigwedge ^{n-k}V.}{}↑ ↑ :Final ()⋀ ⋀ kV).. Final ()⋀ ⋀ n− − kV)A↦ ↦ AT{displaystyle {begin{cases}psi:operatorname {End} {bigl (}{style bigwedge }{k}V{bigr)}cong operatorname {End} {bigl (}{style bigwedge }{n-k}V{bigr)}\ Amapsto A^{mathrm {T}end{cases}
- Tr ()⋀ ⋀ kA)=⋀ ⋀ nAk.{textstyle operatorname {Tr} {bigl (}bigwedge ^{k}A{bigr)}= Bigwedge. Las entradas de la matriz transpuesta ⋀ ⋀ kA{textstyle bigwedge ^{k} A} son k× × k{displaystyle ktimes k}- las minas de A.{displaystyle A.}
- Para todos k≤ ≤ n− − 1,p≤ ≤ k,A▪ ▪ Final ()V),{displaystyle kleq n-1,pleq k,Ain operatorname {End} (V),} En particular,.. q=0p()⋀ ⋀ n− − kAp− − q)T()⋀ ⋀ kAq)=()⋀ ⋀ nAp)Id▪ ▪ Final ()V).{big} {big}{bigr} {big} {big}} {big}} {big}} {big} {big}} {big}} {big}} {big} {big}}} {big} {big}big}}{big}{big}{big}{big}{big}}{big}big}}{big}{big}{big}}}{big}{big}{}{big}big}big}}}{}{big}{big}{big}{}{big}{big}big}{}{}big}big}big}}}}{}{}{}{}{big}}}big}{}{}}}}}}}}}}}}} {Id} in operatorname {End} (V). }y por consiguiente()⋀ ⋀ n− − 1Ap− − 1)TA+()⋀ ⋀ n− − 1Ap)T=()⋀ ⋀ nAp)Id{displaystyle {bigl (}{textstyle bigwedge }{n-1}A^{p-1}{bigr)}{mathrm {T}A+{bigl (}{textstyle bigwedge }{n-1}A^{p}{bigr}}{mathrm {}={bigl (}{textstyle bigwedge - ¿Qué? {Id}()adj A)A=()⋀ ⋀ n− − 1An− − 1)TA=()⋀ ⋀ nAn)Id=()DetA)Id.{displaystyle (operatorname {adj} A)A={bigl (}{textstyle bigwedge }^{n-1}A^{n-1}{bigr)}{mathrm {T}A={bigl (}{textstyle bigwedge } {n}A^{n}{bigr)}operatorname {Id} =(det A)operatorname {Id}
- ()⋀ ⋀ n− − 1Ap)T=.. q=0p()⋀ ⋀ nAp− − q)()− − A)q=.. q=0pTr ()⋀ ⋀ p− − qA)()− − A)q.{displaystyle {bigl (}{textstyle bigwedge }{n-1}A^{p}{bigr)}{mathrm {T}=sum ¿Por qué? ################################################################################################################################################################################################################################################################ {Tr} {bigl (}{style bigwedge }{p-q}A{bigr)}(-A)^{q} En particular, adj A=.. q=0n− − 1()⋀ ⋀ nAn− − q− − 1)()− − A)q.{displaystyle operatorname {adj} A=sum ##{q=0}{n-1}{bigl (}{textstyle bigwedge ¿Por qué?
- Tr ()⋀ ⋀ kadj A)=⋀ ⋀ n()adj A)k=()DetA)k− − 1()⋀ ⋀ nAn− − k)=()DetA)k− − 1Tr ()⋀ ⋀ n− − kA).{displaystyle operatorname {bigl (}{textstyle bigwedge ################################################################################################################################################################################################################################################################
- Tr()()⋀ ⋀ n− − 1Ak)T)=()n− − k)⋀ ⋀ nAp=()n− − k)Tr ()⋀ ⋀ pA).{displaystyle operatorname {Tr} !{Bigl (}{bigl (}{textstyle bigwedge }^{n-1}A^{k}{bigr)}{mathrm {} {Bigr)}=(n-k){textstylebigwedge } {n}A^p= {Tr} left({textstyle bigwedge }{p}Aright). }
- El polinomio característico chA ()t){displaystyle operatorname {ch} _{A}(t)} de A▪ ▪ Final ()V){displaystyle Ain operatorname {End} (V)} puede ser dado por Análogamente,chA ()t)=.. k=0nTr ()⋀ ⋀ kA)()− − t)n− − k=.. k=0n()⋀ ⋀ nAk)()− − t)n− − k.{displaystyle operatorname {ch} _{A}(t)=sum ################################################################################################################################################################################################################################################################ {Tr} {bigl (}{style bigwedge }{k}A{bigr)}(-t)^{n-k}=sum _{k=0} {n}left({textstyle bigwedge } {n}A^{k}right) {-t)}{n-k}} {} {}} {big}} {big}}}}}}}} {b} {b} {b}}} {b} {b}}}}}}} {b} {b} {b}} {b} {b}}}}}}} {b} {b}}} {b} {b} {b} {b} {b}}}} {b}}}}}}}}}} {b}}}}}}}}} {b}}}} {b}}}}}}}}}} {b}}}}}}chadj A ()t)=.. k=0n()⋀ ⋀ n()adj A)k)()− − t)n− − k=.. k=0n()DetA)k− − 1()⋀ ⋀ nAn− − k)()− − t)n− − k{cHFF} {cHFF} {cHFF} {cHFF} {ccHFF} {cHFF} {ccHFF} {ccHFF} {cHFF} {cHFF} {cHFF}} {cHFF}}}}} {cHFF}} {c}}}}}}}} {f}}}}} {f}}}}}} {cccccccc}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {ccccccccccccccccccc}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}
Algoritmo de Leverrier
⋀ ⋀ nAk{textstyle bigwedge ^{n} A^{k} son los coeficientes de los ()− − t)n− − k{displaystyle (-t)} {n-k} términos en el polinomio característico. También aparecen en las expresiones de ()⋀ ⋀ n− − 1Ap)T{bign-1} {bigr} {bigr} {bigr}}} {mhm}}} y ⋀ ⋀ n()adj A)k.{textstyle bigwedge ^{n}(operatorname {adj} A)^{k} Algoritmo de Leverrier es una forma económica de computación ⋀ ⋀ nAk{textstyle bigwedge ^{n} A^{k} y ⋀ ⋀ n− − 1Ak:: {textstyle bigwedge - ¿Qué?
- Set ⋀ ⋀ n− − 1A0=1;{textstyle bigwedge ^{n-1}A^{0}=1;}
- Para k=n− − 1,n− − 2,...... ,1,0,{displaystyle k=n-1,n-2,ldots1,0,}
- ⋀ ⋀ nAn− − k=1n− − kTr ()A∘ ∘ ⋀ ⋀ n− − 1An− − k− − 1);{displaystyle {textstyle bigwedge } {n}A^{n-k}={frac} {1} {n-k}fnK} {Tr} (Acirc {textstyle bigwedge }{n-1}A^{n-k-1});}
- ⋀ ⋀ n− − 1An− − k=⋀ ⋀ nAn− − k⋅ ⋅ Id− − A∘ ∘ ⋀ ⋀ n− − 1An− − k− − 1.{displaystyle {textstyle bigwedge }{n-1}A^{n-k}={textstyle bigwedge {Id} -Acirc {style bigwedge } {n-1}A^{n-k-1}.}
Física
En física, muchas cantidades se representan naturalmente mediante operadores alternos. Por ejemplo, si el movimiento de una partícula cargada se describe mediante vectores de velocidad y aceleración en un espacio-tiempo de cuatro dimensiones, entonces la normalización del vector de velocidad requiere que la fuerza electromagnética sea un operador alterno en la velocidad. Sus seis grados de libertad se identifican con los campos eléctrico y magnético.
Geometría lineal
Los vectores k descomponibles tienen interpretaciones geométricas: el bivector u ∧ v representa el plano atravesado por los vectores, "ponderado" con un número, dado por el área del paralelogramo orientado de lados u y v. Análogamente, el vector de 3 u ∧ v ∧ w representa el espacio de 3 espacios ponderado por el volumen del paralelepípedo orientado con aristas u, v y w.
Geometría proyectiva
Descompuesto k-Véctores en ⋀ ⋀ kV{textstyle bigwedge nolimits ^{k}V} corresponde a ponderado k- subespacios lineales dimensionales de V. En particular, el Grassmanniano de k- subespacios dimensionales de V, Gr denotadok()V), se puede identificar naturalmente con una subvariedad algebraica del espacio proyector P()⋀ ⋀ kV).{textstyle P{bigl (}bigwedge nolimits ^{k}V{bigr)}.} Esto se llama la incrustación de Plücker.
Geometría diferencial
El álgebra exterior tiene aplicaciones notables en geometría diferencial, donde se utiliza para definir formas diferenciales. Las formas diferenciales son objetos matemáticos que evalúan la longitud de vectores, áreas de paralelogramos y volúmenes de cuerpos de dimensiones superiores, por lo que pueden integrarse en curvas, superficies y variedades de dimensiones superiores de una manera que generaliza las integrales de línea y las integrales de superficie del cálculo.. Una forma diferencial en un punto de una variedad diferenciable es una forma multilineal alterna en el espacio tangente en el punto. De manera equivalente, una forma diferencial de grado k es un funcional lineal en la potencia exterior k-ésima del espacio tangente. En consecuencia, el producto exterior de formas multilineales define un producto exterior natural para formas diferenciales. Las formas diferenciales juegan un papel importante en diversas áreas de la geometría diferencial.
Un enfoque alternativo define formas diferenciales en términos de gérmenes de funciones.
En particular, la derivada exterior le da al álgebra exterior de formas diferenciales en una variedad la estructura de un álgebra graduada diferencial. La derivada exterior conmuta con retroceso a lo largo de mapeos suaves entre variedades y, por lo tanto, es un operador diferencial natural. El álgebra exterior de formas diferenciales, equipada con la derivada exterior, es un complejo cocadenario cuya cohomología se denomina cohomología de Rham de la variedad subyacente y juega un papel vital en la topología algebraica de las variedades diferenciables.
Teoría de la representación
En la teoría de la representación, el álgebra exterior es uno de los dos funtores de Schur fundamentales en la categoría de espacios vectoriales, siendo el otro el álgebra simétrica. Juntas, estas construcciones se utilizan para generar las representaciones irreductibles del grupo lineal general; ver representación fundamental.
Superespacio
El álgebra exterior sobre los números complejos es el ejemplo arquetípico de una superálgebra, que juega un papel fundamental en las teorías físicas relativas a los fermiones y la supersimetría. Un solo elemento del álgebra exterior se llama supernúmero o número de Grassmann. El álgebra exterior en sí es entonces solo un superespacio unidimensional: es solo el conjunto de todos los puntos en el álgebra exterior. La topología en este espacio es esencialmente la topología débil, siendo los conjuntos abiertos los conjuntos de cilindros. Un superespacio de n-dimensional es solo el producto de n veces de álgebras exteriores.
Homología del álgebra de mentira
Sea L un álgebra de Lie sobre un campo K, entonces es posible definir la estructura de un complejo en cadena sobre el álgebra exterior de L. Este es un mapeo lineal K
- ∂ ∂ :⋀ ⋀ p+1L→ → ⋀ ⋀ pL{displaystyle partial:{textstyle bigwedge }^{p+1}Lto {textstyle bigwedge }^{p}L}
definido en elementos descomponibles por
- <math alttext="{displaystyle partial (x_{1}wedge cdots wedge x_{p+1})={frac {1}{p+1}}sum _{j∂ ∂ ()x1∧ ∧ ⋯ ⋯ ∧ ∧ xp+1)=1p+1.. j.l l ()− − 1)j+l l +1[xj,xl l ]∧ ∧ x1∧ ∧ ⋯ ⋯ ∧ ∧ x^ ^ j∧ ∧ ⋯ ⋯ ∧ ∧ x^ ^ l l ∧ ∧ ⋯ ⋯ ∧ ∧ xp+1.{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}<img alt="{displaystyle partial (x_{1}wedge cdots wedge x_{p+1})={frac {1}{p+1}}sum _{j
La identidad Jacobi tiene si y sólo si ♪ ♪♪, y por lo tanto esta es una condición necesaria y suficiente para un álgebra nonassociativa anticommutante L para ser un álgebra de Lie. Además, en ese caso ⋀ ⋀ L{textstyle bigwedge L} es un complejo de cadena con operador de límites. La homología asociada a este complejo es la homología del álgebra Lie.
Álgebra homológica
El álgebra exterior es el ingrediente principal en la construcción del complejo de Koszul, un objeto fundamental en el álgebra homológica.
Historia
El álgebra exterior fue introducido por primera vez por Hermann Grassmann en 1844 bajo el término general de Ausdehnungslehre, o Teoría de la Extensión. Esto se refería más generalmente a una teoría algebraica (o axiomática) de cantidades extendidas y fue uno de los primeros precursores de la noción moderna de un espacio vectorial. Saint-Venant también publicó ideas similares de cálculo exterior para las que reclamó prioridad sobre Grassmann.
El álgebra en sí se construyó a partir de un conjunto de reglas, o axiomas, que capturan los aspectos formales de la teoría de los multivectores de Cayley y Sylvester. Por tanto, era un cálculo, muy parecido al cálculo proposicional, excepto que se centraba exclusivamente en la tarea del razonamiento formal en términos geométricos. En particular, este nuevo desarrollo permitió una caracterización axiomática de la dimensión, una propiedad que anteriormente solo había sido examinada desde el punto de vista de las coordenadas.
La importancia de esta nueva teoría de vectores y multivectores se perdió para los matemáticos de mediados del siglo XIX, hasta que Giuseppe Peano lo revisó a fondo en 1888. El trabajo de Peano también permaneció algo oscuro hasta el cambio de siglo, cuando el tema fue unificado por miembros de la escuela de geometría francesa (en particular, Henri Poincaré, Élie Cartan y Gaston Darboux).) quien aplicó las ideas de Grassmann al cálculo de formas diferenciales.
Poco tiempo después, Alfred North Whitehead, tomando prestadas las ideas de Peano y Grassmann, presentó su álgebra universal. Esto allanó el camino para los desarrollos del álgebra abstracta del siglo XX al colocar la noción axiomática de un sistema algebraico sobre una base lógica firme.
Contenido relacionado
Topología de Grothendieck
Theodore von Karmán
Independencia (teoría de la probabilidad)





























![{displaystyle F_{ij}=A_{[i,j]}=A_{[i;j]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4158dbf3e9425d402c1c7350c68a73ac96a0176f)

![{displaystyle F_{[ij,k]}=F_{[ij;k]}=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39498c21115979961e612d1ea550016064bc6659)


















































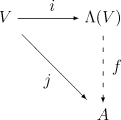









![{displaystyle (t~{widehat {otimes }}~s)^{i_{1}cdots i_{r+p}}=t^{[i_{1}cdots i_{r}}s^{i_{r+1}cdots i_{r+p}]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3a6e1f0d329e0d2883efe13d67dc45065142bba)





































































































































