Álgebra elemental

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Conceptos básicos del álgebra

{displaystyle {overset {}{underset {}{x={frac {-bpm {sqrt {b^{2}-4ac}}}{2a}}}}}}

La fórmula cuadrática, que es la solución a la ecuación cuadrática

ax^2+bx+c=0

Donde

{displaystyle aneq 0}

. Aquí los símbolos

a

b

, y

c

representan números arbitrarios, y

x

es una variable que representa la solución de la ecuación.

Parcela bidimensional (curva roja) de la ecuación algebraica

y = x^2 - x - 2

Álgebra elemental engloba los conceptos básicos del álgebra. A menudo se contrasta con la aritmética: la aritmética trata con números específicos, mientras que el álgebra introduce variables (cantidades sin valores fijos).

Este uso de variables implica el uso de la notación algebraica y la comprensión de las reglas generales de las operaciones introducidas en la aritmética. A diferencia del álgebra abstracta, el álgebra elemental no se ocupa de las estructuras algebraicas fuera del ámbito de los números reales y complejos.

Por lo general, se enseña a estudiantes de secundaria y se basa en su comprensión de la aritmética. El uso de variables para denotar cantidades permite que las relaciones generales entre cantidades se expresen de manera formal y concisa y, por lo tanto, permite resolver una gama más amplia de problemas. Muchas relaciones cuantitativas en ciencias y matemáticas se expresan como ecuaciones algebraicas.

Notación algebraica

La notación algebraica describe las reglas y convenciones para escribir expresiones matemáticas, así como la terminología utilizada para hablar de partes de expresiones. Por ejemplo, la expresión $3x^{2}-2xy+c$ tiene los siguientes componentes:

exponente (poder)
coeficiente
mandato
operación
constante,
$x, y$ . variables

A coeficiente es un valor numérico, o letra que representa una constante numérica, que multiplica una variable (el operador es omitido). A mandato es un addend o un summand, un grupo de coeficientes, variables, constantes y exponentes que pueden ser separados de los otros términos por los operadores más y menos. Las cartas representan variables y constantes. Por convención, letras al principio del alfabeto (por ejemplo, $a,b,c$ ) se utilizan típicamente para representar constantes, y los hacia el final del alfabeto (por ejemplo. $x,y$ y $z$ ) se utilizan para representar variables. Por lo general están impresos en cursiva.

Las operaciones algebraicas funcionan de la misma manera que las operaciones aritméticas, tales como adición, resta, multiplicación, división y exponentiación. y se aplican a variables y términos algebraicos. Los símbolos multiplicación se omiten generalmente, e implican cuando no hay espacio entre dos variables o términos, o cuando se utiliza un coeficiente. Por ejemplo, $3 times x^2$ está escrito como $3x^2$ , y $2 times x times y$ puede ser escrito $2xy$ .

Por lo general, los términos con mayor potencia (exponente), se escriben a la izquierda, por ejemplo, $x^{2}$ está escrito a la izquierda $x$ . Cuando un coeficiente es uno, generalmente se omite (por ejemplo. $1x^{2}$ escrito $x^{2}$ ). Del mismo modo cuando el exponente (poder) es uno (por ejemplo, $3x^{1}$ escrito $3x$ ). Cuando el exponente es cero, el resultado es siempre 1 (por ejemplo. $x^{0}$ es siempre reescrito $1$ ). Sin embargo $0^{0}$ , siendo indefinido, no debe aparecer en una expresión, y se debe tener cuidado en simplificar expresiones en las que las variables pueden aparecer en exponentes.

Notación alternativa

Otros tipos de notación se utilizan en expresiones algebraicas cuando el formato requerido no está disponible, o no puede ser implícito, como donde sólo letras y símbolos están disponibles. Como ilustración de esto, mientras que los exponentes generalmente se formatean utilizando superscripts, por ejemplo, $x^{2}$ , en texto llano, y en el lenguaje TeX marcado, el símbolo cuidado ^ representa la exponenciación, así $x^{2}$ está escrito como "x^2", así como algunos lenguajes de programación como Lua. En lenguajes de programación como Ada, Fortran, Perl, Python y Ruby, se utiliza un doble asterisco, por lo que $x^{2}$ está escrito como "x**2". Muchos lenguajes de programación y calculadoras utilizan un solo asterisco para representar el símbolo de multiplicación, y debe ser utilizado explícitamente, por ejemplo, $3x$ está escrito "3*x".

Conceptos

Variables

Ejemplo de variables que muestran la relación entre el diámetro de un círculo y su circunferencia. Para cualquier círculo, su circunferencia

c

, dividido por su diámetro

d

, es igual a la pi constante,

pi

(aproximadamente 3.14).

El álgebra elemental se basa en la aritmética y la amplía mediante la introducción de letras llamadas variables para representar números generales (no especificados). Esto es útil por varias razones.

Las variables pueden representar números cuyos valores aún no se conocen. Por ejemplo, si la temperatura del día actual, C, es 20 grados más alta que la temperatura del día anterior, P, entonces el problema se puede describir algebraicamente como ${displaystyle C=P+20}$ .
Variables permiten describir general problemas, sin especificar los valores de las cantidades involucradas. Por ejemplo, se puede decir específicamente que 5 minutos equivalen a $60 times 5 = 300$ segundos. Una descripción más general (algebraica) puede indicar que el número de segundos, $s = 60 times m$ , donde m es el número de minutos.
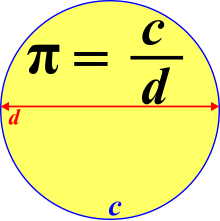
Las variables permiten describir relaciones matemáticas entre cantidades que pueden variar. Por ejemplo, la relación entre la circunferencia, c, y diámetro, d, de un círculo se describe por $pi = c /d$ .
Las variables permiten describir algunas propiedades matemáticas. Por ejemplo, una propiedad básica de la adición es la conmutación que establece que el orden de los números que se agregan juntos no importa. Commutatividad se declara algebraicamente como $(a + b) = (b + a)$ .

Simplificar expresiones

Las expresiones algebraicas pueden evaluarse y simplificarse en función de las propiedades básicas de las operaciones aritméticas (suma, resta, multiplicación, división y exponenciación). Por ejemplo,

Los términos adicionales se simplifican utilizando coeficientes. Por ejemplo, $x + x + x$ puede ser simplificado como $3x$ (donde 3 es un coeficiente numérico).
Los términos multiplicados se simplifican utilizando exponentes. Por ejemplo, $x times x times x$ está representado $x^{3}$
Como los términos se agregan juntos, por ejemplo, $2x^2 + 3ab - x^2 + ab$ está escrito como $x^2 + 4ab$ , porque los términos que contienen $x^{2}$ se agregan juntos, y, los términos que contienen $ab$ se añaden juntos.
Los frenos pueden ser "multiplidos", utilizando la propiedad distributiva. Por ejemplo, $x (2x + 3)$ puede ser escrito como $(x times 2x) + (x times 3)$ que puede ser escrito como $2x^2 + 3x$
Se pueden tener en cuenta las expresiones. Por ejemplo, $6x^5 + 3x^2$ , dividiendo ambos términos por $3x^2$ puede ser escrito como $3x^2 (2x^3 + 1)$

Ecuaciones

Animación que ilustra la regla de Pitágoras para un triángulo recto-ángulo, que muestra la relación algebraica entre la hipotenusa del triángulo, y los otros dos lados.

Una ecuación establece que dos expresiones son iguales usando el símbolo de igualdad, = (el signo igual). Una de las ecuaciones más conocidas describe Pitágoras' Ley que relaciona la longitud de los lados de un triángulo rectángulo:

c^2 = a^2 + b^2

Esta ecuación declara que $c^{2}$ , representando el cuadrado de la longitud del lado que es el hipotenusa, el lado opuesto al ángulo recto, es igual a la suma (addición) de los cuadrados de los otros dos lados cuyas longitudes están representadas por $a$ y $b$ .

Una ecuación es la afirmación de que dos expresiones tienen el mismo valor y son iguales. Algunas ecuaciones son verdaderas para todos los valores de las variables involucradas (como $a + b = b + a$ ); tales ecuaciones se llaman identidades. Las ecuaciones condicionales son verdaderas sólo para algunos valores de las variables implicadas, por ejemplo. $x^2 - 1 = 8$ es verdad sólo $x = 3$ y $x = -3$ . Los valores de las variables que hacen realidad la ecuación son las soluciones de la ecuación y se pueden encontrar a través de la resolución de la ecuación.

Otro tipo de ecuación es la desigualdad. Las desigualdades se utilizan para demostrar que un lado de la ecuación es mayor, o menos, que el otro. Los símbolos utilizados para esto son: $b}" xmlns="http://www.w3.org/1998/Math/MathML">a■b{displaystyle a prendab} b " aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/83fc0063781fb9bf4ec7608b2fd11ed6d5b05a13" style="vertical-align: -0.338ex; width:5.326ex; height:2.176ex;"/>$ Donde $}" xmlns="http://www.w3.org/1998/Math/MathML">■{displaystyle } " aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1b27b77ab4e3293ea9ce65cef60fea655c398423" style="vertical-align: -0.338ex; width:1.808ex; height:1.843ex;"/>$ representa 'más grande que', y $<math alttext="{displaystyle a a.b{displaystyle a meantb} <img alt=" a$ Donde $<math alttext="{displaystyle .{displaystyle] <img alt="$ representa 'menos que'. Al igual que las ecuaciones estándar de igualdad, los números se pueden añadir, restar, multiplicar o dividir. La única excepción es que cuando se multiplica o se divide por un número negativo, el símbolo de desigualdad debe ser volteado.

Propiedades de la igualdad

Por definición, la igualdad es una relación de equivalencia, lo que significa que tiene las propiedades (a) reflexivas (es decir. $b = b$ ), (b) simétrico (es decir, si $a=b$ entonces $b=a$ c) transitivo (es decir, si $a=b$ y $b=c$ entonces $a=c$ ). También satisface la propiedad importante que si dos símbolos se utilizan para las cosas iguales, entonces un símbolo puede ser sustituido por el otro en cualquier declaración verdadera sobre el primero y la declaración seguirá siendo verdad. Esto implica las siguientes propiedades:

si $a=b$ y $c = d$ entonces $a + c = b + d$ y $ac = bd$ ;
si $a=b$ entonces $a + c = b + c$ y ${displaystyle ac=bc}$ ;
más generalmente, para cualquier función $f$ , si $a=b$ entonces $f(a) = f(b)$ .

Propiedades de la desigualdad

Las relaciones menos que $<math alttext="{displaystyle .{displaystyle] <img alt="$ más grande que $}" xmlns="http://www.w3.org/1998/Math/MathML">■{displaystyle } " aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1b27b77ab4e3293ea9ce65cef60fea655c398423" style="vertical-align: -0.338ex; width:1.808ex; height:1.843ex;"/>$ tienen la propiedad de la transitividad:

Si $<math alttext="{displaystyle a a.b{displaystyle a meantb} <img alt="a$ y $<math alttext="{displaystyle bb.c{displaystyle b) <img alt="b$ entonces $<math alttext="{displaystyle aa.c{displaystyle aludec} <img alt="a$ ;
Si $<math alttext="{displaystyle a a.b{displaystyle a meantb} <img alt="a$ y $<math alttext="{displaystyle cc.d{displaystyle c realizadas} <img alt="c$ entonces $<math alttext="{displaystyle a+c a+c.b+d{displaystyle a+ccantab+d} <img alt="a + c$ ;
Si $<math alttext="{displaystyle a a.b{displaystyle a meantb} <img alt="a$ y $0}" xmlns="http://www.w3.org/1998/Math/MathML">c■0{displaystyle c]0}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/2ba126f626d61752f62eaacaf11761a54de4dc84" style="vertical-align: -0.338ex; width:5.268ex; height:2.176ex;"/>$ entonces $<math alttext="{displaystyle acac.bc{displaystyle ac\cdotbc} <img alt="ac$ ;
Si $<math alttext="{displaystyle a a.b{displaystyle a meantb} <img alt="a$ y $<math alttext="{displaystyle cc.0{displaystyle c realizadas0} <img alt="c$ entonces $<math alttext="{displaystyle bcbc.ac{displaystyle bc madeac} <img alt="bc$ .

Al invertir la inecuencia, $<math alttext="{displaystyle .{displaystyle] <img alt="$ y $}" xmlns="http://www.w3.org/1998/Math/MathML">■{displaystyle } " aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1b27b77ab4e3293ea9ce65cef60fea655c398423" style="vertical-align: -0.338ex; width:1.808ex; height:1.843ex;"/>$ se puede cambiar, por ejemplo:

$<math alttext="{displaystyle a a.b{displaystyle a meantb} <img alt="a$ equivale a $a}" xmlns="http://www.w3.org/1998/Math/MathML">b■a{displaystyle b confíaa}a" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/5b1cfc86ca957eea4f09d683db2412a173f6f404" style="vertical-align: -0.338ex; width:5.326ex; height:2.176ex;"/>$

Sustitución

La sustitución reemplaza los términos en una expresión para crear una nueva expresión. Sustitución 3 $a$ en la expresión $a *5$ hace una nueva expresión $3*5$ con significado $15$ . La sustitución de los términos de una declaración hace una nueva declaración. Cuando la declaración original es verdadera independientemente de los valores de los términos, la declaración creada por las sustituciones es también verdadera. Por lo tanto, las definiciones pueden hacerse en términos simbólicos e interpretarse mediante la sustitución: si ${displaystyle a^{2}:=atimes a}$ se entiende como la definición ${displaystyle a^{2},}$ como el producto de $a$ con él mismo, sustitución $3$ para $a$ informa al lector de esta declaración que $3^2$ medios $3 \times 3 = 9$ . A menudo no se sabe si la declaración es verdadera independientemente de los valores de los términos. Y, la sustitución permite a uno derivar restricciones a los posibles valores, o mostrar en qué condiciones se encuentra la declaración. Por ejemplo, tomando la declaración $x + 1 = 0$ , si $x$ se sustituye con $1$ , esto implica $1 + 1 = 2 = 0$ , que es falso, lo que implica que $x + 1 = 0$ entonces $x$ no puede ser $1$ .

Si $x$ y $y$ son números enteros, racionales, o números reales, entonces $xy = 0$ implica $x = 0$ o $y = 0$ . Considere $abc = 0$ . Luego, sustituyendo $a$ por $x$ y $bc$ para $y$ , aprendemos $a = 0$ o $bc = 0$ . Entonces podemos sustituir de nuevo, dejando $x = b$ y $y = c$ , para mostrar que si $bc = 0$ entonces $b = 0$ o $c = 0$ . Por lo tanto, si $abc = 0$ , entonces $a = 0$ o ( $b = 0$ o $c = 0$ ), entonces $abc = 0$ implica $a = 0$ o $b = 0$ o $c = 0$ .

Si el hecho original se estableciera como " $ab = 0$ implica $a = 0$ o $b = 0$ ", luego al decir "considere abc = 0," tendríamos un conflicto de términos al sustituir. Sin embargo, la lógica anterior sigue siendo válida para mostrar que si $abc = 0$ entonces $a = 0$ o $b = 0$ o $c = 0$ si, en lugar de dejar $a = a$ y $b = bc$ , uno sustituye $a$ por $a$ y $b$ para $bc$ (y con $bc = 0$ , sustituyendo $b$ por $a$ y $c$ para $b$ ). Esto muestra que sustituir los términos en un enunciado no siempre es lo mismo que dejar que los términos del enunciado sean iguales a los términos sustituidos. En esta situación, está claro que si sustituimos una expresión $a$ en $a$ término de la ecuación original, el $a$ sustituido no se refiere al $a$ en la sentencia " $ab = 0$ implica $a = 0$ o $b = 0$ ."

Resolver ecuaciones algebraicas

Un problema típico de álgebra.

Las siguientes secciones presentan ejemplos de algunos de los tipos de ecuaciones algebraicas que se pueden encontrar.

Ecuaciones lineales con una variable

Las ecuaciones lineales se llaman así porque cuando se trazan, describen una línea recta. Las ecuaciones más sencillas de resolver son las ecuaciones lineales que tienen una sola variable. Contienen solo números constantes y una sola variable sin exponente. Como ejemplo, considere:

Problema en palabras: Si duplicas la edad de un niño y añades 4, la respuesta resultante es 12. ¿Cuántos años tiene el niño?

Ecuación equivalente: $2x + 4 = 12$ Donde $x$ representar la edad del niño

Para resolver este tipo de ecuaciones, la técnica es sumar, restar, multiplicar o dividir ambos lados de la ecuación por el mismo número para aislar la variable en un lado de la ecuación. Una vez aislada la variable, el otro lado de la ecuación es el valor de la variable. Este problema y su solución son los siguientes:

Resolver para x

1. Ecuación para resolver:	$2x + 4 = 12$
2. Apartado 4 de ambas partes:	$2x + 4 - 4 = 12 - 4$
3. Esto simplifica:	$2x = 8$
4. Divide ambos lados por 2:	$frac{2x}{2} = frac{8}{2}$
5. Esto simplifica la solución:	$x = 4$

En palabras: el niño tiene 4 años.

La forma general de una ecuación lineal con una variable, se puede escribir como: ${displaystyle ax+b=c}$

Siguiendo el mismo procedimiento (es decir, subtracto $b$ de ambos lados, y luego dividir por $a$ ), la solución general es dada por $x=frac{c-b}{a}$

Ecuaciones lineales con dos variables

Resolver dos ecuaciones lineales con una solución única en el punto que se intersectan.

Una ecuación lineal con dos variables tiene muchas (es decir, un número infinito de) soluciones. Por ejemplo:

Problema en palabras: Un padre tiene 22 años más que su hijo. ¿Cuántos años tienen?

Ecuación equivalente: $y = x + 22$ Donde $Sí.$ es la edad del padre, $x$ es la edad del hijo.

Eso no se puede resolver por sí solo. Si se supiera la edad del hijo, ya no habría dos incógnitas (variables). El problema entonces se convierte en una ecuación lineal con una sola variable, que se puede resolver como se describe arriba.

Para resolver una ecuación lineal con dos variables (incógnitas), se requieren dos ecuaciones relacionadas. Por ejemplo, si también se revelara que:

Problema en palabras: En 10 años, el padre tendrá el doble de edad que su hijo.
Ecuación equivalente: ${displaystyle {begin{aligned}y+10&=2times (x+10)\y&=2times (x+10)-10&&{text{Subtract 10 from both sides}}\y&=2x+20-10&&{text{Multiple out brackets}}\y&=2x+10&&{text{Simplify}}end{aligned}}}$

Ahora hay dos ecuaciones lineales relacionadas, cada una con dos incógnitas, lo que permite producir una ecuación lineal con una sola variable, restando una de la otra (llamado método de eliminación):

${displaystyle {begin{cases}y=x+22&{text{First equation}}\y=2x+10&{text{Second equation}}end{cases}}}$

${displaystyle {begin{aligned}&&&{text{Subtract the first equation from}}\(y-y)&=(2x-x)+10-22&&{text{the second in order to remove }}y\0&=x-12&&{text{Simplify}}\12&=x&&{text{Add 12 to both sides}}\x&=12&&{text{Rearrange}}end{aligned}}}$

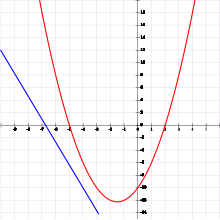
En otras palabras, el hijo tiene 12 años, y como el padre es 22 años mayor, debe tener 34. En 10 años, el hijo tendrá 22 y el padre tendrá el doble de su edad, 44. Este problema es ilustrado en la gráfica asociada de las ecuaciones.

Para conocer otras formas de resolver este tipo de ecuaciones, consulte a continuación, Sistema de ecuaciones lineales.

Ecuaciones cuadráticas

Parcela de ecuación cuadrática $y = x^2 + 3x - 10$ mostrando sus raíces $x = -5$ y $x = 2$ , y que el cuadrático puede ser reescrito como $y = (x + 5)(x - 2)$

Una ecuación cuadrática es una que incluye un término con un exponente de 2, por ejemplo, $x^{2}$ , y ningún término con mayor exponente. El nombre deriva del latín quadrusSignifica cuadrado. En general, una ecuación cuadrática se puede expresar en la forma $ax^{2}+bx+c=0$ , donde $a$ no es cero (si fuera cero, entonces la ecuación no sería cuadratica sino lineal). Debido a esto una ecuación cuadrática debe contener el término $ax^2$ , que se conoce como el término cuadrático. Por lo tanto $aneq 0$ , y así podemos dividirnos $a$ y reorganizar la ecuación en la forma estándar

${displaystyle x^{2}+px+q=0}$

Donde ${displaystyle p={frac {b}{a}}}$ y ${displaystyle q={frac {c}{a}}}$ . Resolver esto, mediante un proceso conocido como completar la plaza, conduce a la fórmula cuadrática

$x=frac{-b pm sqrt {b^2-4ac}}{2a},$

donde el símbolo "±" indica que ambos

$x={frac {-b+{sqrt {b^{2}-4ac}}}{2a}}quad {text{and}}quad x={frac {-b-{sqrt {b^{2}-4ac}}}{2a}}$

son soluciones de la ecuación cuadrática.

Las ecuaciones cuadráticas también se pueden resolver usando factorización (cuyo proceso inverso es la expansión, pero para dos términos lineales a veces se denota frustración). Como ejemplo de factorización:

${displaystyle x^{2}+3x-10=0,}$

que es lo mismo que

${displaystyle (x+5)(x-2)=0.}$

Se deriva de la propiedad cero-producto que o $x = 2$ o $x = -5$ son las soluciones, ya que precisamente uno de los factores debe ser igual a cero. Todas las ecuaciones cuadráticas tendrán dos soluciones en el complejo sistema de números, pero no necesitan ninguna en el sistema de números reales. Por ejemplo,

${displaystyle x^{2}+1=0}$

no tiene solución de número real ya que ningún número real al cuadrado es igual a −1. A veces, una ecuación cuadrática tiene una raíz de multiplicidad 2, como:

${displaystyle (x+1)^{2}=0.}$

Para esta ecuación, −1 es una raíz de multiplicidad 2. Esto significa que −1 aparece dos veces, ya que la ecuación se puede reescribir en forma factorizada como

$[x-(-1)][x-(-1)]=0.$

Números complejos

Todas las ecuaciones cuadráticas tienen exactamente dos soluciones en números complejos (pero pueden ser iguales entre sí), una categoría que incluye números reales, números imaginarios y sumas de números reales e imaginarios. Los números complejos surgen por primera vez en la enseñanza de las ecuaciones cuadráticas y la fórmula cuadrática. Por ejemplo, la ecuación cuadrática

$x^{2}+x+1=0$

tiene soluciones

$x={frac {-1+{sqrt {-3}}}{2}}quad quad {text{and}}quad quad x={frac {-1-{sqrt {-3}}}{2}}.$

Desde ${sqrt {-3}}$ no es ningún número real, ambas soluciones para x son números complejos.

Ecuaciones exponenciales y logarítmicas

El gráfico del logaritmo a base 2 cruza el eje x (eje horizontal) a 1 y pasa a través de los puntos con coordenadas (2, 1), (4, 2), y (8, 3). Por ejemplo, log₂(8) = 3, porque 2³ = 8. El gráfico se acerca arbitrariamente al Sí. axis, pero no lo conoce o lo intersecciona.

Una ecuación exponencial es una que tiene la forma $a^x = b$ para $0}" xmlns="http://www.w3.org/1998/Math/MathML">a■0{displaystyle a confía0}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1f34a80ea013edb56e340b19550430a8b6dfd7b9" style="vertical-align: -0.338ex; width:5.491ex; height:2.176ex;"/>$ , que tiene solución

$X = log_a b = frac{ln b}{ln a}$

cuando $0}" xmlns="http://www.w3.org/1998/Math/MathML">b■0{displaystyle b confía0} 0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/94436473a90bd55191a79c59474cb5456dcbec00" style="vertical-align: -0.338ex; width:5.258ex; height:2.176ex;"/>$ . Las técnicas algebraicas elementales se utilizan para reescribir una ecuación dada de la manera anterior antes de llegar a la solución. Por ejemplo, si

$3 cdot 2^{x - 1} + 1 = 10$

entonces, restando 1 de ambos lados de la ecuación y luego dividiendo ambos lados por 3 obtenemos

${displaystyle 2^{x-1}=3}$

de donde

${displaystyle x-1=log _{2}3}$

${displaystyle x=log _{2}3+1.}$

Una ecuación logarítmica es una ecuación de la forma $log_a(x) = b$ para $0}" xmlns="http://www.w3.org/1998/Math/MathML">a■0{displaystyle a confía0}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1f34a80ea013edb56e340b19550430a8b6dfd7b9" style="vertical-align: -0.338ex; width:5.491ex; height:2.176ex;"/>$ , que tiene solución

${displaystyle X=a^{b}.}$

Por ejemplo, si

${displaystyle 4log _{5}(x-3)-2=6}$

entonces, al sumar 2 a ambos lados de la ecuación, seguido de dividir ambos lados por 4, obtenemos

${displaystyle log _{5}(x-3)=2}$

de donde

${displaystyle x-3=5^{2}=25}$

de donde obtenemos

${displaystyle x=28.}$

Ecuaciones radicales

${displaystyle {overset {}{underset {}{{sqrt[{2}]{x^{3}}}equiv x^{frac {3}{2}}}}}}$

Ecuación radical mostrando dos maneras de representar la misma expresión. La barra triple significa que la ecuación es verdadera para todos los valores x

Una ecuación radical es una que incluye un signo radical, que incluye raíces cuadradas, ${displaystyle {sqrt {x}},}$ raíces de cubo, ${sqrt[{3}]{x}}$ , y no raíces, ${sqrt[{n}]{x}}$ . Recuerda que un nla raíz puede ser reescrita en formato exponencial, de modo que ${sqrt[{n}]{x}}$ equivale a $x^{frac{1}{n}}$ . Combinado con exponentes regulares (poderes), entonces $sqrt[2]{x^3}$ (la raíz cuadrada de $x$ cubed), puede ser reescrito como $x^{frac{3}{2}}$ . Así que una forma común de una ecuación radical es ${sqrt[ {n}]{x^{m}}}=a$ (equivalente a $x^{{frac {m}{n}}}=a$ Donde $m$ y $n$ son enteros. Tiene una solución real:

$n$ Es extraño.	$n$ Incluso y $a ge 0$	$n$ y $m$ son incluso y $<math alttext="{displaystyle aa.0{displaystyle a won0} <img alt="a$	$n$ es incluso, $m$ Es extraño., y $<math alttext="{displaystyle aa.0{displaystyle a won0} <img alt="a$
${displaystyle x={sqrt[{n}]{a^{m}}}}$ equivalente ${displaystyle x=left({sqrt[{n}]{a}}right)^{m}}$	${displaystyle x=pm {sqrt[{n}]{a^{m}}}}$ equivalente ${displaystyle x=pm left({sqrt[{n}]{a}}right)^{m}}$	${displaystyle x=pm {sqrt[{n}]{a^{m}}}}$	ninguna solución real

Por ejemplo, si:

${displaystyle (x+5)^{2/3}=4}$

entonces

${displaystyle {begin{aligned}x+5&=pm ({sqrt {4}})^{3},\x+5&=pm 8,\x&=-5pm 8,end{aligned}}}$

y así

${displaystyle x=3quad {text{or}}quad x=-13}$

Sistema de ecuaciones lineales

Existen diferentes métodos para resolver un sistema de ecuaciones lineales con dos variables.

Método de eliminación

La solución para las ecuaciones $x - y = -1$ y $3x + y = 9$ es el único punto (2, 3).

Un ejemplo de cómo resolver un sistema de ecuaciones lineales es usando el método de eliminación:

${displaystyle {begin{cases}4x+2y&=14\2x-y&=1.end{cases}}}$

Multiplicando los términos de la segunda ecuación por 2:

${displaystyle 4x+2y=14}$

${displaystyle 4x-2y=2.}$

Sumar las dos ecuaciones para obtener:

${displaystyle 8x=16}$

que se simplifica a

${displaystyle x=2.}$

Desde el hecho de que $x = 2$ es conocido, entonces es posible deducir que $y = 3$ por cualquiera de las dos ecuaciones originales (utilizando 2 en lugar de $x$ ) La solución completa de este problema es entonces

${displaystyle {begin{cases}x=2\y=3.end{cases}}}$

Esta no es la única manera de resolver este sistema específico; $y$ podría haberse resuelto antes de $x.$

Método de sustitución

Otra forma de resolver el mismo sistema de ecuaciones lineales es por sustitución.

${displaystyle {begin{cases}4x+2y&=14\2x-y&=1.end{cases}}}$

Se puede deducir un equivalente para $y$ usando una de las dos ecuaciones. Usando la segunda ecuación:

${displaystyle 2x-y=1}$

Subtracting $2x$ de cada lado de la ecuación:

$begin{align}2x - 2x - y & = 1 - 2x \ - y & = 1 - 2x end{align}$

y multiplicando por −1:

${displaystyle y=2x-1.}$

Usando este valor $y$ en la primera ecuación del sistema original:

$begin{align}4x + 2(2x - 1) &= 14\ 4x + 4x - 2 &= 14 \ 8x - 2 &= 14 end{align}$

Sumar 2 en cada lado de la ecuación:

$begin{align}8x - 2 + 2 &= 14 + 2 \ 8x &= 16 end{align}$

que se simplifica a

${displaystyle x=2}$

Usando este valor en una de las ecuaciones, se obtiene la misma solución que en el método anterior.

${displaystyle {begin{cases}x=2\y=3.end{cases}}}$

Esta no es la única manera de resolver este sistema específico; en este caso también, $y$ podría haberse resuelto antes de que $x$ .

Otros tipos de sistemas de ecuaciones lineales

Sistemas inconsistentes

Las ecuaciones $3x + 2y = 6$ y $3x + 2y = 12$ son paralelos y no pueden interseccionar, y es insolvable.

Parcela de una ecuación cuadrática (rojo) y una ecuación lineal (azul) que no intersectan, y en consecuencia para la cual no hay solución común.

En el ejemplo anterior, existe una solución. Sin embargo, también existen sistemas de ecuaciones que no tienen solución. Tal sistema se llama inconsistente. Un ejemplo obvio es

$begin{cases}begin{align} x + y &= 1 \ 0x + 0y &= 2,. end{align} end{cases}$

Como 0≠2, la segunda ecuación del sistema no tiene solución. Por lo tanto, el sistema no tiene solución. Sin embargo, no todos los sistemas inconsistentes se reconocen a primera vista. Como ejemplo, considere el sistema

$begin{cases}begin{align}4x + 2y &= 12 \ -2x - y &= -4,. end{align}end{cases}$

Multiplicar por 2 ambos lados de la segunda ecuación y sumarla a la primera da como resultado

$0x+0y = 4 ,,$

que claramente no tiene solución.

Sistemas indeterminados

También hay sistemas que tienen infinitas soluciones, en contraste con un sistema con una solución única (es decir, un par único de valores para $x$ y $y$ ) Por ejemplo:

${displaystyle {begin{cases}{begin{aligned}4x+2y&=12\-2x-y&=-6end{aligned}}end{cases}}}$

Aislando $y$ en la segunda ecuación:

${displaystyle y=-2x+6}$

Y usando este valor en la primera ecuación del sistema:

$begin{align}4x + 2(-2x + 6) = 12 \ 4x - 4x + 12 = 12 \ 12 = 12 end{align}$

La igualdad es verdadera, pero no proporciona un valor $x$ . De hecho, uno puede verificar fácilmente (sólo llenando algunos valores de $x$ ) que para cualquier $x$ hay una solución mientras $y = -2x + 6$ . Hay un número infinito de soluciones para este sistema.

Sistemas sobre y subdeterminados

Los sistemas con más variables que el número de ecuaciones lineales se denominan subdeterminados. Tal sistema, si tiene alguna solución, no tiene una única sino una infinidad de ellas. Un ejemplo de tal sistema es

${begin{cases}{begin{aligned}x+2y&=10\y-z&=2.end{aligned}}end{cases}}$

Al tratar de resolverlo, uno se ve llevado a expresar algunas variables como funciones de las otras si existen soluciones, pero no puede expresar numéricamente todas las soluciones porque hay un número infinito de ellas si hay son cualquiera.

Un sistema con un mayor número de ecuaciones que de variables se denomina sobredeterminado. Si un sistema sobredeterminado tiene alguna solución, necesariamente algunas ecuaciones son combinaciones lineales de las otras.

Contenido relacionado

♯P
En la teoría de la complejidad computacional, la clase de complejidad #P es el conjunto de problemas de conteo asociados con los problemas de decisión en el...
Cono (desambiguación)
Un cono es una forma geométrica...
Sólida arquimediana(feminine)
En geometría, un sólido de Arquímedes es uno de los 13 sólidos enumerados por primera vez por Arquímedes. Son los poliedros uniformes convexos compuestos...
Más resultados...
Te puede interesar