Álgebra de Hopf

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Construcción en álgebra

En matemáticas, un álgebra de Hopf, llamada así por Heinz Hopf, es una estructura que es simultáneamente un álgebra (unital asociativa) y una coalgebra (coasociativa counitaria), con estas estructuras' compatibilidad haciéndola una biálgebra, y que además está dotada de un antiautomorfismo que satisface una cierta propiedad. La teoría de la representación de un álgebra de Hopf es particularmente agradable, ya que la existencia de comultiplicación, país y antípoda compatibles permite la construcción de productos tensoriales de representaciones, representaciones triviales y representaciones duales.

Los álgebras Hopf ocurren naturalmente en topología algebraica, donde se originaron y están relacionados con el concepto H-espacio, en teoría de esquemas de grupo, en teoría de grupo (a través del concepto de anillo de grupo), y en muchos otros lugares, haciéndolos probablemente el tipo más familiar de biálgebra. Los álgebras Hopf también son estudiados en su propio derecho, con mucho trabajo en clases específicas de ejemplos por un lado y problemas de clasificación por otro. Tienen diversas aplicaciones que van desde la física condensada y la teoría del campo cuántico hasta la teoría de cuerdas y la fenomenología de LHC.

Definición formal

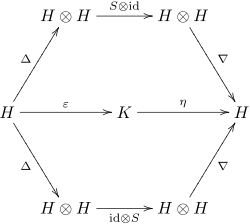
Formalmente, un álgebra de Hopf es una biálgebra (asociativa y coasociativa) H sobre un campo K junto con un mapa K-lineal S: H → H (llamada la antípoda) tal que el siguiente diagrama conmuta:

Aquí Δ es la comultiplicación de la biálgebra, ∇ su multiplicación, η su unidad y ε su counidad. En la notación de Sweedler sin suma, esta propiedad también se puede expresar como

{displaystyle S(c_{(1)})c_{(2)}=c_{(1)}S(c_{(2)})=varepsilon (c)1qquad {mbox{ for all }}cin H.}

En cuanto a las álgebras, se puede reemplazar el campo subyacente K con un anillo conmutativo R en la definición anterior.

La definición de álgebra de Hopf es autodual (como se refleja en la simetría del diagrama anterior), por lo que si se puede definir un dual de H (que siempre es posible si H es de dimensión finita), entonces es automáticamente un álgebra de Hopf.

Constantes de estructura

Fijación de una base ${displaystyle {e_{k}}}$ para el espacio vectorial subyacente, se puede definir el álgebra en términos de constantes de estructura para la multiplicación:

{displaystyle e_{i}nabla e_{j}=sum _{k}mu _{;ij}^{k}e_{k}}

para co-multiplicación:

{displaystyle Delta e_{i}=sum _{j,k}nu _{i}^{;jk}e_{j}otimes e_{k}}

y la antípoda:

{displaystyle Se_{i}=sum _{j}tau _{i}^{;j}e_{j}}

La asociatividad requiere entonces que

{displaystyle mu _{;ij}^{k}mu _{;kn}^{m}=mu _{;jn}^{k}mu _{;ik}^{m}}

mientras que la coasociación requiere que

{displaystyle nu _{k}^{;ij}nu _{i}^{;mn}=nu _{k}^{;mi}nu _{i}^{;nj}}

El axioma de conexión requiere que

{displaystyle nu _{k}^{;ij}tau _{j}^{;m}mu _{;pm}^{n}=nu _{k}^{;jm}tau _{j}^{,;i}mu _{;pm}^{n}}

Propiedades de la antípoda

A veces se requiere que la antípoda S tenga una inversa lineal K, que es automática en el caso de dimensión finita, o si H es conmutativo o coconmutativo (o más generalmente cuasitriangular).

Did you mean:

In general, S is an anti homomorphism, so S² is a homomorphism, which is therefore an isomorphism if S was invertible (as may be required).

Si S² = id_H, entonces se dice que el álgebra de Hopf es involutiva (y el álgebra subyacente con involución es un *-álgebra). Si H es semisimple de dimensión finita sobre un campo de característica cero, conmutativo o coconmutativo, entonces es involutivo.

Si una biálgebra B admite una antípoda S, entonces S es única ("una biálgebra admite como máximo 1 álgebra de Hopf estructura"). Así, la antípoda no plantea ninguna estructura extra que podamos elegir: Ser un álgebra de Hopf es una propiedad de una biálgebra.

La antípoda es un análogo al mapa de inversión en un grupo que envía g a g⁻¹.

Subálgebras de Hopf

Una subálgebra A de un álgebra de Hopf H es una subálgebra de Hopf si es una subcoálgebra de H y la antípoda S asigna A a A. En otras palabras, una subálgebra de Hopf A es un álgebra de Hopf por derecho propio cuando la multiplicación, comultiplicación, counidad y antípoda de H están restringidas a A (y además la identidad Se requiere que 1 de H esté en A). El teorema de libertad de Nichols-Zoeller estableció (en 1989) que el módulo natural A H está libre de rango finito si H es de dimensión finita: una generalización del teorema de Lagrange para subgrupos. Como corolario de esta teoría integral, una subálgebra de Hopf de un álgebra de Hopf de dimensión finita semisimple es automáticamente semisimple.

Se dice que una subálgebra de Hopf A es normal derecha en un álgebra de Hopf H si satisface la condición de estabilidad, ad_r(h)(A) ⊆ A para todas las h en H , donde el mapeo adjunto derecho ad_r está definido por ad_r(h )(a) = S(h₍₁₎)ah₍₂₎ para todo a en A, h en H. De manera similar, una subálgebra de Hopf A se deja normal en H si es estable bajo el mapeo adjunto izquierdo definido por ad_l(h)(a) = h₍₁₎aS(h₍₂₎). Las dos condiciones de normalidad son equivalentes si la antípoda S es biyectiva, en cuyo caso A se dice que es una subálgebra de Hopf normal.

Una subálgebra de Hopf normal A en H satisface la condición (de igualdad de subconjuntos de H): HA⁺ = A⁺H donde A⁺ denota el núcleo del país en A. Esta condición de normalidad implica que HA⁺ es un ideal de Hopf de H (es decir, un ideal de álgebra en el núcleo del país, un coideal de coalgebra y estable bajo las antípodas). Como consecuencia se tiene un cociente de álgebra de Hopf H/HA⁺ y epimorfismo H → H/A⁺H, una teoría análoga a la de los subgrupos normales y grupos cocientes en la teoría de grupos.

Órdenes Hopf

Un orden Hopf O sobre un dominio integral R con campo de fracciones K es un orden en un Álgebra de Hopf H sobre K que es cerrada bajo las operaciones de álgebra y coalgebra: en particular, la comultiplicación Δ asigna O a O⊗O.

Elementos similares a grupos

Un elemento similar a un grupo es un elemento distinto de cero x tal que Δ(x) = x⊗ x. Los elementos agrupados forman un grupo con inversa dada por la antípoda. Un elemento primitivo x satisface Δ(x) = x⊗1 + 1⊗x.

Ejemplos

	Dependiendo de	Comultiplicación	Counit	Antipode	Commutative	Cocommutative	Observaciones
grupo álgebra KG	grupo G	Δ(g) g ⊗ g para todos g dentro G	ε()g) = 1 para todos g dentro G	S()g) g⁻¹ para todos g dentro G	si G es abeliano	Sí.
funciones f de un grupo finito a K, K^G (con la adición y la multiplicación del punto)	grupo finito G	Δ(f)x,Sí.) f()xy)	ε()f) f(1_G)	S()f)x) f()x⁻¹)	Sí.	si G es abeliano
Funciones de representación en un grupo compacto	grupo compacto G	Δ(f)x,Sí.) f()xy)	ε()f) f(1_G)	S()f)x) f()x⁻¹)	Sí.	si G es abeliano	Por el contrario, cada álgebra de Hopf reducida conmutativamente C con un finito Haar integral surge de esta manera, dando una formulación de la dualidad Tannaka–Krein.
Funciones regulares en un grupo algebraico		Δ(f)x,Sí.) f()xy)	ε()f) f(1_G)	S()f)x) f()x⁻¹)	Sí.	si G es abeliano	Por el contrario, cada conmutación Álgebra de Hopf sobre un campo surge de un esquema de grupo de esta manera, dando una antiequivalencia de categorías.
Tensor álgebra T(V)	espacio vectorial V	Δ(x) x ⊗ 1 + 1 ⊗ x, x dentro V, Δ(1) = 1 ⊗ 1	ε()x) = 0	S()x) = −x para todos x en 'T¹()V) (y extendida a mayores poderes de tensor)	Si y sólo si dim(V)=0,1	Sí.	álgebra simétrica y álgebra exterior (que son cocientes del álgebra tensor) también son álgebras Hopf con esta definición de la comultiplicación, counidad y antipodo
Álgebra universal envolvente U(g)	Lie algebra g	Δ(x) x ⊗ 1 + 1 ⊗ x para todos x dentro g (esta regla es compatible con los conmutadores y por lo tanto puede extenderse únicamente a todos los U)	ε()x) = 0 para todos x dentro g (de nuevo, extendido a U)	S()x) = −x	si g es abeliano	Sí.
Álgebra Hopf de Sweedler H=K[c, x]/c² = 1, x² = 0 y xc =cx.	K es un campo con características diferentes de 2	Δ(c) c ⊗ c, Δ(x) c ⊗ x + x ⊗ 1, Δ(1) = 1 ⊗ 1	ε()c) = 1 y ε()x) = 0	S()c) c⁻¹ = c y S()x) = −cx	no	no	El espacio vectorial subyacente es generado por {1, c, x, cx} y así tiene dimensión 4. Este es el ejemplo más pequeño de un álgebra Hopf que es tanto no-commutante como no-cocommutante.
anillo de funciones simétricas		en términos de funciones simétricas homogéneas completas h_k ()k ≥ 1): Δ(h_k) = 1 ⊗ h_k + h₁ ⊗ h_k−1 +... + h_k−1 ⊗ h₁ + h_k ⊗ 1.	ε()h_k) = 0	S()h_k) = (−1)^k e_k	Sí.	Sí.

Tenga en cuenta que las funciones en un grupo finito se pueden identificar con el anillo de grupo, aunque es más natural pensar que son duales: el anillo de grupo consta de sumas finitas de elementos y, por lo tanto, se empareja con funciones sobre el grupo evaluando la función sobre los elementos sumados.

Cohomología de los grupos de Lie

El álgebra de la cohomología (sobre un campo $K$ ) de un grupo de Lie $G$ es un álgebra Hopf: la multiplicación es proporcionada por el producto de la taza, y la comultiplicación

{displaystyle H^{*}(G,K)rightarrow H^{*}(Gtimes G,K)cong H^{*}(G,K)otimes H^{*}(G,K)}

por la multiplicación del grupo ${displaystyle Gtimes Gto G}$ . Esta observación fue en realidad una fuente de la noción de álgebra Hopf. Usando esta estructura, Hopf demostró un teorema de estructura para el álgebra de cohomología de grupos de Lie.

Theorem (Hopf) Vamos $A$ ser un álgebra de Hopf cocommutante de tamaño finito en un campo de características 0. Entonces... $A$ (como álgebra) es un álgebra exterior libre con generadores de grado extraño.

Grupos cuánticos y geometría no conmutativa

Todos los ejemplos anteriores son conmutativos (es decir, la multiplicación es conmutativa) o co-conmutativos (es decir, Δ = T ∘ Δ donde el mapa de torsión T: H ⊗ H → H ⊗ H está definido por T (x ⊗ y) = y ⊗ x). Otras álgebras de Hopf interesantes son ciertas "deformaciones" o "cuantizaciones" de los del ejemplo 3 que no son ni conmutativos ni co-conmutativos. Estas álgebras de Hopf a menudo se denominan grupos cuánticos, un término que hasta ahora solo se define vagamente. Son importantes en geometría no conmutativa, siendo la idea la siguiente: un grupo algebraico estándar está bien descrito por su álgebra de Hopf estándar de funciones regulares; entonces podemos pensar en la versión deformada de este álgebra de Hopf como una descripción de un cierto "no estándar" o "cuantificado" grupo algebraico (que no es un grupo algebraico en absoluto). Si bien no parece haber una forma directa de definir o manipular estos objetos no estándar, todavía se puede trabajar con sus álgebras de Hopf y, de hecho, uno los identifica con sus álgebras de Hopf. De ahí el nombre "grupo cuántico".

Teoría de la representación

Sea A un álgebra de Hopf, y sean M y N módulos A. Entonces, M ⊗ N es también un módulo A, con

a(motimes n):=Delta(a)(m otimes n)=(a_1otimes a_2)(motimes n)=(a_1 m otimes a_2 n)

para m ∈ M, n ∈ N y Δ(a) = (a₁, a₂). Además, podemos definir la representación trivial como el campo base K con

a(m):=epsilon(a)m

para m ∈ K. Finalmente, se puede definir la representación dual de A: si M es un módulo A y M* es su espacio dual, entonces

(af)(m):=f(S(a)m)

donde f ∈ M* y m ∈ M.

La relación entre Δ, ε y S asegura que ciertos homomorfismos naturales de espacios vectoriales sean de hecho homomorfismos de módulos A. Por ejemplo, los isomorfismos naturales de los espacios vectoriales M → M ⊗ K y M → K ⊗ M también son isomorfismos de módulos A. Además, el mapa de espacios vectoriales M* ⊗ M → K con f ⊗ m → f(m) también es un homomorfismo de módulos A. Sin embargo, el mapa M ⊗ M* → K no es necesariamente un homomorfismo de módulos A.

Conceptos relacionados

Las álgebras de Hopf graduadas se utilizan a menudo en la topología algebraica: son la estructura algebraica natural de la suma directa de todos los grupos de homología o cohomología de un espacio H.

Los grupos cuánticos localmente compactos generalizan álgebras de Hopf y llevan una topología. El álgebra de todas las funciones continuas en un grupo de Lie es un grupo cuántico localmente compacto.

Las álgebras de Quasi-Hopf son generalizaciones de las álgebras de Hopf, donde la coasociación solo se sostiene hasta cierto punto. Se han utilizado en el estudio de las ecuaciones de Knizhnik-Zamolodchikov.

Las álgebras de Hopf multiplicadoras introducidas por Alfons Van Daele en 1994 son generalizaciones de las álgebras de Hopf donde la comultiplicación de un álgebra (con o sin unidad) al álgebra multiplicadora del álgebra de producto tensorial del álgebra consigo misma.

Las (co)álgebras de grupos de Hopf presentadas por V. G. Turaev en 2000 también son generalizaciones de las álgebras de Hopf.

Álgebras de Hopf débiles

Álgebras de Hopf débiles, o grupos cuánticos, son generalizaciones de álgebras de Hopf. Al igual que las álgebras de Hopf, las álgebras de Hopf débiles forman una clase de álgebras autodual; es decir, si H es un álgebra de Hopf (débil), también lo es H*, el espacio dual de formas lineales en H (con respecto a la estructura álgebra-coalgebra obtenida del emparejamiento natural con H y su estructura coalgebra-algebra). Un álgebra de Hopf débil H generalmente se toma como un

álgebra finito-dimensional y álgebra con coproducto Δ: H → H ⊗ H and counit ε: H → k satisfaciendo todos los axiomas de álgebra Hopf excepto posiblemente Δ(1) ≠ 1 o ε(ab) ε(a)ε(b) para algunos a,b dentro H. En cambio, se requiere lo siguiente:

(Delta(1) otimes 1)(1 otimes Delta(1)) = (1 otimes Delta(1))(Delta(1) otimes 1) = (Delta otimes mbox{Id})Delta(1)

epsilon(abc) = sum epsilon(ab_{(1)})epsilon(b_{(2)}c) = sum epsilon(ab_{(2)})epsilon(b_{(1)}c)

para todos a, b, y c dentro H.

H tiene un antipodo debilitado S: H → H satisfaciendo los axiomas:

$S(a_{(1)})a_{(2)} = 1_{(1)} epsilon(a 1_{(2)})$ para todos a dentro H (el lado derecho es la proyección interesante generalmente denotada por ^R()a) o ε_s()a) con la imagen un subalgebra separable denotado por H^R o H_s);
$a_{(1)}S(a_{(2)}) = epsilon(1_{(1)}a)1_{(2)}$ para todos a dentro H (Otra proyección interesante usualmente denotada por ■^R()a) o ε_t()a) con la imagen un álgebra separable H^L o H_t, antiisómorfo a H^L via S);
$S(a_{(1)})a_{(2)}S(a_{(3)}) = S(a)$ para todos a dentro H.

Tenga en cuenta que si Δ(1) = 1 ⊗ 1, estas condiciones reducen a las dos condiciones habituales en el antípodo de un álgebra Hopf.

Los axiomas se eligen en parte para que la categoría de los módulos H sea una categoría monoidal rígida. El módulo de unidad H es el álgebra separable H^L mencionado anteriormente.

Por ejemplo, un álgebra de grupoide finito es un álgebra de Hopf débil. En particular, el álgebra grupoide en [n] con un par de flechas invertibles e_ij y e_ji entre i y j en [n] es isomorfo al álgebra H de n matrices x n. La estructura del álgebra de Hopf débil en esta H particular viene dada por el coproducto Δ(e_ij) = e_ij ⊗ e_ij, país ε(e_ij) = 1 y antípoda S(e_ij) = e_ji. Las subálgebras separables H^L y H^R coinciden y son álgebras conmutativas no centrales en este caso particular (las subálgebra de matrices diagonales).

Las primeras contribuciones teóricas a las álgebras de Hopf débiles se encuentran tanto en

Algebroides de Hopf

Ver algebroide de Hopf

Analogía con grupos

Los grupos pueden ser axiomatizados por los mismos diagramas (equivalentemente, operaciones) como un álgebra de Hopf, donde G se toma como un conjunto en lugar de un módulo. En este caso:

sobre el terreno K es reemplazado por el conjunto de 1 punto
hay una counidad natural (mapa a 1 punto)
hay una comultiplicación natural (el mapa diagonal)
la unidad es el elemento de identidad del grupo
la multiplicación es la multiplicación en el grupo
el antípodo es el inverso

Did you mean:

In this philosophy, a group can be thought of as a Hopf algebra over the "field with one element#34;.

Álgebras de Hopf en categorías monoidales trenzadas

La definición de álgebra Hopf se extiende naturalmente a categorías monoidales trenzadas arbitrarias. A álgebra Hopf en tal categoría ${displaystyle (C,otimesI,alphalambdarhogamma)}$ es un sextuple ${displaystyle (H,nablaetaDeltavarepsilonS)}$ Donde $H$ es un objeto en $C$ , y

{displaystyle nabla:Hotimes Hto H}

(multiplicación),

{displaystyle eta:Ito H}

(unidad),

{displaystyle Delta:Hto Hotimes H}

(comultiplicación),

{displaystyle varepsilon:Hto I}

(counidad),

{displaystyle S:Hto H}

(antipode)

- son morfismos en $C$ tales que

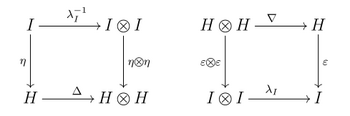
1) el triple

{displaystyle (H,nablaeta)}

es un monoide en la categoría monoidal

{displaystyle (C,otimesI,alphalambdarhogamma)}

, es decir, los siguientes diagramas son conmutativos:

2) el triple

{displaystyle (H,Deltavarepsilon)}

es comonoide en la categoría monoidal

{displaystyle (C,otimesI,alphalambdarhogamma)}

, es decir, los siguientes diagramas son conmutativos:

3) las estructuras de monoide y comonoide en

H

son compatibles: la multiplicación

nabla

y la unidad

eta

son morfismos de comonoides, y (esto es equivalente en esta situación) al mismo tiempo la comultiplicación

Delta

y la counidad

varepsilon

son morfismos de monoides; esto significa que los siguientes diagramas deben ser conmutativos:

Donde

{displaystyle lambda _{I}:Iotimes Ito I}

es el morfismo de la unidad izquierda

C

, y

theta

la transformación natural de los funerarios

{displaystyle (Aotimes B)otimes (Cotimes D){stackrel {theta }{rightarrowtail }}(Aotimes C)otimes (Botimes D)}

que es único en la clase de transformaciones naturales de functores compuestos de las transformaciones estructurales (asociatividad, unidades izquierdas y derechas, transposición y sus inversos) en la categoría

C

El quintuple ${displaystyle (H,nablaetaDeltavarepsilon)}$ con las propiedades 1),2),3) se llama a bialgebra en la categoría ${displaystyle (C,otimesI,alphalambdarhogamma)}$ ;

4) el diagrama de antipodo es conmutativo:

Los ejemplos típicos son los siguientes.

Grupos. En la categoría monoidal ${displaystyle ({text{Set}},times1)}$ de conjuntos (con el producto cartesiano $times$ como el producto tensor, y un singletone arbitrario, dicen, ${displaystyle 1={varnothing }}$ , como objeto de unidad) un triple ${displaystyle (H,nablaeta)}$ es un monoide en el sentido categórico si y sólo si es un monoide en el sentido algebraico habitual, es decir, si las operaciones ${displaystyle nabla (x,y)=xcdot y}$ y ${displaystyle eta (1)}$ comportarse como la multiplicación habitual y unidad en $H$ (pero posiblemente sin la invertibilidad de elementos $xin H$ ). Al mismo tiempo, un triple ${displaystyle (H,Deltavarepsilon)}$ es comonoide en el sentido categórico iff $Delta$ es la operación diagonal ${displaystyle Delta (x)=(x,x)}$ (y la operación $varepsilon$ se define de forma única también: ${displaystyle varepsilon (x)=varnothing }$ ). Y tal estructura de comonoide ${displaystyle (H,Deltavarepsilon)}$ es compatible con cualquier estructura de monoide ${displaystyle (H,nablaeta)}$ en el sentido de que los diagramas en la sección 3 de la definición siempre se comunican. Como corolario, cada monoide ${displaystyle (H,nablaeta)}$ dentro ${displaystyle ({text{Set}},times1)}$ puede ser considerado como un bialgebra ${displaystyle (H,nablaetaDeltavarepsilon)}$ dentro ${displaystyle ({text{Set}},times1)}$ , y viceversa. La existencia del antípodo ${displaystyle S:Hto H}$ para tal bialgebra ${displaystyle (H,nablaetaDeltavarepsilon)}$ significa exactamente que cada elemento $xin H$ tiene un elemento inverso ${displaystyle x^{-1}in H}$ con respecto a la multiplicación ${displaystyle nabla (x,y)=xcdot y}$ . Así, en la categoría de conjuntos ${displaystyle ({text{Set}},times1)}$ Los álgebras Hopf son exactamente grupos en el sentido algebraico habitual.
Álgebras clásicas de Hopf. En el caso especial cuando ${displaystyle (C,otimess,I)}$ es la categoría de espacios vectoriales sobre un campo dado $K$ , los álgebras Hopf en ${displaystyle (C,otimess,I)}$ son exactamente los álgebras Hopf clásicos descritos anteriormente.
Álgebras funcionales en grupos. Los álgebras funcionales estándar ${displaystyle {mathcal {C}}(G)}$ , ${displaystyle {mathcal {E}}(G)}$ , ${displaystyle {mathcal {O}}(G)}$ , ${displaystyle {mathcal {P}}(G)}$ (de funciones continuas, suaves, holomorfas y regulares) en grupos son álgebras Hopf en la categoría (Ste, $odot$ ) de espacios estereotipados,
Álgebras de grupo. El grupo estereotipo álgebras ${displaystyle {mathcal {C}}^{star }(G)}$ , ${displaystyle {mathcal {E}}^{star }(G)}$ , ${displaystyle {mathcal {O}}^{star }(G)}$ , ${displaystyle {mathcal {P}}^{star }(G)}$ (de medidas, distribuciones, funcionalidades analíticas y corrientes) en grupos son álgebras Hopf en la categoría (Ste, $circledast$ ) de espacios estereotipados. Estos álgebras Hopf se utilizan en las teorías de la dualidad para grupos no-commutantes.

Notas y referencias

Notas

Más resultados...