Álgebra

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

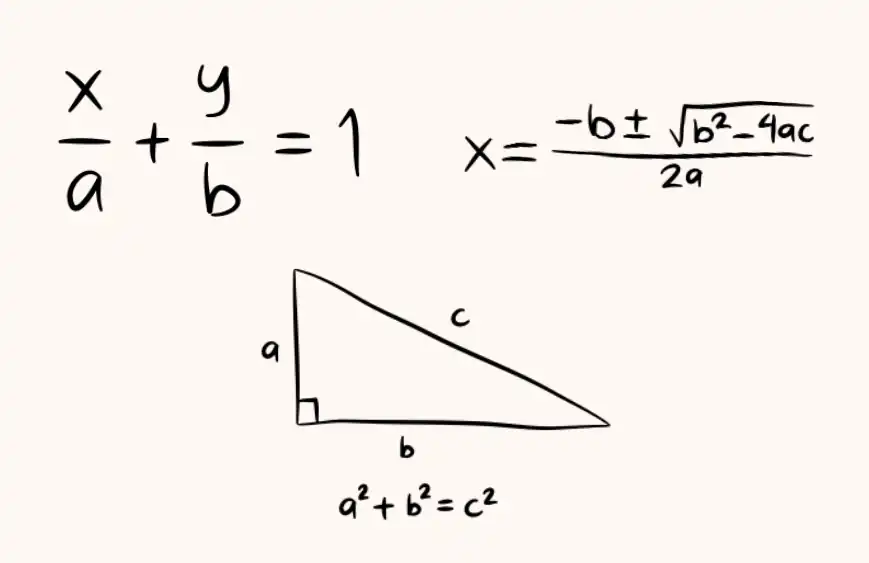
Álgebra (del árabe: الجبر, romanizado: al-jabr, lit. 'reunión de partes rotas, colocación de huesos ') es una de las áreas amplias de las matemáticas. En términos generales, el álgebra es el estudio de los símbolos matemáticos y las reglas para manipular estos símbolos; es un hilo unificador de casi todas las matemáticas.

El álgebra elemental se ocupa de la manipulación de variables como si fueran números, por lo que es fundamental en todas las aplicaciones de las matemáticas. Álgebra abstracta es el nombre que se le da en educación al estudio de estructuras algebraicas como grupos, anillos y campos. El álgebra lineal, que trata con ecuaciones lineales y mapeos lineales, se usa para presentaciones modernas de geometría y tiene muchas aplicaciones prácticas (en el pronóstico del tiempo, por ejemplo). Hay muchas áreas de las matemáticas que pertenecen al álgebra, algunas tienen "álgebra" en su nombre, como el álgebra conmutativa y otras no, como la teoría de Galois.

La palabra álgebra no solo se usa para nombrar un área de las matemáticas y algunas subáreas; también se usa para nombrar algunos tipos de estructuras algebraicas, como un álgebra sobre un campo, comúnmente llamada álgebra. A veces, la misma frase se usa para una subárea y sus principales estructuras algebraicas; por ejemplo, álgebra booleana y álgebra booleana. Un matemático especializado en álgebra se llama algebrista.

El álgebra como rama de las matemáticas

El álgebra comenzó con cálculos similares a los de la aritmética, con letras en lugar de números. Esto permitió pruebas de propiedades que son verdaderas sin importar qué números estén involucrados. Por ejemplo, en la ecuación cuadrática $hacha^{2}+bx+c=0,$

$a B C$ puede ser cualquier número (excepto que $a$ no puede ser ${ estilo de visualización 0}$ ), y la fórmula cuadrática se puede usar para encontrar rápida y fácilmente los valores de la cantidad desconocida $X$ que satisfacen la ecuación. Es decir, encontrar todas las soluciones de la ecuación.

Históricamente, y en la enseñanza actual, el estudio del álgebra comienza con la resolución de ecuaciones, como la ecuación cuadrática anterior. Luego, preguntas más generales, como "¿una ecuación tiene solución?", "¿cuántas soluciones tiene una ecuación?", "¿qué se puede decir sobre la naturaleza de las soluciones?" son considerados. Estas preguntas llevaron a extender el álgebra a objetos no numéricos, como permutaciones, vectores, matrices y polinomios. Las propiedades estructurales de estos objetos no numéricos luego se formalizaron en estructuras algebraicas como grupos, anillos y campos.

Antes del siglo XVI, las matemáticas se dividían en solo dos subcampos, la aritmética y la geometría. Si bien algunos métodos, que habían sido desarrollados mucho antes, pueden considerarse hoy como álgebra, la aparición del álgebra y, poco después, del cálculo infinitesimal como subcampos de las matemáticas solo data del siglo XVI o XVII. A partir de la segunda mitad del siglo XIX aparecieron muchos campos nuevos de las matemáticas, la mayoría de los cuales hacían uso tanto de la aritmética como de la geometría, y casi todos usaban el álgebra.

Hoy en día, el álgebra ha crecido considerablemente e incluye muchas ramas de las matemáticas, como se puede ver en la Clasificación de Materias Matemáticas donde ninguna de las áreas de primer nivel (entradas de dos dígitos) se denomina álgebra. Hoy álgebra incluye la sección 08-Sistemas algebraicos generales, 12-Teoría de campos y polinomios, 13-Álgebra conmutativa, 15-Álgebra lineal y multilineal; teoría de matrices, 16-Anillos y álgebras asociativas, 17-Anillos y álgebras no asociativas, 18-Teoría de categorías; álgebra homológica, teoría de 19-K y teoría de 20-Grupos. El álgebra también se usa ampliamente en la teoría de 11 números y la geometría de 14 algebraica.

Áreas de las matemáticas llamadas álgebra

Traducción de 1570 de Los Elementos de Euclides — Traducción de 1570 deLos Elementos de Euclides

Algunas subáreas de álgebra tienen la palabra álgebra en su nombre; el álgebra lineal es un ejemplo. Otros no: la teoría de grupos, la teoría de anillos y la teoría de campos son ejemplos. En esta sección, enumeramos algunas áreas de las matemáticas con la palabra "álgebra" en el nombre.

Álgebra elemental, la parte del álgebra que normalmente se enseña en los cursos elementales de matemáticas.
Álgebra abstracta, en la que se definen e investigan axiomáticamente estructuras algebraicas como grupos, anillos y campos.
Álgebra lineal, en la que se estudian las propiedades específicas de las ecuaciones lineales, los espacios vectoriales y las matrices.
Álgebra booleana, una rama del álgebra que abstrae el cálculo con los valores de verdad falso y verdadero.
Álgebra conmutativa, el estudio de los anillos conmutativos.
Álgebra informática, la implementación de métodos algebraicos como algoritmos y programas informáticos.
Álgebra homológica, el estudio de estructuras algebraicas que son fundamentales para estudiar espacios topológicos.
Álgebra universal, en la que se estudian propiedades comunes a todas las estructuras algebraicas.
Teoría algebraica de números, en la que se estudian las propiedades de los números desde un punto de vista algebraico.
Geometría algebraica, una rama de la geometría, en su forma primitiva que especifica curvas y superficies como soluciones de ecuaciones polinómicas.
Combinatoria algebraica, en la que se utilizan métodos algebraicos para estudiar cuestiones combinatorias.
Álgebra relacional: conjunto de relaciones finitas que se cierra bajo determinados operadores.

Muchas estructuras matemáticas se llaman álgebras:

Álgebra sobre un campo o, más generalmente, álgebra sobre un anillo.Muchas clases de álgebras sobre un campo o sobre un anillo tienen un nombre específico:
- Álgebra asociativa
- Álgebra no asociativa
- álgebra de mentira
- Álgebra de Hopf
- C*-álgebra
- álgebra simétrica
- álgebra exterior
- Álgebra tensorial
En la teoría de la medida,
- Sigma-álgebra
- Álgebra sobre un conjunto
En teoría de categorías
- F-álgebra y F-coálgebra
- T-álgebra
en lógica,
- Álgebra de relaciones, un álgebra booleana residual expandida con una involución llamada inversa.
- Álgebra booleana, un retículo distributivo complementado.
- Heyting álgebra

Álgebra elemental

El álgebra elemental es la forma más básica de álgebra. Se enseña a estudiantes que se supone que no tienen conocimientos de matemáticas más allá de los principios básicos de la aritmética. En aritmética, solo ocurren los números y sus operaciones aritméticas (como +, −, ×, ÷). En álgebra, los números a menudo se representan mediante símbolos llamados variables (como a, n, x, y o z). Esto es útil porque:

Permite la formulación general de leyes aritméticas (como a + b = b + a para todo a y b), y por lo tanto es el primer paso para una exploración sistemática de las propiedades del sistema de números reales.
Permite la referencia a números "desconocidos", la formulación de ecuaciones y el estudio de cómo resolverlas. (Por ejemplo, "Encuentra un número x tal que 3 x + 1 = 10" o yendo un poco más allá "Encuentra un número x tal que ax + b = c ". Este paso lleva a la conclusión de que no es la naturaleza de los números específicos que nos permiten resolverlo, sino el de las operaciones involucradas.)
Permite la formulación de relaciones funcionales. (Por ejemplo, "Si vende x boletos, su ganancia será de 3 x − 10 dólares, o f (x) = 3 x − 10, donde f es la función y x es el número al que se aplica la función ".)

Polinomios

Un polinomio es una expresión que es la suma de un número finito de términos distintos de cero, cada término consiste en el producto de una constante y un número finito de variables elevadas a potencias de números enteros. Por ejemplo, x + 2 x − 3 es un polinomio en la variable única x. Una expresión polinomial es una expresión que se puede reescribir como un polinomio mediante el uso de la conmutatividad, la asociatividad y la distributividad de la suma y la multiplicación. Por ejemplo, (x − 1)(x + 3) es una expresión polinomial que, propiamente hablando, no es un polinomio. Una función polinómica es una función definida por un polinomio o, de manera equivalente, por una expresión polinomial. Los dos ejemplos anteriores definen la misma función polinomial.

Dos problemas importantes y relacionados en álgebra son la factorización de polinomios, es decir, expresar un polinomio dado como un producto de otros polinomios que no se pueden factorizar más, y el cálculo de los máximos comunes divisores de polinomios. El polinomio de ejemplo anterior se puede factorizar como (x − 1)(x + 3). Una clase de problemas relacionados es encontrar expresiones algebraicas para las raíces de un polinomio en una sola variable.

Educación

Se ha sugerido que el álgebra elemental debería enseñarse a estudiantes a partir de los once años, aunque en los últimos años es más común que las lecciones públicas comiencen en el nivel de octavo grado (≈ 13 años ±) en los Estados Unidos. Sin embargo, en algunas escuelas de EE. UU., el álgebra se inicia en el noveno grado.

Álgebra abstracta

El álgebra abstracta extiende los conceptos familiares que se encuentran en el álgebra elemental y la aritmética de números a conceptos más generales. Aquí están los conceptos fundamentales enumerados en álgebra abstracta.

Conjuntos: en lugar de solo considerar los diferentes tipos de números, el álgebra abstracta se ocupa del concepto más general de conjuntos: colecciones de objetos llamados elementos. Todas las colecciones de los tipos familiares de números son conjuntos. Otros ejemplos de conjuntos incluyen el conjunto de todas las matrices de dos por dos, el conjunto de todos los polinomios de segundo grado (ax + bx + c), el conjunto de todos los vectores bidimensionales de un plano y los diversos grupos finitos como los grupos cíclicos, que son los grupos de los números enteros módulo n. La teoría de conjuntos es una rama de la lógica y no técnicamente una rama del álgebra.

Operaciones binarias: La noción de suma (+) se generaliza a la noción de operación binaria (indicada aquí por ∗). La noción de operación binaria no tiene sentido sin el conjunto sobre el que se define la operación. Para dos elementos a y b en un conjunto S, a ∗ b es otro elemento en el conjunto; esta condición se llama cierre. La suma (+), la resta (−), la multiplicación (×) y la división (÷) pueden ser operaciones binarias cuando se definen en diferentes conjuntos, al igual que la suma y la multiplicación de matrices, vectores y polinomios.

Elementos de identidad: Los números cero y uno se generalizan para dar la noción de un elemento de identidad para una operación. El cero es el elemento de identidad para la suma y el uno es el elemento de identidad para la multiplicación. Para un operador binario general ∗ el elemento de identidad e debe satisfacer a ∗ e = a y e ∗ a = a, y es necesariamente único, si existe. Esto es válido para la suma como a + 0 = a y 0 + a = a y la multiplicación a × 1 = a y 1 × a = a. No todos los conjuntos y combinaciones de operadores tienen un elemento de identidad; por ejemplo, el conjunto de los números naturales positivos (1, 2, 3,...) no tiene elemento de identidad para la suma.

Elementos inversos: Los números negativos dan lugar al concepto de elementos inversos. Para la suma, el inverso de a se escribe − a, y para la multiplicación el inverso se escribe a. Un elemento inverso general de dos lados a satisface la propiedad de que a ∗ a = e y a ∗ a = e, donde e es el elemento identidad.

Asociatividad: La suma de números enteros tiene una propiedad llamada asociatividad. Es decir, la agrupación de los números a sumar no afecta la suma. Por ejemplo: (2 + 3) + 4 = 2 + (3 + 4). En general, esto se convierte en (a ∗ b) ∗ c = a ∗ (b ∗ c). Esta propiedad es compartida por la mayoría de las operaciones binarias, pero no por la resta, la división o la multiplicación de octoniones.

Conmutatividad: tanto la suma como la multiplicación de números reales son conmutativas. Es decir, el orden de los números no afecta el resultado. Por ejemplo: 2 + 3 = 3 + 2. En general, esto se convierte en a ∗ b = b ∗ a. Esta propiedad no se cumple para todas las operaciones binarias. Por ejemplo, la multiplicación de matrices y la multiplicación de cuaterniones no son conmutativas.

Grupos

La combinación de los conceptos anteriores da una de las estructuras más importantes de las matemáticas: un grupo. Un grupo es una combinación de un conjunto S y una sola operación binaria ∗, definida de cualquier forma que elija, pero con las siguientes propiedades:

Existe un elemento de identidad e, tal que para cada miembro a de S, e ∗ a y a ∗ e son ambos idénticos a a.
Todo elemento tiene una inversa: para cada miembro a de S, existe un miembro a tal que a ∗ a y a ∗ a son ambos idénticos al elemento identidad.
La operación es asociativa: si a, b y c son miembros de S, entonces (a ∗ b) ∗ c es idéntico a a ∗ (b ∗ c).

Si un grupo también es conmutativo, es decir, para dos miembros cualesquiera a y b de S, a ∗ b es idéntico a b ∗ a, entonces se dice que el grupo es abeliano.

Por ejemplo, el conjunto de números enteros bajo la operación de suma es un grupo. En este grupo, el elemento identidad es 0 y el inverso de cualquier elemento a es su negación, − a. Se cumple el requisito de asociatividad, porque para cualquier entero a, b y c, (a + b) + c = a + (b + c)

Los números racionales distintos de cero forman un grupo bajo la multiplicación. Aquí, el elemento de identidad es 1, ya que 1 × a = a × 1 = a para cualquier número racional a. el inverso de a es1/a, ya que un ×1/a= 1.

Los enteros bajo la operación de multiplicación, sin embargo, no forman un grupo. Esto se debe a que, en general, el inverso multiplicativo de un número entero no es un número entero. Por ejemplo, 4 es un número entero, pero su inverso multiplicativo es1/4, que no es un número entero.

La teoría de grupos se estudia en teoría de grupos. Un resultado importante de esta teoría es la clasificación de grupos finitos simples, publicada principalmente entre 1955 y 1983, que separa los grupos finitos simples en aproximadamente 30 tipos básicos.

Los semigrupos, cuasigrupos y monoides son estructuras algebraicas similares a los grupos, pero con menos restricciones en la operación. Comprenden un conjunto y una operación binaria cerrada, pero no necesariamente satisfacen las otras condiciones. Un semigrupo tiene una operación binaria asociativa pero puede no tener un elemento de identidad. Un monoide es un semigrupo que tiene una identidad pero puede no tener un inverso para cada elemento. Un cuasi-grupo satisface el requisito de que cualquier elemento se puede convertir en cualquier otro mediante una única multiplicación por la izquierda o por la derecha; sin embargo, la operación binaria podría no ser asociativa.

Todos los grupos son monoides y todos los monoides son semigrupos.

Colocar	Números naturales N	Enteros Z	Números racionales QNúmeros reales RNúmeros complejos C	Enteros módulo 3Z /3 Z = {0, 1, 2}
Operación	+	×	+	×	+	−	×	÷	+	×
Cerrado	sí	sí	sí	sí	sí	sí	sí	No	sí	sí
Identidad	0	1	0	1	0	N / A	1	N / A	0	1
Inverso	N / A	N / A	− un	N / A	− un	N / A	1/ un(un ≠ 0)	N / A	0, 2, 1, respectivamente	N/A, 1, 2, respectivamente
De asociación	sí	sí	sí	sí	sí	No	sí	No	sí	sí
Conmutativo	sí	sí	sí	sí	sí	No	sí	No	sí	sí
Estructura	monoide	monoide	grupo abeliano	monoide	grupo abeliano	cuasi-grupo	monoide	cuasi-grupo	grupo abeliano	monoide

Anillos y campos

Los grupos solo tienen una operación binaria. Para explicar completamente el comportamiento de los diferentes tipos de números, es necesario estudiar las estructuras con dos operadores. Los más importantes son los anillos y los campos.

Un anillo tiene dos operaciones binarias (+) y (×), con × distributivo sobre +. Bajo el primer operador (+) forma un grupo abeliano. Bajo el segundo operador (×) es asociativo, pero no necesita tener identidad o inversa, por lo que no se requiere división. El elemento de identidad aditivo (+) se escribe como 0 y el inverso aditivo de a se escribe como − a.

La distributividad generaliza la ley distributiva de los números. Para los números enteros (a + b) × c = a × c + b × c y c × (a + b) = c × a + c × b, y se dice que × es distributivo sobre +.

Los enteros son un ejemplo de un anillo. Los números enteros tienen propiedades adicionales que lo convierten en un dominio integral.

Un campo es un anillo con la propiedad adicional de que todos los elementos excepto el 0 forman un grupo abeliano bajo ×. La identidad multiplicativa (×) se escribe como 1 y el inverso multiplicativo de a se escribe como a.

Los números racionales, los números reales y los números complejos son todos ejemplos de campos.

Etapas del álgebra

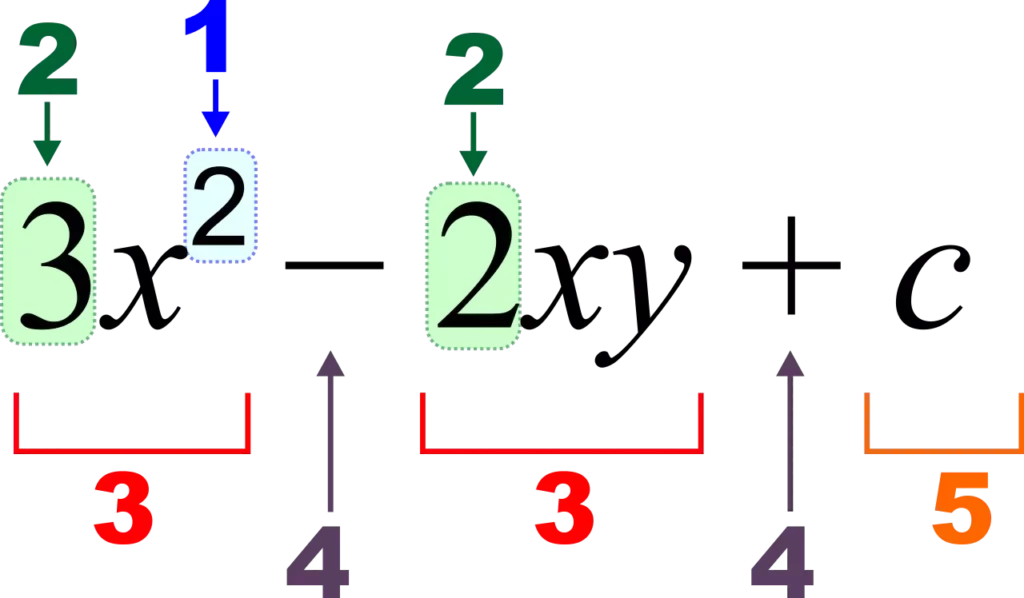
Expresión algebraica

El álgebra no siempre hizo uso del simbolismo que ahora es omnipresente en las matemáticas; en cambio, pasó por tres etapas distintas. Las etapas en el desarrollo del álgebra simbólica son aproximadamente las siguientes:

Álgebra retórica, en la que las ecuaciones se escriben en oraciones completas. Por ejemplo, la forma retórica de ${ estilo de visualización x + 1 = 2}$ es "La cosa más uno es igual a dos" o posiblemente "La cosa más 1 es igual a 2". El álgebra retórica fue desarrollada por primera vez por los antiguos babilonios y siguió siendo dominante hasta el siglo XVI.

Álgebra sincopada, en la que se utiliza algún simbolismo, pero que no contiene todas las características del álgebra simbólica. Por ejemplo, puede haber una restricción de que la resta se puede usar solo una vez dentro de un lado de una ecuación, lo que no es el caso del álgebra simbólica. La expresión algebraica sincopada apareció por primera vez en la Aritmética de Diofanto (siglo III d. C.), seguida por Brahma Sphuta Siddhanta de Brahmagupta (siglo VII).

Álgebra simbólica, en la que se utiliza el simbolismo completo. Los primeros pasos hacia esto se pueden ver en el trabajo de varios matemáticos islámicos como Ibn al-Banna (siglos XIII-XIV) y al-Qalasadi (siglo XV), aunque el álgebra totalmente simbólica fue desarrollada por François Viète (siglo XVI). Más tarde, René Descartes (siglo XVII) introdujo la notación moderna (por ejemplo, el uso de x —ver más abajo) y demostró que los problemas que ocurren en geometría pueden expresarse y resolverse en términos de álgebra (geometría cartesiana).

Tan importante como el uso o la falta de simbolismo en álgebra fue el grado de las ecuaciones que se abordaron. Las ecuaciones cuadráticas jugaron un papel importante en el álgebra temprana; ya lo largo de la mayor parte de la historia, hasta principios del período moderno, todas las ecuaciones cuadráticas se clasificaron como pertenecientes a una de tres categorías.

$x^{2}+px=q$
$x^{2}=px+q$
$x^{2}+q=px$

donde $pag$ y $q$ son positivos. Esta tricotomía se produce porque las ecuaciones cuadráticas de la forma ${ estilo de visualización x^{2}+px+q=0,}$ con $pag$ y $q$ positivo, no tienen raíces positivas.

Entre las etapas retórica y sincopada del álgebra simbólica, los matemáticos clásicos griegos e indios védicos desarrollaron un álgebra constructiva geométrica en la que las ecuaciones algebraicas se resolvían a través de la geometría. Por ejemplo, una ecuación de la forma $x^{2}=A$ se resolvió encontrando el lado de un cuadrado de área $UNA.$

Etapas conceptuales

Además de las tres etapas de expresión de ideas algebraicas, algunos autores reconocieron cuatro etapas conceptuales en el desarrollo del álgebra que ocurrieron junto con los cambios en la expresión. Estas cuatro etapas fueron las siguientes:

Etapa geométrica, donde los conceptos del álgebra son en gran parte geométricos. Esto se remonta a los babilonios y continuó con los griegos, y luego fue revivido por Omar Khayyám.
Etapa de resolución de ecuaciones estáticas, donde el objetivo es encontrar números que satisfagan ciertas relaciones. El alejamiento de la etapa geométrica se remonta a Diofanto y Brahmagupta, pero el álgebra no pasó de manera decisiva a la etapa de resolución de ecuaciones estáticas hasta que Al-Khwarizmi introdujo procesos algorítmicos generalizados para resolver problemas algebraicos.
Etapa de función dinámica, donde el movimiento es una idea subyacente. La idea de una función comenzó a surgir con Sharaf al-Dīn al-Tūsī, pero el álgebra no pasó de manera decisiva a la etapa de función dinámica hasta Gottfried Leibniz.
Etapa abstracta, donde la estructura matemática juega un papel central. El álgebra abstracta es en gran parte un producto de los siglos XIX y XX.

Etimología

La palabra álgebra proviene del árabe: الجبر, romanizado: al-jabr, lit. 'reunión de partes rotas, colocación de huesos' del título del libro de principios del siglo IX Ilm al-jabr wa l-muqābala "La ciencia de restaurar y equilibrar" del matemático y astrónomo persa al-Khwarizmi. En su obra, el término al-jabr se refería a la operación de mover un término de un lado de una ecuación al otro, المقابلة al-muqābala "equilibrar" se refería a sumar términos iguales a ambos lados. Acortado a solo álgeber o álgebraen latín, la palabra finalmente ingresó al idioma inglés durante el siglo XV, ya sea del español, italiano o latín medieval. Originalmente se refería al procedimiento quirúrgico de colocar huesos rotos o dislocados. El significado matemático se registró por primera vez (en inglés) en el siglo XVI.

Diferentes significados de "álgebra"

La palabra "álgebra" tiene varios significados relacionados en matemáticas, como una sola palabra o con calificativos.

Como una sola palabra sin artículo, "álgebra" nombra una amplia parte de las matemáticas.
Como una sola palabra con un artículo o en plural, "un álgebra" o "álgebras" denota una estructura matemática específica, cuya definición precisa depende del contexto. Por lo general, la estructura tiene una suma, una multiplicación y una multiplicación escalar (ver Álgebra sobre un campo). Cuando algunos autores usan el término "álgebra", hacen un subconjunto de las siguientes suposiciones adicionales: asociativa, conmutativa, unitaria y/o de dimensión finita. En álgebra universal, la palabra "álgebra" se refiere a una generalización del concepto anterior, que permite operaciones n-arias.
Con un calificador, existe la misma distinción:
- Sin un artículo, significa una parte de álgebra, como álgebra lineal, álgebra elemental (las reglas de manipulación de símbolos que se enseñan en los cursos elementales de matemáticas como parte de la educación primaria y secundaria) o álgebra abstracta (el estudio de las estructuras algebraicas para ellos mismos).
- Con un artículo, significa una instancia de alguna estructura algebraica, como un álgebra de Lie, un álgebra asociativa o un álgebra de operador de vértice.
- A veces existen ambos significados para el mismo calificador, como en la oración: El álgebra conmutativa es el estudio de los anillos conmutativos, que son álgebras conmutativas sobre los números enteros.

Contenido relacionado

Más resultados...