Adición de Minkowski

En geometría, la suma de Minkowski de dos conjuntos de vectores de posición A y B en el espacio euclidiano se forma sumando cada vector en < i>A a cada vector en B:

${displaystyle A+B={mathbf {a} # Mathbf {b} En A, mathbf {b}$

El Minkowski diferencia (también Sustracción de Minkowski, Minkowski decomposition, o diferencia geométrica) es el inverso correspondiente, donde ${displaystyle (A-B)}$ produce un conjunto que podría resumirse con B para recuperar A. Esto se define como el complemento de la suma de Minkowski del complemento A con el reflejo de B sobre el origen.

${displaystyle -B={mathbf {-b}, 'mathbf {b} in B}$

${displaystyle A-B=left(A^{c}+(-B)right)}$

Esta definición permite una relación simétrica entre la suma y la diferencia de Minkowski. Tenga en cuenta que tomar alternativamente la suma y la diferencia con B no es necesariamente equivalente. La suma puede llenar vacíos que la diferencia tal vez no vuelva a abrir, y la diferencia puede borrar pequeñas islas que la suma no puede recrear de la nada.

${displaystyle (A-B)+Bsubseteq A}$

${displaystyle (A+B)-Bsupseteq A}$

${displaystyle A-B=left(A^{c}+(-B)right)}$

${displaystyle A+B=left(A^{c}-(-B)right)^{c}$

En el procesamiento de imágenes 2D, la suma y diferencia de Minkowski se conocen como dilatación y erosión.

A veces se utiliza una definición alternativa de la diferencia de Minkowski para calcular la intersección de formas convexas. Esto no es equivalente a la definición anterior y no es una operación inversa de la operación de suma. En su lugar, reemplaza la suma vectorial de la suma de Minkowski con una resta vectorial. Si las dos formas convexas se cruzan, el conjunto resultante contendrá el origen.

${displaystyle A-B={mathbf {a} - Mathbf {b} En A, mathbf {b} in B}=A+(-B)}$

El concepto lleva el nombre de Hermann Minkowski.

Ejemplo

Por ejemplo, si tenemos dos sets A y B, cada uno consistente en tres vectores de posición (informalmente, tres puntos), representando los vértices de dos triángulos en ${displaystyle mathbb {R} {2}}$, con coordenadas

${displaystyle A={(1,0),(0,1),(0,-1)}$

y

${displaystyle B={(0,0),(1,1),(1,-1)}$

entonces su suma de Minkowski es

${displaystyle A+B={(1,0),(2,1),(2,-1),(0,1),(1,2),(1,0),(0,-1),(1,0),(1,-2)}}$

que comprende los vértices de un hexágono.

Para Minkowski adición, el cero, ${displaystyle {0},}$ contiene sólo el vector cero, 0, es un elemento de identidad: para cada subconjunto S de un espacio vectorial,

${displaystyle S+{0}=S.}$

El conjunto vacío es importante en la suma de Minkowski, porque el conjunto vacío aniquila todos los demás subconjuntos: para cada subconjunto S de un espacio vectorial, su suma con el conjunto vacío es vacía:

${displaystyle S+emptyset =emptyset.}$

Por otro ejemplo, considere las sumas de Minkowski de bolas abiertas o cerradas en el campo ${displaystyle mathbb {K}$ que es o los números reales ${displaystyle mathbb {R}$ o números complejos ${displaystyle mathbb {C}$ Si ${displaystyle B_{r}:={sin mathbb {K}:$ es la bola cerrada del radio ${displaystyle rin [0,infty]$ centrado en ${displaystyle 0}$ dentro ${displaystyle mathbb {K}$ entonces para cualquier ${displaystyle r,sin [0,infty],}$ ${displaystyle B_{r}+B_{s}=B_{r+s}$ y también ${displaystyle cB_{r}=B_{$ se mantendrá para cualquier escalar ${displaystyle cin mathbb {K}$ tal que el producto ${displaystyle Silencioso$ se define (que sucede cuando ${displaystyle cneq 0}$ o ${displaystyle rneq infty}$). Si ${displaystyle r,s,}$ y ${displaystyle c}$ son todos no cero, entonces las mismas igualdades todavía tendrían ${displaystyle B_{r}$ se define como la bola abierta, en lugar de la bola cerrada, centrada en ${displaystyle 0}$ (la suposición no cero es necesaria porque la bola abierta del radio ${displaystyle 0}$ es el conjunto vacío). La suma de Minkowski de una bola cerrada y una bola abierta es una bola abierta. Más generalmente, la suma de Minkowski de un subconjunto abierto con cualquiera otro set será un subconjunto abierto.

Si ${displaystyle G=left{left(x,1/xright):0neq xin mathbb {R} right}$ es el gráfico de ${displaystyle f(x)={frac {1}{x}}$ y si ${displaystyle Y={0}times mathbb {R}$ es ${displaystyle y}$-eje en ${displaystyle X=Mathbb {R} {2}$ entonces la suma de Minkowski de estos dos subconjuntos cerrados del avión es el conjunto abierto ${displaystyle G+Y={(x,y)in mathbb [R] ^{2}:xneq ♪ ♪♪♪♪Mathbb {R} {2}setminus Sí.$ que consiste en todo lo que no sea el ${displaystyle y}$-Eje. Esto demuestra que la suma de Minkowski de dos sets cerrados no es necesariamente un conjunto cerrado. Sin embargo, la suma de Minkowski de dos subconjuntos cerrados será un subconjunto cerrado si al menos uno de estos conjuntos es también un subconjunto compacto.

Cascos convexos de sumas de Minkowski

La suma de Minkowski se comporta bien con respecto a la operación de tomar cascos convexos, como lo muestra la siguiente proposición:

Para todos los subconjuntos no vacíos ${displaystyle S_{1}$ y ${displaystyle S_{2}$ de un espacio vectorial real, el casco convexo de su suma Minkowski es la suma de Minkowski de sus cascos convexos:

${displaystyle operatorname {Conv} (S_{1}+S_{2})=operatorname {Conv} (S_{1})+operatorname {Conv} (S_{2}). }$

Este resultado es válido de manera más general para cualquier colección finita de conjuntos no vacíos:

${displaystyle operatorname {Conv} left(sum {S_{n}right)=sum operatorname {Conv} (S_{n}). }$

En terminología matemática, las operaciones de suma de Minkowski y de formación de cascos convexos son operaciones de conmutación.

Si ${displaystyle S.$ es un conjunto convexo entonces ${displaystyle mu S+lambda S.$ es también un conjunto convexo; además

${displaystyle mu S+lambda S=(mu +lambda)S}$

para todos ${displaystyle mulambda geq 0}$. Por el contrario, si esta "propiedad distributiva" tiene para todos los números reales no negativos, ${displaystyle mulambda }$, entonces el set es convex.

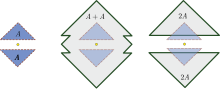
La figura a la derecha muestra un ejemplo de un conjunto no-convexo para el cual ${displaystyle A+Asupsetneq 2A.}$

Un ejemplo en ${displaystyle 1}$ la dimensión es: ${displaystyle B=[1,2]cup [4,5].$ Se puede calcular fácilmente que ${displaystyle 2B=[2,4]cup [8,10]}$ pero ${displaystyle B+B=[2,4]cup [5,7]cup [8,10],}$ de nuevo ${displaystyle B+Bsupsetneq 2B.}$

Minkowski resume actuar linealmente en el perímetro de cuerpos convexos bidimensionales: el perímetro de la suma equivale a la suma de perímetros. Además, si ${displaystyle K}$ es (el interior de) una curva de ancho constante, luego la suma de Minkowski ${displaystyle K}$ y de su ${displaystyle 180^{circ }$ la rotación es un disco. Estos dos hechos se pueden combinar para dar una prueba corta del teorema de Barbier en el perímetro de curvas de ancho constante.

Aplicaciones

La suma de Minkowski juega un papel central en la morfología matemática. Surge en el paradigma de pincelada de los gráficos por computadora 2D (con varios usos, en particular por Donald E. Knuth en Metafont), y como la operación de barrido sólido de los gráficos por computadora 3D. También se ha demostrado que está estrechamente relacionado con la distancia del movimiento de la Tierra y, por extensión, con el transporte óptimo.

Planificación de movimiento

Las sumas de Minkowski se utilizan en la planificación del movimiento de un objeto entre obstáculos. Se utilizan para calcular el espacio de configuración, que es el conjunto de todas las posiciones admisibles del objeto. En el modelo simple de movimiento de traslación de un objeto en el plano, donde la posición de un objeto puede especificarse únicamente por la posición de un punto fijo de este objeto, el espacio de configuración es la suma de Minkowski del conjunto de obstáculos y los obstáculos móviles. Objeto colocado en el origen y girado 180 grados.

Mecanizado con control numérico (NC)

En el mecanizado de control numérico, la programación de la herramienta NC aprovecha el hecho de que la suma de Minkowski de la pieza de corte con su trayectoria da la forma del corte en el material.

Modelado sólido 3D

En OpenSCAD, las sumas de Minkowski se utilizan para delinear una forma con otra forma, creando una combinación de ambas formas.

Teoría de la agregación

Las sumas de Minkowski también se utilizan con frecuencia en la teoría de agregación cuando los objetos individuales que se van a agregar se caracterizan mediante conjuntos.

Detección de colisiones

Las sumas de Minkowski, específicamente las diferencias de Minkowski, se utilizan a menudo junto con los algoritmos GJK para calcular la detección de colisiones para cascos convexos en motores de física.

Algoritmos para calcular sumas de Minkowski

Caso plano

Dos polígonos convexos en el plano

Para dos polígonos convexos P y Q en el plano con m y n vértices, su suma de Minkowski es un polígono convexo con como máximo m + n vértices y se puede calcular en el tiempo O(m + n) mediante un procedimiento muy simple, que puede describirse informalmente de la siguiente manera. Supongamos que se dan los bordes de un polígono y la dirección, digamos, en sentido contrario a las agujas del reloj, a lo largo del límite del polígono. Entonces se ve fácilmente que estas aristas del polígono convexo están ordenadas por ángulo polar. Fusionemos las secuencias ordenadas de los bordes dirigidos de P y Q en un secuencia ordenada única S. Imagine que estos bordes son flechas sólidas que se pueden mover libremente manteniéndolas paralelas a su dirección original. Ensamble estas flechas en el orden de la secuencia S uniendo la cola de la siguiente flecha a la punta de la flecha anterior. Resulta que la cadena poligonal resultante será, de hecho, un polígono convexo que es la suma de Minkowski de P y Q.

Otro

Si un polígono es convexo y otro no, la complejidad de su suma de Minkowski es O(nm). Si ambos son no convexos, su complejidad de suma de Minkowski es O((mn)²).

Suma esencial de Minkowski

También existe una noción de la suma esencial de Minkowski +_e de dos subconjuntos del espacio euclidiano. La suma habitual de Minkowski se puede escribir como

${displaystyle A+B=left{zin mathbb {R} ↑, Acap (z-B)neq emptyset right}$

Así, la suma esencial de Minkowski está definida por

${displaystyle A+_{mathrm {e} }B=left{zin mathbb {R} ^{n}, WordPress,mu left[Acap (z-B)right] Confía0right}$

donde μ denota la medida de Lebesgue n-dimensional. La razón del término "esencial" es la siguiente propiedad de las funciones indicadoras: mientras

${displaystyle 1_{A,+,B}(z)=sup _{x,in ,mathbb [R] ^{n}1_{A}(x)1_{B}(z-x),}$

se puede ver que

${displaystyle 1_{A,+_{mathrm {e},B}(z)=mathop {mathrm {ess,sup} _{x,in ,mathbb [R] ^{n}1_{A}(x)1_{B}(z-x),}$

dónde "ess sup" denota el supremo esencial.

Suma de Lp Minkowski

Para K y L subconjuntos compactos convexo en ${displaystyle mathbb {R} {} {}} {fn}}$, la suma de Minkowski se puede describir por la función de soporte de los conjuntos de convex:

${displaystyle ¿Qué?$

Para p ≥ 1, Firey definió L^p Minkowski sum K +_p L de conjuntos compactos convex K y L dentro ${displaystyle mathbb {R} {} {}} {fn}}$ que contiene el origen

${displaystyle ¿Qué?$

Según la desigualdad de Minkowski, la función h_K+pL es nuevamente homogénea y convexa positiva y, por tanto, la función de soporte de una convexa compacta colocar. Esta definición es fundamental en la teoría L^p de Brunn-Minkowski.