Acoplamiento mecánico

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Un enlace mecánico o acoplamiento mecánico es un conjunto de sistemas conectados para gestionar las fuerzas y el movimiento. El movimiento de un cuerpo, o enlace, se estudia mediante geometría, por lo que el enlace se considera rígido. Las conexiones entre enlaces se modelan proporcionando un movimiento ideal, rotación pura o deslizamiento, por ejemplo, y se denominan articulaciones. Un eslabón modelado como una red de eslabones rígidos y uniones ideales se llama cadena cinemática.

Los enlaces pueden construirse a partir de cadenas abiertas, cadenas cerradas o una combinación de cadenas abiertas y cerradas. Cada eslabón de una cadena está conectado por una articulación a uno o más eslabones. Por lo tanto, una cadena cinemática se puede modelar como un gráfico en el que los enlaces son caminos y las articulaciones son vértices, lo que se denomina gráfico de enlace.

El movimiento de una articulación ideal generalmente se asocia con un subgrupo del grupo de desplazamientos euclidianos. El número de parámetros en el subgrupo se denomina grados de libertad (DOF) de la articulación. Los enlaces mecánicos generalmente están diseñados para transformar una fuerza de entrada y un movimiento dados en una fuerza y un movimiento de salida deseados. La relación entre la fuerza de salida y la fuerza de entrada se conoce como la ventaja mecánica del varillaje, mientras que la relación entre la velocidad de entrada y la velocidad de salida se conoce como relación de velocidad. La relación de velocidad y la ventaja mecánica se definen de modo que produzcan el mismo número en un enlace ideal.

Una cadena cinemática, en la que un eslabón está fijo o estacionario, se llama mecanismo, y un eslabón diseñado para ser estacionario se llama estructura.

Historia

Arquímedes aplicó la geometría al estudio de la palanca. En la década de 1500, el trabajo de Arquímedes y Héroe de Alejandría fueron las fuentes principales de la teoría de máquinas. Fue Leonardo da Vinci quien aportó una energía inventiva a las máquinas y al mecanismo.

A mediados de la década de 1700, la máquina de vapor era cada vez más importante y James Watt se dio cuenta de que se podía aumentar la eficiencia mediante el uso de diferentes cilindros para la expansión y condensación del vapor. Esto impulsó su búsqueda de un enlace que pudiera transformar la rotación de una manivela en un deslizamiento lineal y resultó en su descubrimiento de lo que se llama el enlace de Watt. Esto condujo al estudio de encadenamientos que pudieran generar líneas rectas, aunque sea de forma aproximada; e inspiró al matemático JJ Sylvester, quien dio una conferencia sobre el enlace de Peaucellier, que genera una línea recta exacta a partir de una manivela giratoria.

El trabajo de Sylvester inspiró a AB Kempe, quien demostró que los vínculos para la suma y la multiplicación podían ensamblarse en un sistema que trazaba una curva algebraica dada. El procedimiento de diseño de Kempe ha inspirado la investigación en la intersección de la geometría y la informática.

A finales de 1800, F. Reuleaux, ABW Kennedy y L. Burmester formalizaron el análisis y la síntesis de sistemas de vínculos mediante geometría descriptiva, y PL Chebyshev introdujo técnicas analíticas para el estudio y la invención de vínculos.

A mediados de la década de 1900, F. Freudenstein y GN Sandor utilizaron la computadora digital recientemente desarrollada para resolver las ecuaciones de bucle de un enlace y determinar sus dimensiones para una función deseada, iniciando el diseño de enlaces asistido por computadora. En dos décadas, estas técnicas informáticas eran parte integral del análisis de sistemas de máquinas complejas y el control de manipuladores de robots.

RE Kaufman combinó la capacidad de la computadora para calcular rápidamente las raíces de las ecuaciones polinómicas con una interfaz gráfica de usuario para unir las técnicas de Freudenstein con los métodos geométricos de Reuleaux y Burmester y formar KINSYN, un sistema interactivo de gráficos por computadora para el diseño de vínculos.

El estudio moderno de enlaces incluye el análisis y diseño de sistemas articulados que aparecen en robots, máquinas herramienta y sistemas de tensegridad y accionados por cable. Estas técnicas también se están aplicando a sistemas biológicos e incluso al estudio de proteínas.

Movilidad

La configuración de un sistema de enlaces rígidos conectados por nudos ideales se define por un conjunto de parámetros de configuración, como los ángulos alrededor de un nudo giratorio y los deslizamientos a lo largo de nudos prismáticos medidos entre enlaces adyacentes. Las restricciones geométricas del enlace permiten el cálculo de todos los parámetros de configuración en términos de un conjunto mínimo, que son los parámetros de entrada. El número de parámetros de entrada se denomina movilidad, o grado de libertad, del sistema de enlace.

Un sistema de n cuerpos rígidos que se mueven en el espacio tiene 6 n grados de libertad medidos con respecto a un marco fijo. Incluye este marco en el conteo de cuerpos, para que la movilidad sea independiente de la elección del marco fijo, entonces tenemos M = 6(N − 1), donde N = n + 1 es el número de cuerpos en movimiento más el cuerpo fijo.

Las articulaciones que conectan cuerpos en este sistema eliminan grados de libertad y reducen la movilidad. Específicamente, las bisagras y los deslizadores imponen cada uno cinco restricciones y, por lo tanto, eliminan cinco grados de libertad. Es conveniente definir el número de restricciones c que impone un nudo en términos de la libertad f del nudo, donde c = 6 − f. En el caso de una bisagra o corredera, que son uniones de un grado de libertad, tenemos f = 1 y por lo tanto c = 6 − 1 = 5.

Por lo tanto, la movilidad de un sistema de eslabonamiento formado por n eslabones móviles y j nudos, cada uno con fi, _i = 1,..., j , grados de libertad se puede calcular como, $M=6n-sum_{{i=1}}^{j}(6-f_{i})=6(N-1-j)+sum_{{i=1}}^{j} f_{i},$

donde N incluye el enlace fijo. Esto se conoce como la ecuación de Kutzbach-Grübler

Hay dos casos especiales importantes: (i) una cadena abierta simple y (ii) una cadena cerrada simple. Una cadena abierta simple consta de n eslabones móviles conectados de extremo a extremo por j uniones, con un extremo conectado a un eslabón de tierra. Así, en este caso N = j + 1 y la movilidad de la cadena es $M=sum_{{i=1}}^{j} f_{i}.$

Para una cadena cerrada simple, n eslabones móviles están conectados de extremo a extremo por n +1 uniones, de modo que los dos extremos están conectados al eslabón de tierra formando un bucle. En este caso, tenemos N = j y la movilidad de la cadena es $M=sum_{{i=1}}^{j} f_{i}-6.$

Un ejemplo de una cadena abierta simple es un manipulador de robot en serie. Estos sistemas robóticos se construyen a partir de una serie de enlaces conectados por seis articulaciones prismáticas o giratorias de un grado de libertad, por lo que el sistema tiene seis grados de libertad.

Un ejemplo de una cadena cerrada simple es el enlace espacial de cuatro barras RSSR (revoluto-esférico-esférico-revoluto). La suma de las libertades de estos nudos es ocho, por lo que la movilidad del varillaje es dos, donde uno de los grados de libertad es el giro del acoplador alrededor de la línea que une los dos nudos en S.

Movimiento plano y esférico.

Es una práctica común diseñar el sistema de articulación de modo que el movimiento de todos los cuerpos esté restringido a descansar en planos paralelos, para formar lo que se conoce como articulación plana. También es posible construir el sistema de enlace para que todos los cuerpos se muevan sobre esferas concéntricas, formando un enlace esférico. En ambos casos, los grados de libertad del vínculo ahora son tres en lugar de seis, y las restricciones impuestas por los nudos ahora son c = 3 − f.

En este caso, la fórmula de movilidad viene dada por $M = 3(N- 1 - j)+ sum_{i=1}^j f_i,$

y tenemos los casos especiales,

cadena abierta simple plana o esférica,

$M = sum_{i=1}^j f_i,$

cadena cerrada simple plana o esférica,

$M = sum_{i=1}^j f_i - 3.$

Un ejemplo de una cadena plana simple cerrada es el eslabón plano de cuatro barras, que es un bucle de cuatro barras con cuatro uniones de un grado de libertad y, por lo tanto, tiene una movilidad M = 1.

Articulaciones

Las articulaciones más familiares para los sistemas de articulación son la articulación giratoria, o articulada, denotada por una R, y la articulación prismática o deslizante, denotada por una P. La mayoría de las demás articulaciones utilizadas para los vínculos espaciales se modelan como combinaciones de articulaciones giratorias y prismáticas. Por ejemplo,

la junta cilíndrica consiste en una cadena en serie RP o PR construida de modo que los ejes de las articulaciones angulares y prismáticas sean paralelos,
la junta universal consta de una cadena en serie RR construida de manera que los ejes de las juntas giratorias se cruzan en un ángulo de 90°;
la junta esférica consiste en una cadena en serie RRR para la cual cada uno de los ejes de la junta articulada se cortan en un mismo punto;
la unión plana se puede construir como una cadena en serie plana RRR, RPR y PPR que tiene tres grados de libertad.

Análisis y síntesis de vínculos

La principal herramienta matemática para el análisis de un vínculo se conoce como las ecuaciones cinemáticas del sistema. Esta es una secuencia de transformación de cuerpo rígido a lo largo de una cadena en serie dentro del enlace que ubica un enlace flotante en relación con el marco de tierra. Cada cadena en serie dentro del enlace que conecta este enlace flotante a tierra proporciona un conjunto de ecuaciones que deben ser satisfechas por los parámetros de configuración del sistema. El resultado es un conjunto de ecuaciones no lineales que definen los parámetros de configuración del sistema para un conjunto de valores de los parámetros de entrada.

Freudenstein introdujo un método para usar estas ecuaciones para el diseño de un enlace plano de cuatro barras para lograr una relación específica entre los parámetros de entrada y la configuración del enlace. L. Burmester introdujo otro enfoque para el diseño de eslabonamiento plano de cuatro barras y se llama teoría de Burmester.

Vínculos planos de un grado de libertad

La fórmula de movilidad proporciona una forma de determinar el número de enlaces y juntas en un enlace plano que produce un enlace de un grado de libertad. Si requerimos que la movilidad de un enlace plano sea M = 1 y f _i = 1, el resultado es ${ estilo de visualización M = 3 (N-1-j) + j = 1, !}$

o ${displaystyle j={frac {3}{2}}N-2.!}$

Esta fórmula muestra que el enlace debe tener un número par de enlaces, por lo que tenemos

N = 2, j = 1: este es un enlace de dos barras conocido como palanca;
N = 4, j = 4: este es el enlace de cuatro barras;
N = 6, j = 7: este es un enlace de seis barras [tiene dos enlaces que tienen tres uniones, llamados enlaces ternarios, y hay dos topologías de este enlace dependiendo de cómo se conecten estos enlaces. En la topología de Watt, los dos enlaces ternarios están conectados por una junta. En la topología de Stephenson, los dos enlaces ternarios están conectados por enlaces binarios;
N = 8, j = 10: el enlace de ocho barras tiene 16 topologías diferentes;
N = 10, j = 13: el enlace de 10 barras tiene 230 topologías diferentes,
N = 12, j = 16: la barra de 12 tiene 6856 topologías.

Consulte Sunkari y Schmidt para conocer la cantidad de topologías de 14 y 16 barras, así como la cantidad de enlaces que tienen dos, tres y cuatro grados de libertad.

El eslabonamiento plano de cuatro barras es probablemente el eslabonamiento más simple y común. Es un sistema de un grado de libertad que transforma una rotación de manivela de entrada o un desplazamiento del deslizador en una rotación o deslizamiento de salida.

Ejemplos de vínculos de cuatro barras son:

el balancín de manivela, en el que la manivela de entrada gira completamente y el enlace de salida se balancea hacia adelante y hacia atrás;
la manivela deslizante, en la que la manivela de entrada gira y la corredera de salida se mueve hacia adelante y hacia atrás;
mecanismos de enlace de arrastre, en los que la manivela de entrada gira completamente y arrastra la manivela de salida en un movimiento de rotación total.

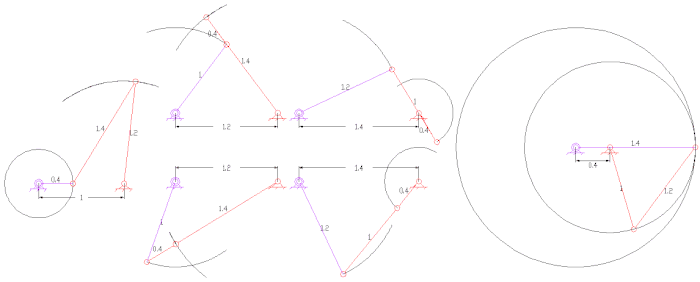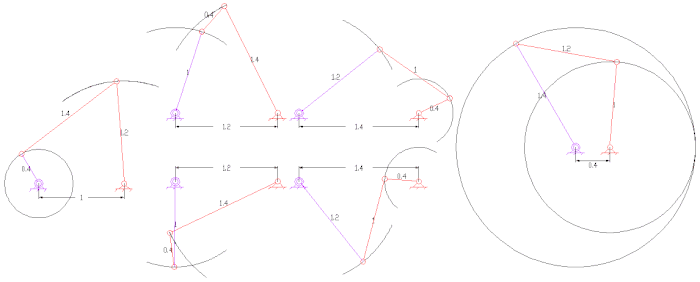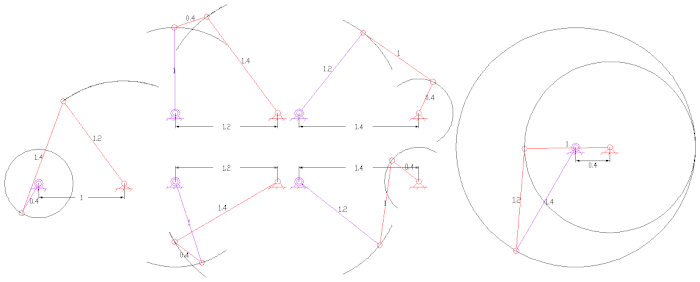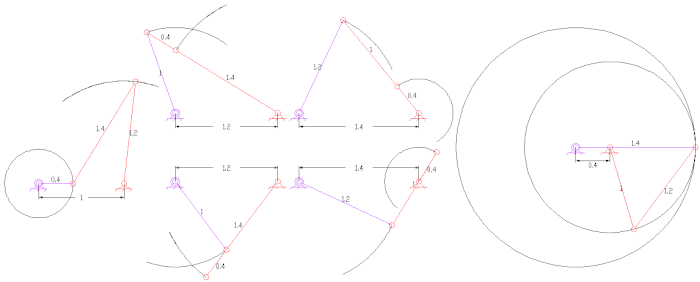Tipos de enlaces de cuatro barras con longitudes de enlace asignadas a cada enlace: observe el enlace más corto

S y el enlace más largo

L de cada uno de estos mecanismos.

Otros vínculos interesantes

Pantógrafo (cuatro barras, dos DOF)
Los vínculos de cinco barras a menudo tienen engranajes engranados para dos de los vínculos, lo que crea un vínculo de un DOF. Pueden proporcionar una mayor transmisión de potencia con más flexibilidad de diseño que los enlaces de cuatro barras.
El enlace de Jansen es un mecanismo de patas de ocho barras que fue inventado por el escultor cinético Theo Jansen.
El enlace Klann es un enlace de seis barras que forma un mecanismo de patas;
Los mecanismos de palanca son enlaces de cuatro barras que están dimensionados para que puedan plegarse y bloquearse. Las posiciones de conmutación están determinadas por la colinealidad de dos de los enlaces móviles. El varillaje está dimensionado para que alcance una posición de palanca justo antes de plegarse. La gran ventaja mecánica permite que la manivela de entrada deforme el varillaje lo suficiente como para empujarlo más allá de la posición de palanca. Esto bloquea la entrada en su lugar. Los mecanismos de palanca se utilizan como abrazaderas.

Mecanismos de línea recta

Movimiento paralelo de James Watt y enlace de Watt
Varillaje Peaucellier-Lipkin, el primer varillaje plano que crea una salida perfecta en línea recta a partir de una entrada rotatoria; ocho barras, un DOF.
Un enlace de Scott Russell, que convierte el movimiento lineal en (casi) movimiento lineal en una línea perpendicular a la entrada.
Enlace de Chebyshev, que proporciona un movimiento casi recto de un punto con un enlace de cuatro barras.
Enlace de Hoekens, que proporciona un movimiento casi recto de un punto con un enlace de cuatro barras.
Enlace de Sarrus, que proporciona el movimiento de una superficie en una dirección normal a otra.
Inversor de Hart, que proporciona un movimiento rectilíneo perfecto sin guías deslizantes.

Vínculos biológicos

Los sistemas de ligamiento están ampliamente distribuidos en los animales. Mees Muller, quien también diseñó un nuevo sistema de clasificación que es especialmente adecuado para los sistemas biológicos, proporcionó la descripción general más completa de los diferentes tipos de enlaces en animales. Un ejemplo bien conocido son los ligamentos cruzados de la rodilla.

Una diferencia importante entre los vínculos biológicos y de ingeniería es que las barras giratorias son raras en biología y que, por lo general, solo es posible una pequeña gama de lo teóricamente posible debido a restricciones mecánicas adicionales (especialmente la necesidad de administrar sangre). Los vínculos biológicos con frecuencia cumplen. A menudo, una o más barras están formadas por ligamentos y, a menudo, los enlaces son tridimensionales. Se conocen sistemas de eslabones acoplados, así como eslabonamientos de cinco, seis e incluso siete barras. Sin embargo, los enlaces de cuatro barras son, con mucho, los más comunes.

Los enlaces se pueden encontrar en las articulaciones, como la rodilla de los tetrápodos, el corvejón de las ovejas y el mecanismo craneal de las aves y los reptiles. Este último es responsable del movimiento ascendente del pico superior en muchas aves.

Los mecanismos de enlace son especialmente frecuentes y múltiples en la cabeza de los peces óseos, como los lábridos, que han desarrollado muchos mecanismos de alimentación especializados. Especialmente avanzados son los mecanismos de vinculación de la protrusión mandibular. Para la alimentación por succión, un sistema de conexiones de cuatro barras es responsable de la apertura coordinada de la boca y la expansión tridimensional de la cavidad bucal. Otros enlaces son responsables de la protrusión del premaxilar.

Los enlaces también están presentes como mecanismos de bloqueo, como en la rodilla del caballo, lo que permite que el animal duerma de pie, sin una contracción muscular activa. En la alimentación de pivote, utilizada por ciertos peces óseos, un enlace de cuatro barras al principio bloquea la cabeza en una posición doblada ventralmente mediante la alineación de dos barras. La liberación del mecanismo de bloqueo lanza la cabeza hacia arriba y mueve la boca hacia la presa en 5 a 10 ms.

Galería de imágenes

Generador de funciones basculante-deslizador que aproxima la función Log(u) para 1 < u < 10.
Generador de funciones de control deslizante que aproxima la función Tan(u) para 0 < u < 45°.
Centrodes fijos y móviles de un eslabonamiento de cuatro barras
Varillaje de cuatro barras de piñón y cremallera
mecanismo RTRTR
mecanismo RTRTR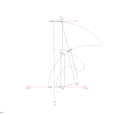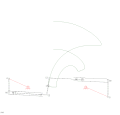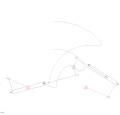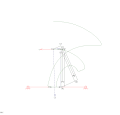
Mecanismos de engranajes de cinco barras.
Mecanismo de manivela deslizante 3D
Personaje animado de Pinocho
Conicógrafo de Crawford
Mecanismo desplegable plegable hacia afuera
Mecanismo desplegable plegable hacia adentro

Contenido relacionado

Más resultados...