Aclaramiento (farmacología)

En farmacología, autorización ()Cltot{displaystyle Cl_{tot}) es un parámetro farmacocinético que representa la eficiencia de la eliminación de drogas. Esta es la tasa de eliminación de una sustancia dividida por su concentración. El parámetro también indica el volumen teórico del plasma del cual una sustancia sería completamente eliminada por unidad de tiempo. Por lo general, la limpieza se mide en L/h o mL/min. La cantidad refleja la tasa de eliminación de drogas dividida por concentración de plasma. La extracción, por otro lado, es una medición de la cantidad de una sustancia eliminada del cuerpo por unidad tiempo (por ejemplo, mg/min, μg/min, etc.). Mientras que la limpieza y la excreción de una sustancia están relacionadas, no son lo mismo. El concepto de autorización fue descrito por Thomas Addis, graduado de la Escuela Médica de la Universidad de Edimburgo.

Las sustancias del cuerpo pueden eliminarse mediante varios órganos, incluidos los riñones, el hígado, los pulmones, etc. Por lo tanto, el aclaramiento corporal total es igual a la suma del aclaramiento de la sustancia por cada órgano (p. ej., aclaramiento renal + aclaramiento hepático + aclaramiento pulmonar = aclaramiento corporal total). Sin embargo, para muchos fármacos el aclaramiento es únicamente una función de la excreción renal. En estos casos, el aclaramiento es casi sinónimo de aclaramiento renal o aclaramiento plasmático renal. Cada sustancia tiene un aclaramiento específico que depende de cómo la nefrona maneja la sustancia. El aclaramiento es función de 1) filtración glomerular, 2) secreción de los capilares peritubulares a la nefrona y 3) reabsorción de la nefrona a los capilares peritubulares. El aclaramiento es variable en la cinética de orden cero porque se elimina una cantidad constante del fármaco por unidad de tiempo, pero es constante en la cinética de primer orden, porque la cantidad de fármaco eliminada por unidad de tiempo cambia con la concentración del fármaco en la sangre.

El aclaramiento puede referirse al volumen de plasma del cual se elimina la sustancia (es decir, se aclara) por unidad de tiempo o, en algunos casos, se pueden discutir los aclaramientos intercompartimentales cuando se hace referencia a la redistribución entre Compartimentos corporales como plasma, músculo y grasa.

Definición

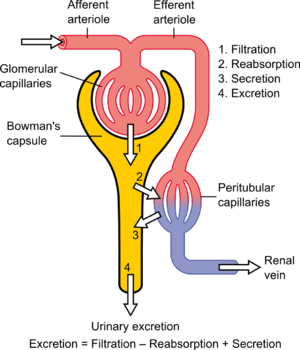
El aclaramiento de una sustancia es el volumen de plasma que contiene la misma cantidad de sustancia que se ha eliminado del plasma por unidad de tiempo.

Cuando nos referimos a la función del riñón, se considera que el aclaramiento es la cantidad de líquido filtrado de la sangre que es procesada por los riñones o la cantidad de sangre limpiada cada vez. porque tiene las unidades de caudal volumétrico [ volumen por unidad de tiempo ]. Sin embargo, no se refiere a un valor real; "el riñón no elimina completamente una sustancia del flujo plasmático renal total." Desde una perspectiva de transferencia de masa y fisiológicamente, el flujo sanguíneo volumétrico (hacia la máquina de diálisis y/o el riñón) es sólo uno de varios factores que determinan la concentración sanguínea y la eliminación de una sustancia del cuerpo. Otros factores incluyen el coeficiente de transferencia de masa, el flujo de dializado y el flujo de recirculación de dializado para hemodiálisis, y la tasa de filtración glomerular y la tasa de reabsorción tubular, para el riñón. Una interpretación fisiológica del aclaramiento (en estado estacionario) es que el aclaramiento es una relación entre la generación de masa y la concentración en sangre (o plasma).

Su definición se deriva de la ecuación diferencial que describe la caída exponencial y se utiliza para modelar la función renal y la función de la máquina de hemodiálisis:

VdCdt=− − K⋅ ⋅ C+mÍ Í {displaystyle V{frac {dC} {dt}=-Kcdot C+{dot {m}}

()1)

Donde:

• mÍ Í {displaystyle { dot {}}} es la tasa de generación masiva de la sustancia - se supone que es una constante, es decir, no una función del tiempo (igual a cero para sustancias/drogas extranjeras) [mmol/min] o [mol/s]
• t es tiempo o tiempo de diálisis desde la inyección de la sustancia/drogas [min] o [s]
• V es el volumen de distribución o agua total del cuerpo [L] o [m]³]
• K es la autorización [mL/min] o [m³/s]
• C es la concentración [mmol/L] o [mol/m³] (en los Estados Unidos a menudo [mg/mL]

De las definiciones anteriores se desprende que dCdt{displaystyle {frac {dc} {dt}} es el primer derivado de la concentración con respecto al tiempo, es decir, el cambio de concentración con el tiempo.

Se deriva de un equilibrio de masas.

La limpieza de una sustancia se expresa a veces como el inverso de la constante del tiempo que describe su tasa de eliminación del cuerpo dividido por su volumen de distribución (o agua total del cuerpo).

En estado estable, se define como la tasa de generación masiva de una sustancia (que equivale a la tasa de extracción de masa) dividida por su concentración en la sangre.

Aclaramiento, vida media y volumen de distribución

Existe una relación importante entre la limpieza, la eliminación de la vida media y el volumen de distribución. La tasa de eliminación constante de un fármaco Kel{displaystyle K_{el} es equivalente a la liquidación total dividida por el volumen de distribución

Kel=CltotVd{displaystyle K_{el}={dfrac {Cl_{tot} {V_{d}}}

(nota el uso de Cl y no K, para no confundir con Kel{displaystyle K_{el}). Pero... Kel{displaystyle K_{el} es también equivalente a In⁡ ⁡ 2{displaystyle ln 2} dividida por la tasa de eliminación de la mitad de vida t1/2{displaystyle T_{1/2}, Kel=In⁡ ⁡ 2t1/2{displaystyle K_{el}={dfrac {ln} 2}{t_{1/2}}}. Así, Cltot=In⁡ ⁡ 2⋅ ⋅ Vdt1/2{displaystyle Cl_{tot}={dfrac {ln 2cdot ¿Qué?. Esto significa, por ejemplo, que un aumento de la limpieza total da lugar a una disminución de la tasa de eliminación media vida, siempre que el volumen de distribución sea constante. Derivación de estas ecuaciones se puede encontrar en, por ejemplo. Farmacología de Rang y Dale

Efecto de la proteína plasmática

Para sustancias que exhiben una unión sustancial a proteínas plasmáticas, el aclaramiento generalmente depende de la concentración total (libre + unida a proteínas) y no de la concentración libre.

La mayoría de las sustancias plasmáticas tienen reguladas principalmente sus concentraciones libres, que por lo tanto permanecen iguales, por lo que la unión extensa a proteínas aumenta la concentración plasmática total (libre + unida a proteínas). Esto disminuye el aclaramiento en comparación con lo que habría ocurrido si la sustancia no se uniera a las proteínas. Sin embargo, la tasa de eliminación de masa es la misma, porque depende sólo de la concentración de sustancia libre y es independiente de la unión a las proteínas plasmáticas, incluso con el hecho de que las proteínas plasmáticas aumentan su concentración en el glomérulo renal distal a medida que el plasma se filtra en Bowman. 39;s, porque los aumentos relativos en las concentraciones de sustancia-proteína y proteína no ocupada son iguales y, por lo tanto, no producen unión ni disociación neta de sustancias de las proteínas plasmáticas, lo que da una concentración plasmática constante de sustancia libre en todo el glomérulo, que también habría sido el caso sin ninguna unión a proteínas plasmáticas.

Sin embargo, en otros sitios además de los riñones, donde el aclaramiento se realiza mediante proteínas de transporte de membrana en lugar de filtración, la unión extensa a las proteínas plasmáticas puede aumentar el aclaramiento al mantener la concentración de sustancia libre bastante constante en todo el lecho capilar, inhibiendo una disminución en el aclaramiento causada por disminución de la concentración de sustancia libre a través del capilar.

Derivación de la ecuación

Ecuación 1 se deriva de un equilibrio de masa:

Δ Δ mcuerpo=()− − mÍ Í Fuera.+mÍ Í dentro+mÍ Í Gen.)Δ Δ t{displaystyle Delta m_{text{body}=(-{dot {m} {fn} {fnh} {fnh}} {fnh} {fnh}} {fn}}}} {fn}} {fnh}}}}} {fnh}}}}} {\fnh}f}}}\fnhfnh}}} {\f}}}}}}}}}}\\\\\\fn}}}}}}}}}}}}}}\\\\\f}}}}}}}}}}}\\\\\\\f}}}}}}}}}}}}}}}}}}}}}}}}}\\\\\\f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {m} {fn} {fnh}} {fnh} {fnh}} {fnh}}}} {fn}} {fn}}}} {fnh}}}}} {\fn}}}}}}}} {fn}}}}}}}} {f}}}}}}}} { {m}_{text{gen}}) Delta t}

()2)

Donde:

• Δ Δ t{displaystyle Delta t} es un período de tiempo
• Δ Δ mcuerpo{displaystyle Delta m_{text{body}} el cambio en la masa de la toxina en el cuerpo durante Δ Δ t{displaystyle Delta t}
• mÍ Í dentro{displaystyle {dot {fn}} {fn}} {fn}}} {fn}} {fn}} {fnfn}}}}} {fn}}}}}} {fnK}}}}}}} {fn}}}}}}}}}}}}}}}}}} es la tasa de ingesta de toxina
• mÍ Í Fuera.{displaystyle { dot {}_{text{out}} es la tasa de eliminación de toxina
• mÍ Í Gen.{fnMicrosoft Sans Serif}}} es la tasa de generación de toxina

En palabras, la ecuación anterior establece:

El cambio en la masa de una toxina dentro del cuerpo (Δ Δ m{displaystyle Delta m}) durante algún tiempo Δ Δ t{displaystyle Delta t} es igual a la ingesta de toxina más la generación de toxina menos la eliminación de toxina.

Desde

mcuerpo=C⋅ ⋅ V{displaystyle ### {text{body}=Ccdot V.

()3)

y

mÍ Í Fuera.=K⋅ ⋅ C{displaystyle { dot {fnh}}=Kcdot C}

()4)

La ecuación A1 se puede reescribir como:

Δ Δ ()C⋅ ⋅ V)=()− − K⋅ ⋅ C+mÍ Í dentro+mÍ Í Gen.)Δ Δ t{displaystyle Delta (Ccdot V)=left(-Kcdot C+{dot {m} {fn} {fnh} {fnh} {fnh}} {fnh}}} {fn}}}}} {fn} Bueno... Delta t}

()5)

Si uno golpea el dentro y Gen. términos juntos, es decir. mÍ Í =mÍ Í dentro+mÍ Í Gen.{displaystyle { dot}={dot {m} {fn} {fnh}} {fnh} {fnh}} {fnh}}}} {fn}} {fn}}}} {fnh}}}}} {\fn}}}}}}}} {fn}}}}}}}} {f}}}}}}}} { {m}_{text{gen}} y divisiones por Δ Δ t{displaystyle Delta t} el resultado es una ecuación de diferencia:

Δ Δ ()C⋅ ⋅ V)Δ Δ t=− − K⋅ ⋅ C+mÍ Í {displaystyle {frac {Delta (Ccdot V)}{ Delta .

()6)

Si uno aplica el límite Δ Δ t→ → 0{displaystyle Delta tto 0} uno obtiene una ecuación diferencial:

d()C⋅ ⋅ V)dt=− − K⋅ ⋅ C+mÍ Í {displaystyle {frac {d(Ccdot V)}{dt}=-Kcdot C+{dot {m}}

()7)

Utilizando la regla del producto esto puede ser reescrito como:

CdVdt+VdCdt=− − K⋅ ⋅ C+mÍ Í {displaystyle C{frac ¿Qué? {dC} {dt}=-Kcdot C+{dot {m}}

()8)

Si uno asume que el cambio de volumen no es significativo, es decir. CdVdt=0{displaystyle C{frac {dt}=0}, el resultado es la Ecuación 1:

Solución a la ecuación diferencial

La solución general de la ecuación diferencial anterior (1) es:

C=mÍ Í K+()Co− − mÍ Í K)e− − K⋅ ⋅ tV{displaystyle C={frac { dot {m} {K}+left(C_{o}-{frac} {fnMicrosoft Sans Serif} {fnMicroc {Kcdot} .

()9)

Dónde:

• C_o es la concentración al comienzo de la diálisis o la concentración inicial de la sustancia/drogas (después de haber distribuido) [mmol/L] o [mol/m³]
• e es la base del logaritmo natural

Solución de estado de vapor

La solución de la ecuación diferencial anterior (9) en el tiempo infinito (estado estacionario) es:

CJUEGO JUEGO =mÍ Í K{displaystyle C_{infty}={frac {dot {} {}} {}}}

()10a)

La ecuación anterior ( 10a ) puede reescribirse como:

K=mÍ Í CJUEGO JUEGO {displaystyle K={frac} {m} {C_{infty}}} {}} {c}} {c}} {c}} {c}}}}} {c}}}}}} {c}}}} {cH}}}} {c}}}} {c}}}} {c}}}}}}} {c}}}}}}}}}}}}}}}}}}}}}}} {c}}}}}}}}}}}}}}} {c}}}}}}} {c}}}}}}}}}}}}}}}}}}}}}}}} {c}}}}}}}}}}}}}} {c}}}}}}}}}}}}}}} {c}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

()10b)

La ecuación anterior (10b) deja clara la relación entre la eliminación de masa y la limpieza. Se afirma que (con una generación de masa constante) la concentración y el aclaramiento varían inversamente entre sí. Si se aplica a la creatinina (es decir, el aclaramiento de creatinina), se deduce de la ecuación que si la creatinina sérica duplica el aclaramiento se reduce a la mitad y si la creatinina sérica se cuadriplica, el aclaramiento se cuadriplica.

Medición del aclaramiento renal

El aclaramiento renal se puede medir con una recolección cronometrada de orina y un análisis de su composición con la ayuda de la siguiente ecuación (que se deriva directamente de la derivación de (10b)):

K=CU⋅ ⋅ QCB{displaystyle K={frac {C_{U}cdot ¿Qué?

()11)

Dónde:

• K es la autorización [mL/min]
• C_U es la concentración de orina [mmol/L] (en los EE.UU. a menudo [mg/mL])
• Q es el flujo de orina (volumen/tiempo) [mL/min] (a menudo [mL/24 h])
• C_B es la concentración de plasma [mmol/L] (en los EE.UU. a menudo [mg/mL])

Cuando la sustancia "C" es la creatinina, una sustancia química endógena que se excreta sólo por filtración; el aclaramiento es una aproximación de la tasa de filtración glomerular. La depuración de inulina se utiliza con menos frecuencia para determinar con precisión la tasa de filtración glomerular.

Nota: la ecuación anterior (11) es válida sólo para la condición de estado estable. Si la sustancia que se está eliminando no está en una concentración plasmática constante (es decir, no está en estado estacionario), se debe obtener K del (completo) solución de la ecuación diferencial (9).