Aceleración gravitacional
En física, la aceleración gravitacional es la aceleración de un objeto en caída libre dentro del vacío (y por lo tanto sin experimentar resistencia). Esta es la ganancia constante de velocidad causada exclusivamente por la atracción gravitacional. Todos los cuerpos aceleran en el vacío a la misma velocidad, independientemente de las masas o composiciones de los cuerpos; la medición y análisis de estas tasas se conoce como gravimetría.
En un punto fijo de la superficie, la magnitud de la gravedad de la Tierra resulta del efecto combinado de la gravitación y la fuerza centrífuga de la rotación de la Tierra. En diferentes puntos de la superficie de la Tierra, la aceleración de caída libre oscila entre 9,764 y 9,834 m/s2 (32,03 a 32,26 pies/s2), dependiendo de altitud, latitud y longitud. Un valor estándar convencional se define exactamente como 9,80665 m/s² (aproximadamente 32,1740 pies/s²). Las ubicaciones con variaciones significativas de este valor se conocen como anomalías de gravedad. Esto no tiene en cuenta otros efectos, como la flotabilidad o la resistencia al arrastre.
Relación con la Ley Universal
La ley de gravitación universal de Newton establece que existe una fuerza gravitacional entre dos masas cualesquiera que es igual en magnitud para cada masa y está alineada para atraer las dos masas entre sí. La fórmula es:
Donde y son dos masas, es la constante gravitacional, y es la distancia entre las dos masas de punto.

Utilizando la forma integral de la Ley de Gauss, esta fórmula se puede extender a cualquier par de objetos de los cuales uno sea mucho más masivo que el otro, como un planeta en relación con cualquier artefacto a escala humana. Las distancias entre los planetas y entre los planetas y el Sol son (en muchos órdenes de magnitud) mayores que los tamaños del Sol y los planetas. En consecuencia, tanto el Sol como los planetas pueden considerarse masas puntuales y aplicarse la misma fórmula a los movimientos planetarios. (Como los planetas y los satélites naturales forman pares de masa comparable, la distancia 'r' se mide desde los centros de masa comunes de cada par en lugar de la distancia total directa entre los centros de los planetas).
Si una masa es mucho mayor que la otra, es conveniente tomarla como referencia observacional y definirla como fuente de un campo gravitacional de magnitud y orientación dada por:
Donde es la masa de la fuente de campo (más grande), y es un vector de unidad dirigido desde la fuente de campo a la masa de muestra (smaller). El signo negativo indica que la fuerza es atractiva (puntos hacia atrás, hacia la fuente).
Entonces la fuerza de atracción vector en una masa de muestra puede expresarse como:
Aquí. es la aceleración sin fricción y caída libre sostenida por la masa de muestreo bajo la atracción de la fuente gravitacional. Es un vector orientado hacia la fuente de campo, de magnitud medida en unidades de aceleración. El vector de aceleración gravitacional depende sólo sobre cuán masiva es la fuente de campo es y en la distancia 'r' a la masa de la muestra . No depende de la magnitud de la masa de muestra pequeña.
Este modelo representa el "campo lejano" Aceleración gravitacional asociada a un cuerpo masivo. Cuando las dimensiones de un cuerpo no son triviales en comparación con las distancias de interés, se puede utilizar el principio de superposición para masas diferenciales para una distribución de densidad supuesta en todo el cuerpo con el fin de obtener un modelo más detallado del cuerpo. campo" aceleración gravitacional. Para los satélites en órbita, el modelo de campo lejano es suficiente para realizar cálculos aproximados de altitud versus período, pero no para una estimación precisa de la ubicación futura después de múltiples órbitas.
Los modelos más detallados incluyen (entre otras cosas) el abultamiento en el Ecuador para la Tierra, y las concentraciones irregulares de masa (debido a los impactos meteorológicos) para la Luna. La misión Gravity Recovery and Climate Experiment (GRACE) lanzada en 2002 consiste en dos sondas, apodadas "Tom" y "Jerry", en órbita polar alrededor de la Tierra midiendo diferencias en la distancia entre las dos sondas para determinar más precisamente el campo gravitatorio alrededor de la Tierra, y para rastrear los cambios que ocurren con el tiempo. Del mismo modo, la misión de recuperación de gravedad y laboratorios de interior entre 2011 y 2012 consistió en dos sondas ("Ebb" y "Flow") en órbita polar alrededor de la Luna para determinar más precisamente el campo gravitacional para futuros propósitos de navegación, e inferir información sobre el maquillaje físico de la Luna.
Gravedades comparativas de la Tierra, el Sol, la Luna y los planetas
La tabla siguiente muestra aceleraciónes gravitacionales comparativos en la superficie del Sol, la luna de la Tierra, cada uno de los planetas en el Sistema Solar y sus lunas principales, Ceres, Plutón y Eris. Para cuerpos gaseosos, la "superficie" se toma para significar superficie visible: las nubes de los gigantes del gas (Júpiter, Saturno, Urano y Neptuno), y la fotosfera del Sol. Los valores de la tabla no han sido descalificados para el efecto de fuerza centrífuga de la rotación del planeta (y las velocidades del viento en la nube para los gigantes del gas) y por lo tanto, generalmente hablando, son similares a la gravedad real que se experimentaría cerca de los polos. Para referencia el tiempo que tomaría un objeto caer 100 metros, la altura de un rascacielos, se muestra, junto con la velocidad máxima alcanzada. La resistencia al aire es descuidada.
| Cuerpo | Múltiplo de Gravedad de la Tierra | m/s2 | ft/s2 | Notas | Hora de caer 100 m y velocidad máxima alcanzada | |
|---|---|---|---|---|---|---|
| Sol | 27.90 | 274.1 | 899 | 0,85 s | 843 km/h (524 mph) | |
| Mercurio | 0,3770 | 3.703 | 12.15 | 7.4 s | 98 km/h (61 mph) | |
| Venus | 0.9032 | 8.872 | 29.11 | 4.8 s | 152 km/h (94 mph) | |
| Tierra | 1 | 9.8067 | 32.174 | 4.5 s | 159 km/h (99 mph) | |
| Luna | 0.1655 | 1.625 | 5.33 | 11.1 s | 65 km/h (40 mph) | |
| Marte | 0,3895 | 3.728 | 12.23 | 7.3 s | 98 km/h (61 mph) | |
| Ceres | 0,029 | 0,28 | 0.92 | 26.7 s | 27 km/h (17 mph) | |
| Júpiter | 2.640 | 25.93 | 85.1 | 2.8 s | 259 km/h (161 mph) | |
| Io | 0.182 | 1.789 | 5.87 | 10.6 s | 68 km/h (42 mph) | |
| Europa | 0.134 | 1.314 | 4.31 | 12.3 s | 58 km/h (36 mph) | |
| Ganymede | 0.145 | 1.426 | 4.68 | 11.8 s | 61 km/h (38 mph) | |
| Callisto | 0.126 | 1.24 | 4.1 | 12,7 s | 57 km/h (35 mph) | |
| Saturno | 1.139 | 11.19 | 36,7 | 4.2 s | 170 km/h (110 mph) | |
| Titan | 0.138 | 1.3455 | 4.414 | 12.2 s | 59 km/h (37 mph) | |
| Urano | 0.917 | 9.01 | 29.6 | 4,7 s | 153 km/h (95 mph) | |
| Titania | 0,039 | 0,379 | 1.24 | 23.0 s | 31 km/h (19 mph) | |
| Oberon | 0,035 | 0,347 | 1.14 | 24.0 s | 30 km/h (19 mph) | |
| Neptuno | 1.148 | 11.28 | 37.0 | 4.2 s | 171 km/h (106 mph) | |
| Triton | 0,079 | 0,79 | 2.56 | 16.0 s | 45 km/h (28 mph) | |
| Plutón | 0,0621 | 0.610 | 2.00 | 18.1 s | 40 km/h (25 mph) | |
| Eris | 0,0814 | 0,8 | 2.6 | (aprox.) | 15.8 s | 46 km/h (29 mph) |
Relatividad general
En la teoría de la relatividad general de Einstein, la gravitación es un atributo del espacio-tiempo curvo en lugar de deberse a una fuerza propagada entre cuerpos. En la teoría de Einstein, las masas distorsionan el espacio-tiempo en sus proximidades y otras partículas se mueven en trayectorias determinadas por la geometría del espacio-tiempo. La fuerza gravitacional es una fuerza ficticia. No existe aceleración gravitacional, ya que la aceleración propia y, por tanto, las cuatro aceleraciones de los objetos en caída libre son cero. En lugar de sufrir una aceleración, los objetos en caída libre viajan a lo largo de líneas rectas (geodésicas) en el espacio-tiempo curvo.
Campo gravitacional
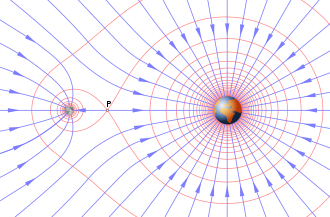
En física, un campo gravitacional o campo de aceleración gravitacional es un campo vectorial utilizado para explicar las influencias que un cuerpo se extiende al espacio alrededor de sí mismo. Un campo gravitacional se utiliza para explicar fenómenos gravitacionales, como el campo de fuerza gravitacional ejercido en otro cuerpo masivo. Tiene dimensión de aceleración (L/T)2) y se mide en unidades de newtons por kilogramo (N/kg) o, equivalentemente, en metros por segundo cuadrado (m/s2).
En su concepto original, la gravedad era una fuerza entre las masas de puntos. Después de Isaac Newton, Pierre-Simon Laplace intentó modelar la gravedad como algún tipo de campo de radiación o fluido, y desde el siglo XIX, las explicaciones de la gravedad en la mecánica clásica se han enseñado generalmente en términos de un modelo de campo, en lugar de un punto de atracción. Resulta del gradiente espacial del campo potencial gravitacional.
En la relatividad general, en lugar de dos partículas que se atraen, las partículas distorsionan el tiempo espacial a través de su masa, y esta distorsión es lo que se percibe y mide como una "fuerza". En tal modelo uno declara que la materia se mueve de ciertas maneras en respuesta a la curvatura del tiempo espacial, y que hay o no fuerza gravitatoria, o esa gravedad es una fuerza ficticia.
La gravedad se distingue de otras fuerzas por su obediencia al principio de equivalencia.










