5 cubos

5-cube penteract (pent)
Tipo	uniforme 5-polytope
Símbolo Schläfli	{4,3,3,3}
Coxeter diagrama
4 caras	10	tesseracts
Celdas	40	cubos
Caras	80	cuadrados
Edges	80
Vertices	32
Vertex figure	5 celdas
Coxeter group	B5, [4,3]3Orden 3840
Doble	5-orthoplex
Punto de base	(1,1,1,1,1,1)
Circumradius	sqrt(5)/2 = 1.118034
Propiedades	convex, isogonal regular, Hanner politope

En geometría de cinco dimensiones, un cubo de cinco dimensiones es el nombre que se le da a un hipercubo de cinco dimensiones con 32 vértices, 80 aristas, 80 caras cuadradas, 40 celdas cúbicas y 10 teseractos de cuatro caras.

Se representa mediante el símbolo de Schläfli {4,3,3,3} o {4,3³}, construido como 3 teseractos, {4,3,3}, alrededor de cada cresta cúbica.

Es parte de una familia de hipercubos infinitos. El dual de un 5-cubo es el 5-ortoplex, de la familia infinita de ortoplexes.

Al aplicar una operación de alternancia, eliminando los vértices alternos del 5-cubo, se crea otro 5-politopo uniforme, llamado 5-demicubeo, que también forma parte de una familia infinita llamada semihipercubos.

El cubo de 5 puede verse como un panal teseractico de orden 3 sobre una esfera de 4. Está relacionado con el panal teseractico euclidiano de 4 espacios (orden 4) y con el panal teseractico hiperbólico paracompacto de orden 5.

Esta matriz de configuración representa el cubo de 5 elementos. Las filas y columnas corresponden a vértices, aristas, caras, celdas y 4 caras. Los números diagonales indican cuántos elementos de cada elemento hay en el cubo de 5 elementos. Los números no diagonales indican cuántos elementos de la columna hay en el elemento de la fila o en él.

${\displaystyle {\begin{bmatrix}{\begin{matrix}32 tendría5 igual10 tendría5\2 rest80 tendría4\4\4 limit4\4 implica4 tendría3\8 implica3\8 implica12 implica6 limitada2\16 simultáneamente2\16 consecutivo32 queda24 queda8 queda10\end{matrix}}}\end{bmatrix}}}}}}}}}}}}}}} {\$

Las coordenadas cartesianas de los vértices de un cubo de 5 ejes centrado en el origen y con una longitud de arista de 2 son

(±1,±1,±1,±1,±1),

mientras que el interior de este cubo de 5 está formado por todos los puntos (x₀, x₁, x₂, x₃, x₄) con -1 < x_i < 1 para todo i.

Las proyecciones del plano de Coxeter de n-cubos en los grupos de Coxeter B_k se proyectan en grafos de k-cubos, con potencias de dos vértices superpuestos en los grafos proyectivos.

Proyecciones ortoográficas

Coxeter avión	B5	B4 D5	B3 D4 / A2
Gráfico
Simetría Dihedral	[10]	[8]	[6]
Coxeter avión	Otros	B2	A3
Gráfico
Simetría Dihedral	[2]	[4]	[4]

Más proyecciones ortográficos

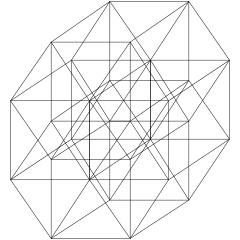Wireframe skew direction

B5 Coxeter avión

Gráfico

Gráfico de linaje.

Proyecciones de perspectiva

Una proyección de perspectiva 3D a 2D de proyección estereográfica 4D a 3D del diagrama Schlegel 5D a 4D.

Net

4D net of the 5-cube, perspective projected into 3D.

El 5-cubo se puede proyectar hacia abajo a 3 dimensiones con un sobre icosahedron rhombic. Hay 22 vértices exteriores, y 10 vértices interiores. Los 10 vértices interiores tienen el casco convexo de un antiprismo pentagonal. El proyecto 80 bordes en 40 bordes externos y 40 internos. El proyecto de 40 cubos en rhombohedra dorada que se puede utilizar para diseccionar el icosahedro rhombic. Los vectores de proyección son u = {1, φ, 0, -1, φ}, v = {φ, 0, 1, φ, 0}, w = {0, 1, φ, 0, -1}, donde φ es la relación de oro, ${\fnMicroc} {1+{\sqrt {}} {2}}}} {}}} {}}}}}} {}}} {}}}}} {}} {}}}} {}}}} {}}}}}}} {}}}} {}}}}}} {}}}}} {}}}}}}} {}}}}}} {}}}}}} {}}}}}}}}}}} {}}}}}}}}} {}}}}}}}}}}}}} {}}}}}}}}}}}}}} {}}}}}} {}}}}}} {}}}}}}}}}}}}} {}}}}}}}}}}} {}}}}} {}}}}}}}}}}}}} {}}}}}}}}}}}} {}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}$.

rhombic icosahedron		5-cube
Perspectiva	ortogonal

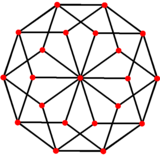También es posible proyectar penteractos en un espacio tridimensional, de forma similar a como se proyecta un cubo en un espacio bidimensional.

Una proyección de perspectiva 3D de un penteract bajo una rotación simple sobre el plano ortogonal W1-W2

Una proyección de perspectiva 3D de un penteracto que sufre una doble rotación sobre los planos X-W1 y Z-W2 ortogonal

El 5-cube la simetría del grupo Coxeter B₅, estructura abstracta ${\displaystyle C_{2}\wr S_{5}$, orden 3840, que contiene 25 hiperplanos de reflexión. El símbolo Schläfli para el 5-cubo, {4,3,3}, coincide con la simetría de la notación de Coxeter [4,3,3].

Todos los hipercubos tienen formas de simetría inferior construidas como prismas. El 5-cubo tiene 7 formas prismáticas a partir del 5-ortótopo inferior, { }⁵, y hacia arriba, ya que las aristas ortogonales están restringidas a tener la misma longitud. Los vértices de un prisma son iguales al producto de los vértices de los elementos. Las aristas de un prisma se pueden dividir en la cantidad de aristas de un elemento multiplicada por la cantidad de vértices de todos los demás elementos.

Descripción	Símbolo Schläfli	Coxeter-Dynkin diagrama	Vertices	Edges	Coxeter notation Simmetría	Orden
5-cube	{4,3,3,3}		32	80	[4,3,3]	3840
teseractic prism	{4,3,3}×{}		16×2 = 32	64 + 16 = 80	[4,3,2]	768
cube-square duoprism	{4,3}×{4}		8×4 = 32	48 + 32 = 80	[4,3,2,4]	384
cube-rectangle duoprism	{4,3}×{ }2		8×22 = 32	48 + 2×16 = 80	[4,3,2,2]	192
prisma del duoprismo cuadrado	{4}2#		42× 2 = 32	2×32 + 16 = 80	[4,2,4,2]	128
duoprismo cuadrado-rectangular paralelizado	{4}×{}3		4×23 = 32	32 + 3×16 = 80	[4,2,2,2]	64
5 orthotope	{}5		25 = 32	5×16 = 80	[2,2,2,2,2]	32

El 5-cubo es el quinto de una serie de hipercubos:

Proyecciones ortográficas de polígono Petrie

Serie de línea	Plaza	Cube	4-cube	5-cube	6-cube	7-cube	8-cube	9-cube	10-cube

El poliedro oblicuo regular {4,5| 4} se puede realizar dentro del cubo de 5, con sus 32 vértices, 80 aristas y 40 caras cuadradas, y las otras 40 caras cuadradas del cubo de 5 se convierten en agujeros cuadrados.

Este politopo es uno de los 31 politopos 5 uniformes generados a partir del cubo 5 o el ortoplex 5 regular.

Pólvora B5
β5	t1β5	t2γ5	t1γ5	γ5	t0,1β5	t0,2β5	t1,2β5
t0,3β5	t1,3γ5	t1,2γ5	t0,4γ5	t0,3γ5	t0,2γ5	t0,1γ5	t0,1,2β5
t0,1,3β5	t0,2,3β5	t1,2,3γ5	t0,1,4β5	t0,2,4γ5	t0,2,3γ5	t0,1,4γ5	t0,1,3γ5
t0,1,2γ5	t0,1,2,3β5	t0,1,2,4β5	t0,1,3,4γ5	t0,1,2,4γ5	t0,1,2,3γ5	t0,1,2,3,4γ5

• H.S.M. Coxeter:
  • Coxeter, Polytopes regulares, (3a edición, 1973), Dover Edition, ISBN 0-486-61480-8, p. 296, Tabla I (iii): Polytopes regulares, three regular polytopes in n-dimensions (n≥5)
  • Kaleidoscopios: Escrituras seleccionadas de H.S.M. Coxeter, editado por F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
    • H.S.M. Coxeter, Polytops regulares y semi regulares I[Mat. Zeit. 46 (1940) 380-407, MR 2,10]
    • H.S.M. Coxeter, Polytopes regulares y semi-regulares II[Math. Zeit. 188 (1985) 559-591]
    • H.S.M. Coxeter, Polytopes regulares y semi-regulares III[Mat. Zeit. 200 (1988) 3-45]
• Norman Johnson Uniform Polytopes, Manuscrito (1991)
  • N.W. Johnson: The The The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
• Klitzing, Richard. "5D uniforme politopes (polytera) o3o3o4x - pent".

• Weisstein, Eric W. "Hypercube". MathWorld.
• Olshevsky, George. "Measure polytope". Glosario para Hyperspace. Archivado desde el original el 4 de febrero de 2007.
• Multidimensional Glosario: hipercubo Garrett Jones
• Maltsev, Nick E. https://www.asymptotos.com/wp-content/uploads/2023/07/Cube_5.html