Velocidade da luz
A velocidade da luz no vácuo, comumente denotada como c, é uma constante física universal que é exatamente igual a 299.792.458 metros por segundo (aproximadamente 300.000 quilômetros por segundo; 186.000 milhas por segundo; 671 milhões de milhas por hora). De acordo com a teoria da relatividade especial, c é o limite superior para a velocidade com que a matéria ou energia convencional (e, portanto, qualquer sinal transportando informações) podem viajar pelo espaço.
Todas as formas de radiação eletromagnética, incluindo a luz visível, viajam à velocidade da luz. Para muitos efeitos práticos, a luz e outras ondas eletromagnéticas parecerão propagar-se instantaneamente, mas para longas distâncias e medições muito sensíveis, a sua velocidade finita tem efeitos perceptíveis. Qualquer luz estelar vista na Terra vem de um passado distante, permitindo aos humanos estudar a história do universo visualizando objetos distantes. Ao se comunicar com sondas espaciais distantes, pode levar de minutos a horas para que os sinais viajem. Na computação, a velocidade da luz fixa o atraso mínimo de comunicação. A velocidade da luz pode ser usada em medições de tempo de vôo para medir grandes distâncias com precisão extremamente alta.
Ole Rømer demonstrou pela primeira vez em 1676 que a luz não viaja instantaneamente, estudando o movimento aparente da lua de Júpiter, Io. Medições progressivamente mais precisas de sua velocidade surgiram ao longo dos séculos seguintes. Num artigo publicado em 1865, James Clerk Maxwell propôs que a luz era uma onda eletromagnética e, portanto, viajava à velocidade c. Em 1905, Albert Einstein postulou que a velocidade da luz c em relação a qualquer referencial inercial é uma constante e é independente de o movimento da fonte de luz. Ele explorou as consequências desse postulado derivando a teoria da relatividade e, ao fazê-lo, mostrou que o parâmetro c tinha relevância fora do contexto da luz e do eletromagnetismo.
Partículas sem massa e perturbações de campo, como ondas gravitacionais, também viajam à velocidade c no vácuo. Tais partículas e ondas viajam a c independentemente do movimento da fonte ou do referencial inercial do observador. Partículas com massa de repouso diferente de zero podem ser aceleradas para se aproximar de c mas nunca podem alcançá-lo, independentemente do referencial em que sua velocidade é medido. Nas teorias especial e geral da relatividade, c inter-relaciona espaço e tempo e também aparece na famosa equação de equivalência massa-energia, E = mc2.
Em alguns casos, os objetos ou ondas podem parecer viajar mais rápido que a luz (por exemplo, velocidades de fase das ondas, aparecimento de certos objetos astronômicos de alta velocidade e efeitos quânticos específicos). Entende-se que a expansão do universo excede a velocidade da luz além de um certo limite.
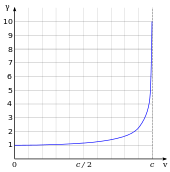
A velocidade com que a luz se propaga através de materiais transparentes, como vidro ou ar, é menor que c; da mesma forma, a velocidade das ondas eletromagnéticas em cabos de aço é mais lenta que c. A proporção entre c e a velocidade v no qual a luz viaja em um material é chamado de índice de refração n do material (n = < span class="texhtml mvar" style="font-style:italic;">c/ v). Por exemplo, para a luz visível, o índice de refração do vidro é normalmente em torno de 1,5, o que significa que a luz no vidro viaja a c/1,5 ≈ 200000 km/s (124000 mi/s); o índice de refração do ar para a luz visível é de cerca de 1,0003, então a velocidade da luz no ar é cerca de 90 km/s (56 mi/s) mais lenta que c.
Valor numérico, notação e unidades
A velocidade da luz no vácuo é geralmente indicada por c minúsculo, para "constante" ou o latim celeritas (que significa 'rapidez, celeridade'). Em 1856, Wilhelm Eduard Weber e Rudolf Kohlrausch usaram c para uma constante diferente que mais tarde foi mostrada como sendo igual a √ 2 vezes a velocidade da luz no vácuo. Historicamente, o símbolo V foi usado como um símbolo alternativo para a velocidade da luz, introduzido por James Clerk Maxwell em 1865. Em 1894, Paul Drude redefiniu c com seu significado moderno. Einstein usou V em seus artigos originais em alemão sobre a relatividade especial em 1905, mas em 1907 ele mudou para c, que até então se tornou o símbolo padrão para a velocidade da luz.
Às vezes, c é usado para a velocidade das ondas em qualquer meio material, e c0 para a velocidade da luz no vácuo. Esta notação subscrita, que é endossada na literatura oficial do SI, tem a mesma forma que as constantes eletromagnéticas relacionadas: a saber, μ0 para a permeabilidade ao vácuo ou constante magnética, ε0 para a permissividade do vácuo ou constante elétrica, e Z0 para a impedância do espaço livre. Este artigo usa c exclusivamente para a velocidade da luz no vácuo.
Uso em sistemas de unidades
Desde 1983, a constante c foi definida no Sistema Internacional de Unidades (SI) como exatamente < span class="nowrap">299792458 m/s; esta relação é usada para definir o metro como exatamente a distância que a luz viaja no vácuo em 1⁄299792458 de segundo. Usando o valor de c, bem como uma medição precisa do segundo, pode-se assim estabelecer um padrão para o metro. Como uma constante física dimensional, o valor numérico de c é diferente para diferentes sistemas de unidades. Por exemplo, em unidades imperiais, a velocidade da luz é aproximadamente 186282 milhas por segundo, ou aproximadamente 30 centímetros por nanossegundo.
Em ramos da física em que c aparece com frequência, como na relatividade, é comum usar sistemas de unidades naturais de medida ou o sistema de unidades geometrizado onde c = 1. Usando essas unidades, c não aparece explicitamente porque a multiplicação ou divisão por 1 não afeta o resultado. Sua unidade de segundo-luz por segundo ainda é relevante, mesmo que omitida.
Papel fundamental na física
A velocidade com que as ondas de luz se propagam no vácuo é independente tanto do movimento da fonte da onda quanto do referencial inercial do observador. Essa invariância da velocidade da luz foi postulada por Einstein em 1905, após ser motivado pela teoria do eletromagnetismo de Maxwell e pela falta de evidências de movimento contra o éter luminífero. Desde então, foi consistentemente confirmado por muitos experimentos. Só é possível verificar experimentalmente que a velocidade bidirecional da luz (por exemplo, de uma fonte para um espelho e vice-versa) é independente do quadro, porque é impossível medir a velocidade unidirecional da luz (por exemplo, de uma fonte a um detector distante) sem alguma convenção sobre como os relógios na fonte e no detector devem ser sincronizados.
Ao adotar a sincronização de Einstein para os relógios, a velocidade unidirecional da luz torna-se igual à velocidade bidirecional da luz, por definição. A teoria da relatividade especial explora as consequências desta invariância de c com a suposição de que as leis da física são as mesmas em todos os referenciais inerciais. Uma consequência é que c é a velocidade com que todas as partículas e ondas sem massa, incluindo a luz, devem viajar no vácuo.
A relatividade especial tem muitas implicações contra-intuitivas e verificadas experimentalmente. Isso inclui a equivalência de massa e energia (E = mc2), contração do comprimento (objetos em movimento encurtam) e dilatação do tempo (relógios em movimento funcionam mais lentamente). O fator γ pelo qual os comprimentos se contraem e os tempos se dilatam é conhecido como fator de Lorentz e é dado por γ = (1 − v2/c2)−1/2, onde v é a velocidade do objeto. A diferença entre γ e 1 é insignificante para velocidades muito mais lentas que c, como a maioria das velocidades diárias. Nesse caso, a relatividade especial é muito aproximada da relatividade galileana - mas aumenta em velocidades relativísticas e diverge para o infinito à medida que v se aproxima de c. Por exemplo, um fator de dilatação do tempo de γ = 2 ocorre a uma velocidade relativa de 86,6% da velocidade da luz (v = 0,866 c). Da mesma forma, um fator de dilatação de tempo de γ = 10 ocorre a 99,5% da velocidade da luz (v = 0,995 c).
Os resultados da relatividade especial podem ser resumidos tratando o espaço e o tempo como uma estrutura unificada conhecida como espaço-tempo (com c relacionando as unidades de espaço e tempo) e exigindo que as teorias físicas satisfaçam uma condição especial. simetria chamada invariância de Lorentz, cuja formulação matemática contém o parâmetro c. A invariância de Lorentz é uma suposição quase universal para teorias físicas modernas, como a eletrodinâmica quântica, a cromodinâmica quântica, o Modelo Padrão da física de partículas e a relatividade geral. Como tal, o parâmetro c é onipresente na física moderna, aparecendo em muitos contextos não relacionados à luz. Por exemplo, a relatividade geral prevê que c é também a velocidade da gravidade e das ondas gravitacionais, e as observações das ondas gravitacionais têm sido consistentes com esta previsão. Em referenciais não inerciais (espaço-tempo gravitacionalmente curvo ou referenciais acelerados), a velocidade local da luz é constante e igual a c, mas a velocidade da luz pode diferir de c quando medido a partir de um quadro de referência remoto, dependendo de como as medições são extrapoladas para a região.
Geralmente presume-se que constantes fundamentais como c têm o mesmo valor em todo o espaço-tempo, o que significa que não dependem da localização e não variam com o tempo. No entanto, foi sugerido em várias teorias que a velocidade da luz pode ter mudado ao longo do tempo. Nenhuma evidência conclusiva para tais mudanças foi encontrada, mas elas continuam sendo objeto de pesquisas em andamento.
É geralmente assumido que a velocidade da luz é isotrópica, o que significa que tem o mesmo valor independentemente da direção em que é medida. As observações das emissões dos níveis de energia nuclear em função da orientação dos núcleos emissores em um campo magnético (ver experimento Hughes-Drever) e de ressonadores ópticos rotativos (ver experimentos Resonator) colocaram limites rigorosos nas possíveis duas vias. anisotropia.
Limite máximo de velocidade
De acordo com a relatividade especial, a energia de um objeto com massa de repouso m e velocidade v é dada por γmc2, onde γ é o fator de Lorentz definido acima. Quando v é zero, γ é igual a um, dando origem ao famoso E = mc2 fórmula para equivalência massa-energia. O fator γ se aproxima do infinito à medida que v se aproxima de c, e seria necessária uma quantidade infinita de energia para acelerar um objeto com massa até a velocidade de luz. A velocidade da luz é o limite superior para as velocidades de objetos com massa de repouso positiva, e os fótons individuais não podem viajar mais rápido que a velocidade da luz. Isto é estabelecido experimentalmente em muitos testes de energia e momento relativísticos.

De modo mais geral, é impossível que sinais ou energia viajem mais rápido que c. Um argumento para isso decorre da implicação contra-intuitiva da relatividade especial conhecida como relatividade da simultaneidade. Se a distância espacial entre dois eventos A e B for maior que o intervalo de tempo entre eles multiplicado por c, então há referenciais nos quais A precede B, outros em que B precede A e outros em que são simultâneos. Como resultado, se algo viajasse mais rápido que c em relação a um referencial inercial, estaria viajando para trás no tempo em relação a outro referencial, e a causalidade seria violada. Nesse quadro de referência, um "efeito" poderia ser observado antes de sua 'causa'. Tal violação da causalidade nunca foi registrada e levaria a paradoxos como o antitelefone taquiônico.
Observações e experimentos mais rápidos que a luz
Há situações em que pode parecer que matéria, energia ou sinais que transportam informações viajam a velocidades superiores a c, mas isso não acontece. Por exemplo, como é discutido na propagação da luz em uma seção média abaixo, muitas velocidades de onda podem exceder c. A velocidade de fase dos raios X através da maioria dos vidros pode exceder rotineiramente c, mas a velocidade de fase não determina a velocidade com que as ondas transmitem informações.
Se um feixe de laser passar rapidamente por um objeto distante, o ponto de luz pode se mover mais rápido que c, embora o movimento inicial do ponto seja atrasado devido ao tempo que a luz leva para chegar para o objeto distante na velocidade c. No entanto, as únicas entidades físicas que se movem são o laser e a luz emitida, que viaja à velocidade c do laser até as diversas posições do ponto. Da mesma forma, uma sombra projetada em um objeto distante pode se mover mais rápido que c, após um atraso no tempo. Em nenhum dos casos qualquer matéria, energia ou informação viaja mais rápido que a luz.
A taxa de variação na distância entre dois objetos em um referencial em relação ao qual ambos estão se movendo (sua velocidade de fechamento) pode ter um valor superior a c. No entanto, isso não representa a velocidade de qualquer objeto medido em um único referencial inercial.
Certos efeitos quânticos parecem ser transmitidos instantaneamente e, portanto, mais rápido que c, como no paradoxo EPR. Um exemplo envolve os estados quânticos de duas partículas que podem ser emaranhadas. Até que qualquer uma das partículas seja observada, elas existem numa superposição de dois estados quânticos. Se as partículas forem separadas e o estado quântico de uma partícula for observado, o estado quântico da outra partícula será determinado instantaneamente. No entanto, é impossível controlar qual o estado quântico que a primeira partícula assumirá quando for observada, pelo que a informação não pode ser transmitida desta forma.
Outro efeito quântico que prevê a ocorrência de velocidades mais rápidas que a luz é chamado de efeito Hartman: sob certas condições, o tempo necessário para uma partícula virtual atravessar uma barreira é constante, independentemente da espessura da barreira. Isso poderia resultar em uma partícula virtual cruzando uma grande lacuna mais rápido que a luz. No entanto, nenhuma informação pode ser enviada usando este efeito.
O chamado movimento superluminal é visto em certos objetos astronômicos, como os jatos relativísticos de rádio-galáxias e quasares. No entanto, estes jactos não se movem a velocidades superiores à velocidade da luz: o movimento superluminal aparente é um efeito de projecção causado por objectos que se movem perto da velocidade da luz e se aproximam da Terra num pequeno ângulo em relação à linha de visão: uma vez que a luz que foi emitido quando o jato estava mais distante demorou mais para chegar à Terra, o tempo entre duas observações sucessivas corresponde a um tempo maior entre os instantes em que os raios de luz foram emitidos.
Uma experiência de 2011, onde se observou que neutrinos viajavam mais rápido que a luz, revelou-se devido a um erro experimental.
Em modelos do Universo em expansão, quanto mais distantes as galáxias estão umas das outras, mais rapidamente se separam. Por exemplo, infere-se que galáxias distantes da Terra estão se afastando da Terra com velocidades proporcionais às suas distâncias. Além de uma fronteira chamada esfera de Hubble, a taxa com que a distância da Terra aumenta torna-se maior do que a velocidade da luz. Estas taxas de recessão, definidas como o aumento da distância adequada por tempo cosmológico, não são velocidades no sentido relativístico. Velocidades de recessão cosmológica mais rápidas que a luz são apenas um artefato coordenado.
Propagação da luz
Na física clássica, a luz é descrita como um tipo de onda eletromagnética. O comportamento clássico do campo eletromagnético é descrito pelas equações de Maxwell, que prevêem que a velocidade c com a qual as ondas eletromagnéticas (como a luz) se propagam no vácuo está relacionada à capacitância e indutância distribuídas. do vácuo, também conhecida respectivamente como constante elétrica ε0 e constante magnética μ0, pela equação
Na física quântica moderna, o campo eletromagnético é descrito pela teoria da eletrodinâmica quântica (QED). Nesta teoria, a luz é descrita pelas excitações fundamentais (ou quanta) do campo eletromagnético, chamadas fótons. No QED, os fótons são partículas sem massa e, portanto, de acordo com a relatividade especial, viajam à velocidade da luz no vácuo.
Extensões de QED nas quais o fóton tem massa foram consideradas. Em tal teoria, sua velocidade dependeria de sua frequência, e a velocidade invariante c da relatividade especial seria então o limite superior da velocidade da luz no vácuo. Nenhuma variação da velocidade da luz com a frequência foi observada em testes rigorosos, colocando limites rigorosos na massa do fóton. O limite obtido depende do modelo utilizado: se o fóton massivo for descrito pela teoria de Proca, o limite superior experimental para sua massa é de cerca de 10−57 gramas; se a massa do fóton for gerada por um mecanismo de Higgs, o limite superior experimental é menos nítido, m ≤ 10−14 eV/c2 (aproximadamente 2 × 10−47 g).
Outra razão para a velocidade da luz variar com a sua frequência seria a incapacidade da relatividade especial de se aplicar a escalas arbitrariamente pequenas, como previsto por algumas teorias propostas da gravidade quântica. Em 2009, a observação da explosão de raios gama GRB 090510 não encontrou nenhuma evidência de uma dependência da velocidade dos fótons em relação à energia, apoiando restrições rígidas em modelos específicos de quantização do espaço-tempo sobre como esta velocidade é afetada pela energia dos fótons para energias que se aproximam da escala de Planck.
Em um meio
Em um meio, a luz geralmente não se propaga a uma velocidade igual a c; além disso, diferentes tipos de ondas de luz viajarão em velocidades diferentes. A velocidade na qual as cristas e depressões individuais de uma onda plana (uma onda que preenche todo o espaço, com apenas uma frequência) se propagam é chamada de velocidade de fase vp. Um sinal físico com extensão finita (um pulso de luz) viaja a uma velocidade diferente. O envelope geral do pulso viaja na velocidade de grupo vg, e sua primeira parte viaja na velocidade frontal vf< /sub>.
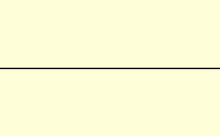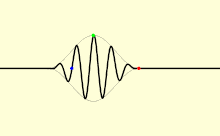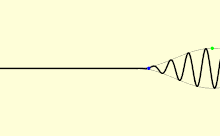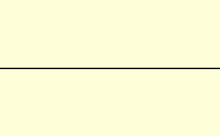
A velocidade de fase é importante para determinar como uma onda de luz viaja através de um material ou de um material para outro. Muitas vezes é representado em termos de um índice de refração. O índice de refração de um material é definido como a razão entre c e a velocidade de fase vp no material: índices de refração maiores indicam índices de refração mais baixos velocidades. O índice de refração de um material pode depender da frequência, intensidade, polarização ou direção de propagação da luz; em muitos casos, porém, pode ser tratada como uma constante dependente do material. O índice de refração do ar é de aproximadamente 1,0003. Meios mais densos, como água, vidro e diamante, têm índices de refração em torno de 1,3, 1,5 e 2,4, respectivamente, para luz visível.
Em materiais exóticos como os condensados de Bose-Einstein próximos do zero absoluto, a velocidade efetiva da luz pode ser de apenas alguns metros por segundo. No entanto, isso representa um atraso na absorção e na re-irradiação entre os átomos, assim como todas as velocidades mais lentas que c nas substâncias materiais. Como um exemplo extremo de "desaceleração' da luz; na matéria, duas equipes independentes de físicos afirmaram ter levado a luz a uma “paralisação completa”; passando-o através de um condensado de Bose-Einstein do elemento rubídio. A descrição popular de luz sendo "parada" nestes experimentos refere-se apenas à luz sendo armazenada nos estados excitados dos átomos, e então reemitida em um momento arbitrariamente posterior, estimulada por um segundo pulso de laser. Durante o tempo em que 'parou', deixou de haver luz. Este tipo de comportamento é geralmente microscopicamente verdadeiro para todos os meios transparentes que são "lentos" A velocidade da luz.
Em materiais transparentes, o índice de refração geralmente é maior que 1, o que significa que a velocidade da fase é menor que c. Em outros materiais, é possível que o índice de refração seja menor que 1 para algumas frequências; em alguns materiais exóticos é até possível que o índice de refração se torne negativo. A exigência de que a causalidade não seja violada implica que as partes real e imaginária da constante dielétrica de qualquer material, correspondendo respectivamente ao índice de refração e ao coeficiente de atenuação, estão ligadas pelas relações de Kramers-Kronig. Em termos práticos, isto significa que num material com índice de refração inferior a 1, a onda será absorvida rapidamente.
Um pulso com diferentes velocidades de grupo e de fase (o que ocorre se a velocidade de fase não for a mesma para todas as frequências do pulso) se espalha ao longo do tempo, um processo conhecido como dispersão. Certos materiais têm uma velocidade de grupo excepcionalmente baixa (ou mesmo zero) para ondas de luz, um fenômeno chamado luz lenta. O oposto, velocidades de grupo superiores a c, foi proposto teoricamente em 1993 e alcançado experimentalmente em 2000. Deveria até ser possível que a velocidade de grupo se tornasse infinita ou negativa, com pulsos viajando instantaneamente ou retrocedendo no tempo.
Nenhuma destas opções permite que a informação seja transmitida mais rapidamente do que c. É impossível transmitir informações com um pulso de luz mais rápido do que a velocidade da parte inicial do pulso (a velocidade frontal). Pode-se mostrar que isto é (sob certas suposições) sempre igual a c.
É possível que uma partícula viaje através de um meio mais rápido que a velocidade de fase da luz nesse meio (mas ainda mais lento que c). Quando uma partícula carregada faz isso em um material dielétrico, é emitido o equivalente eletromagnético de uma onda de choque, conhecida como radiação Cherenkov.
Efeitos práticos da finitude
A velocidade da luz é relevante para as comunicações: o tempo de atraso unidirecional e de ida e volta é maior que zero. Isso se aplica desde escalas pequenas até astronômicas. Por outro lado, algumas técnicas dependem da velocidade finita da luz, por exemplo em medições de distância.
Pequenas escalas
Em computadores, a velocidade da luz impõe um limite na rapidez com que os dados podem ser enviados entre processadores. Se um processador operar a 1 gigahertz, um sinal poderá viajar apenas no máximo cerca de 30 centímetros (1 pé) em um único ciclo de clock. Na prática, essa distância é ainda menor, pois a própria placa de circuito impresso possui um índice de refração e retarda os sinais. Os processadores devem, portanto, ser colocados próximos uns dos outros, assim como os chips de memória, para minimizar as latências de comunicação, e deve-se ter cuidado ao rotear os fios entre eles para garantir a integridade do sinal. Se as frequências do clock continuarem a aumentar, a velocidade da luz poderá eventualmente se tornar um fator limitante para o design interno de chips individuais.
Grandes distâncias na Terra
Considerando que a circunferência equatorial da Terra é de cerca de 40075 km e esse c é cerca de 300000 km/s, o tempo teórico mais curto para uma informação viajar metade do globo ao longo da superfície é de cerca de 67 milissegundos. Quando a luz viaja em fibra óptica (um material transparente), o tempo de trânsito real é mais longo, em parte porque a velocidade da luz é mais lenta em cerca de 35% na fibra óptica, dependendo do seu índice de refração n. As linhas retas são raras nas comunicações globais e o tempo de viagem aumenta quando os sinais passam por interruptores eletrônicos ou regeneradores de sinal.
Embora esta distância seja em grande parte irrelevante para a maioria das aplicações, a latência torna-se importante em áreas como a negociação de alta frequência, onde os traders procuram obter vantagens mínimas entregando as suas negociações às bolsas frações de segundo antes dos outros traders. Por exemplo, os comerciantes têm mudado para comunicações por microondas entre centros comerciais, devido à vantagem que as ondas de rádio que viajam perto da velocidade da luz através do ar têm sobre sinais de fibra óptica comparativamente mais lentos.
Voo espacial e astronomia

Da mesma forma, as comunicações entre a Terra e as naves espaciais não são instantâneas. Há um breve atraso entre a fonte e o receptor, que se torna mais perceptível à medida que as distâncias aumentam. Esse atraso foi significativo para as comunicações entre o controle em solo e a Apollo 8 quando ela se tornou a primeira espaçonave tripulada a orbitar a Lua: para cada pergunta, a estação de controle em solo tinha que esperar pelo menos três segundos para que a resposta chegasse.
O atraso nas comunicações entre a Terra e Marte pode variar entre cinco e vinte minutos, dependendo das posições relativas dos dois planetas. Como consequência disto, se um robô na superfície de Marte encontrasse um problema, os seus controladores humanos só se aperceberiam dele 5–20 minutos mais tarde. Levaria então mais 5–20 minutos para que os comandos viajassem da Terra a Marte.
Receber luz e outros sinais de fontes astronômicas distantes leva muito mais tempo. Por exemplo, são necessários 13 bilhões (13×109) anos para a luz viajar para a Terra a partir de galáxias distantes vistas nas imagens do Hubble Ultra-Deep Field. Essas fotografias, tiradas hoje, capturam imagens das galáxias tal como apareciam há 13 mil milhões de anos, quando o Universo tinha menos de mil milhões de anos. O fato de objetos mais distantes parecerem mais jovens, devido à velocidade finita da luz, permite aos astrônomos inferir a evolução das estrelas, das galáxias e do próprio universo.
As distâncias astronómicas são por vezes expressas em anos-luz, especialmente em publicações e meios de comunicação científicos populares. Um ano-luz é a distância que a luz percorre em um ano juliano, cerca de 9.461 bilhões de quilômetros, 5.879 bilhões de milhas ou 0,3066 parsecs. Em números redondos, um ano-luz equivale a quase 10 trilhões de quilômetros ou quase 6 trilhões de milhas. Proxima Centauri, a estrela mais próxima da Terra depois do Sol, está a cerca de 4,2 anos-luz de distância.
Medição de distância
Os sistemas de radar medem a distância até um alvo pelo tempo que um pulso de onda de rádio leva para retornar à antena do radar depois de ser refletido pelo alvo: a distância até o alvo é metade do tempo de trânsito de ida e volta multiplicado pelo velocidade da luz. Um receptor do Sistema de Posicionamento Global (GPS) mede sua distância até os satélites GPS com base em quanto tempo leva para um sinal de rádio chegar de cada satélite e, a partir dessas distâncias, calcula a posição do receptor. Porque a luz viaja cerca de 300000 quilômetros (186000 mi) em um segundo, essas medições de pequenas frações de segundo devem ser muito precisas. O experimento Lunar Laser Ranging, a astronomia de radar e a Deep Space Network determinam as distâncias até a Lua, planetas e espaçonaves, respectivamente, medindo os tempos de trânsito de ida e volta.
Medição
Existem diferentes maneiras de determinar o valor de c. Uma maneira é medir a velocidade real com que as ondas de luz se propagam, o que pode ser feito em várias configurações astronômicas e baseadas na Terra. Também é possível determinar c a partir de outras leis físicas onde ele aparece, por exemplo, determinando os valores das constantes eletromagnéticas ε0 e μ0 e usando sua relação com c. Historicamente, os resultados mais precisos foram obtidos determinando-se separadamente a frequência e o comprimento de onda de um feixe de luz, com seu produto igualando c. Isso é descrito com mais detalhes na seção "Interferometria" seção abaixo.
Em 1983, o metro foi definido como “o comprimento do caminho percorrido pela luz no vácuo durante um intervalo de tempo de 1⁄299792458 de segundo", fixando o valor da velocidade da luz a 299792458 m/s por definição, conforme descrito abaixo. Consequentemente, medições precisas da velocidade da luz produzem uma realização precisa do medidor, em vez de um valor preciso de c.
Medições astronômicas

O espaço exterior é um cenário conveniente para medir a velocidade da luz devido à sua grande escala e ao vácuo quase perfeito. Normalmente, mede-se o tempo necessário para a luz percorrer alguma distância de referência no Sistema Solar, como o raio da órbita da Terra. Historicamente, tais medições poderiam ser feitas com bastante precisão, em comparação com a precisão com que o comprimento da distância de referência é conhecido em unidades baseadas na Terra.
Ole Christensen Rømer usou uma medição astronômica para fazer a primeira estimativa quantitativa da velocidade da luz no ano de 1676. Quando medido a partir da Terra, os períodos das luas orbitando um planeta distante são mais curtos quando a Terra está se aproximando do planeta do que quando a Terra está se afastando dele. A distância percorrida pela luz do planeta (ou sua lua) até a Terra é menor quando a Terra está no ponto de sua órbita mais próximo de seu planeta do que quando a Terra está no ponto mais distante de sua órbita, a diferença de distância sendo o diâmetro da órbita da Terra em torno do Sol. A mudança observada no período orbital da lua é causada pela diferença no tempo que a luz leva para percorrer a distância mais curta ou mais longa. Rømer observou este efeito para a lua principal mais interna de Júpiter, Io, e deduziu que a luz leva 22 minutos para cruzar o diâmetro da órbita da Terra.

Outro método é usar a aberração da luz, descoberta e explicada por James Bradley no século XVIII. Este efeito resulta da adição vetorial da velocidade da luz que chega de uma fonte distante (como uma estrela) e da velocidade do seu observador (ver diagrama à direita). Um observador em movimento vê assim a luz vindo de uma direção ligeiramente diferente e, consequentemente, vê a fonte numa posição deslocada da sua posição original. Como a direção da velocidade da Terra muda continuamente à medida que a Terra orbita o Sol, este efeito faz com que a posição aparente das estrelas se mova. A partir da diferença angular na posição das estrelas (máximo 20,5 segundos de arco) é possível expressar a velocidade da luz em termos da velocidade da Terra em torno do Sol, que com a duração conhecida de um ano pode ser convertida para a velocidade da Terra em torno do Sol. tempo necessário para viajar do Sol à Terra. Em 1729, Bradley usou esse método para derivar que a luz viajou 10210 vezes mais rápido que a Terra em sua órbita (o número moderno é 10 066 vezes mais rápido) ou, equivalentemente, que a luz levaria 8 minutos e 12 segundos para viajar do Sol à Terra.
Unidade astronômica
Uma unidade astronômica (UA) é aproximadamente a distância média entre a Terra e o Sol. Foi redefinido em 2012 como exatamente 149597870700 m. Anteriormente a UA não se baseava no Sistema Internacional de Unidades, mas sim na força gravitacional exercida pelo Sol no quadro da mecânica clássica. A definição atual utiliza o valor recomendado em metros para a definição anterior da unidade astronômica, que era determinada por medição. Esta redefinição é análoga à do metro e também tem o efeito de fixar a velocidade da luz num valor exacto em unidades astronómicas por segundo (através da velocidade exacta da luz em metros por segundo).
Anteriormente, o inverso de c expresso em segundos por unidade astronômica era medido comparando o tempo que os sinais de rádio levavam para alcançar diferentes espaçonaves no Sol. Sistema, com sua posição calculada a partir dos efeitos gravitacionais do Sol e de vários planetas. Combinando muitas dessas medições, um valor de melhor ajuste para o tempo de luz por unidade de distância poderia ser obtido. Por exemplo, em 2009, a melhor estimativa, aprovada pela União Astronómica Internacional (IAU), foi:
- tempo de luz para distância da unidade: )AU= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =499.004783836(10) s
- c= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0,00200398880410.(4) UA= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =173.144632674(3) UA / dia.
A incerteza relativa nessas medições é de 0,02 partes por bilhão (2×10−11), equivalente à incerteza nas medições de comprimento baseadas na Terra por interferometria. Como o metro é definido como o comprimento percorrido pela luz em um determinado intervalo de tempo, a medição do tempo de luz em termos da definição anterior da unidade astronômica também pode ser interpretada como a medição do comprimento de uma UA (definição antiga) em metros.
Técnicas de tempo de voo

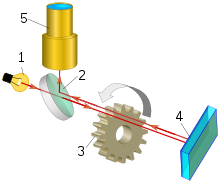
- Fonte de luz
- Espelho semitransparente de corte de feixe
- Disjuntor de roda dentada do feixe de luz
- Espelho remoto
- Tubo telescópico
Um método para medir a velocidade da luz é medir o tempo necessário para a luz viajar até um espelho a uma distância conhecida e voltar. Este é o princípio de funcionamento por trás dos experimentos de Hippolyte Fizeau e Léon Foucault.
A configuração usada por Fizeau consiste em um feixe de luz direcionado a um espelho a 8 quilômetros (5 mi) de distância. No caminho da fonte até o espelho, o feixe passa por uma roda dentada giratória. A uma certa taxa de rotação, o feixe passa por uma abertura na saída e outra na volta, mas em taxas ligeiramente mais altas ou mais baixas, o feixe atinge um dente e não passa pela roda. Conhecendo a distância entre a roda e o espelho, o número de dentes da roda e a taxa de rotação, a velocidade da luz pode ser calculada.
O método de Foucault substitui a roda dentada por um espelho giratório. Como o espelho continua girando enquanto a luz viaja até o espelho distante e volta, a luz é refletida no espelho giratório em um ângulo diferente ao sair e ao voltar. A partir desta diferença de ângulo, a velocidade de rotação conhecida e a distância até o espelho distante, a velocidade da luz pode ser calculada. Foucault utilizou este aparelho para medir a velocidade da luz no ar versus a água, com base numa sugestão de François Arago.
Atualmente, usando osciloscópios com resoluções de tempo inferiores a um nanossegundo, a velocidade da luz pode ser medida diretamente cronometrando o atraso de um pulso de luz de um laser ou de um LED refletido em um espelho. Este método é menos preciso (com erros da ordem de 1%) do que outras técnicas modernas, mas às vezes é usado como experimento de laboratório em aulas de física universitária.
Constantes eletromagnéticas
Uma opção para derivar c que não depende diretamente de uma medição da propagação de ondas eletromagnéticas é usar a relação entre c e a permissividade do vácuo ε0 e permeabilidade ao vácuo μ0 estabelecida pela teoria de Maxwell: c< sup>2 = 1/(ε0μ0). A permissividade do vácuo pode ser determinada medindo a capacitância e as dimensões de um capacitor, enquanto o valor da permeabilidade do vácuo foi historicamente fixado em exatamente < /span>4π×10−7 H⋅m−1 através da definição do ampere. Rosa e Dorsey usaram esse método em 1907 para encontrar um valor de 299710±22 km/s. Seu método dependia de uma unidade padrão de resistência elétrica, o “ohm internacional”, e portanto sua precisão era limitada pela forma como esse padrão era definido.
Ressonância da cavidade

Outra maneira de medir a velocidade da luz é medir independentemente a frequência f e o comprimento de onda λ de uma onda eletromagnética no vácuo. O valor de c pode então ser encontrado usando a relação c = fλ. Uma opção é medir a frequência de ressonância de um ressonador de cavidade. Se as dimensões da cavidade de ressonância também forem conhecidas, estas podem ser usadas para determinar o comprimento de onda da onda. Em 1946, Louis Essen e AC Gordon-Smith estabeleceram a frequência para uma variedade de modos normais de microondas de uma cavidade de microondas de dimensões precisamente conhecidas. As dimensões foram estabelecidas com uma precisão de cerca de ±0,8 μm usando medidores calibrados por interferometria. Como o comprimento de onda dos modos era conhecido pela geometria da cavidade e pela teoria eletromagnética, o conhecimento das frequências associadas possibilitou o cálculo da velocidade da luz.
O resultado de Essen–Gordon-Smith, 299792±9 km/s, foi substancialmente mais preciso do que aqueles encontrados por dados ópticos técnicas. Em 1950, medições repetidas feitas por Essen estabeleceram um resultado de 299792,5±3,0 km/s.
É possível uma demonstração doméstica desta técnica, utilizando um forno micro-ondas e alimentos como marshmallows ou margarina: se o prato giratório for removido para que os alimentos não se movam, ele cozinhará mais rapidamente nos antinodos (os pontos onde a amplitude da onda é maior), onde começará a derreter. A distância entre dois desses pontos é metade do comprimento de onda das microondas; medindo essa distância e multiplicando o comprimento de onda pela frequência de micro-ondas (geralmente exibida na parte traseira do forno, normalmente 2.450 MHz), o valor de c pode ser calculado, "geralmente com menos de Erro de 5%".
Interferometria

A interferometria é outro método para encontrar o comprimento de onda da radiação eletromagnética para determinar a velocidade da luz. Um feixe de luz coerente (por exemplo, de um laser), com uma frequência conhecida (f), é dividido para seguir dois caminhos e depois recombinado. Ajustando o comprimento do caminho enquanto se observa o padrão de interferência e medindo cuidadosamente a mudança no comprimento do caminho, o comprimento de onda da luz (λ) pode ser determinado. A velocidade da luz é então calculada usando a equação c = λf.
Antes do advento da tecnologia laser, fontes de rádio coerentes eram usadas para medições interferométricas da velocidade da luz. A determinação interferométrica do comprimento de onda torna-se menos precisa com o comprimento de onda e os experimentos foram, portanto, limitados em precisão pelo longo comprimento de onda (~4 mm (0,16 pol.)) das ondas de rádio. A precisão pode ser melhorada usando luz com comprimento de onda mais curto, mas torna-se difícil medir diretamente a frequência da luz.
Uma maneira de contornar esse problema é começar com um sinal de baixa frequência cuja frequência possa ser medida com precisão e, a partir desse sinal, sintetizar progressivamente sinais de frequência mais alta, cuja frequência pode então ser vinculada ao sinal original. Um laser pode então ser bloqueado na frequência e seu comprimento de onda pode ser determinado usando interferometria. Essa técnica deveu-se a um grupo do National Bureau of Standards (que mais tarde se tornou o National Institute of Standards and Technology). Eles o usaram em 1972 para medir a velocidade da luz no vácuo com uma incerteza fracionária de 3,5×10−9.
Histórico
Até o início do período moderno, não se sabia se a luz viajava instantaneamente ou a uma velocidade finita muito rápida. O primeiro exame registrado sobre este assunto foi na Grécia antiga. Os antigos gregos, os estudiosos árabes e os cientistas clássicos europeus debateram isto durante muito tempo, até que Rømer forneceu o primeiro cálculo da velocidade da luz. A teoria da relatividade especial de Einstein postula que a velocidade da luz é constante, independentemente do referencial. Desde então, os cientistas têm fornecido medições cada vez mais precisas.
| <1638 | Galileu, lanternas cobertas | inconclusivo | |
| <1667 | Accademia del Cimento, lanternas cobertas | inconclusivo | |
| 1675 | Rømer e Huygens, luas de Júpiter | 220 220) | -27% erro |
| 1729 | James Bradley, aberração da luz | 301) | +0,40% erro |
| 1849 | Hippolyte Fizeau, roda de dentes | 315) | +5.1% erro |
| 1862 | Léon Foucault, espelho rotativo | 298)±500. | -0.60% erro |
| 1907 | Rosa e Dorsey, EM constantes | 299710±30 | -280 ppm erro |
| 1926 | Albert A. Michelson, espelho rotativo | 299796±4 | +12 ppm erro |
| 1950 | Essen e Gordon-Smith, ressonador de cavidade | 299792.5±3.0. | +0,14 ppm erro |
| 1958 | K.D. Froome, interferometria de rádio | 299792.50±0,10 | +0,14 ppm erro |
| 1972 | Evenson et al., interferometria a laser | 299792.4562±0.0011 | -0.006 ppm erro |
| 1983 | 17o CGPM, definição do metro | 299792458 (exacto) | exato, conforme definido |
História antiga
Empédocles (c. 490–430 a.C.) foi o primeiro a propor uma teoria da luz e afirmou que a luz tem uma velocidade finita. Ele sustentou que a luz era algo em movimento e, portanto, deveria levar algum tempo para viajar. Aristóteles argumentou, ao contrário, que “a luz se deve à presença de algo, mas não é um movimento”. Euclides e Ptolomeu avançaram a teoria de Empédocles. teoria da emissão da visão, onde a luz é emitida pelo olho, permitindo assim a visão. Com base nessa teoria, Heron de Alexandria argumentou que a velocidade da luz deve ser infinita porque objetos distantes, como estrelas, aparecem imediatamente ao abrir os olhos.
Os primeiros filósofos islâmicos concordaram inicialmente com a visão aristotélica de que a luz não tinha velocidade de viagem. Em 1021, Alhazen (Ibn al-Haytham) publicou o Livro da Óptica, no qual apresentou uma série de argumentos rejeitando a teoria da emissão da visão em favor da agora aceita teoria da intromissão, na qual a luz se move de um objeto para o olho. Isto levou Alhazen a propor que a luz deve ter uma velocidade finita, e que a velocidade da luz é variável, diminuindo em corpos mais densos. Ele argumentou que a luz é matéria substancial, cuja propagação requer tempo, mesmo que esteja oculto aos sentidos. Também no século 11, Abū Rayhān al-Bīrūnī concordou que a luz tem uma velocidade finita e observou que a velocidade da luz é muito mais rápida que a velocidade do som.
No século XIII, Roger Bacon argumentou que a velocidade da luz no ar não era infinita, usando argumentos filosóficos apoiados pelos escritos de Alhazen e Aristóteles. Na década de 1270, Witelo considerou a possibilidade da luz viajar a velocidade infinita no vácuo, mas desacelerando em corpos mais densos.
No início do século XVII, Johannes Kepler acreditava que a velocidade da luz era infinita, uma vez que o espaço vazio não representava nenhum obstáculo para ela. René Descartes argumentou que se a velocidade da luz fosse finita, o Sol, a Terra e a Lua estariam visivelmente desalinhados durante um eclipse lunar. Embora este argumento falhe quando a aberração da luz é levada em conta, esta última não foi reconhecida até o século seguinte. Como tal desalinhamento não tinha sido observado, Descartes concluiu que a velocidade da luz era infinita. Descartes especulou que se a velocidade da luz fosse finita, todo o seu sistema de filosofia poderia ser demolido. Apesar disso, na sua derivação da lei de Snell, Descartes assumiu que algum tipo de movimento associado à luz era mais rápido em meios mais densos. Pierre de Fermat derivou a lei de Snell usando a suposição oposta: quanto mais denso o meio, mais lenta a luz viajava. Fermat também argumentou a favor de uma velocidade finita da luz.
Primeiras tentativas de medição
Em 1629, Isaac Beeckman propôs um experimento no qual uma pessoa observa o clarão de um canhão refletido em um espelho a cerca de 1,6 km de distância. Em 1638, Galileu Galilei propôs uma experiência, aparentemente alegando tê-la realizado alguns anos antes, para medir a velocidade da luz observando o atraso entre a descoberta de uma lanterna e a sua percepção a alguma distância. Ele não foi capaz de distinguir se a viagem da luz era instantânea ou não, mas concluiu que, se não fosse, deveria ser extraordinariamente rápida. Em 1667, a Accademia del Cimento de Florença informou que havia realizado o experimento de Galileu, com as lanternas separadas por cerca de um quilômetro, mas nenhum atraso foi observado. O atraso real neste experimento teria sido de cerca de 11 microssegundos.
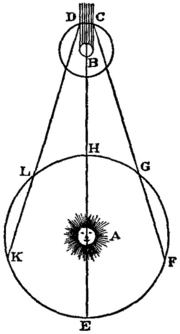
A primeira estimativa quantitativa da velocidade da luz foi feita em 1676 por Ole Rømer. A partir da observação de que os períodos da lua mais interna de Júpiter, Io, pareciam ser mais curtos quando a Terra se aproximava de Júpiter do que quando se afastava dele, ele concluiu que a luz viaja a uma velocidade finita e estimou que a luz leva 22 minutos para cruzar o diâmetro da órbita da Terra. Christiaan Huygens combinou esta estimativa com uma estimativa do diâmetro da órbita da Terra para obter uma estimativa da velocidade da luz de < /span>220000 km/s, o que é 27% menor que o valor real.
Em seu livro Opticks, de 1704, Isaac Newton relatou os cálculos de Rømer sobre a velocidade finita da luz e deu um valor de "sete ou oito minutos" para o tempo que a luz leva para viajar do Sol até a Terra (o valor moderno é 8 minutos e 19 segundos). Newton questionou se as sombras do eclipse de Rømer eram coloridas. Ao ouvir que não, concluiu que as diferentes cores viajavam na mesma velocidade. Em 1729, James Bradley descobriu a aberração estelar. A partir deste efeito, ele determinou que a luz deve viajar 10.210 vezes mais rápido que a Terra em sua órbita (o número moderno é 10.066 vezes mais rápido) ou, equivalentemente, que a luz levaria 8 minutos e 12 segundos para viajar do Sol à Terra.
Conexões com eletromagnetismo
No século XIX, Hippolyte Fizeau desenvolveu um método para determinar a velocidade da luz com base em medições do tempo de voo na Terra e relatou um valor de 315000 km/s. Seu método foi aprimorado por Léon Foucault, que obteve um valor de 298000 km/s em 1862. No ano de 1856, Wilhelm Eduard Weber e Rudolf Kohlrausch mediram a proporção das unidades eletromagnéticas e eletrostáticas de carga, 1/√ε0μ0 , descarregando uma jarra de Leyden, e descobriu que seu valor numérico estava muito próximo da velocidade da luz medida diretamente por Fizeau. No ano seguinte, Gustav Kirchhoff calculou que um sinal eléctrico num fio sem resistência viaja ao longo do fio a esta velocidade.
No início da década de 1860, Maxwell mostrou que, de acordo com a teoria do eletromagnetismo em que estava trabalhando, as ondas eletromagnéticas se propagam no espaço vazio a uma velocidade igual à relação de Weber/Kohlrausch acima, e chamando a atenção para a proximidade numérica desta valor para a velocidade da luz medida por Fizeau, ele propôs que a luz é na verdade uma onda eletromagnética.
"Éter luminoso"

Na época, pensava-se que o espaço vazio era preenchido com um meio de fundo chamado éter luminífero, no qual existia o campo eletromagnético. Alguns físicos pensavam que este éter agia como um quadro de referência preferido para a propagação da luz e, portanto, deveria ser possível medir o movimento da Terra em relação a este meio, medindo a isotropia da velocidade da luz. A partir da década de 1880 foram realizados vários experimentos para tentar detectar esse movimento, sendo o mais famoso o experimento realizado por Albert A. Michelson e Edward W. Morley em 1887. O movimento detectado foi sempre menor que o erro observacional. Experimentos modernos indicam que a velocidade bidirecional da luz é isotrópica (a mesma em todas as direções) com precisão de 6 nanômetros por segundo.
Por causa deste experimento, Hendrik Lorentz propôs que o movimento do aparelho através do éter pode fazer com que o aparelho se contraia ao longo de seu comprimento na direção do movimento, e ele ainda assumiu que a variável de tempo para sistemas em movimento também deve ser alterada de acordo. ("hora local"), o que levou à formulação da transformação de Lorentz. Com base na teoria do éter de Lorentz, Henri Poincaré (1900) mostrou que esta hora local (de primeira ordem em v/c) é indicada por relógios movendo-se no sentido horário. éter, que são sincronizados sob a suposição de velocidade da luz constante. Em 1904, ele especulou que a velocidade da luz poderia ser uma velocidade limitante na dinâmica, desde que todos os pressupostos da teoria de Lorentz fossem confirmados. Em 1905, Poincaré trouxe a teoria do éter de Lorentz para plena concordância observacional com o princípio da relatividade.
Relatividade especial
Em 1905, Einstein postulou desde o início que a velocidade da luz no vácuo, medida por um observador sem aceleração, é independente do movimento da fonte ou do observador. Usando isso e o princípio da relatividade como base, ele derivou a teoria da relatividade especial, na qual a velocidade da luz no vácuo c aparecia como uma constante fundamental, aparecendo também em contextos não relacionados à luz. Isso tornou inútil o conceito de éter estacionário (ao qual Lorentz e Poincaré ainda aderiam) e revolucionou os conceitos de espaço e tempo.
Maior precisão de c e redefinição do medidor e segundo
Na segunda metade do século XX, muito progresso foi feito no aumento da precisão das medições da velocidade da luz, primeiro por técnicas de ressonância de cavidade e mais tarde por técnicas de interferômetro a laser. Estas foram auxiliadas por definições novas e mais precisas de metro e segundo. Em 1950, Louis Essen determinou a velocidade como 299792 .5±3,0 km/s, usando ressonância de cavidade. Este valor foi adotado pela 12ª Assembleia Geral da União Radiocientífica em 1957. Em 1960, o metro foi redefinido em termos do comprimento de onda de uma determinada linha espectral do criptônio-86, e, em 1967, o segundo foi redefinido em termos da frequência de transição hiperfina do estado fundamental do césio-133.
Em 1972, usando o método do interferômetro a laser e as novas definições, um grupo do Departamento Nacional de Padrões dos EUA em Boulder, Colorado, determinou que a velocidade da luz no vácuo era c = 299792456.2±1,1 m/s. Isto era 100 vezes menos incerto do que o valor anteriormente aceito. A incerteza remanescente estava principalmente relacionada com a definição do metro. Como experimentos semelhantes encontraram resultados comparáveis para c, a 15ª Conferência Geral de Pesos e Medidas em 1975 recomendou o uso do valor 299792458 m/s para a velocidade da luz.
Definido como uma constante explícita
Em 1983, a 17ª reunião da Conferência Geral de Pesos e Medidas (CGPM) descobriu que os comprimentos de onda das medições de frequência e um determinado valor para a velocidade da luz são mais reproduzíveis do que o padrão anterior. Eles mantiveram a definição de segundo de 1967, de modo que a frequência hiperfina do césio determinaria agora tanto o segundo quanto o metro. Para fazer isso, eles redefiniram o metro como “o comprimento do caminho percorrido pela luz no vácuo durante um intervalo de tempo de 1/299792458 de um segundo."
Como resultado dessa definição, o valor da velocidade da luz no vácuo é exatamente 299792458 m/s e se tornou uma constante definida no Sistema SI de unidades. Técnicas experimentais aprimoradas que, antes de 1983, teriam medido a velocidade da luz não afetam mais o valor conhecido da velocidade da luz em unidades SI, mas em vez disso permitem uma realização mais precisa do medidor medindo com mais precisão o comprimento de onda do criptônio- 86 e outras fontes de luz.
Em 2011, a CGPM declarou sua intenção de redefinir todas as sete unidades de base do SI usando o que chama de “formulação constante explícita”, onde cada “unidade é definida indiretamente, especificando explicitamente um valor exato”. valor para uma constante fundamental bem reconhecida", como foi feito para a velocidade da luz. Propôs uma redação nova, mas completamente equivalente, para a definição do metro: “O metro, símbolo m, é a unidade de comprimento; sua magnitude é definida fixando o valor numérico da velocidade da luz no vácuo como exatamente 299792458 quando expresso na unidade SI m s−1." Esta foi uma das mudanças incorporadas na redefinição de 2019 das unidades de base do SI, também denominada Novo SI.
