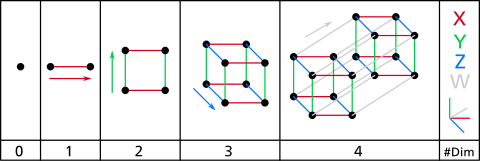Tesserato

A cruz Dalí, uma rede de um tesseract

O tesseract pode ser desdobrado em oito cubos em espaço 3D, assim como o cubo pode ser desdobrado em seis quadrados em espaço 2D.

Em geometria, um tesserato é o análogo quadridimensional do cubo; o tesserato está para o cubo assim como o cubo está para o quadrado. Assim como a superfície do cubo consiste em seis faces quadradas, a hipersuperfície do tesserato consiste em oito células cúbicas. O tesserato é um dos seis 4-polítopos regulares convexos.

O tesseract também é chamado de 8 células, C₈, (regular) octachoron, O quê?, prisma cúbicoe Tetraque. É o quatro dimensões hipercuboou 4-cube como membro da família dimensional de hipercubos ou politopos de medida. Coxeter rotula-o o γ γ 4{displaystyle gamma _{4}} politope. O termo hipercubo sem uma referência de dimensão é frequentemente tratada como sinônimo para este politope específico.

O Oxford English Dictionary rastreia a palavra tesseract ao livro de Charles Howard Hinton de 1888 A New Era of Thought. O termo deriva do grego téssara ( τέσσαρα 'quatro') e do aktís (ἀκτίς 'raio'), referindo-se às quatro arestas de cada vértice para outros vértices. Hinton originalmente soletrava a palavra como tessaract.

Geometria

Como um polítopo regular com três cubos dobrados juntos em cada aresta, possui o símbolo Schläfli {4,3,3} com simetria hiperoctaédrica de ordem 384. Construído como um hiperprisma 4D feito de dois cubos paralelos, pode ser denominado como um símbolo Schläfli composto {4,3} × { }, com ordem de simetria 96. Como um duoprisma 4-4, um produto cartesiano de dois quadrados, pode ser nomeado por um símbolo Schläfli composto {4}×{4}, com ordem de simetria 64. Como um ortótopo, pode ser representado pelo símbolo Schläfli composto { } × { } × { } × { } ou { }⁴, com ordem de simetria 16.

Como cada vértice de um tesserato é adjacente a quatro arestas, a figura do vértice do tesserato é um tetraedro regular. O politopo dual do tesserato é o de 16 células com o símbolo Schläfli {3,3,4}, com o qual pode ser combinado para formar o composto de tesserato e 16 células.

Cada borda de um tesserato regular tem o mesmo comprimento. Isso é interessante ao usar tesseracts como base para uma topologia de rede para vincular vários processadores em computação paralela: a distância entre dois nós é de no máximo 4 e há muitos caminhos diferentes para permitir o balanceamento de peso.

Coordenadas

O tesserato padrão no espaço 4 euclidiano é dado como o envoltório convexo dos pontos (±1, ±1, ±1, ±1). Ou seja, é composto pelos pontos:

((x1,x2,x3,x4)∈ ∈ R4:- Sim. - Sim. 1≤ ≤ xEu...≤ ≤ 1?{displaystyle {(x_{1},x_{2},x_{3},x_{4})in mathbb {R} ^{4},:,-1leq x_{i}leq 1}}

Neste referencial cartesiano, o tesserato tem raio 2 e é limitado por oito hiperplanos (x_i = ±1). Cada par de hiperplanos não paralelos se cruzam para formar 24 faces quadradas em um tesserato. Três cubos e três quadrados se cruzam em cada aresta. Existem quatro cubos, seis quadrados e quatro arestas que se encontram em cada vértice. Ao todo, consiste em 8 cubos, 24 quadrados, 32 arestas e 16 vértices.

Rede

Um desdobramento de um politopo é chamado de rede. Existem 261 redes distintas do tesseract. Os desdobramentos do tesserato podem ser contados mapeando as redes para árvores pareadas (uma árvore junto com uma correspondência perfeita em seu complemento).

Construção

Uma animação do deslocamento em dimensões

A construção de hipercubos pode ser imaginada da seguinte forma:

• 1-dimensional: Dois pontos A e B podem ser conectados para se tornar uma linha, dando um novo segmento de linha AB.
• 2-dimensional: Dois segmentos de linha paralela AB e CD separados por uma distância de AB podem ser conectados para se tornar um quadrado, com os cantos marcados como ABCD.
• 3-dimensional: Dois quadrados paralelos ABCD e EFGH separados por uma distância de AB podem ser conectados para se tornar um cubo, com os cantos marcados como ABCDEFGH.
• 4-dimensional: Dois cubos paralelos ABCDEFGH e IJKLMNOP separados por uma distância de AB podem ser conectados para se tornar um tesseract, com os cantos marcados como ABCDEFGHIJKLMNOP. No entanto, este posicionamento paralelo de dois cubos de tal forma que seus 8 pares correspondentes de vértices são cada um separados por uma distância de AB só pode ser alcançado em um espaço de 4 ou mais dimensões.

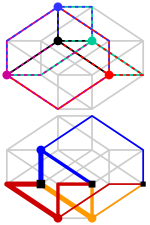
As 8 células do tesserato podem ser consideradas (de três maneiras diferentes) como dois anéis interligados de quatro cubos.

O tesserato pode ser decomposto em 4 politopos menores. É o casco convexo do composto de dois demitesseratos (16 células). Também pode ser triangulado em simplices de 4 dimensões (5 células irregulares) que compartilham seus vértices com o tesserato. Sabe-se que existem 92487256 dessas triangulações e que o menor número de simplices de 4 dimensões em qualquer um deles é 16.

A dissecção do tesseract em instâncias de seu simplex característico (uma ortoesquema particular com diagrama de Coxeter ) é a construção direta mais básica do tesseract possível. O característica 5-célula do 4-cubo é uma região fundamental do grupo de simetria de definição do tesseract, o grupo que gera os politopos B4. O tesseract característica simplex diretamente gera o tesseract através das ações do grupo, refletindo-se em suas próprias facetas amarradas (sua paredes de espelho).

Simetria equilátera radial

O raio maior (do centro ao vértice) do tesserato é igual ao comprimento da aresta; assim, sua diagonal através do centro (vértice a vértice oposto) é de 2 comprimentos de aresta. Apenas alguns politopos uniformes têm essa propriedade, incluindo o tesserato quadridimensional e de 24 células, o cuboctaedro tridimensional e o hexágono bidimensional. Em particular, o tesserato é o único hipercubo (além de um ponto 0-dimensional) que é radialmente equilátero. O maior diâmetro vértice a vértice de um hipercubo n dimensional de comprimento de aresta unitário é √n, então para o quadrado é √2, para o cubo é √3, e apenas para o tesseract é √4, exatamente 2 comprimentos de borda.

Em coordenadas de raio unitário, as coordenadas do tesserato de comprimento de aresta unitário são:

(1/2, ±1/2, ±1/2, ±1/2)

Fórmulas

Prova sem palavras que um grafo hipercubo não é planejado usando teoremas de Kuratowski ou Wagner e encontrando ou KK₅ (top) ou KK_3,3 (bottom) subgrafias

Para um tesseract com comprimento lateral s:

• Hipervolume: H. H. H.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =S4Não. H=s^{4}}
• Volume de superfície: SV= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =8S3[displaystyle SV=8s^{3}}
• Diagonal da cara: D2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2SNão. Não.
• diagonal da célula: D3= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =3SNão. - Não. Não.
• 4-espaço diagonal: D4= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2SNão. Não.

Como configuração

Esta matriz de configuração representa o tesseract. As linhas e colunas correspondem a vértices, arestas, faces e células. Os números diagonais dizem quantos de cada elemento ocorrem em todo o tesserato. Os números não diagonais dizem quantos elementos da coluna ocorrem dentro ou no elemento da linha. Por exemplo, o 2 na primeira coluna da segunda linha indica que existem 2 vértices em (isto é, nos extremos de) cada aresta; o 4 na segunda coluna da primeira linha indica que 4 arestas se encontram em cada vértice.

Não.16.464232334424.281268]{displaystyle {begin{bmatrix}{begin{matrix}16&4&6&42&32&3&3\4&4&24&28&12&6&8end{matrix}}end{bmatrix}}}

Projeções

É possível projetar tesseratos em espaços tridimensionais e bidimensionais, da mesma forma que projetar um cubo em um espaço bidimensional.

Os envelopes de projeção paralelos do tesseract (cada célula é desenhada com diferentes faces de cor, as células invertidas são desenredadas)

O dodecaedro rhombic forma o casco convexo do vértice-primeiro projeto paralelo do tesseract. O número de vértices nas camadas desta projeção é de 1 4 6 4 1 - a quarta linha no triângulo de Pascal.

A projeção paralela célula primeiro do tesserato no espaço tridimensional tem um envelope cúbico. As células mais próximas e mais distantes são projetadas no cubo, e as seis células restantes são projetadas nas seis faces quadradas do cubo.

A projeção paralela face primeiro do tesserato no espaço tridimensional tem um envelope cúbico. Dois pares de células se projetam para as metades superior e inferior deste envelope, e as quatro células restantes se projetam para as faces laterais.

A projeção paralela borda primeiro do tesserato no espaço tridimensional tem um envelope na forma de um prisma hexagonal. Seis células se projetam em prismas rômbicos, que são dispostos no prisma hexagonal de maneira análoga a como as faces do cubo 3D se projetam em seis losangos em um envelope hexagonal sob a projeção do primeiro vértice. As duas células restantes se projetam nas bases do prisma.

A projeção paralela primeiro vértice do tesserato no espaço tridimensional tem um envelope dodecaédrico rômbico. Dois vértices do tesserato são projetados para a origem. Existem exatamente duas maneiras de dissecar um dodecaedro rômbico em quatro romboedros congruentes, dando um total de oito romboedros possíveis, cada um um cubo projetado do tesserato. Essa projeção também é aquela com volume máximo. Um conjunto de vetores de projeção são u=(1,1,-1,-1), v=(-1,1,-1,1), w=(1,-1,-1,1).

Animação mostrando cada cubo individual dentro do B₄ Projeção do plano de Coxeter do tesseract

Projeções ortográficos

Avião de Coxeador	B4	B4 --- A3	A3
Gráfico
Simetria dihedral	[8]	[4]	[4]
Avião de Coxeador	Outros	B3 / D4 / A2	B2 / D3
Gráfico
Simetria dihedral	[2]	[6]	[4]

Uma projeção 3D de um tesseract realizando uma rotação simples sobre um plano em espaço 4-dimensional. O avião bisecta a figura da frente esquerda para trás-direita e superior para baixo.

Uma projeção 3D de um tesseract realizando uma rotação dupla sobre dois planos ortogonais no espaço 4-dimensional.

3D Projecção de três tesseracts com e sem rostos

Perspectiva com eliminação de volume oculto. O canto vermelho é o mais próximo em 4D e tem 4 células cúbicas que se encontram ao seu redor.

O tetraedro forma o casco convexo da projeção central centrada no vértice do tesseract. Quatro de 8 células cúbicos são mostradas. O vértice 16 é projetado para infinito e as quatro bordas para ele não são mostradas.

Projeção estereográfica (Edges são projetados para a 3 esferas)

Projeção 3D estereoscópica de um tesseract (vista paralela)

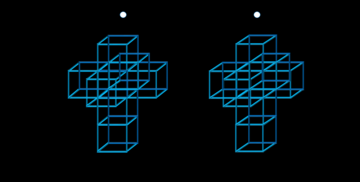Hipercube Desarmed 3D estereoscópico 3D

Tesselação

O tesserato, como todos os hipercubos, pavimenta o espaço euclidiano. O favo de mel tesserático autodual que consiste em 4 tesseratos em torno de cada face tem o símbolo Schläfli {4,3,3,4}. Portanto, o tesserato tem um ângulo diedro de 90°.

A simetria radial equilátera do tesserato torna sua tesselação a única rede cúbica regular centrada no corpo de esferas de tamanho igual, em qualquer número de dimensões.

Polítopos e favos de mel relacionados

O tesserato é o quarto em uma série de hipercubos:

Projeções ortográficos de polígono petie

Segmento de linha	Praça	Cubo	4-cube	5-cube	6-cubo	7-cubo	8-cubo

O tesserato (8 células) é o terceiro na sequência de 6 4 polítopos regulares convexos (em ordem de tamanho e complexidade).

Convexo regular 4-polytops
Grupo de simetria	A4	B4		F4	H4
Nome	5-célula Hipertetraedro 5-ponto	16 células Hiper-octahedron 8 pontos	8 células Hipercubo 16 pontos	24-célula 24 pontos	600 células Hiper-icosaedro 120 pontos	120 células Hiper-dodecaedro 600 pontos
Símbolo de Schläfli	3, 3, 3	3, 3, 4	(4, 3, 3)	3, 4, 3	3, 3, 5	5, 3, 3
Espelhos de Coxeter
Dihedrals de espelho	D/3 D/3 D/3 D/2 D/2 D/2	D/3 D/3 D/4 D/2 D/2 D/2	D/4 D/3 D/3 D/2 D/2 D/2	D/3 D/4 D/3 D/2 D/2 D/2	D/3 D/3 D/5 D/2 D/2 D/2	D/5 D/3 D/3 D/2 D/2 D/2
Gráfico
Versículos	5 tetrahedral	8 octahedral	16 tetrahedral	24 cúmplices	120 icosahedral	600 tetrahedral
Bordas	10 triangulares	24 quadrados	32 triangulares	96 triangulares	720 pentagonal	1200 triangular
Caras	10 triângulos	32 triângulos	24 quadrados	96 triângulos	1200 triângulos	Pentágonos de 720
Células	5 anos de idade	16 anos de idade	8 cubos	24 octahedra	600 tetraedros	120 dólares
Tori!	1 5-tetraedro	2 8-tetraedro	2 4-cube	4 6-octahedron	20 30-tetraedro	12 10-docaedron
Inscrição	120 em 120 células	675 em 120 células	2 16 células	3 8 células	25 24 células	10 600 células
Grandes polígonos		2 quadrados x 3	4 retângulos x 4	4 hexágonos x 4	12 decagons x 6	100 hexágonos irregulares x 4
Poligões de Petrie	1 pentágono	1 octógono	2 octógonos	2 dodecagons	4 30-gons	20 30-gons
Raio longo	1Não. 1	1Não. 1	1Não. 1	1Não. 1	1Não. 1	1Não. 1
Comprimento da borda	52? ? 1.581- Não. {5}{2}}}approx 1.581}	2? ? 1.414{displaystyle {sqrt {2}}approx 1.414}	1Não. 1	1Não. 1	1φ φ ? ? 0.618{displaystyle {tfrac {1}{phi }}approx 0.618}	1φ φ 22? ? 0,270{displaystyle {tfrac {1}{phi ^{2}{sqrt {2}}approx 0.270}
Raio curto	14Não. Não.	12Não. Não.	12Não. Não.	12? ? 007- Não. {1}{2}}}approx 0.707}	φ φ 48? ? 0,926- Não. {phi ^{4}}{8}}}approx 0.926}	φ φ 48? ? 0,926- Não. {phi ^{4}}{8}}}approx 0.926}
Área	10.(538)? ? 10.825{displaystyle 10left({tfrac) (5 {3}}}{8}}right)approx 10.825}	32(34)? ? 27.713{displaystyle 32left({sqrt {tfrac {3}{4}}}right)approx 27.713}	24.Não.	96(316.)? ? 41.569{displaystyle 96left({sqrt {tfrac {3}{16}}}right)approx 41.569}	1200(34φ φ 2)? ? 198.48{displaystyle 1200left({tfrac {sqrt {3}}{4phi ^{2}}}right)approx 198.48}	720(25+10.58φ φ 4)? ? 90.366{displaystyle 720left({tfrac {sqrt {25+10{sqrt} {5}}{8phi ^{4}}}right)approx 90.366}
Volume	5(5524.)? ? 2.329{displaystyle 5left({tfrac) (5 {5}}}{24}}right)approx 2.329}	16.(13)? ? 5.333{displaystyle 16left({tfrac {1}{3}}right)approx 5.333}	8Não. 8	24.(23)? ? 11.314(em inglês) {2}}{3}}right)approx 11.314}	600(212φ φ 3)? ? 16.693{displaystyle 600left({tfrac) {sqrt {2}}{12phi ^{3}}}right)approx 16.693}	120(15+754φ φ 68)? ? 18.118{displaystyle 120left({tfrac {15+7{sqrt {5}}}{4phi ^{6}{sqrt {8}}right)approx 18.118}
4-Conteúdo	524.(52)4? ? 0,146{displaystyle {tfrac {sqrt {5}}{24}}left({tfrac {sqrt} {5}}{2}}right)^{4}approx 0.146}	23? ? 0.667{displaystyle {tfrac {2}{3}}approx 0.667}	1Não. 1	2Não. 2	Curto× × Vol.4? ? 3.863{displaystyle {tfrac {{text{Short}}times {text{Vol}}}{4}}approx 3.863}	Curto× × Vol.4? ? 4.193{displaystyle {tfrac {{text{Short}}times {text{Vol}}}{4}}approx 4.193}

Como um duoprisma uniforme, o tesserato existe em uma sequência de duoprismas uniformes: {p}×{4}.

O tesserato regular, junto com o de 16 células, existe em um conjunto de 15 4 politopos uniformes com a mesma simetria. O tesserato {4,3,3} existe em uma sequência de 4-polítopos regulares e favos de mel, {p,3,3} com figuras de vértices tetraédricos, {3,3}. O tesserato também está em uma sequência regular de 4 politopos e favos de mel, {4,3,p} com células cúbicas.

Ortogonal	Perspectiva
4(4)2, com 16 vértices e 8 4 bordas, com as 8 4 bordas mostradas aqui como 4 vermelho e 4 quadrados azuis

O politope complexo regular ₄(4)₂, , in C2{displaystyle mathbb {C} ^{2}} tem uma representação real como um tesseract ou 4-4 duoprism no espaço 4-dimensional. ₄(4)₂ tem 16 vértices e 8 4 bordas. Sua simetria é ₄[4]₂Ordem 32. Ele também tem uma construção de simetria inferior, ou ₄Não.₄{}, com simetria ₄[2]₄Ordem 16. Esta é a simetria se as 4 bordas vermelhas e azuis são consideradas distintas.

Na cultura popular

Desde sua descoberta, os hipercubos quadridimensionais têm sido um tema popular na arte, arquitetura e ficção científica. Exemplos notáveis incluem:

• "And He Built a Crooked House", história de ficção científica de Robert Heinlein de 1940, com um edifício na forma de um hipercubo de quatro dimensões. Este e o "The No-Sided Professor" de Martin Gardner, publicado em 1946, estão entre os primeiros na ficção científica a apresentar aos leitores a banda Moebius, a garrafa Klein e o hipercubo (tesseract).
• Crucificação (Corpus Hypercubus), uma pintura a óleo de 1954 de Salvador Dalí com um hipercubo de quatro dimensões desdobrado em uma cruz latina tridimensional.
• O Grande Arche, um monumento e edifício perto de Paris, França, concluído em 1989. De acordo com o engenheiro do monumento, Erik Reitzel, o Grande Arche foi projetado para se assemelhar à projeção de um hipercubo.
• Fez., um jogo de vídeo onde se joga um personagem que pode ver além das duas dimensões que outros personagens podem ver, e deve usar esta capacidade de resolver quebra-cabeças de plataforma. Características "Dot", um tesseract que ajuda o jogador a navegar pelo mundo e diz como usar habilidades, ajustando o tema de ver além da percepção humana do espaço dimensional conhecido.

A palavra tesserato foi posteriormente adotada para vários outros usos na cultura popular, inclusive como um dispositivo de enredo em obras de ficção científica, muitas vezes com pouca ou nenhuma conexão com o hipercubo quadridimensional. Veja Tesseract (desambiguação).