Teoria do caos

Uma parcela do atrator Lorenz para valores R = 28, σ = 10, b) = 8/3

Uma animação de um pêndulo duplo-rod em uma energia intermediária mostrando comportamento caótico. Começar o pêndulo de uma condição inicial ligeiramente diferente resultaria em uma trajetória muito diferente. O pêndulo duplo é um dos sistemas dinâmicos mais simples com soluções caóticas.

Teoria do caos é uma área interdisciplinar de estudo científico e ramo da matemática focado em padrões subjacentes e leis determinísticas de sistemas dinâmicos que são altamente sensíveis a condições iniciais e que já foram pensados para ter estados completamente aleatórios de desordem e irregularidades. A teoria do caos afirma que, dentro da aparente aleatoriedade dos sistemas complexos caóticos, existem padrões subjacentes, interconexão, loops de feedback constantes, repetição, autossimilaridade, fractais e auto-organização. O efeito borboleta, um princípio subjacente do caos, descreve como uma pequena mudança em um estado de um sistema não linear determinístico pode resultar em grandes diferenças em um estado posterior (o que significa que há uma dependência sensível das condições iniciais). Uma metáfora para esse comportamento é que o bater de asas de uma borboleta no Brasil pode causar um tornado no Texas.

Pequenas diferenças nas condições iniciais, como as devidas a erros nas medições ou devido a erros de arredondamento na computação numérica, podem gerar resultados amplamente divergentes para tais sistemas dinâmicos, tornando a previsão de longo prazo de seu comportamento impossível em geral. Isso pode acontecer mesmo que esses sistemas sejam determinísticos, ou seja, seu comportamento futuro segue uma evolução única e é totalmente determinado por suas condições iniciais, sem elementos aleatórios envolvidos. Em outras palavras, a natureza determinística desses sistemas não os torna previsíveis. Este comportamento é conhecido como caos determinístico, ou simplesmente caos. A teoria foi resumida por Edward Lorenz como:

Caos: Quando o presente determina o futuro, mas o presente aproximado não determina aproximadamente o futuro.

O comportamento caótico existe em muitos sistemas naturais, incluindo fluxo de fluidos, irregularidades de batimentos cardíacos, tempo e clima. Também ocorre espontaneamente em alguns sistemas com componentes artificiais, como o tráfego rodoviário. Este comportamento pode ser estudado através da análise de um modelo matemático caótico, ou através de técnicas analíticas como plotagens de recorrência e mapas de Poincaré. A teoria do caos tem aplicações em uma variedade de disciplinas, incluindo meteorologia, antropologia, sociologia, ciência ambiental, ciência da computação, engenharia, economia, ecologia e gestão de crises pandêmicas. A teoria formou a base para campos de estudo como sistemas dinâmicos complexos, teoria da borda do caos e processos de automontagem.

Introdução

A teoria do caos diz respeito a sistemas determinísticos cujo comportamento pode, em princípio, ser previsto. Sistemas caóticos são previsíveis por um tempo e então 'aparecem' tornar-se aleatório. A quantidade de tempo para a qual o comportamento de um sistema caótico pode ser efetivamente previsto depende de três coisas: quanta incerteza pode ser tolerada na previsão, com que precisão seu estado atual pode ser medido e uma escala de tempo que depende da dinâmica do sistema. sistema, chamado de tempo de Lyapunov. Alguns exemplos de tempos de Lyapunov são: circuitos elétricos caóticos, cerca de 1 milissegundo; sistemas meteorológicos, alguns dias (não comprovado); o sistema solar interno, 4 a 5 milhões de anos. Em sistemas caóticos, a incerteza em uma previsão aumenta exponencialmente com o tempo decorrido. Assim, matematicamente, duplicar o tempo de previsão mais do que o quadrado da incerteza proporcional na previsão. Isso significa, na prática, que uma previsão significativa não pode ser feita em um intervalo de mais de duas ou três vezes o tempo de Lyapunov. Quando previsões significativas não podem ser feitas, o sistema parece aleatório.

A teoria do caos é um método de análise qualitativa e quantitativa para investigar o comportamento de sistemas dinâmicos que não podem ser explicados e previstos por relacionamentos de dados únicos, mas devem ser explicados e previstos por relacionamentos de dados completos e contínuos.

Dinâmica caótica

O mapa definido por x → 4 x (1 x) e Sim. →x + Sim. mod 1 exibe sensibilidade às posições x iniciais. Aqui, duas séries de x e Sim. valores divergem marcadamente ao longo do tempo de uma pequena diferença inicial.

No uso comum, "caos" significa "um estado de desordem". No entanto, na teoria do caos, o termo é definido com mais precisão. Embora não exista uma definição matemática universalmente aceita de caos, uma definição comumente usada, originalmente formulada por Robert L. Devaney, diz que para classificar um sistema dinâmico como caótico, ele deve ter as seguintes propriedades:

1. deve ser sensível às condições iniciais,
2. deve ser topologicamente transitivo,
3. deve ter órbitas periódicas densas.

Em alguns casos, as duas últimas propriedades acima mostraram realmente implicar em sensibilidade às condições iniciais. No caso de tempo discreto, isso é verdade para todos os mapas contínuos em espaços métricos. Nesses casos, embora muitas vezes seja a propriedade mais significativa na prática, a "sensibilidade às condições iniciais" não precisa ser declarado na definição.

Se a atenção estiver restrita a intervalos, a segunda propriedade implica nas outras duas. Uma alternativa e uma definição geralmente mais fraca de caos usa apenas as duas primeiras propriedades da lista acima.

Sensibilidade às condições iniciais

Equações de Lorenz usadas para gerar parcelas para a variável y. As condições iniciais para x e zangão. foram mantidos iguais, mas aqueles para Sim. foram alterados 1.001, 1.000. e 1.000.01. Os valores para ? ? - Sim., σ σ - Sim. e β β - Sim. eles/elas/vocês 45.92, 16. e 4 respectivamente. Como pode ser visto do gráfico, mesmo a menor diferença nos valores iniciais causa mudanças significativas após cerca de 12 segundos de evolução nos três casos. Este é um exemplo de dependência sensível das condições iniciais.

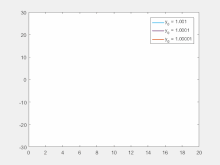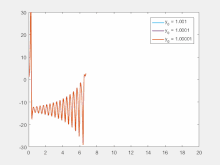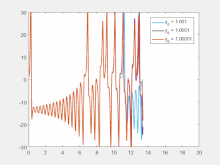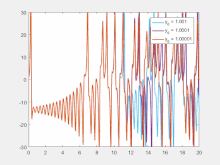
Sensibilidade às condições iniciais significa que cada ponto em um sistema caótico é arbitrariamente aproximado por outros pontos que têm caminhos ou trajetórias futuras significativamente diferentes. Assim, uma alteração ou perturbação arbitrariamente pequena da trajetória atual pode levar a um comportamento futuro significativamente diferente.

A sensibilidade às condições iniciais é popularmente conhecida como "efeito borboleta", assim chamada por causa do título de um artigo dado por Edward Lorenz em 1972 à Associação Americana para o Avanço da Ciência em Washington, D.C., intitulado Previsibilidade: o bater de asas de uma borboleta no Brasil desencadeou um tornado no Texas?. A asa batendo representa uma pequena mudança na condição inicial do sistema, que causa uma cadeia de eventos que impede a previsibilidade de fenômenos de grande escala. Se a borboleta não tivesse batido as asas, a trajetória do sistema como um todo poderia ter sido muito diferente.

Conforme sugerido no livro de Lorenz intitulado "The Essence of Chaos", publicado em 1993, "a dependência sensível pode servir como uma definição de caos". No mesmo livro, Lorenz definiu o efeito borboleta como: "O fenômeno em que uma pequena alteração no estado de um sistema dinâmico fará com que os estados subsequentes sejam muito diferentes dos estados que se seguiriam sem a alteração. " A definição acima é consistente com a dependência sensível das soluções nas condições iniciais (SDIC). Um modelo de esqui idealizado foi desenvolvido para ilustrar a sensibilidade dos caminhos variáveis no tempo para as posições iniciais. Um horizonte de previsibilidade pode ser determinado antes do início do SDIC (ou seja, antes de separações significativas de trajetórias próximas iniciais).

Uma consequência da sensibilidade às condições iniciais é que, se começarmos com uma quantidade limitada de informações sobre o sistema (como geralmente é o caso na prática), depois de um certo tempo, o sistema não será mais previsível. Isso é mais prevalente no caso do clima, que geralmente é previsível apenas cerca de uma semana à frente. Isso não significa que não se possa afirmar nada sobre eventos distantes no futuro - apenas que algumas restrições no sistema estão presentes. Por exemplo, sabemos que a temperatura da superfície da Terra não atingirá naturalmente 100 °C (212 °F) ou cairá abaixo de −130 °C (−202 °F) na Terra (durante a era geológica atual), mas não podemos prever exatamente qual dia terá a temperatura mais quente do ano.

Em termos mais matemáticos, o expoente Lyapunov mede a sensibilidade às condições iniciais, na forma de taxa de divergência exponencial das condições iniciais perturbadas. Mais especificamente, dado duas trajetórias iniciais no espaço de fase que são infinitamente próximas, com separação inicial δ δ Z.0{displaystyle delta mathbf] {Z} _{0}}, as duas trajetórias acabam divergindo a uma taxa dada por

|δ δ Z.())|? ? eλ λ )|δ δ Z.0|,{displaystyle |delta mathbf {Z} (t)|approx e^{lambda t}|delta mathbf {Z} _{0}|,}

Onde? )Não. é a hora e λ λ - Sim. é o expoente Lyapunov. A taxa de separação depende da orientação do vetor de separação inicial, de modo que todo o espectro de expoentes Lyapunov pode existir. O número de expoentes de Lyapunov é igual ao número de dimensões do espaço de fase, embora seja comum apenas referir-se ao maior. Por exemplo, o expoente máximo Lyapunov (MLE) é mais frequentemente usado, porque determina a previsibilidade geral do sistema. Um MLE positivo é geralmente tomado como uma indicação de que o sistema é caótico.

Além da propriedade acima, também existem outras propriedades relacionadas à sensibilidade das condições iniciais. Isso inclui, por exemplo, mistura teórica de medida (conforme discutido na teoria ergódica) e propriedades de um sistema K.

Não periodicidade

Um sistema caótico pode ter sequências de valores para a variável em evolução que se repetem exatamente, dando um comportamento periódico a partir de qualquer ponto dessa sequência. No entanto, tais sequências periódicas são repelentes em vez de atrativas, o que significa que se a variável em evolução estiver fora da sequência, por mais próxima que seja, ela não entrará na sequência e, de fato, divergirá dela. Assim, para quase todas as condições iniciais, a variável evolui caoticamente com comportamento não periódico.

Mistura topológica

Seis iterações de um conjunto de estados Não.x,Sim.][x,y] passou pelo mapa logístico. O primeiro iterado (azul) é a condição inicial, que essencialmente forma um círculo. A animação mostra o primeiro à sexta iteração das condições iniciais circulares. Pode ser visto que mistura ocorre à medida que avançamos em iterações. A sexta iteração mostra que os pontos estão quase completamente espalhados no espaço de fase. Se tivéssemos progredido mais em iterações, a mistura teria sido homogênea e irreversível. O mapa logístico tem equação xk+1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =4xk(1- Sim. - Sim. xk)Não. x_{k+1}=4x_{k}(1-x_{k})}. Expandir o espaço estatal do mapa logístico em duas dimensões, um segundo estado, Sim.- Sim., foi criado como Sim.k+1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =xk+Sim.kNão. y_{k+1}=x_{k}+y_{k}}, se <math alttext="{displaystyle x_{k}+y_{k}xk+Sim.k<1Não. x_{k}+y_{k}<1}<img alt="{displaystyle x_{k}+y_{k} e Sim.k+1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =xk+Sim.k- Sim. - Sim. 1Não. y_{k+1}=x_{k}+y_{k}-1} caso contrário.

O mapa definido por x → 4 x (1 x) e Sim. →x + Sim. mod 1 também exibe mistura topológica. Aqui, a região azul é transformada pela dinâmica primeiro para a região roxa, depois para as regiões rosa e vermelha, e eventualmente para uma nuvem de linhas verticais espalhadas pelo espaço.

A mistura topológica (ou a condição mais fraca de transitividade topológica) significa que o sistema evolui ao longo do tempo, de modo que qualquer região ou conjunto aberto de seu espaço de fase eventualmente se sobreponha a qualquer outra região. Este conceito matemático de "mistura" corresponde à intuição padrão, e a mistura de corantes ou fluidos coloridos é um exemplo de sistema caótico.

A mistura topológica é frequentemente omitida dos relatos populares de caos, que igualam o caos apenas com a sensibilidade às condições iniciais. No entanto, a dependência sensível apenas das condições iniciais não gera caos. Por exemplo, considere o sistema dinâmico simples produzido pela duplicação repetida de um valor inicial. Este sistema tem uma dependência sensível das condições iniciais em todos os lugares, uma vez que qualquer par de pontos próximos eventualmente se torna amplamente separado. No entanto, este exemplo não possui mistura topológica e, portanto, não possui caos. Na verdade, tem um comportamento extremamente simples: todos os pontos, exceto 0, tendem ao infinito positivo ou negativo.

Transitividade topológica

Um mapa f:X→ → X{displaystyle f:Xto X} é dito ser topologicamente transitivo se para qualquer par de conjuntos abertos não vazios U,V? ? X{displaystyle U,Vsubset X}, existe 0}" xmlns="http://www.w3.org/1998/Math/MathML">k>0- Sim.0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/27b3af208b148139eefc03f0f80fa94c38c5af45" style="vertical-align: -0.338ex; width:5.472ex; height:2.176ex;"/> tal que fk(U)─ ─ V≠ ≠ ∅ ∅ {displaystyle f^{k}(U)cap Vneq emptyset }. A transitividade topológica é uma versão mais fraca da mistura topológica. Intuitivamente, se um mapa é topologicamente transitivo então dado um ponto x e uma região V, existe um ponto Sim. perto x cuja órbita passa V. Isso implica que é impossível decompor o sistema em dois conjuntos abertos.

Um importante teorema relacionado é o Teorema da Transitividade de Birkhoff. É fácil ver que a existência de uma órbita densa implica transitividade topológica. O Teorema da Transitividade de Birkhoff afirma que se X é um segundo espaço métrico completo e contável, então a transitividade topológica implica a existência de um conjunto denso de pontos em X que possuem órbitas densas.

Densidade de órbitas periódicas

Para um sistema caótico ter órbitas periódicas densas significa que cada ponto no espaço é abordado arbitrariamente por órbitas periódicas. O mapa logístico unidimensional definido por x → 4 x (1 x) é um dos sistemas mais simples com densidade de órbitas periódicas. Por exemplo, 5- Sim. - Sim. 58Não. (5- {5}}}{8}→ 5+58Não. (5+ {5}}}{8}→ 5- Sim. - Sim. 58Não. (5- {5}}}{8} (ou aproximadamente 0.3454915 → 0.9045085 → 0.3454915) é uma órbita (instável) do período 2, e órbitas semelhantes existem por períodos 4, 8, 16, etc. (indevido, para todos os períodos especificados pelo teorema de Sharkovskii).

O teorema de Sharkovskii é a base da prova de Li e Yorke (1975) de que qualquer sistema unidimensional contínuo que exibe um ciclo regular de período três também exibirá ciclos regulares de todos os outros comprimentos, bem como completamente órbitas caóticas.

Atratores estranhos

O atrator Lorenz exibe comportamento caótico. Estas duas parcelas demonstram dependência sensível das condições iniciais dentro da região do espaço de fase ocupado pelo atrator.

Alguns sistemas dinâmicos, como o mapa logístico unidimensional definido por x → 4 x (1 – x), são caóticos em todos os lugares, mas em muitos casos o comportamento caótico é encontrado apenas em um subconjunto do espaço de fase. Os casos de maior interesse surgem quando o comportamento caótico ocorre em um atrator, pois um grande conjunto de condições iniciais leva a órbitas que convergem para essa região caótica.

Uma maneira fácil de visualizar um atrator caótico é começar com um ponto na bacia de atração do atrator e simplesmente traçar sua órbita subsequente. Devido à condição de transitividade topológica, é provável que isso produza uma imagem de todo o atrator final e, de fato, ambas as órbitas mostradas na figura à direita fornecem uma imagem da forma geral do atrator de Lorenz. Este atrator resulta de um modelo tridimensional simples do sistema meteorológico de Lorenz. O atractor de Lorenz é talvez um dos diagramas de sistemas caóticos mais conhecidos, provavelmente por ser não só um dos primeiros, mas também um dos mais complexos, e como tal dá origem a um padrão muito interessante que, com uma pouca imaginação, parece as asas de uma borboleta.

Ao contrário dos atratores de ponto fixo e dos ciclos limite, os atratores que surgem de sistemas caóticos, conhecidos como atratores estranhos, possuem grande detalhe e complexidade. Atratores estranhos ocorrem tanto em sistemas dinâmicos contínuos (como o sistema de Lorenz) quanto em alguns sistemas discretos (como o mapa de Hénon). Outros sistemas dinâmicos discretos possuem uma estrutura repelente chamada conjunto de Julia, que se forma na fronteira entre bacias de atração de pontos fixos. Os conjuntos de Julia podem ser considerados repelentes estranhos. Tanto os atratores estranhos quanto os conjuntos de Julia geralmente têm uma estrutura fractal, e a dimensão fractal pode ser calculada para eles.

Atratores coexistentes

Atratores caóticos e não caóticos coexistentes dentro do modelo generalizado Lorenz. Há 128 órbitas em cores diferentes, começando com diferentes condições iniciais para tempo sem dimensão entre 0,625 e 5 e um parâmetro de aquecimento r = 680. As órbitas caóticas retornam recorrentemente perto do ponto de sela na origem. As órbitas nonchaóticas eventualmente se aproximam de um dos dois pontos críticos estáveis, como mostrado com grandes pontos azuis. As órbitas caóticas e nonchaóticas ocupam diferentes regiões de atração dentro do espaço de fase.

Em contraste com soluções caóticas de tipo único, estudos recentes usando modelos de Lorenz enfatizaram a importância de considerar vários tipos de soluções. Por exemplo, a coexistência de caótico e não caótico pode aparecer dentro do mesmo modelo (por exemplo, o sistema de pêndulo duplo) usando as mesmas configurações de modelagem, mas diferentes condições iniciais. As descobertas da coexistência de atratores, obtidas a partir dos modelos clássicos e generalizados de Lorenz, sugeriram uma visão revisada de que “todo o clima possui uma natureza dupla de caos e ordem com previsibilidade distinta”, em contraste com a visão convencional de “o clima é caótico”.

Complexidade mínima de um sistema caótico

Diagrama de bifurcação do mapa logístico x → R x (1 x). Cada fatia vertical mostra o atrator para um valor específico de R. O diagrama exibe o período de duplicação como R aumenta, eventualmente produzindo o caos. Pontos mais escuros são visitados com mais frequência.

Sistemas caóticos discretos, como o mapa logístico, podem exibir estranhos atratores, seja qual for a sua dimensão. Universalidade de mapas unidimensionais com maxima parabólico e constantes de Feigenbaum δ δ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =4.669201...{displaystyle delta =4.669201...},α α = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2.502907...{displaystyle alpha =2.502907...} é bem visível com mapa proposto como um brinquedo modelo para dinâmica laser discreta: x→ → Gx(1- Sim. - Sim. )umnh(x))(x)}, Onde? xNão. significa amplitude de campo elétrico, GNão. G. é ganho a laser como parâmetro de bifurcação. O aumento gradual de GNão. G. em intervalo Não.0,∞ ∞ )[0,infty]} mudanças dinâmicas de regular para caótico com qualitativamente o mesmo diagrama de bifurcação como aqueles para mapa logístico.

Em contraste, para sistemas dinâmicos contínuos, o teorema de Poincaré–Bendixson mostra que um atrator estranho só pode surgir em três ou mais dimensões. Sistemas lineares de dimensão finita nunca são caóticos; para um sistema dinâmico exibir comportamento caótico, ele deve ser não linear ou de dimensão infinita.

O teorema de Poincaré–Bendixson afirma que uma equação diferencial bidimensional tem um comportamento muito regular. O atrator de Lorenz discutido abaixo é gerado por um sistema de três equações diferenciais, tais como:

DxD)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =σ σ Sim.- Sim. - Sim. σ σ x,DSim.D)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =? ? x- Sim. - Sim. xzangão.- Sim. - Sim. Sim.,Dzangão.D)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =xSim.- Sim. - Sim. β β zangão..- Sim. t}}&=sigma y-sigma x,\{frac {mathrm {d} y}{mathrm {d} t}}&=rho x-xz-y,{frac {mathrm {d} z}{mathrm {d} t}}&=xy-beta z.end{aligned}}}

Onde? xNão., Sim.- Sim.e zangão.Não. compõem o estado do sistema, )Não. é tempo, e σ σ - Sim., ? ? - Sim., β β - Sim. são os parâmetros do sistema. Cinco dos termos do lado direito são lineares, enquanto dois são quadráticos; um total de sete termos. Outro atrator caótico bem conhecido é gerado pelas equações de Rössler, que têm apenas um termo não linear de sete. Sprott encontrou um sistema tridimensional com apenas cinco termos, que tinha apenas um termo não linear, que exibe o caos para certos valores de parâmetros. Zhang e Heidel mostraram que, pelo menos para sistemas quadráticos dissipativos e conservadores, sistemas quadráticos tridimensionais com apenas três ou quatro termos no lado direito não podem apresentar comportamento caótico. A razão é, simplesmente, que as soluções para tais sistemas são assintóticas a uma superfície bidimensional e, portanto, as soluções são bem comportadas.

Enquanto o teorema de Poincaré-Bendixson mostra que um sistema dinâmico contínuo no plano euclidiano não pode ser caótico, sistemas contínuos bidimensionais com geometria não euclidiana podem exibir comportamento caótico. Talvez surpreendentemente, o caos também pode ocorrer em sistemas lineares, desde que sejam infinitos dimensionais. Uma teoria do caos linear está sendo desenvolvida em um ramo da análise matemática conhecida como análise funcional.

O conjunto elegante acima de três equações diferenciais ordinárias foi referido como o modelo tridimensional de Lorenz. Desde 1963, os modelos Lorenz de alta dimensão foram desenvolvidos em vários estudos para examinar o impacto de um aumento do grau de não linearidade, bem como seu efeito coletivo com aquecimento e dissipações, na estabilidade da solução.

mapas dimensionais infinitos

A generalização direta dos mapas discretos acoplados baseia-se na integral de convolução que media a interação entre mapas distribuídos espacialmente: ? ? n+1(R→ → ,))= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ KK(R→ → - Sim. - Sim. R→ → ,,))fNão.? ? n(R→ → ,,))]DR→ → ,{displaystyle psi _{n+1}({vec {r}},t)=int K({vec {r}}-{vec {r}}^{,},t)f[psi _{n}({vec {r}}^{,},t)]d{vec {r}}^{,}}}},

onde o kernel KK(R→ → - Sim. - Sim. R→ → ,,)){displaystyle K({vec {r}}-{vec {r}}^{,},t)} é propagador derivado como função verde de um sistema físico relevante, fNão.? ? n(R→ → ,))]{displaystyle f[psi _{n}({vec {r}},t)]} pode ser mapa logístico semelhante ? ? → → G? ? Não.1- Sim. - Sim. Tanh⁡ ⁡ (? ? )]{displaystyle psi rightarrow Gpsi [1-tanh(psi)]} ou mapa complexo. Para exemplos de mapas complexos o conjunto Julia fNão.? ? ]= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =? ? 2{displaystyle f[psi ]=psi ^{2}} ou mapa de Ikeda ? ? n+1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =A+B? ? neEu...(|? ? n|2+C){displaystyle psi _{n+1}=A+Bpsi _{n}e^{i(|psi _{n}|^{2}+C)}} pode servir. Quando problemas de propagação de ondas à distância L= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =c)Não. Não. com comprimento de onda λ λ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2D D /k{displaystyle lambda =2pi /k} são considerados o kernel KKNão. pode ter uma forma de função verde para a equação de Schrödinger:.

KK(R→ → - Sim. - Sim. R→ → ,,L)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...kexp⁡ ⁡ Não.Eu...kL]2D D Lexp⁡ ⁡ Não.Eu...k|R→ → - Sim. - Sim. R→ → ,|22L]{displaystyle K({vec {r}}-{vec {r}}^{,},L)={frac {ikexp[ikL]}{2pi L}}exp[{frac {ik|{vec {r}}-{vec {r}}^{,}|^{2}}{2L}}}.

Sistemas idiotas

Na física, jerk é a terceira derivada da posição, em relação ao tempo. Assim, equações diferenciais da forma

JJ(x...,x" " ,x:: ,x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0{displaystyle Jleft({overset) {...}{x}},{ddot {x}},{dot {x}},xright)=0}

às vezes são chamadas de equações idiotas. Foi demonstrado que uma equação jerk, que é equivalente a um sistema de três equações diferenciais não lineares ordinárias de primeira ordem, é, em certo sentido, o cenário mínimo para soluções que apresentam comportamento caótico. Isso motiva o interesse matemático em sistemas idiotas. Sistemas envolvendo uma quarta ou superior derivada são chamados de sistemas hyperjerk.

O comportamento de um sistema jerk é descrito por uma equação jerk, e para certas equações jerk, circuitos eletrônicos simples podem modelar soluções. Esses circuitos são conhecidos como circuitos jerk.

Uma das propriedades mais interessantes de circuitos idiotas é a possibilidade de comportamento caótico. De fato, certos sistemas chaóticos bem conhecidos, como o atrator Lorenz e o mapa de Rössler, são descritos convencionalmente como um sistema de três equações diferenciais de primeira ordem que podem combinar em uma única (embora bastante complicada) equação idiota. Outro exemplo de uma equação idiota com não linearidade na magnitude de xNão. é:

D3xD)3+AD2xD)2+DxD)- Sim. - Sim. |x|+1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0.- Não. t^{3}}}+ A{frac {mathrm {d} ^{2}x}{mathrm {d} t^{2}}}+{frac {mathrm {d} x}{mathrm {d} t}}-|x|+1=0.}

Aqui, a é um parâmetro ajustável. Esta equação possui uma solução caótica para a = 3/5 e pode ser implementada com o seguinte circuito jerk; A não linearidade necessária é provocada pelos dois diodos:

No circuito acima, todos os resistores são de igual valor, exceto RA= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R/A= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =5R/3Não. R_{A}=R/A=5R/3}, e todos os capacitores são de tamanho igual. A frequência dominante é 1/2D D RC{displaystyle 1/2pi RC. A saída de op amp 0 corresponderá à variável x, a saída de 1 corresponde ao primeiro derivado de x e a saída de 2 corresponde ao segundo derivado.

circuitos semelhantes requerem apenas um diodo ou nenhum diodos.

Veja também o conhecido circuito de Chua, uma base para geradores de números aleatórios verdadeiros caóticos. A facilidade de construção do circuito o tornou um exemplo onipresente do mundo real de um sistema caótico.

Ordem espontânea

Sob as condições certas, o caos evolui espontaneamente para um padrão de bloqueio. No modelo Kuramoto, quatro condições são suficientes para produzir sincronização em um sistema caótico. Exemplos incluem a oscilação acoplada de Christiaan Huygens ' Pêndulos, vaga -lumes, neurônios, ressonância de Londres Millennium Bridge e grandes matrizes de junções de Josephson.

HISTÓRIA

Barnsley fern criou usando o jogo de caos. As formas naturais (fernos, nuvens, montanhas, etc.) podem ser recriadas através de um sistema de função iterada (IFS).

Um dos primeiros defensores da teoria do caos foi Henri Poincaré. Na década de 1880, enquanto estudava o problema dos três corpos, ele descobriu que pode haver órbitas não periódicas, mas que não aumentam continuamente nem se aproximam de um ponto fixo. Em 1898, Jacques Hadamard publicou um estudo influente do movimento caótico de uma partícula livre deslizando sem atrito em uma superfície de curvatura negativa constante, chamada de "Hadamard's billiards". Hadamard conseguiu mostrar que todas as trajetórias são instáveis, pois todas as trajetórias das partículas divergem exponencialmente umas das outras, com um expoente de Lyapunov positivo.

A teoria do caos começou no campo da teoria ergódica. Estudos posteriores, também sobre o tema de equações diferenciais não lineares, foram realizados por George David Birkhoff, Andrey Nikolaevich Kolmogorov, Mary Lucy Cartwright e John Edensor Littlewood, e Stephen Smale. Com exceção de Smale, esses estudos foram todos inspirados diretamente pela física: o problema dos três corpos no caso de Birkhoff, turbulência e problemas astronômicos no caso de Kolmogorov, e engenharia de rádio no caso de Cartwright e Littlewood. Embora o movimento planetário caótico não tenha sido observado, os experimentalistas encontraram turbulência no movimento do fluido e oscilação não periódica em circuitos de rádio sem o benefício de uma teoria para explicar o que estavam vendo.

Apesar dos insights iniciais na primeira metade do século XX, a teoria do caos tornou-se formalizada como tal apenas depois de meados do século, quando se tornou evidente para alguns cientistas que a teoria linear, a teoria do sistema predominante na época, simplesmente não poderia explicar o comportamento observado de certos experimentos como o do mapa logístico. O que havia sido atribuído à imprecisão da medida e ao simples "ruído" foi considerado pelos teóricos do caos como um componente integral dos sistemas estudados. Em 1959, Chirikov propôs um critério para o surgimento do caos clássico em sistemas hamiltonianos (critério de Chirikov). Ele aplicou esse critério para explicar alguns resultados experimentais sobre confinamento de plasma em armadilhas de espelho aberto. Esta é considerada a primeira teoria física do caos, que conseguiu explicar um experimento concreto. E o próprio Chirikov é considerado um pioneiro no caos clássico e quântico.

O principal catalisador para o desenvolvimento da teoria do caos foi o computador eletrônico. Grande parte da matemática da teoria do caos envolve a iteração repetida de fórmulas matemáticas simples, o que seria impraticável de se fazer à mão. Os computadores eletrônicos tornaram práticos esses cálculos repetidos, enquanto figuras e imagens possibilitaram a visualização desses sistemas. Como estudante de pós-graduação no laboratório de Chihiro Hayashi na Universidade de Kyoto, Yoshisuke Ueda estava fazendo experiências com computadores analógicos e notou, em 27 de novembro de 1961, o que chamou de "fenômenos de transição aleatória". No entanto, seu orientador não concordou com suas conclusões na época e não permitiu que ele relatasse suas descobertas até 1970.

Turbulência no vórtice de ponta de uma asa de avião. Estudos do ponto crítico além do qual um sistema cria turbulência foram importantes para a teoria do caos, analisados por exemplo pelo físico soviético Lev Landau, que desenvolveu a teoria da turbulência de Landau-Hopf. David Ruelle e Floris Takens mais tarde previram, contra Landau, que a turbulência do fluido poderia desenvolver através de um estranho atrator, um conceito principal de teoria do caos.

Edward Lorenz foi um dos primeiros pioneiros da teoria. Seu interesse pelo caos surgiu acidentalmente por meio de seu trabalho sobre previsão do tempo em 1961. Lorenz e sua colaboradora Ellen Fetter estavam usando um computador digital simples, um Royal McBee LGP-30, para executar simulações do tempo. Eles queriam ver uma sequência de dados novamente e, para economizar tempo, iniciaram a simulação no meio de seu curso. Eles fizeram isso inserindo uma impressão dos dados que correspondiam às condições no meio da simulação original. Para sua surpresa, o tempo que a máquina começou a prever era completamente diferente do cálculo anterior. Eles rastrearam isso até a impressão do computador. O computador funcionou com precisão de 6 dígitos, mas a impressão arredondou as variáveis para um número de 3 dígitos, portanto, um valor como 0,506127 foi impresso como 0,506. Essa diferença é pequena e o consenso na época seria que não deveria ter efeito prático. No entanto, Lorenz descobriu que pequenas mudanças nas condições iniciais produziam grandes mudanças no resultado a longo prazo. A descoberta de Lorenz, que deu nome aos atratores de Lorenz, mostrou que mesmo a modelagem atmosférica detalhada não pode, em geral, fazer previsões meteorológicas precisas a longo prazo.

Em 1963, Benoit Mandelbrot, estudando a teoria da informação, descobriu que o ruído em muitos fenômenos (incluindo preços de ações e circuitos telefônicos) era modelado como um conjunto de Cantor, um conjunto de pontos com rugosidade e detalhes infinitos.;Efeito Noah" (no qual podem ocorrer mudanças descontínuas repentinas) e o "efeito Joseph" (no qual a persistência de um valor pode ocorrer por um tempo, mas mudar repentinamente depois). Em 1967, ele publicou "How long is the coast of Britain? Auto-semelhança estatística e dimensão fracionária, mostrando que o comprimento de uma linha costeira varia com a escala do instrumento de medição, assemelha-se a si mesmo em todas as escalas e é infinito em comprimento para um dispositivo de medição infinitesimalmente pequeno. Argumentando que um novelo de barbante aparece como um ponto quando visto de longe (0-dimensional), uma bola quando visto de perto (3-dimensional), ou um fio curvo (1-dimensional), ele argumentou que as dimensões de um objeto são relativos ao observador e podem ser fracionários. Um objeto cuja irregularidade é constante em diferentes escalas ("autossimilaridade") é um fractal (exemplos incluem a esponja de Menger, a junta de Sierpiński e a curva de Koch ou floco de neve, que é infinitamente longo, mas abrange um espaço finito e tem uma dimensão fractal de cerca de 1,2619). Em 1982, Mandelbrot publicou The Fractal Geometry of Nature, que se tornou um clássico da teoria do caos.

Em dezembro de 1977, a Academia de Ciências de Nova York organizou o primeiro simpósio sobre o caos, com a presença de David Ruelle, Robert May, James A. Yorke (cunhador do termo "caos" usado na matemática), Robert Shaw e o meteorologista Edward Lorenz. No ano seguinte, Pierre Coullet e Charles Tresser publicaram "Itérations d'endomorphismes et groupe de renormalisation", e o artigo de Mitchell Feigenbaum "Quantitative Universality for a Class of Nonlinear Transformations" finalmente apareceu em um jornal, após 3 anos de rejeições do árbitro. Assim, Feigenbaum (1975) e Coullet & Tresser (1978) descobriu a universalidade no caos, permitindo a aplicação da teoria do caos a muitos fenômenos diferentes.

Em 1979, Albert J. Libchaber, durante um simpósio organizado em Aspen por Pierre Hohenberg, apresentou sua observação experimental da cascata de bifurcação que leva ao caos e à turbulência em sistemas de convecção Rayleigh-Bénard. Ele recebeu o Prêmio Wolf de Física em 1986 junto com Mitchell J. Feigenbaum por suas conquistas inspiradoras.

Em 1986, a Academia de Ciências de Nova York co-organizou com o Instituto Nacional de Saúde Mental e o Escritório de Pesquisa Naval a primeira conferência importante sobre o caos na biologia e na medicina. Lá, Bernardo Huberman apresentou um modelo matemático da disfunção do eye tracking em pessoas com esquizofrenia. Isso levou a uma renovação da fisiologia na década de 1980 por meio da aplicação da teoria do caos, por exemplo, no estudo dos ciclos cardíacos patológicos.

Em 1987, Per Bak, Chao Tang e Kurt Wiesenfeld publicaram um artigo em Physical Review Letters descrevendo pela primeira vez a criticalidade auto-organizada (SOC), considerada um dos mecanismos pelos quais a complexidade surge na natureza.

Ao lado de abordagens largamente baseadas em laboratório, como a pilha de areia de Bak–Tang–Wiesenfeld, muitas outras investigações se concentraram em sistemas naturais ou sociais de grande escala que são conhecidos (ou suspeitos) de exibir comportamento invariante à escala. Embora essas abordagens nem sempre tenham sido bem-vindas (pelo menos inicialmente) pelos especialistas nos assuntos examinados, o SOC se estabeleceu como um forte candidato para explicar uma série de fenômenos naturais, incluindo terremotos (que, muito antes da descoberta do SOC, eram conhecidos como uma fonte de comportamento invariante à escala, como a lei de Gutenberg-Richter descrevendo a distribuição estatística de tamanhos de terremoto e a lei de Omori descrevendo a frequência de tremores secundários), explosões solares, flutuações em sistemas econômicos, como mercados financeiros (referências a SOC são comum em econofísica), formação da paisagem, incêndios florestais, deslizamentos de terra, epidemias e evolução biológica (onde o SOC foi invocado, por exemplo, como o mecanismo dinâmico por trás da teoria dos "equilíbrios pontuados" apresentada por Niles Eldredge e Stephen Jay Gould). Dadas as implicações de uma distribuição sem escala de tamanhos de eventos, alguns pesquisadores sugeriram que outro fenômeno que deveria ser considerado um exemplo de SOC é a ocorrência de guerras. Essas investigações de SOC incluíram tentativas de modelagem (seja desenvolvendo novos modelos ou adaptando os existentes às especificidades de um determinado sistema natural) e extensa análise de dados para determinar a existência e/ou características de leis de escala natural.

No mesmo ano, James Gleick publicou Chaos: Making a New Science, que se tornou um best-seller e introduziu os princípios gerais da teoria do caos, bem como sua história, para o público em geral. Inicialmente domínio de poucos indivíduos isolados, a teoria do caos emergiu progressivamente como uma disciplina transdisciplinar e institucional, principalmente sob o nome de análise de sistemas não lineares. Aludindo ao conceito de mudança de paradigma de Thomas Kuhn exposto em A Estrutura das Revoluções Científicas (1962), muitos "caólogos" (como alguns se descreveram) afirmaram que esta nova teoria era um exemplo de tal mudança, uma tese sustentada por Gleick.

A disponibilidade de computadores mais baratos e poderosos amplia a aplicabilidade da teoria do caos. Atualmente, a teoria do caos continua sendo uma área ativa de pesquisa, envolvendo muitas disciplinas diferentes, como matemática, topologia, física, sistemas sociais, modelagem populacional, biologia, meteorologia, astrofísica, teoria da informação, neurociência computacional, gerenciamento de crises pandêmicas, etc.

Uma analogia popular, mas imprecisa, para o caos

A dependência sensível das condições iniciais (ou seja, efeito borboleta) foi ilustrada usando o seguinte folclore:

“Por falta de um prego, perdeu-se o sapato.

Por falta de uma ferradura, perdeu-se o cavalo.

Por falta de um cavalo, perdeu-se o cavaleiro.

Por falta de um cavaleiro, a batalha foi perdida.

Por falta de uma batalha, o reino foi perdido.

E tudo por falta de um prego de ferradura”.

Com base no exposto, muitas pessoas acreditam erroneamente que o impacto de uma pequena perturbação inicial aumenta monotonicamente com o tempo e que qualquer pequena perturbação pode eventualmente produzir um grande impacto nas integrações numéricas. No entanto, em 2008, Lorenz afirmou que não sentia que este versículo descrevia o verdadeiro caos, mas que ilustrava melhor o fenômeno mais simples da instabilidade e que o versículo sugere implicitamente que pequenos eventos subsequentes não reverterão o resultado (Lorenz, 2008). Com base na análise, o versículo indica apenas divergência, não limitação. A delimitação é importante para o tamanho finito de um padrão de borboleta.

Aplicativos

Uma concha têxtil conus, semelhante à regra 30, um autômato celular com comportamento caótico.

Embora a teoria do caos tenha nascido da observação de padrões climáticos, ela se tornou aplicável a uma variedade de outras situações. Algumas áreas que se beneficiam da teoria do caos hoje são geologia, matemática, biologia, ciência da computação, economia, engenharia, finanças, meteorologia, filosofia, antropologia, física, política, dinâmica populacional e robótica. Algumas categorias estão listadas abaixo com exemplos, mas esta não é uma lista abrangente, pois novos aplicativos estão aparecendo.

Criptografia

A teoria do caos tem sido usada por muitos anos em criptografia. Nas últimas décadas, o caos e a dinâmica não linear foram usados no projeto de centenas de primitivas criptográficas. Esses algoritmos incluem algoritmos de criptografia de imagem, funções de hash, geradores de números pseudo-aleatórios seguros, cifras de fluxo, marca d'água e esteganografia. A maioria desses algoritmos são baseados em mapas caóticos unimodais e uma grande parte desses algoritmos usa os parâmetros de controle e a condição inicial dos mapas caóticos como suas chaves. De uma perspectiva mais ampla, sem perda de generalidade, as semelhanças entre os mapas caóticos e os sistemas criptográficos é a principal motivação para o projeto de algoritmos criptográficos baseados no caos. Um tipo de criptografia, chave secreta ou chave simétrica, depende de difusão e confusão, que é bem modelada pela teoria do caos. Outro tipo de computação, a computação de DNA, quando combinada com a teoria do caos, oferece uma maneira de criptografar imagens e outras informações. Muitos dos algoritmos criptográficos DNA-Chaos provaram não ser seguros, ou a técnica aplicada é sugerida como não sendo eficiente.

Robótica

A robótica é outra área que recentemente se beneficiou da teoria do caos. Em vez de robôs agindo em um tipo de refinamento de tentativa e erro para interagir com seu ambiente, a teoria do caos foi usada para construir um modelo preditivo. A dinâmica caótica foi exibida por robôs bípedes passivos.

Biologia

Há mais de cem anos, os biólogos acompanham as populações de diferentes espécies com modelos populacionais. A maioria dos modelos é contínua, mas recentemente os cientistas conseguiram implementar modelos caóticos em certas populações. Por exemplo, um estudo sobre modelos de linces canadenses mostrou que houve um comportamento caótico no crescimento populacional. O caos também pode ser encontrado em sistemas ecológicos, como a hidrologia. Embora um modelo caótico para hidrologia tenha suas deficiências, ainda há muito a aprender ao observar os dados pelas lentes da teoria do caos. Outra aplicação biológica é encontrada na cardiotocografia. A vigilância fetal é um equilíbrio delicado entre a obtenção de informações precisas e, ao mesmo tempo, o menos invasiva possível. Melhores modelos de sinais de alerta de hipóxia fetal podem ser obtidos por meio de modelagem caótica.

Como aponta Perry, a modelagem de séries temporais caóticas em ecologia é ajudada pela restrição. Há sempre uma dificuldade potencial em distinguir o caos real do caos que está apenas no modelo. Portanto, tanto a restrição no modelo quanto os dados duplicados da série temporal para comparação serão úteis para restringir o modelo a algo próximo da realidade, por exemplo, Perry & Wall 1984. A coevolução gene a gene algumas vezes mostra uma dinâmica caótica nas frequências alélicas. Adicionar variáveis exagera isso: o caos é mais comum em modelos que incorporam variáveis adicionais para refletir facetas adicionais de populações reais. O próprio Robert M. May fez alguns desses estudos fundamentais de coevolução de culturas, e isso, por sua vez, ajudou a moldar todo o campo. Mesmo para um ambiente estável, a simples combinação de uma cultura e um patógeno pode resultar em oscilações quasi-periódicas ou caóticas na população de patógenos.

Economia

É possível que os modelos econômicos também possam ser melhorados por meio da aplicação da teoria do caos, mas prever a saúde de um sistema econômico e quais fatores mais o influenciam é uma tarefa extremamente complexa. Os sistemas econômicos e financeiros são fundamentalmente diferentes daqueles nas ciências naturais clássicas, uma vez que os primeiros são inerentemente estocásticos por natureza, pois resultam das interações das pessoas e, portanto, é improvável que modelos determinísticos puros forneçam representações precisas dos dados. A literatura empírica que testa o caos em economia e finanças apresenta resultados muito mistos, em parte devido à confusão entre testes específicos para o caos e testes mais gerais para relações não lineares.

O caos pode ser encontrado na economia por meio da análise de quantificação de recorrência. De fato, Orlando et al. por meio do chamado índice de correlação de quantificação de recorrência foram capazes de detectar mudanças ocultas em séries temporais. Em seguida, a mesma técnica foi empregada para detectar transições de fases laminares (regulares) para turbulentas (caóticas), bem como diferenças entre variáveis macroeconômicas e destacar características ocultas da dinâmica econômica. Por fim, o caos pode ajudar na modelagem de como a economia opera, bem como na incorporação de choques devido a eventos externos como o COVID-19.

Outras áreas

Em química, prever a solubilidade do gás é essencial para a fabricação de polímeros, mas os modelos que usam otimização de enxame de partículas (PSO) tendem a convergir para os pontos errados. Uma versão aprimorada do PSO foi criada com a introdução do caos, que evita que as simulações fiquem paralisadas. Na mecânica celeste, especialmente ao observar asteróides, a aplicação da teoria do caos leva a melhores previsões sobre quando esses objetos se aproximarão da Terra e de outros planetas. Quatro das cinco luas de Plutão giram caoticamente. Na física quântica e na engenharia elétrica, o estudo de grandes arranjos de junções de Josephson se beneficiou muito da teoria do caos. Mais perto de casa, as minas de carvão sempre foram lugares perigosos onde vazamentos frequentes de gás natural causam muitas mortes. Até recentemente, não havia uma maneira confiável de prever quando eles ocorreriam. Mas esses vazamentos de gás têm tendências caóticas que, quando devidamente modeladas, podem ser previstas com bastante precisão.

A teoria do caos pode ser aplicada fora das ciências naturais, mas historicamente quase todos esses estudos sofreram com a falta de reprodutibilidade; fraca validade externa; e/ou falta de atenção à validação cruzada, resultando em baixa precisão preditiva (se a previsão fora da amostra tiver sido tentada). Glass e Mandell e Selz descobriram que nenhum estudo de EEG até agora indicou a presença de atratores estranhos ou outros sinais de comportamento caótico.

Os pesquisadores continuaram a aplicar a teoria do caos à psicologia. Por exemplo, ao modelar o comportamento do grupo em que membros heterogêneos podem se comportar como se compartilhassem em diferentes graus o que na teoria de Wilfred Bion é uma suposição básica, os pesquisadores descobriram que a dinâmica do grupo é o resultado da dinâmica individual dos membros.: cada indivíduo reproduz a dinâmica do grupo em uma escala diferente, e o comportamento caótico do grupo se reflete em cada membro.

Redington e Reidbord (1992) tentaram demonstrar que o coração humano pode apresentar características caóticas. Eles monitoraram as mudanças nos intervalos entre os batimentos cardíacos de uma única paciente em psicoterapia enquanto ela passava por períodos de intensidade emocional variável durante uma sessão de terapia. Os resultados foram reconhecidamente inconclusivos. Não só havia ambiguidades nos vários gráficos que os autores produziram para supostamente mostrar evidências de dinâmica caótica (análise espectral, trajetória de fase e gráficos de autocorrelação), mas também quando eles tentaram calcular um expoente de Lyapunov como confirmação mais definitiva do comportamento caótico, o os autores descobriram que não podiam fazê-lo de forma confiável.

Em seu artigo de 1995, Metcalf e Allen sustentaram que descobriram no comportamento animal um padrão de duplicação de período que leva ao caos. Os autores examinaram uma resposta bem conhecida chamada polidipsia induzida por esquema, pela qual um animal privado de comida por certos períodos de tempo bebe quantidades incomuns de água quando a comida é finalmente apresentada. O parâmetro de controle (r) operando aqui foi a duração do intervalo entre as mamadas, uma vez retomadas. Os autores tiveram o cuidado de testar um grande número de animais e de incluir muitas repetições, e planejaram seu experimento de modo a descartar a probabilidade de mudanças nos padrões de resposta serem causadas por diferentes pontos de partida para r.

As séries temporais e os gráficos de primeiro atraso fornecem o melhor suporte para as reivindicações feitas, mostrando uma marcha bastante clara da periodicidade para a irregularidade à medida que os tempos de alimentação foram aumentados. Os vários gráficos de trajetória de fase e análises espectrais, por outro lado, não combinam bem o suficiente com os outros gráficos ou com a teoria geral para levar inexoravelmente a um diagnóstico caótico. Por exemplo, as trajetórias de fase não mostram uma progressão definida em direção a uma complexidade cada vez maior (e afastando-se da periodicidade); o processo parece bastante confuso. Além disso, onde Metcalf e Allen viram períodos de dois e seis em seus gráficos espectrais, há espaço para interpretações alternativas. Toda essa ambigüidade exige alguma explicação post-hoc serpentina para mostrar que os resultados se encaixam em um modelo caótico.

Ao adaptar um modelo de aconselhamento de carreira para incluir uma interpretação caótica da relação entre os funcionários e o mercado de trabalho, Amundson e Bright descobriram que sugestões melhores podem ser feitas para pessoas que lutam com decisões de carreira. As organizações modernas são cada vez mais vistas como sistemas adaptativos complexos abertos com estruturas não lineares naturais fundamentais, sujeitas a forças internas e externas que podem contribuir para o caos. Por exemplo, a construção de equipes e o desenvolvimento de grupos estão sendo cada vez mais pesquisados como um sistema inerentemente imprevisível, pois a incerteza de diferentes indivíduos se encontrando pela primeira vez torna a trajetória da equipe incognoscível.

Alguns dizem que a metáfora do caos—usada em teorias verbais—baseada em modelos matemáticos e aspectos psicológicos do comportamento humano fornece insights úteis para descrever a complexidade de pequenos grupos de trabalho, que vão além da própria metáfora.

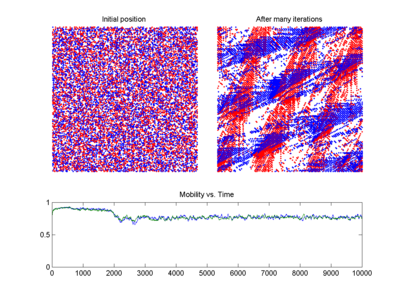
A previsão de tráfego pode se beneficiar das aplicações da teoria do caos. Melhores previsões de quando ocorrerá um congestionamento permitiriam que medidas fossem tomadas para dispersá-lo antes que ele ocorresse. A combinação dos princípios da teoria do caos com alguns outros métodos levou a um modelo de previsão de curto prazo mais preciso (veja o gráfico do modelo de tráfego BML à direita).

A teoria do caos foi aplicada aos dados ambientais do ciclo da água (também dados hidrológicos), como precipitação e vazão. Esses estudos produziram resultados controversos, porque os métodos para detectar uma assinatura caótica costumam ser relativamente subjetivos. Os primeiros estudos tendiam a "ter sucesso" em encontrar o caos, enquanto estudos subsequentes e meta-análises questionaram esses estudos e forneceram explicações sobre por que esses conjuntos de dados provavelmente não têm dinâmica caótica de baixa dimensão.

Na arte (predominantemente na teoria da arte), uma possível era pós-pós-moderna foi delineada com ênfase em narrativas múltiplas e na noção de que todo ângulo ficcional é uma possibilidade. Em parte, isso se deve a um discurso bissociado (trissociativo) e pode ser explicado com ênfase em um intercâmbio institucional de agentes subjetivistas.

Nota de direitos autorais

• Este artigo incorpora texto de um trabalho de conteúdo gratuito. Licenciado em CC-BY (declaração/permissão de licença). Texto retirado de três tipos de efeitos de borboleta dentro de modelos de Lorenz, Bo-Wen Shen, Roger A. Pielke, Sr., Xubin Zeng, Jialin Cui, Sara Faghih-Naini, Wei Paxson e Robert Atlas, MDPI. Enciclopédia. Para saber como adicionar texto de licença aberta aos artigos da Wikipédia, consulte esta página de como fazer. Para obter informações sobre a reutilização de texto da Wikipédia, consulte os termos de uso.