Teoria de controle

Teoria de controle é um campo da engenharia de controle e matemática aplicada que lida com o controle de sistemas dinâmicos em processos e máquinas de engenharia. O objetivo é desenvolver um modelo ou algoritmo que rege a aplicação de entradas do sistema para conduzir o sistema a um estado desejado, minimizando qualquer atraso, excesso ou estável -erro de estado e garantindo um nível de estabilidade de controle; muitas vezes com o objetivo de alcançar um grau de otimização.

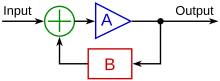
Para fazer isso, é necessário um controlador com o comportamento corretivo necessário. Este controlador monitora a variável de processo controlada (PV), e a compara com a referência ou ponto de ajuste (SP). A diferença entre o valor real e o valor desejado da variável de processo, chamada de sinal de erro, ou erro SP-PV, é aplicada como feedback para gerar uma ação de controle para trazer a variável de processo controlada para o mesmo valor que o ponto de ajuste. Outros aspectos também estudados são a controlabilidade e a observabilidade. A teoria de controle é usada na engenharia de sistemas de controle para projetar automação que revolucionou a fabricação, aeronaves, comunicações e outras indústrias e criou novos campos, como a robótica.

O uso extensivo geralmente é feito de um estilo esquemático conhecido como diagrama de blocos. Nele a função de transferência, também conhecida como função de sistema ou função de rede, é um modelo matemático da relação entre a entrada e a saída com base nas equações diferenciais que descrevem o sistema.

A teoria do controle data do século 19, quando a base teórica para a operação dos governadores foi descrita pela primeira vez por James Clerk Maxwell. A teoria do controle foi avançada por Edward Routh em 1874, Charles Sturm e em 1895, Adolf Hurwitz, que contribuíram para o estabelecimento de critérios de estabilidade de controle; e a partir de 1922, o desenvolvimento da teoria do controle PID por Nicolas Minorsky. Embora uma das principais aplicações da teoria de controle matemático seja na engenharia de sistemas de controle, que lida com o projeto de sistemas de controle de processo para a indústria, outras aplicações vão muito além disso. Como a teoria geral dos sistemas de feedback, a teoria do controle é útil sempre que o feedback ocorre - assim, a teoria do controle também tem aplicações em ciências da vida, engenharia da computação, sociologia e pesquisa operacional.

História

Governador centrífugo em um motor Boulton & Watt de 1788

Embora sistemas de controle de vários tipos remontem à antiguidade, uma análise mais formal do campo começou com uma análise dinâmica do governador centrífugo, realizada pelo físico James Clerk Maxwell em 1868, intitulada On Governors. Um regulador centrífugo já foi usado para regular a velocidade dos moinhos de vento. Maxwell descreveu e analisou o fenômeno da auto-oscilação, no qual atrasos no sistema podem levar a supercompensação e comportamento instável. Isso gerou uma onda de interesse no tópico, durante o qual o colega de classe de Maxwell, Edward John Routh, abstraiu os resultados de Maxwell para a classe geral de sistemas lineares. Independentemente, Adolf Hurwitz analisou a estabilidade do sistema usando equações diferenciais em 1877, resultando no que hoje é conhecido como teorema de Routh-Hurwitz.

Uma aplicação notável de controle dinâmico foi na área de voo tripulado. Os irmãos Wright fizeram seus primeiros voos de teste bem-sucedidos em 17 de dezembro de 1903 e se destacaram por sua capacidade de controlar seus voos por períodos substanciais (mais do que a capacidade de produzir sustentação de um aerofólio, que era conhecida). O controle contínuo e confiável do avião era necessário para voos com duração superior a alguns segundos.

Na Segunda Guerra Mundial, a teoria do controle estava se tornando uma importante área de pesquisa. Irmgard Flügge-Lotz desenvolveu a teoria dos sistemas de controle automático descontínuos e aplicou o princípio bang-bang ao desenvolvimento de equipamentos de controle automático de vôo para aeronaves. Outras áreas de aplicação para controles descontínuos incluem sistemas de controle de incêndio, sistemas de orientação e eletrônicos.

Às vezes, métodos mecânicos são usados para melhorar a estabilidade dos sistemas. Por exemplo, estabilizadores de navios são aletas montadas abaixo da linha d'água e emergindo lateralmente. Em embarcações contemporâneas, podem ser aletas ativas controladas por giroscópio, que têm a capacidade de mudar seu ângulo de ataque para neutralizar o rolamento causado pelo vento ou ondas que atuam no navio.

A Corrida Espacial também dependia do controle preciso de espaçonaves, e a teoria de controle também tem visto um uso crescente em campos como economia e inteligência artificial. Aqui, pode-se dizer que o objetivo é encontrar um modelo interno que obedeça ao teorema do bom regulador. Assim, por exemplo, em economia, quanto mais precisamente um modelo de negociação (ações ou commodities) representa as ações do mercado, mais facilmente ele pode controlar esse mercado (e extrair "trabalho útil" (lucros) de isto). Em IA, um exemplo pode ser um chatbot modelando o estado de discurso de humanos: quanto mais precisamente ele pode modelar o estado humano (por exemplo, em uma linha direta de suporte de voz por telefone), melhor ele pode manipular o humano (por exemplo, para executar as ações corretivas para resolver o problema que originou a chamada telefónica para a linha de apoio). Esses dois últimos exemplos pegam a estreita interpretação histórica da teoria de controle como um conjunto de equações diferenciais que modelam e regulam o movimento cinético e a ampliam em uma vasta generalização de um regulador interagindo com uma planta.

Controle de malha aberta e malha fechada (feedback)

Um temporizador eletromecânico, normalmente usado para controle de abertura baseado puramente em uma sequência de temporização, sem feedback do processo.

Fundamentalmente, existem dois tipos de loop de controle: controle de abertura (feedforward) e controle de loop fechado (feedback).

No controle open-loop, a ação de controle do controlador é independente da "produção de processo" (ou "variável de processo controlado"). Um bom exemplo disso é uma caldeira de aquecimento central controlada apenas por um temporizador, de modo que o calor é aplicado por um tempo constante, independentemente da temperatura do edifício. A ação de controle é o ligar/desligar da caldeira, mas a variável controlada deve ser a temperatura de construção, mas não é porque este é o controle de abertura da caldeira, que não dá controle de abertura da temperatura.

No controle de loop fechado, a ação de controle do controlador depende da saída do processo. No caso da analogia da caldeira, isso incluiria um termostato para monitorar a temperatura do edifício, e assim alimentar de volta um sinal para garantir que o controlador mantenha o edifício à temperatura definida no termostato. Um controlador de loop fechado, portanto, tem um loop de feedback que garante que o controlador exerce uma ação de controle para dar uma saída de processo da mesma que a "entrada de referência" ou "ponto definido". Por esta razão, controladores de loop fechados também são chamados controladores de feedback.

A definição de um sistema de controle de loop fechado de acordo com a British Standard Institution é "um sistema de controle que possui feedback de monitoramento, o sinal de desvio formado como resultado deste feedback que está sendo usado para controlar a ação de um elemento de controle final de modo a tender a reduzir o desvio para zero".

Da mesma forma: "A Sistema de controle de feedback é um sistema que tende a manter uma relação prescrita de uma variável de sistema para outra, comparando funções dessas variáveis e usando a diferença como meio de controle."

Teoria clássica de controle

Exemplo de um único circuito de controle industrial; mostrando controle modulado continuamente do fluxo de processo.

Um controlador de loop fechado ou controlador de feedback é um loop de controle que incorpora feedback, em contraste com um controlador open-loop ou controlador não-feedback. Um controlador de loop fechado usa feedback para controlar estados ou saídas de um sistema dinâmico. Seu nome vem do caminho da informação no sistema: entradas de processo (por exemplo, tensão aplicada a um motor elétrico) têm um efeito sobre as saídas do processo (por exemplo, velocidade ou torque do motor), que é medido com sensores e processado pelo controlador; o resultado (o sinal de controle) é "voltado" como entrada para o processo, fechando o loop.

No caso de sistemas de feedback linear, um loop de controle incluindo sensores, algoritmos de controle e atuadores é organizado em uma tentativa de regular uma variável em um setpoint (SP). Um exemplo diário é o controle de cruzeiro em um veículo de estrada; onde influências externas tais como colinas causaria mudanças de velocidade, e o motorista tem a capacidade de alterar a velocidade de jogo desejada. O algoritmo PID no controlador restaura a velocidade real para a velocidade desejada de uma forma ideal, com atraso mínimo ou overshoot, controlando a saída de energia do motor do veículo. Os sistemas de controle que incluem alguma detecção dos resultados que eles estão tentando alcançar estão fazendo uso de feedback e podem se adaptar a diferentes circunstâncias em certa medida. Os sistemas de controle de loop aberto não fazem uso de feedback e rodam apenas de maneiras pré-arranjadas.

Os controladores de loop fechado têm as seguintes vantagens sobre controladores de loop aberto:

• rejeição de distúrbios (como colinas no exemplo de controle de cruzeiro acima)
• desempenho garantido mesmo com incertezas modelo, quando a estrutura do modelo não corresponde perfeitamente ao processo real e os parâmetros do modelo não são exatos
• processos instáveis podem ser estabilizados
• sensibilidade reduzida às variações de parâmetros
• melhor desempenho de rastreamento de referência

Em alguns sistemas, o controle de abertura e loop fechado é usado simultaneamente. Em tais sistemas, o controle de abertura é denominado alimentação para e serve para melhorar ainda mais o desempenho de rastreamento de referência.

Uma arquitetura comum de controladores fechados é o controlador PID.

Um loop de feedback básico

Teoria de controle linear e não linear

O campo da teoria de controle pode ser dividido em dois ramos:

• Teoria do controle linear – Isso se aplica aos sistemas feitos de dispositivos que obedecem ao princípio de superposição, o que significa que a saída é proporcional à entrada. Eles são governados por equações diferenciais lineares. Uma subclasse principal é sistemas que além disso têm parâmetros que não mudam com o tempo, chamados tempo linear invariável (LTI) sistemas. Esses sistemas são amenáveis a técnicas matemáticas de domínio de frequência poderosas de grande generalidade, tais como a transformada de Laplace, a transformada de Fourier, a transformação de Z, a trama de Bode, o gafanhoto de raiz e o critério de estabilidade de Nyquist. Estes levam a uma descrição do sistema usando termos como largura de banda, resposta de frequência, eigenvalues, ganho, frequências ressonantes, zeros e pólos, que dão soluções para a resposta do sistema e técnicas de design para a maioria dos sistemas de interesse.
• Teoria do controle não linear – Isso abrange uma classe mais ampla de sistemas que não obedecem ao princípio da superposição, e se aplica a sistemas do mundo real porque todos os sistemas de controle reais não são lineares. Estes sistemas são frequentemente governados por equações diferenciais não lineares. As poucas técnicas matemáticas que foram desenvolvidas para lidar com elas são mais difíceis e muito menos gerais, muitas vezes aplicando-se apenas a categorias estreitas de sistemas. Estes incluem teoria do ciclo de limite, mapas de Poincaré, teorema da estabilidade de Lyapunov, e descrevendo funções. Os sistemas não lineares são frequentemente analisados usando métodos numéricos em computadores, por exemplo, simulando sua operação usando uma linguagem de simulação. Se apenas as soluções perto de um ponto estável são de interesse, os sistemas não lineares muitas vezes podem ser linearizados aproximando-os por um sistema linear usando a teoria da perturbação, e as técnicas lineares podem ser usadas.

Técnicas de análise - domínio da frequência e domínio do tempo

Técnicas matemáticas para analisar e projetar sistemas de controle se enquadram em duas categorias diferentes:

• Domínio de frequência – Neste tipo os valores das variáveis do estado, as variáveis matemáticas que representam a entrada, saída e feedback do sistema são representadas como funções de frequência. O sinal de entrada e a função de transferência do sistema são convertidos de funções de tempo para funções de frequência por uma transformação, como a transformada de Fourier, a transformada de Laplace ou a transformação de Z. A vantagem desta técnica é que resulta em uma simplificação da matemática; equações diferenciais que representam o sistema são substituídos por equações algébricas no domínio de frequência que é muito mais simples de resolver. No entanto, as técnicas de domínio de frequência só podem ser usadas com sistemas lineares, como mencionado acima.
• Representação do espaço do estado do domínio do tempo – Nesse tipo, os valores das variáveis do estado são representados como funções do tempo. Com este modelo, o sistema analisado é representado por uma ou mais equações diferenciais. Uma vez que as técnicas de domínio de frequência são limitadas a sistemas lineares, o domínio do tempo é amplamente utilizado para analisar sistemas não lineares do mundo real. Embora estes sejam mais difíceis de resolver, técnicas modernas de simulação de computador, como linguagens de simulação, fizeram sua rotina de análise.

Em contraste com a análise no domínio da frequência da teoria de controle clássica, a teoria de controle moderna utiliza a representação do espaço de estados no domínio do tempo, um modelo matemático de um sistema físico como um conjunto de variáveis de entrada, saída e estado relacionadas por variáveis de primeira ordem equações diferenciais. Para abstrair o número de entradas, saídas e estados, as variáveis são expressas como vetores e as equações diferenciais e algébricas são escritas em forma de matriz (esta última só é possível quando o sistema dinâmico é linear). A representação do espaço de estado (também conhecida como "abordagem no domínio do tempo") fornece uma maneira conveniente e compacta de modelar e analisar sistemas com várias entradas e saídas. Com entradas e saídas, de outra forma teríamos que escrever as transformadas de Laplace para codificar todas as informações sobre um sistema. Ao contrário da abordagem no domínio da frequência, o uso da representação em espaço de estados não se limita a sistemas com componentes lineares e condições iniciais nulas. "Espaço de estado" refere-se ao espaço cujos eixos são as variáveis de estado. O estado do sistema pode ser representado como um ponto dentro desse espaço.

Interface do sistema - SISO & MIMO

Os sistemas de controle podem ser divididos em diferentes categorias, dependendo do número de entradas e saídas.

• Entrada única (SISO) – Este é o tipo mais simples e mais comum, no qual uma saída é controlada por um sinal de controle. Exemplos são o exemplo de controle de cruzeiro acima, ou um sistema de áudio, no qual a entrada de controle é o sinal de áudio de entrada e a saída é as ondas sonoras do alto-falante.
• Multi-entrada de entrada (MIMO) – Estes são encontrados em sistemas mais complicados. Por exemplo, os grandes telescópios modernos, como o Keck e o MMT, possuem espelhos compostos por muitos segmentos separados, cada um controlado por um atuador. A forma de todo o espelho é constantemente ajustada por um sistema de controle de óptica ativa MIMO usando entrada de vários sensores no plano focal, para compensar mudanças na forma do espelho devido à expansão térmica, contração, tensões como é girado e distorção da frente de onda devido à turbulência na atmosfera. Sistemas complicados como reatores nucleares e células humanas são simulados por um computador como grandes sistemas de controle MIMO.

Projeto clássico do sistema SISO

O escopo da teoria clássica de controle é limitado ao projeto de sistema de entrada única e saída única (SISO), exceto ao analisar a rejeição de distúrbios usando uma segunda entrada. A análise do sistema é realizada no domínio do tempo por meio de equações diferenciais, no domínio dos complexos com a transformada de Laplace ou no domínio da frequência pela transformação do domínio dos complexos. Muitos sistemas podem ser assumidos como tendo uma resposta de sistema de segunda ordem e variável única no domínio do tempo. Um controlador projetado usando a teoria clássica geralmente requer ajuste no local devido a aproximações de projeto incorretas. No entanto, devido à implementação física mais fácil de projetos de controladores clássicos em comparação com sistemas projetados usando teoria de controle moderna, esses controladores são preferidos na maioria das aplicações industriais. Os controladores mais comuns projetados usando a teoria clássica de controle são os controladores PID. Uma implementação menos comum pode incluir um ou ambos os filtros Lead ou Lag. O objetivo final final é atender aos requisitos normalmente fornecidos no domínio do tempo chamado resposta ao degrau ou, às vezes, no domínio da frequência, chamado resposta em malha aberta. As características de resposta ao degrau aplicadas em uma especificação são tipicamente ultrapassagem percentual, tempo de acomodação, etc. As características de resposta de malha aberta aplicadas em uma especificação são tipicamente margem de ganho e fase e largura de banda. Estas características podem ser avaliadas através de simulação incluindo um modelo dinâmico do sistema sob controle acoplado ao modelo de compensação.

Design de sistema MIMO moderno

A teoria de controle moderna é realizada no espaço de estados e pode lidar com sistemas de múltiplas entradas e múltiplas saídas (MIMO). Isso supera as limitações da teoria de controle clássica em problemas de projeto mais sofisticados, como o controle de aeronaves de caça, com a limitação de que nenhuma análise no domínio da frequência é possível. No projeto moderno, um sistema é representado com a maior vantagem como um conjunto de equações diferenciais de primeira ordem desacopladas definidas usando variáveis de estado. As teorias de controle não linear, multivariável, adaptativo e robusto entram nesta divisão. Métodos matriciais são significativamente limitados para sistemas MIMO onde a independência linear não pode ser assegurada na relação entre entradas e saídas. Sendo relativamente nova, a teoria de controle moderna tem muitas áreas ainda a serem exploradas. Estudiosos como Rudolf E. Kálmán e Aleksandr Lyapunov são bem conhecidos entre as pessoas que moldaram a moderna teoria de controle.

Tópicos em teoria de controle

Estabilidade

A estabilidade de um sistema dinâmico geral sem entrada pode ser descrita com os critérios de estabilidade de Lyapunov.

• Um sistema linear é chamado de de entrada limitada (BIBO) estável se sua saída permanecer limitada para qualquer entrada limitada.
• A estabilidade para sistemas não lineares que tomam uma entrada é a estabilidade de entrada para estado (ISS), que combina a estabilidade de Lyapunov e uma noção semelhante à estabilidade da BIBO.

Para simplificar, as descrições a seguir se concentram em sistemas lineares de tempo contínuo e tempo discreto.

Matematicamente, isso significa que, para um sistema linear causal ser estável, todos os pólos de sua função de transferência devem ter valores reais negativos, ou seja, a parte real de cada pólo deve ser menor que zero. Na prática, a estabilidade requer que os polos complexos da função de transferência residam

• na metade esquerda aberta do plano complexo para o tempo contínuo, quando a transformada Laplace é usada para obter a função de transferência.
• dentro do círculo da unidade para tempo discreto, quando o Z-transform é usado.

A diferença entre os dois casos é simplesmente devido ao método tradicional de plotagem de tempo contínuo versus funções de transferência de tempo discretas. O contínuo Laplace transforma-se em coordenadas cartesianas onde o $Não.$ eixo é o eixo real e o Z-transform discreto está em coordenadas circulares onde o $- Sim.$ eixo é o eixo real.

Quando as condições apropriadas acima são satisfeitas, um sistema é dito assintoticamente estável; as variáveis de um sistema de controle assintoticamente estável sempre diminuem de seu valor inicial e não apresentam oscilações permanentes. As oscilações permanentes ocorrem quando um pólo tem uma parte real exatamente igual a zero (no caso de tempo contínuo) ou um módulo igual a um (no caso de tempo discreto). Se uma resposta de sistema simplesmente estável não decai nem cresce com o tempo e não apresenta oscilações, ela é marginalmente estável; neste caso, a função de transferência do sistema possui pólos não repetidos na origem do plano complexo (ou seja, seu componente real e complexo é zero no caso de tempo contínuo). As oscilações estão presentes quando os pólos com parte real igual a zero têm uma parte imaginária diferente de zero.

Se um sistema em questão tiver uma resposta ao impulso de

${displaystyle x[n]=0.5^{n}u[n]}$

então a transformada Z (veja este exemplo), é dada por

${displaystyle X(z)={frac {1}{1-0.5z^{-1}}$

que tem um pólo em $- Sim.$ (parte zero imaginária). Este sistema é BIBO (assintoticamente) estável desde que o pólo é interior o círculo da unidade.

No entanto, se a resposta ao impulso foi

${displaystyle x[n]=1.5^{n}u[n]}$

então a transformada Z é

${displaystyle X(z)={frac {1}{1-1.5z^{-1}}$

que tem um pólo em $- Sim.$ e não é BIBO estável desde que o pólo tem um módulo estritamente maior do que um.

Existem inúmeras ferramentas para a análise dos pólos de um sistema. Estes incluem sistemas gráficos como o lugar das raízes, gráficos de Bode ou gráficos de Nyquist.

Mudanças mecânicas podem tornar os equipamentos (e sistemas de controle) mais estáveis. Os marinheiros adicionam lastro para melhorar a estabilidade dos navios. Os navios de cruzeiro usam aletas antirrolagem que se estendem transversalmente da lateral do navio por cerca de 30 pés (10 m) e giram continuamente em torno de seus eixos para desenvolver forças que se opõem à rolagem.

Controlabilidade e observabilidade

Controlabilidade e observabilidade são questões fundamentais na análise de um sistema antes de decidir a melhor estratégia de controle a ser aplicada, ou mesmo se é possível controlar ou estabilizar o sistema. A controlabilidade está relacionada à possibilidade de forçar o sistema a um determinado estado usando um sinal de controle apropriado. Se um estado não for controlável, nenhum sinal será capaz de controlar o estado. Se um estado não é controlável, mas sua dinâmica é estável, então o estado é denominado estabilizável. A observabilidade, ao contrário, está relacionada à possibilidade de observar, por meio de medições de saída, o estado de um sistema. Se um estado não for observável, o controlador nunca será capaz de determinar o comportamento de um estado não observável e, portanto, não poderá usá-lo para estabilizar o sistema. No entanto, semelhante à condição de estabilização acima, se um estado não puder ser observado, ele ainda poderá ser detectado.

Do ponto de vista geométrico, observando os estados de cada variável do sistema a ser controlado, cada "ruim" O estado dessas variáveis deve ser controlável e observável para garantir um bom comportamento no sistema em malha fechada. Ou seja, se um dos autovalores do sistema não for controlável e observável, essa parte da dinâmica permanecerá intocada no sistema de malha fechada. Se tal autovalor não for estável, a dinâmica desse autovalor estará presente no sistema em malha fechada que, portanto, será instável. Pólos inobserváveis não estão presentes na realização da função de transferência de uma representação no espaço de estado, razão pela qual às vezes a última é preferida na análise de sistemas dinâmicos.

Soluções para problemas de um sistema incontrolável ou inobservável incluem a adição de atuadores e sensores.

Especificação de controle

Várias estratégias de controle diferentes foram desenvolvidas nos últimos anos. Estes variam desde os extremamente gerais (controlador PID), até outros dedicados a classes muito particulares de sistemas (especialmente robótica ou controle de cruzeiro de aeronaves).

Um problema de controle pode ter várias especificações. A estabilidade, é claro, está sempre presente. O controlador deve garantir que o sistema de loop fechado é estável, independentemente da estabilidade de abertura. Uma escolha pobre do controlador pode até piorar a estabilidade do sistema de abertura, que deve ser evitado normalmente. Às vezes seria desejado obter dinâmica particular no loop fechado: ou seja, que os pólos têm $Não. Re[lambda])$, onde ${displaystyle {overline})$ é um valor fixo estritamente maior do que zero, em vez de simplesmente pedir que $Não. Re[lambda]$.

Outra especificação típica é a rejeição de um distúrbio de degrau; incluir um integrador na cadeia de malha aberta (ou seja, diretamente antes do sistema sob controle) consegue isso facilmente. Outras classes de distúrbios precisam de diferentes tipos de subsistemas para serem incluídos.

Outros "clássicos" as especificações da teoria de controle consideram a resposta temporal do sistema em malha fechada. Estes incluem o tempo de subida (o tempo necessário para o sistema de controle atingir o valor desejado após uma perturbação), overshoot de pico (o maior valor alcançado pela resposta antes de atingir o valor desejado) e outros (tempo de estabilização, quarto de decaimento). As especificações do domínio de frequência geralmente estão relacionadas à robustez (veja a seguir).

Avaliações de desempenho modernas usam alguma variação de erro de rastreamento integrado (IAE, ISA, CQI).

Identificação e robustez do modelo

Um sistema de controle deve sempre ter alguma propriedade de robustez. Um controlador robusto é tal que suas propriedades não mudam muito se aplicado a um sistema ligeiramente diferente do matemático utilizado para sua síntese. Este requisito é importante, pois nenhum sistema físico real realmente se comporta como a série de equações diferenciais usadas para representá-lo matematicamente. Normalmente, um modelo matemático mais simples é escolhido para simplificar os cálculos, caso contrário, a verdadeira dinâmica do sistema pode ser tão complicada que um modelo completo é impossível.

Identificação do sistema

O processo de determinação das equações que regem a dinâmica do modelo é chamado de identificação do sistema. Isso pode ser feito off-line: por exemplo, executando uma série de medidas a partir das quais para calcular um modelo matemático aproximado, tipicamente sua função de transferência ou matriz. Tal identificação da saída, no entanto, não pode ter em conta a dinâmica não-observável. Às vezes, o modelo é construído diretamente a partir de equações físicas conhecidas, por exemplo, no caso de um sistema de massa-prima-dano sabemos que ${displaystyle m{ddot {x}}(t)=-Kx(t)-mathrm {B} {dot {x}}(t)}$. Mesmo assumindo que um modelo "completo" é usado na concepção do controlador, todos os parâmetros incluídos nessas equações (chamadas de "parâmetros nominais") nunca são conhecidos com precisão absoluta; o sistema de controle terá que se comportar corretamente mesmo quando conectado a um sistema físico com valores de parâmetro verdadeiros longe do nominal.

Algumas técnicas avançadas de controle incluem um controle "on-line" processo de identificação (ver adiante). Os parâmetros do modelo são calculados ("identificados") enquanto o próprio controlador está em execução. Desta forma, se ocorrer uma variação drástica dos parâmetros, por exemplo, se o braço do robô soltar um peso, o controlador se ajustará consequentemente para garantir o desempenho correto.

Análise

A análise da robustez de um sistema de controle SISO (single input single output) pode ser realizada no domínio da frequência, considerando a função de transferência do sistema e usando diagramas de Nyquist e Bode. Os tópicos incluem ganho e margem de fase e margem de amplitude. Para MIMO (multi-input multi-output) e, em geral, sistemas de controle mais complicados, deve-se considerar os resultados teóricos concebidos para cada técnica de controle (ver a próxima seção). Ou seja, se forem necessárias qualidades específicas de robustez, o engenheiro deve desviar sua atenção para uma técnica de controle, incluindo essas qualidades em suas propriedades.

Restrições

Um problema específico de robustez é o requisito para um sistema de controle funcionar adequadamente na presença de restrições de entrada e estado. No mundo físico todo sinal é limitado. Pode acontecer que um controlador envie sinais de controle que não podem ser seguidos pelo sistema físico, por exemplo, tentando girar uma válvula em velocidade excessiva. Isso pode produzir comportamento indesejado do sistema de malha fechada ou até mesmo danificar ou quebrar atuadores ou outros subsistemas. Técnicas de controle específicas estão disponíveis para resolver o problema: controle preditivo de modelo (veja mais adiante) e sistemas anti-wind up. Este último consiste em um bloco de controle adicional que garante que o sinal de controle nunca exceda um determinado limite.

Classificações do sistema

Controle de sistemas lineares

Para sistemas MIMO, a colocação de polos pode ser realizada matematicamente usando uma representação de espaço de estado do sistema de malha aberta e calculando uma matriz de realimentação atribuindo polos nas posições desejadas. Em sistemas complicados, isso pode exigir recursos de cálculo assistidos por computador e nem sempre garante robustez. Além disso, todos os estados do sistema não são geralmente medidos e, portanto, os observadores devem ser incluídos e incorporados no projeto de posicionamento do pólo.

Controle de sistemas não lineares

Processos em indústrias como a robótica e a indústria aeroespacial geralmente têm forte dinâmica não linear. Na teoria de controle às vezes é possível linearizar tais classes de sistemas e aplicar técnicas lineares, mas em muitos casos pode ser necessário elaborar teorias do zero que permitam o controle de sistemas não lineares. Estes, por exemplo, linearização de feedback, retrocesso, controle de modo deslizante, controle de linearização de trajetória normalmente tiram vantagem dos resultados baseados na teoria de Lyapunov. A geometria diferencial tem sido amplamente utilizada como uma ferramenta para generalizar conceitos de controle linear bem conhecidos para o caso não linear, bem como mostrar as sutilezas que o tornam um problema mais desafiador. A teoria do controle também foi usada para decifrar o mecanismo neural que dirige os estados cognitivos.

Controle de sistemas descentralizados

Quando o sistema é controlado por vários controladores, o problema é de controle descentralizado. A descentralização é útil de várias maneiras, por exemplo, ajuda os sistemas de controle a operar em uma área geográfica maior. Os agentes em sistemas de controle descentralizados podem interagir por meio de canais de comunicação e coordenar suas ações.

Controle de sistemas determinístico e estocástico

Um problema de controle estocástico é aquele em que a evolução das variáveis de estado está sujeita a choques aleatórios de fora do sistema. Um problema de controle determinístico não está sujeito a choques aleatórios externos.

Principais estratégias de controle

Todo sistema de controle deve garantir primeiro a estabilidade do comportamento de malha fechada. Para sistemas lineares, isso pode ser obtido colocando os pólos diretamente. Os sistemas de controle não linear usam teorias específicas (normalmente baseadas na teoria de Aleksandr Lyapunov) para garantir a estabilidade sem levar em consideração a dinâmica interna do sistema. A possibilidade de atender diferentes especificações varia do modelo considerado e da estratégia de controle escolhida.

Lista das principais técnicas de controle

• O controle adaptativo usa a identificação on-line dos parâmetros do processo, ou a modificação dos ganhos do controlador, obtendo assim propriedades robustas fortes. Os controles adaptativos foram aplicados pela primeira vez na indústria aeroespacial na década de 1950, e encontraram um sucesso particular nesse campo.
• Um sistema de controle hierárquico é um tipo de sistema de controle em que um conjunto de dispositivos e software de governo é organizado em uma árvore hierárquica. Quando as ligações na árvore são implementadas por uma rede de computadores, então esse sistema de controle hierárquico também é uma forma de sistema de controle em rede.
• O controle inteligente usa várias abordagens de computação AI como redes neurais artificiais, probabilidade bayesiana, lógica fuzzy, aprendizado de máquina, computação evolutiva e algoritmos genéticos ou uma combinação desses métodos, como algoritmos neuro-fuzzy, para controlar um sistema dinâmico.
• O controle ideal é uma técnica de controle particular na qual o sinal de controle otimiza um certo "índice de custo": por exemplo, no caso de um satélite, os impulsos de jato necessários para trazê-lo à trajetória desejada que consomem a menor quantidade de combustível. Dois métodos ideais de design de controle foram amplamente utilizados em aplicações industriais, uma vez que tem sido mostrado que podem garantir a estabilidade de loop fechado. Estes são Model Predictive Control (MPC) e controle linear-quadratic-Gaussian (LQG). O primeiro pode mais explicitamente levar em conta restrições sobre os sinais no sistema, que é uma característica importante em muitos processos industriais. No entanto, a estrutura "controle otimizado" no MPC é apenas um meio para alcançar tal resultado, pois não otimiza um verdadeiro índice de desempenho do sistema de controle de loop fechado. Juntamente com controladores PID, os sistemas MPC são a técnica de controle mais utilizada no controle de processo.
• O controle robusto lida explicitamente com a incerteza em sua abordagem ao design do controlador. Controladores projetados usando controle robusto métodos tendem a ser capazes de lidar com pequenas diferenças entre o verdadeiro sistema e o modelo nominal usado para o design. Os primeiros métodos de Bode e outros foram bastante robustos; os métodos do espaço-espaço do estado inventados na década de 1960 e 1970 às vezes foram encontrados para falta de robustez. Exemplos de modernas técnicas de controle robustas incluem H-infinity loop-shaping desenvolvido por Duncan McFarlane e Keith Glover, controle de modo de deslizamento (SMC) desenvolvido pela Vadim Utkin, e protocolos seguros projetados para controle de grandes populações heterogêneas de cargas elétricas em aplicações Smart Power Grid. Os métodos robustos visam alcançar um desempenho robusto e/ou estabilidade na presença de pequenos erros de modelagem.
• Controle estocástico lida com o projeto de controle com incerteza no modelo. Em problemas de controle estocástico típicos, presume-se que existem ruídos aleatórios e distúrbios no modelo e no controlador, e o projeto de controle deve levar em conta esses desvios aleatórios.
• O controle de criticidade auto-organizado pode ser definido como tentativas de interferir nos processos pelos quais o sistema auto-organizado dissipa a energia.

Pessoas em sistemas e controle

Muitas figuras ativas e históricas fizeram contribuições significativas para a teoria de controle, incluindo

• Pierre-Simon Laplace inventou o Z-transform em seu trabalho sobre teoria da probabilidade, agora usado para resolver problemas da teoria do controle do tempo discreto. O Z-transform é um equivalente de tempo discreto da transformada Laplace que é nomeada após ele.
• Irmgard Flugge-Lotz desenvolveu a teoria do controle automático descontinuado e aplicou-o aos sistemas de controle automático de aeronaves.
• Alexander Lyapunov na década de 1890 marca o início da teoria da estabilidade.
• Harold S. Black inventou o conceito de amplificadores de feedback negativo em 1927. Ele conseguiu desenvolver amplificadores de feedback negativo estáveis na década de 1930.
• Harry Nyquist desenvolveu o critério de estabilidade Nyquist para sistemas de feedback na década de 1930.
• Richard Bellman desenvolveu programação dinâmica na década de 1940.
• Warren E. Dixon, o teórico do controle e um professor
• Andrey Kolmogorov co-desenvolveu o filtro Wiener–Kolmogorov em 1941.
• Norbert Wiener co-desenvolveu o filtro Wiener-Kolmogorov e cunhou o termo cibernética na década de 1940.
• John R. Ragazzini introduziu o controle digital e o uso da teoria de controle Z-transform (inventado por Laplace) na década de 1950.
• Lev Pontryagin introduziu o princípio máximo e o princípio bang-bang.
• Pierre-Louis Lions desenvolveu soluções de viscosidade em controle estocástico e métodos de controle ideais.
• Rudolf E. Kálmán foi pioneiro na abordagem do estado-espaço para sistemas e controle. Introduziu as noções de controlabilidade e observabilidade. Desenvolveu o filtro Kalman para estimativa linear.
• Ali H. Nayfeh, que foi um dos principais contribuidores da teoria de controle não linear e publicou muitos livros sobre métodos de perturbação
• Jan C. Willems Introduziu o conceito de dissipatividade, como uma generalização da função Lyapunov para sistemas de entrada/estado/saída. A construção da função de armazenamento, como o análogo de uma função de Lyapunov é chamada, levou ao estudo da desigualdade de matriz linear (LMI) na teoria de controle. Ele foi pioneiro na abordagem comportamental da teoria dos sistemas matemáticos.