Teoria das cordas

Na física, a teoria das cordas é uma estrutura teórica na qual as partículas pontuais da física de partículas são substituídas por objetos unidimensionais chamados cordas. A teoria das cordas descreve como essas cordas se propagam pelo espaço e interagem entre si. Em escalas de distância maiores que a escala das cordas, uma corda se parece exatamente com uma partícula comum, com sua massa, carga e outras propriedades determinadas pelo estado vibracional da corda. Na teoria das cordas, um dos muitos estados vibracionais da corda corresponde ao gráviton, uma partícula da mecânica quântica que carrega a força gravitacional. Assim, a teoria das cordas é uma teoria da gravidade quântica.

A teoria das cordas é um assunto amplo e variado que tenta abordar uma série de questões profundas da física fundamental. A teoria das cordas contribuiu com uma série de avanços para a física matemática, que foram aplicados a uma variedade de problemas na física dos buracos negros, na cosmologia do universo primitivo, na física nuclear e na física da matéria condensada, e estimulou uma série de desenvolvimentos importantes na matemática pura.. Como a teoria das cordas fornece potencialmente uma descrição unificada da gravidade e da física das partículas, ela é candidata a uma teoria de tudo, um modelo matemático independente que descreve todas as forças e formas fundamentais da matéria. Apesar de muito trabalho sobre estes problemas, não se sabe até que ponto a teoria das cordas descreve o mundo real ou quanta liberdade a teoria permite na escolha dos seus detalhes.

A teoria das cordas foi estudada pela primeira vez no final da década de 1960 como uma teoria da força nuclear forte, antes de ser abandonada em favor da cromodinâmica quântica. Posteriormente, percebeu-se que as próprias propriedades que tornavam a teoria das cordas inadequada como teoria da física nuclear a tornavam uma candidata promissora para uma teoria quântica da gravidade. A versão mais antiga da teoria das cordas, a teoria bosônica das cordas, incorporou apenas a classe de partículas conhecidas como bósons. Mais tarde, desenvolveu-se a teoria das supercordas, que postula uma conexão chamada supersimetria entre os bósons e a classe de partículas chamadas férmions. Cinco versões consistentes da teoria das supercordas foram desenvolvidas antes de se conjecturar, em meados da década de 1990, que eram todos casos limites diferentes de uma única teoria em 11 dimensões, conhecida como teoria M. No final de 1997, os teóricos descobriram uma relação importante chamada correspondência anti-de Sitter/teoria de campo conforme (correspondência AdS/CFT), que relaciona a teoria das cordas a outro tipo de teoria física chamada teoria quântica de campos.

Um dos desafios da teoria das cordas é que a teoria completa não tem uma definição satisfatória em todas as circunstâncias. Outra questão é que se pensa que a teoria descreve uma enorme paisagem de universos possíveis, o que complicou os esforços para desenvolver teorias da física de partículas baseadas na teoria das cordas. Estas questões levaram alguns membros da comunidade a criticar estas abordagens da física e a questionar o valor da investigação contínua sobre a unificação da teoria das cordas.

Fundamentos

Visão geral

No século 20, surgiram duas estruturas teóricas para a formulação das leis da física. A primeira é a teoria geral da relatividade de Albert Einstein, uma teoria que explica a força da gravidade e a estrutura do espaço-tempo no nível macro. A outra é a mecânica quântica, uma formulação completamente diferente, que utiliza princípios de probabilidade conhecidos para descrever fenômenos físicos no nível micro. No final da década de 1970, essas duas estruturas provaram ser suficientes para explicar a maioria das características observadas no universo, desde partículas elementares até átomos, até a evolução das estrelas e do universo como um todo.

Apesar destes sucessos, ainda existem muitos problemas que precisam ser resolvidos. Um dos problemas mais profundos da física moderna é o problema da gravidade quântica. A teoria geral da relatividade é formulada no âmbito da física clássica, enquanto as outras forças fundamentais são descritas no âmbito da mecânica quântica. Uma teoria quântica da gravidade é necessária para conciliar a relatividade geral com os princípios da mecânica quântica, mas surgem dificuldades quando se tenta aplicar as prescrições usuais da teoria quântica à força da gravidade. Além do problema de desenvolver uma teoria consistente da gravidade quântica, existem muitos outros problemas fundamentais na física dos núcleos atômicos, dos buracos negros e do universo primitivo.

A teoria das cordas é uma estrutura teórica que tenta abordar essas questões e muitas outras. O ponto de partida para a teoria das cordas é a ideia de que as partículas pontuais da física de partículas também podem ser modeladas como objetos unidimensionais chamados cordas. A teoria das cordas descreve como as cordas se propagam pelo espaço e interagem umas com as outras. Numa determinada versão da teoria das cordas, existe apenas um tipo de corda, que pode parecer um pequeno laço ou segmento de corda comum, e pode vibrar de diferentes maneiras. Em escalas de distância maiores que a escala das cordas, uma corda parecerá uma partícula comum, com sua massa, carga e outras propriedades determinadas pelo estado vibracional da corda. Desta forma, todas as diferentes partículas elementares podem ser vistas como cordas vibrantes. Na teoria das cordas, um dos estados vibracionais da corda dá origem ao gráviton, uma partícula da mecânica quântica que carrega força gravitacional. Assim, a teoria das cordas é uma teoria da gravidade quântica.

Um dos principais desenvolvimentos das últimas décadas na teoria das cordas foi a descoberta de certas “dualidades”, transformações matemáticas que identificam uma teoria física com outra. Os físicos que estudam a teoria das cordas descobriram uma série dessas dualidades entre as diferentes versões da teoria das cordas, e isso levou à conjectura de que todas as versões consistentes da teoria das cordas estão agrupadas em uma única estrutura conhecida como teoria M.

Os estudos da teoria das cordas também produziram vários resultados sobre a natureza dos buracos negros e a interação gravitacional. Existem certos paradoxos que surgem quando se tenta compreender os aspectos quânticos dos buracos negros, e o trabalho na teoria das cordas tem tentado esclarecer estas questões. No final de 1997, esta linha de trabalho culminou na descoberta da correspondência anti-de Sitter/teoria de campo conforme ou AdS/CFT. Este é um resultado teórico que relaciona a teoria das cordas com outras teorias físicas que são melhor compreendidas teoricamente. A correspondência AdS/CFT tem implicações para o estudo de buracos negros e da gravidade quântica, e tem sido aplicada a outros assuntos, incluindo física nuclear e da matéria condensada.

Como a teoria das cordas incorpora todas as interações fundamentais, incluindo a gravidade, muitos físicos esperam que ela acabe sendo desenvolvida ao ponto de descrever completamente o nosso universo, tornando-a uma teoria de tudo. Um dos objetivos das pesquisas atuais em teoria das cordas é encontrar uma solução da teoria que reproduza o espectro observado de partículas elementares, com uma pequena constante cosmológica, contendo matéria escura e um mecanismo plausível de inflação cósmica. Embora tenha havido progresso em direção a esses objetivos, não se sabe até que ponto a teoria das cordas descreve o mundo real ou quanta liberdade a teoria permite na escolha dos detalhes.

Um dos desafios da teoria das cordas é que a teoria completa não tem uma definição satisfatória em todas as circunstâncias. O espalhamento de cordas é definido de forma mais direta usando as técnicas da teoria das perturbações, mas em geral não se sabe como definir a teoria das cordas de forma não perturbativa. Também não está claro se existe algum princípio pelo qual a teoria das cordas seleciona o seu estado de vácuo, o estado físico que determina as propriedades do nosso universo. Estes problemas levaram alguns membros da comunidade a criticar estas abordagens à unificação da física e a questionar o valor da investigação contínua sobre estes problemas.

Sequências

A aplicação da mecânica quântica a objetos físicos como o campo eletromagnético, que se estendem no espaço e no tempo, é conhecida como teoria quântica de campos. Na física de partículas, as teorias quânticas de campos formam a base para a nossa compreensão das partículas elementares, que são modeladas como excitações nos campos fundamentais.

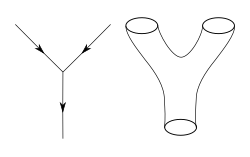
Na teoria quântica de campos, normalmente calculam-se as probabilidades de vários eventos físicos usando as técnicas da teoria das perturbações. Desenvolvida por Richard Feynman e outros na primeira metade do século XX, a teoria quântica de campos perturbativos usa diagramas especiais chamados diagramas de Feynman para organizar os cálculos. Imagina-se que esses diagramas representam os caminhos das partículas pontuais e suas interações.

O ponto de partida para a teoria das cordas é a ideia de que as partículas pontuais da teoria quântica de campos também podem ser modeladas como objetos unidimensionais chamados cordas. A interação das cordas é definida de maneira mais direta pela generalização da teoria de perturbação usada na teoria quântica de campos comum. No nível dos diagramas de Feynman, isso significa substituir o diagrama unidimensional que representa o caminho de uma partícula pontual por uma superfície bidimensional (2D) que representa o movimento de uma corda. Ao contrário da teoria quântica de campos, a teoria das cordas não tem uma definição completa não perturbativa, pelo que muitas das questões teóricas que os físicos gostariam de responder permanecem fora de alcance.

Nas teorias da física de partículas baseadas na teoria das cordas, presume-se que a escala de comprimento característico das cordas seja da ordem do comprimento de Planck, ou 10⁻³⁵ metros, a escala na qual se acredita que os efeitos da gravidade quântica se tornem significativos. Em escalas de comprimento muito maiores, como as escalas visíveis nos laboratórios de física, tais objetos seriam indistinguíveis de partículas pontuais de dimensão zero, e o estado vibracional da corda determinaria o tipo de partícula. Um dos estados vibracionais de uma corda corresponde ao gráviton, uma partícula da mecânica quântica que carrega a força gravitacional.

A versão original da teoria das cordas era a teoria bosônica das cordas, mas esta versão descrevia apenas bósons, uma classe de partículas que transmitem forças entre as partículas de matéria, ou férmions. A teoria das cordas bosônicas acabou sendo substituída por teorias chamadas teorias das supercordas. Essas teorias descrevem bósons e férmions e incorporam uma ideia teórica chamada supersimetria. Nas teorias com supersimetria, cada bóson tem uma contraparte que é um férmion e vice-versa.

Existem diversas versões da teoria das supercordas: tipo I, tipo IIA, tipo IIB e dois tipos de teoria das cordas heteróticas (SO(32) e E8×E8). As diferentes teorias permitem diferentes tipos de cordas, e as partículas que surgem em baixas energias exibem simetrias diferentes. Por exemplo, a teoria do tipo I inclui cordas abertas (que são segmentos com extremidades) e cordas fechadas (que formam loops fechados), enquanto os tipos IIA, IIB e heteróticos incluem apenas cordas fechadas.

Dimensões extras

Na vida cotidiana, existem três dimensões familiares (3D) de espaço: altura, largura e comprimento. A teoria geral da relatividade de Einstein trata o tempo como uma dimensão equivalente às três dimensões espaciais; na relatividade geral, o espaço e o tempo não são modelados como entidades separadas, mas sim unificados em um espaço-tempo quadridimensional (4D). Neste quadro, o fenómeno da gravidade é visto como uma consequência da geometria do espaço-tempo.

Apesar de o Universo ser bem descrito pelo espaço-tempo 4D, existem várias razões pelas quais os físicos consideram teorias em outras dimensões. Em alguns casos, ao modelar o espaço-tempo num número diferente de dimensões, uma teoria torna-se mais tratável matematicamente e pode-se realizar cálculos e obter conhecimentos gerais com mais facilidade. Existem também situações em que teorias em duas ou três dimensões do espaço-tempo são úteis para descrever fenômenos na física da matéria condensada. Finalmente, existem cenários em que poderia realmente haver mais de 4D de espaço-tempo que, no entanto, conseguiram escapar à detecção.

As teorias das cordas requerem dimensões extras do espaço-tempo para sua consistência matemática. Na teoria das cordas bosônicas, o espaço-tempo tem 26 dimensões, enquanto na teoria das supercordas é 10 dimensões e na teoria M é 11 dimensões. Para descrever fenómenos físicos reais utilizando a teoria das cordas, deve-se, portanto, imaginar cenários em que estas dimensões extras não seriam observadas em experiências.

A compactação é uma forma de modificar o número de dimensões em uma teoria física. Na compactação, assume-se que algumas das dimensões extras estão "fechadas" sobre si mesmos para formar círculos. No limite onde estas dimensões enroladas se tornam muito pequenas, obtém-se uma teoria em que o espaço-tempo tem efectivamente um número menor de dimensões. Uma analogia padrão para isso é considerar um objeto multidimensional, como uma mangueira de jardim. Se a mangueira for vista de uma distância suficiente, ela parece ter apenas uma dimensão, o seu comprimento. Porém, ao nos aproximarmos da mangueira, descobrimos que ela contém uma segunda dimensão, a sua circunferência. Assim, uma formiga rastejando na superfície da mangueira se moveria em duas dimensões.

A compactação pode ser usada para construir modelos nos quais o espaço-tempo é efetivamente quadridimensional. No entanto, nem todas as formas de compactar as dimensões extras produzem um modelo com as propriedades certas para descrever a natureza. Em um modelo viável de física de partículas, as dimensões extras compactas devem ter a forma de uma variedade Calabi-Yau. Uma variedade Calabi-Yau é um espaço especial que normalmente é considerado hexadimensional em aplicações à teoria das cordas. Seu nome é uma homenagem aos matemáticos Eugenio Calabi e Shing-Tung Yau.

Outra abordagem para reduzir o número de dimensões é o chamado cenário mundial de brana. Nesta abordagem, os físicos assumem que o universo observável é um subespaço quadridimensional de um espaço de dimensão superior. Nesses modelos, os bósons portadores de força da física de partículas surgem de cordas abertas com extremidades ligadas ao subespaço quadridimensional, enquanto a gravidade surge de cordas fechadas que se propagam através do espaço ambiente maior. Esta ideia desempenha um papel importante nas tentativas de desenvolver modelos de física do mundo real baseados na teoria das cordas e fornece uma explicação natural para a fraqueza da gravidade em comparação com outras forças fundamentais.

Dualidades

Um fato notável sobre a teoria das cordas é que todas as diferentes versões da teoria estão relacionadas de maneiras altamente não triviais. Uma das relações que podem existir entre diferentes teorias de cordas é chamada de S-dualidade. Esta é uma relação que diz que uma coleção de partículas que interagem fortemente numa teoria pode, em alguns casos, ser vista como uma coleção de partículas que interagem fracamente numa teoria completamente diferente. Grosso modo, diz-se que um conjunto de partículas interage fortemente se se combinam e decaem com frequência e interage fracamente se o fazem com pouca frequência. A teoria das cordas do tipo I acaba sendo equivalente pela dualidade S à SO(32) teoria das cordas heteróticas. Da mesma forma, a teoria das cordas do tipo IIB está relacionada a si mesma de uma forma não trivial pela S-dualidade.

Outra relação entre diferentes teorias de cordas é a dualidade-T. Aqui consideramos strings se propagando em torno de uma dimensão extra circular. A dualidade T afirma que uma string se propagando em torno de um círculo de raio R é equivalente a uma string se propagando em torno de um círculo de raio 1/R no sentido de que todas as quantidades observáveis em uma descrição são identificadas com quantidades na descrição dupla. Por exemplo, uma corda tem impulso à medida que se propaga em torno de um círculo e também pode enrolar-se em torno do círculo uma ou mais vezes. O número de vezes que a corda gira em torno de um círculo é chamado de número do enrolamento. Se uma string tem impulso p e número de enrolamento n em um descrição, terá impulso n e número de enrolamento p em a dupla descrição. Por exemplo, a teoria das cordas do tipo IIA é equivalente à teoria das cordas do tipo IIB por meio da dualidade T, e as duas versões da teoria das cordas heteróticas também estão relacionadas pela dualidade T.

Em geral, o termo dualidade refere-se a uma situação em que dois sistemas físicos aparentemente diferentes acabam por ser equivalentes de uma forma não trivial. Duas teorias relacionadas por uma dualidade não precisam ser teorias de cordas. Por exemplo, a dualidade Montonen-Olive é um exemplo de uma relação S-dualidade entre teorias quânticas de campos. A correspondência AdS/CFT é um exemplo de dualidade que relaciona a teoria das cordas a uma teoria quântica de campos. Se duas teorias estão relacionadas por uma dualidade, isso significa que uma teoria pode ser transformada de alguma forma para que acabe se parecendo com a outra teoria. Diz-se então que as duas teorias são duais entre si sob a transformação. Dito de outra forma, as duas teorias são descrições matematicamente diferentes dos mesmos fenômenos.

Branas

Na teoria das cordas e outras teorias relacionadas, uma brana é um objeto físico que generaliza a noção de uma partícula pontual para dimensões superiores. Por exemplo, uma partícula pontual pode ser vista como uma brana de dimensão zero, enquanto uma corda pode ser vista como uma brana de dimensão um. Também é possível considerar branas de dimensões superiores. Na dimensão p, elas são chamadas de p-branas. A palavra brana vem da palavra "membrana" que se refere a uma brana bidimensional.

Branas são objetos dinâmicos que podem se propagar através do espaço-tempo de acordo com as regras da mecânica quântica. Eles têm massa e podem ter outros atributos, como carga. Uma p-brana varre um volume (p+1) dimensional no espaço-tempo chamado volume mundial. Os físicos freqüentemente estudam campos análogos ao campo eletromagnético que reside no volume mundial de uma brana.

Na teoria das cordas, as D-branas são uma classe importante de branas que surgem quando se consideram cordas abertas. À medida que uma corda aberta se propaga através do espaço-tempo, seus pontos finais devem estar em uma D-brana. A letra "D" em D-brana refere-se a uma certa condição matemática no sistema conhecida como condição de contorno de Dirichlet. O estudo das D-branas na teoria das cordas levou a resultados importantes, como a correspondência AdS/CFT, que lançou luz sobre muitos problemas na teoria quântica de campos.

As branas são frequentemente estudadas de um ponto de vista puramente matemático e são descritas como objetos de certas categorias, como a categoria derivada de feixes coerentes em uma variedade algébrica complexa ou a categoria Fukaya de uma variedade simplética. A conexão entre a noção física de uma brana e a noção matemática de uma categoria levou a importantes insights matemáticos nos campos da geometria algébrica e simplética e da teoria da representação.

Teoria M

Antes de 1995, os teóricos acreditavam que havia cinco versões consistentes da teoria das supercordas (tipo I, tipo IIA, tipo IIB e duas versões da teoria das cordas heteróticas). Este entendimento mudou em 1995, quando Edward Witten sugeriu que as cinco teorias eram apenas casos limites especiais de uma teoria onze-dimensional chamada teoria M. A conjectura de Witten foi baseada no trabalho de vários outros físicos, incluindo Ashoke Sen, Chris Hull, Paul Townsend e Michael Duff. Seu anúncio levou a uma onda de atividades de pesquisa agora conhecida como a segunda revolução das supercordas.

Unificação das teorias das supercordas

Na década de 1970, muitos físicos se interessaram pelas teorias da supergravidade, que combinam a relatividade geral com a supersimetria. Enquanto a relatividade geral faz sentido em qualquer número de dimensões, a supergravidade impõe um limite superior ao número de dimensões. Em 1978, o trabalho de Werner Nahm mostrou que a dimensão espaço-temporal máxima na qual se pode formular uma teoria supersimétrica consistente é onze. No mesmo ano, Eugene Cremmer, Bernard Julia e Joël Scherk da École Normale Supérieure mostraram que a supergravidade não só permite até onze dimensões, mas é de facto mais elegante neste número máximo de dimensões.

Inicialmente, muitos físicos esperavam que, ao compactar a supergravidade em onze dimensões, seria possível construir modelos realistas do nosso mundo quadridimensional. A esperança era que tais modelos fornecessem uma descrição unificada das quatro forças fundamentais da natureza: o eletromagnetismo, as forças nucleares fortes e fracas e a gravidade. O interesse na supergravidade onze-dimensional logo diminuiu à medida que várias falhas neste esquema foram descobertas. Um dos problemas era que as leis da física parecem distinguir entre sentido horário e anti-horário, um fenômeno conhecido como quiralidade. Edward Witten e outros observaram que esta propriedade de quiralidade não pode ser facilmente derivada pela compactação de onze dimensões.

Na primeira revolução das supercordas em 1984, muitos físicos recorreram à teoria das cordas como uma teoria unificada da física de partículas e da gravidade quântica. Ao contrário da teoria da supergravidade, a teoria das cordas foi capaz de acomodar a quiralidade do modelo padrão e forneceu uma teoria da gravidade consistente com os efeitos quânticos. Outra característica da teoria das cordas que atraiu muitos físicos nas décadas de 1980 e 1990 foi o seu alto grau de singularidade. Nas teorias de partículas comuns, pode-se considerar qualquer coleção de partículas elementares cujo comportamento clássico é descrito por um Lagrangiano arbitrário. Na teoria das cordas, as possibilidades são muito mais restritas: na década de 1990, os físicos argumentaram que havia apenas cinco versões supersimétricas consistentes da teoria.

Embora houvesse apenas um punhado de teorias consistentes sobre supercordas, permanecia um mistério por que não havia apenas uma formulação consistente. No entanto, à medida que os físicos começaram a examinar mais de perto a teoria das cordas, perceberam que essas teorias estão relacionadas de maneiras intrincadas e não triviais. Eles descobriram que um sistema de cordas com interação forte pode, em alguns casos, ser visto como um sistema de cordas com interação fraca. Este fenômeno é conhecido como S-dualidade. Foi estudado por Ashoke Sen no contexto de cordas heteróticas em quatro dimensões e por Chris Hull e Paul Townsend no contexto da teoria do tipo IIB. Os teóricos também descobriram que diferentes teorias de cordas podem estar relacionadas pela dualidade-T. Esta dualidade implica que as cordas que se propagam em geometrias de espaço-tempo completamente diferentes podem ser fisicamente equivalentes.

Mais ou menos na mesma época, enquanto muitos físicos estudavam as propriedades das cordas, um pequeno grupo de físicos examinava as possíveis aplicações de objetos de dimensões superiores. Em 1987, Eric Bergshoeff, Ergin Sezgin e Paul Townsend mostraram que a supergravidade onze-dimensional inclui branas bidimensionais. Intuitivamente, esses objetos parecem folhas ou membranas que se propagam através do espaço-tempo de onze dimensões. Pouco depois desta descoberta, Michael Duff, Paul Howe, Takeo Inami e Kellogg Stelle consideraram uma compactação particular da supergravidade onze-dimensional com uma das dimensões enrolada num círculo. Neste cenário, pode-se imaginar a membrana envolvendo a dimensão circular. Se o raio do círculo for suficientemente pequeno, então esta membrana se parece com uma corda no espaço-tempo de dez dimensões. Duff e seus colaboradores mostraram que esta construção reproduz exatamente as cordas que aparecem na teoria das supercordas tipo IIA.

Discursando numa conferência sobre teoria de cordas em 1995, Edward Witten fez a surpreendente sugestão de que todas as cinco teorias das supercordas eram, na verdade, apenas diferentes casos limites de uma única teoria em onze dimensões do espaço-tempo. O anúncio de Witten reuniu todos os resultados anteriores sobre a dualidade S e T e o aparecimento de branas de dimensões superiores na teoria das cordas. Nos meses que se seguiram ao anúncio de Witten, centenas de novos artigos apareceram na Internet confirmando diferentes partes da sua proposta. Hoje, essa agitação de trabalho é conhecida como a segunda revolução das supercordas.

Inicialmente, alguns físicos sugeriram que a nova teoria era uma teoria fundamental das membranas, mas Witten era cético quanto ao papel das membranas na teoria. Em um artigo de 1996, Hořava e Witten escreveram “Como foi proposto que a teoria de onze dimensões é uma teoria de supermembrana, mas há algumas razões para duvidar dessa interpretação, nós a chamaremos sem compromisso de teoria M”., deixando para o futuro a relação de M com as membranas." Na ausência de uma compreensão do verdadeiro significado e estrutura da teoria M, Witten sugeriu que o M deveria significar "mágica", "mistério", ou "membrana" de acordo com o gosto, e o verdadeiro significado do título deverá ser decidido quando uma formulação mais fundamental da teoria for conhecida.

Teoria da matriz

Em matemática, uma matriz é uma matriz retangular de números ou outros dados. Na física, um modelo matricial é um tipo particular de teoria física cuja formulação matemática envolve a noção de matriz de uma forma importante. Um modelo matricial descreve o comportamento de um conjunto de matrizes no âmbito da mecânica quântica.

Um exemplo importante de modelo matricial é o modelo matricial BFSS proposto por Tom Banks, Willy Fischler, Stephen Shenker e Leonard Susskind em 1997. Esta teoria descreve o comportamento de um conjunto de nove grandes matrizes. No seu artigo original, estes autores mostraram, entre outras coisas, que o limite de baixa energia deste modelo matricial é descrito pela supergravidade onze-dimensional. Esses cálculos os levaram a propor que o modelo matricial BFSS é exatamente equivalente à teoria M. O modelo matricial BFSS pode, portanto, ser usado como um protótipo para uma formulação correta da teoria M e uma ferramenta para investigar as propriedades da teoria M em um ambiente relativamente simples.

O desenvolvimento da formulação do modelo matricial da teoria M levou os físicos a considerar várias conexões entre a teoria das cordas e um ramo da matemática chamado geometria não comutativa. Este assunto é uma generalização da geometria comum na qual os matemáticos definem novas noções geométricas usando ferramentas da álgebra não comutativa. Em um artigo de 1998, Alain Connes, Michael R. Douglas e Albert Schwarz mostraram que alguns aspectos dos modelos matriciais e da teoria M são descritos por uma teoria quântica de campos não comutativa, um tipo especial de teoria física em que o espaço-tempo é descrito matematicamente usando geometria não comutativa. Isso estabeleceu uma ligação entre os modelos matriciais e a teoria M, por um lado, e a geometria não comutativa, por outro. Rapidamente levou à descoberta de outras ligações importantes entre a geometria não comutativa e várias teorias físicas.

Buracos negros

Na relatividade geral, um buraco negro é definido como uma região do espaço-tempo na qual o campo gravitacional é tão forte que nenhuma partícula ou radiação pode escapar. Nos modelos de evolução estelar actualmente aceites, pensa-se que os buracos negros surgem quando estrelas massivas sofrem colapso gravitacional, e pensa-se que muitas galáxias contêm buracos negros supermassivos nos seus centros. Os buracos negros também são importantes por razões teóricas, pois apresentam desafios profundos para os teóricos que tentam compreender os aspectos quânticos da gravidade. A teoria das cordas provou ser uma ferramenta importante para investigar as propriedades teóricas dos buracos negros porque fornece uma estrutura na qual os teóricos podem estudar a sua termodinâmica.

Fórmula de Bekenstein-Hawking

No ramo da física chamado mecânica estatística, a entropia é uma medida da aleatoriedade ou desordem de um sistema físico. Este conceito foi estudado na década de 1870 pelo físico austríaco Ludwig Boltzmann, que mostrou que as propriedades termodinâmicas de um gás poderiam ser derivadas das propriedades combinadas de suas muitas moléculas constituintes. Boltzmann argumentou que, calculando a média do comportamento de todas as diferentes moléculas de um gás, pode-se compreender propriedades macroscópicas como volume, temperatura e pressão. Além disso, esta perspectiva levou-o a dar uma definição precisa de entropia como o logaritmo natural do número de diferentes estados das moléculas (também chamados de microestados) que dão origem às mesmas características macroscópicas.

No século XX, os físicos começaram a aplicar os mesmos conceitos aos buracos negros. Na maioria dos sistemas, como os gases, a entropia aumenta com o volume. Na década de 1970, o físico Jacob Bekenstein sugeriu que a entropia de um buraco negro é, em vez disso, proporcional à área de superfície do seu horizonte de eventos, a fronteira além da qual a matéria e a radiação são perdidas devido à sua atração gravitacional. Quando combinado com as ideias do físico Stephen Hawking, o trabalho de Bekenstein produziu uma fórmula precisa para a entropia de um buraco negro. A fórmula de Bekenstein-Hawking expressa a entropia S como

${displaystyle S={frac {c^{3}kA}{4hbar G.$

onde c é a velocidade da luz, k é a constante de Boltzmann, ħ é a constante de Planck reduzida, G é a constante de Newton e A é a área da superfície do horizonte de eventos.

Como qualquer sistema físico, um buraco negro tem uma entropia definida em termos do número de microestados diferentes que levam às mesmas características macroscópicas. A fórmula de entropia de Bekenstein-Hawking fornece o valor esperado da entropia de um buraco negro, mas na década de 1990, os físicos ainda não tinham uma derivação desta fórmula contando microestados em uma teoria da gravidade quântica. Encontrar tal derivação desta fórmula foi considerado um teste importante da viabilidade de qualquer teoria da gravidade quântica, como a teoria das cordas.

Derivação na teoria das cordas

Em um artigo de 1996, Andrew Strominger e Cumrun Vafa mostraram como derivar a fórmula de Beckenstein-Hawking para certos buracos negros na teoria das cordas. O seu cálculo baseou-se na observação de que as D-branas – que se parecem com membranas flutuantes quando interagem fracamente – tornam-se objetos densos e massivos com horizontes de eventos quando as interações são fortes. Em outras palavras, um sistema de D-branas fortemente interagindo na teoria das cordas é indistinguível de um buraco negro. Strominger e Vafa analisaram esses sistemas de D-branas e calcularam o número de maneiras diferentes de colocar D-branas no espaço-tempo, de modo que sua massa e carga combinadas fossem iguais a uma determinada massa e carga para o buraco negro resultante. Seu cálculo reproduziu exatamente a fórmula de Bekenstein-Hawking, incluindo o fator de 1/4. Trabalhos subsequentes de Strominger, Vafa e outros refinaram os cálculos originais e forneceram os valores precisos das "correções quânticas" necessário para descrever buracos negros muito pequenos.

Os buracos negros que Strominger e Vafa consideraram no seu trabalho original eram bastante diferentes dos buracos negros astrofísicos reais. Uma diferença foi que Strominger e Vafa consideraram apenas buracos negros extremos para tornar o cálculo tratável. Estes são definidos como buracos negros com a menor massa possível compatível com uma determinada carga. Strominger e Vafa também restringiram a atenção aos buracos negros no espaço-tempo pentadimensional com supersimetria não física.

Embora tenha sido originalmente desenvolvido neste contexto muito particular e fisicamente irrealista da teoria das cordas, o cálculo da entropia de Strominger e Vafa levou a uma compreensão qualitativa de como a entropia do buraco negro pode ser explicada em qualquer teoria da gravidade quântica. Na verdade, em 1998, Strominger argumentou que o resultado original poderia ser generalizado para uma teoria arbitrária e consistente da gravidade quântica sem depender de cordas ou supersimetria. Em colaboração com vários outros autores, em 2010, ele mostrou que alguns resultados sobre a entropia dos buracos negros poderiam ser estendidos a buracos negros astrofísicos não extremos.

Correspondência AdS/CFT

Uma abordagem para formular a teoria das cordas e estudar suas propriedades é fornecida pela correspondência anti-de Sitter/teoria de campo conforme (AdS/CFT). Este é um resultado teórico que implica que a teoria das cordas é, em alguns casos, equivalente a uma teoria quântica de campos. Além de fornecer insights sobre a estrutura matemática da teoria das cordas, a correspondência AdS/CFT lançou luz sobre muitos aspectos da teoria quântica de campos em regimes onde as técnicas de cálculo tradicionais são ineficazes. A correspondência AdS/CFT foi proposta pela primeira vez por Juan Maldacena no final de 1997. Aspectos importantes da correspondência foram elaborados em artigos de Steven Gubser, Igor Klebanov e Alexander Markovich Polyakov, e de Edward Witten. Em 2010, o artigo de Maldacena teve mais de 7.000 citações, tornando-se o artigo mais citado na área de física de altas energias.

Visão geral da correspondência

Na correspondência AdS/CFT, a geometria do espaço-tempo é descrita em termos de uma certa solução de vácuo da equação de Einstein chamada espaço anti-de Sitter. Em termos muito elementares, o espaço anti-de Sitter é um modelo matemático do espaço-tempo no qual a noção de distância entre pontos (a métrica) é diferente da noção de distância na geometria euclidiana comum. Está intimamente relacionado ao espaço hiperbólico, que pode ser visto como um disco conforme ilustrado à esquerda. Esta imagem mostra um mosaico de um disco por triângulos e quadrados. Pode-se definir a distância entre os pontos deste disco de tal forma que todos os triângulos e quadrados tenham o mesmo tamanho e o limite externo circular esteja infinitamente distante de qualquer ponto no interior.

Pode-se imaginar uma pilha de discos hiperbólicos onde cada disco representa o estado do universo em um determinado momento. O objeto geométrico resultante é um espaço anti-de Sitter tridimensional. Parece um cilindro sólido no qual qualquer seção transversal é uma cópia do disco hiperbólico. O tempo corre na direção vertical nesta imagem. A superfície deste cilindro desempenha um papel importante na correspondência AdS/CFT. Tal como acontece com o plano hiperbólico, o espaço anti-de Sitter é curvado de tal forma que qualquer ponto no interior está, na verdade, infinitamente longe desta superfície limite.

Esta construção descreve um universo hipotético com apenas duas dimensões espaciais e uma dimensão temporal, mas pode ser generalizado para qualquer número de dimensões. Na verdade, o espaço hiperbólico pode ter mais de duas dimensões e pode-se "empilhar" cópias do espaço hiperbólico para obter modelos de dimensões superiores do espaço anti-de Sitter.

Uma característica importante do espaço anti-de Sitter é o seu limite (que se parece com um cilindro no caso do espaço anti-de Sitter tridimensional). Uma propriedade desta fronteira é que, dentro de uma pequena região da superfície em torno de qualquer ponto, ela se parece exatamente com o espaço de Minkowski, o modelo de espaço-tempo usado na física não gravitacional. Pode-se, portanto, considerar uma teoria auxiliar na qual o "espaço-tempo" é dado pelo limite do espaço anti-de Sitter. Esta observação é o ponto de partida para a correspondência AdS/CFT, que afirma que a fronteira do espaço anti-de Sitter pode ser considerada como o "espaço-tempo" para uma teoria quântica de campos. A alegação é que esta teoria quântica de campos é equivalente a uma teoria gravitacional, como a teoria das cordas, no espaço anti-de Sitter, no sentido de que existe um "dicionário" para traduzir entidades e cálculos de uma teoria em suas contrapartes na outra teoria. Por exemplo, uma única partícula na teoria gravitacional pode corresponder a algum conjunto de partículas na teoria dos limites. Além disso, as previsões nas duas teorias são quantitativamente idênticas, de modo que se duas partículas têm 40% de probabilidade de colidir na teoria gravitacional, então as coleções correspondentes na teoria dos limites também teriam 40% de probabilidade de colidir.

Aplicações à gravidade quântica

A descoberta da correspondência AdS/CFT foi um grande avanço na ciência dos físicos. compreensão da teoria das cordas e da gravidade quântica. Uma razão para isso é que a correspondência fornece uma formulação da teoria das cordas em termos da teoria quântica de campos, que é bem compreendida por comparação. Outra razão é que fornece uma estrutura geral na qual os físicos podem estudar e tentar resolver os paradoxos dos buracos negros.

Em 1975, Stephen Hawking publicou um cálculo que sugeria que os buracos negros não são completamente negros, mas emitem uma radiação fraca devido a efeitos quânticos perto do horizonte de eventos. No início, o resultado de Hawking representou um problema para os teóricos porque sugeria que os buracos negros destroem informação. Mais precisamente, o cálculo de Hawking parecia entrar em conflito com um dos postulados básicos da mecânica quântica, que afirma que os sistemas físicos evoluem no tempo de acordo com a equação de Schrödinger. Esta propriedade é geralmente referida como unitariedade da evolução temporal. A aparente contradição entre o cálculo de Hawking e o postulado da unitariedade da mecânica quântica ficou conhecida como o paradoxo da informação do buraco negro.

A correspondência AdS/CFT resolve o paradoxo da informação do buraco negro, pelo menos até certo ponto, porque mostra como um buraco negro pode evoluir de uma maneira consistente com a mecânica quântica em alguns contextos. Na verdade, pode-se considerar buracos negros no contexto da correspondência AdS/CFT, e qualquer buraco negro corresponde a uma configuração de partículas na fronteira do espaço anti-de Sitter. Estas partículas obedecem às regras habituais da mecânica quântica e em particular evoluem de forma unitária, pelo que o buraco negro também deve evoluir de forma unitária, respeitando os princípios da mecânica quântica. Em 2005, Hawking anunciou que o paradoxo tinha sido resolvido em favor da conservação da informação pela correspondência AdS/CFT, e sugeriu um mecanismo concreto pelo qual os buracos negros poderiam preservar a informação.

Aplicações à física nuclear

Além de suas aplicações a problemas teóricos em gravidade quântica, a correspondência AdS/CFT tem sido aplicada a uma variedade de problemas em teoria quântica de campos. Um sistema físico que foi estudado usando a correspondência AdS/CFT é o plasma quark-glúon, um estado exótico da matéria produzido em aceleradores de partículas. Este estado da matéria surge por breves instantes quando íons pesados, como ouro ou núcleos de chumbo, colidem em altas energias. Essas colisões fazem com que os quarks que compõem os núcleos atômicos sejam desconfinados a temperaturas de aproximadamente dois trilhões de Kelvin, condições semelhantes às presentes em cerca de 10⁻¹¹ segundos. depois do Big Bang.

A física do plasma quark-glúon é governada por uma teoria chamada cromodinâmica quântica, mas esta teoria é matematicamente intratável em problemas que envolvem o plasma quark-glúon. Num artigo publicado em 2005, Đàm Thanh Sơn e os seus colaboradores mostraram que a correspondência AdS/CFT poderia ser usada para compreender alguns aspectos do plasma de quark-glúon, descrevendo-o na linguagem da teoria das cordas. Ao aplicar a correspondência AdS/CFT, Sơn e seus colaboradores foram capazes de descrever o plasma de quark-gluon em termos de buracos negros no espaço-tempo pentadimensional. O cálculo mostrou que a proporção de duas quantidades associadas ao plasma de quark-glúon, a viscosidade de cisalhamento e a densidade volumétrica de entropia, deveria ser aproximadamente igual a uma certa constante universal. Em 2008, o valor previsto desta relação para o plasma quark-glúon foi confirmado no Colisor Relativístico de Íons Pesados no Laboratório Nacional de Brookhaven.

Aplicações à física da matéria condensada

A correspondência AdS/CFT também tem sido usada para estudar aspectos da física da matéria condensada. Ao longo das décadas, os físicos experimentais da matéria condensada descobriram uma série de estados exóticos da matéria, incluindo supercondutores e superfluidos. Esses estados são descritos usando o formalismo da teoria quântica de campos, mas alguns fenômenos são difíceis de explicar usando técnicas padrão de teoria de campos. Alguns teóricos da matéria condensada, incluindo Subir Sachdev, esperam que a correspondência AdS/CFT torne possível descrever estes sistemas na linguagem da teoria das cordas e aprender mais sobre o seu comportamento.

Até agora, algum sucesso foi alcançado no uso de métodos da teoria das cordas para descrever a transição de um superfluido para um isolante. Um superfluido é um sistema de átomos eletricamente neutros que flui sem qualquer atrito. Tais sistemas são frequentemente produzidos em laboratório utilizando hélio líquido, mas recentemente experimentalistas desenvolveram novas formas de produzir superfluidos artificiais, despejando triliões de átomos frios numa rede de lasers entrecruzados. Esses átomos inicialmente se comportam como um superfluido, mas à medida que os experimentalistas aumentam a intensidade dos lasers, eles se tornam menos móveis e, de repente, passam para um estado isolante. Durante a transição, os átomos se comportam de maneira incomum. Por exemplo, os átomos desaceleram até parar a uma taxa que depende da temperatura e da constante de Planck, parâmetro fundamental da mecânica quântica, que não entra na descrição das outras fases. Este comportamento foi recentemente compreendido considerando uma descrição dupla onde as propriedades do fluido são descritas em termos de um buraco negro de dimensão superior.

Fenomenologia

Além de ser uma ideia de considerável interesse teórico, a teoria das cordas fornece uma estrutura para a construção de modelos da física do mundo real que combinam a relatividade geral e a física de partículas. A fenomenologia é o ramo da física teórica em que os físicos constroem modelos realistas da natureza a partir de ideias teóricas mais abstratas. A fenomenologia das cordas é a parte da teoria das cordas que tenta construir modelos realistas ou semi-realistas baseados na teoria das cordas.

Em parte devido a dificuldades teóricas e matemáticas e em parte devido às energias extremamente elevadas necessárias para testar experimentalmente estas teorias, não há até agora nenhuma evidência experimental que aponte inequivocamente que qualquer um destes modelos seja uma descrição fundamental correta da natureza. Isto levou alguns membros da comunidade a criticar estas abordagens à unificação e a questionar o valor da investigação contínua sobre estes problemas.

Física de partículas

A teoria atualmente aceita que descreve partículas elementares e suas interações é conhecida como modelo padrão da física de partículas. Esta teoria fornece uma descrição unificada de três das forças fundamentais da natureza: o eletromagnetismo e as forças nucleares forte e fraca. Apesar do seu notável sucesso na explicação de uma vasta gama de fenómenos físicos, o modelo padrão não pode ser uma descrição completa da realidade. Isto ocorre porque o modelo padrão não incorpora a força da gravidade e devido a problemas como o problema da hierarquia e a incapacidade de explicar a estrutura das massas dos férmions ou da matéria escura.

A teoria das cordas tem sido usada para construir uma variedade de modelos de física de partículas que vão além do modelo padrão. Normalmente, tais modelos são baseados na ideia de compactação. Começando com o espaço-tempo de dez ou onze dimensões das cordas ou da teoria M, os físicos postulam uma forma para as dimensões extras. Ao escolher esta forma apropriadamente, eles podem construir modelos aproximadamente semelhantes ao modelo padrão da física de partículas, juntamente com partículas adicionais não descobertas. Uma maneira popular de derivar a física realista da teoria das cordas é começar com a teoria heterótica em dez dimensões e assumir que as seis dimensões extras do espaço-tempo têm a forma de uma variedade Calabi-Yau hexadimensional. Tais compactações oferecem muitas maneiras de extrair a física realista da teoria das cordas. Outros métodos semelhantes podem ser usados para construir modelos realistas ou semi-realistas do nosso mundo quadridimensional com base na teoria M.

Cosmologia

A teoria do Big Bang é o modelo cosmológico predominante para o universo desde os primeiros períodos conhecidos até sua subsequente evolução em grande escala. Apesar do seu sucesso na explicação de muitas características observadas no Universo, incluindo os desvios para o vermelho galácticos, a abundância relativa de elementos leves, como o hidrogénio e o hélio, e a existência de uma radiação cósmica de fundo em micro-ondas, existem várias questões que permanecem sem resposta. Por exemplo, o modelo padrão do Big Bang não explica porque é que o Universo parece ser o mesmo em todas as direcções, porque é que parece plano em escalas de distância muito grandes, ou porque é que certas partículas hipotéticas, como os monopolos magnéticos, não são observadas em experiências.

Atualmente, a principal candidata a uma teoria que vai além do Big Bang é a teoria da inflação cósmica. Desenvolvida por Alan Guth e outros na década de 1980, a inflação postula um período de expansão extremamente rápida e acelerada do universo antes da expansão descrita pela teoria padrão do Big Bang. A teoria da inflação cósmica preserva os sucessos do Big Bang, ao mesmo tempo que fornece uma explicação natural para algumas das características misteriosas do universo. A teoria também recebeu um apoio surpreendente de observações da radiação cósmica de fundo em micro-ondas, a radiação que preenche o céu cerca de 380 mil anos após o Big Bang.

Na teoria da inflação, a rápida expansão inicial do universo é causada por uma partícula hipotética chamada ínflaton. As propriedades exatas desta partícula não são fixadas pela teoria, mas deveriam, em última análise, ser derivadas de uma teoria mais fundamental, como a teoria das cordas. Na verdade, tem havido uma série de tentativas de identificar um ínflaton dentro do espectro de partículas descrito pela teoria das cordas e de estudar a inflação usando a teoria das cordas. Embora essas abordagens possam eventualmente encontrar apoio em dados observacionais, como medições da radiação cósmica de fundo em micro-ondas, a aplicação da teoria das cordas à cosmologia ainda está em seus estágios iniciais.

Conexões com a matemática

Além de influenciar a pesquisa em física teórica, a teoria das cordas estimulou uma série de desenvolvimentos importantes na matemática pura. Como muitas ideias em desenvolvimento na física teórica, a teoria das cordas não possui atualmente uma formulação matematicamente rigorosa na qual todos os seus conceitos possam ser definidos com precisão. Como resultado, os físicos que estudam a teoria das cordas são frequentemente guiados pela intuição física para conjecturar relações entre as estruturas matemáticas aparentemente diferentes que são usadas para formalizar diferentes partes da teoria. Estas conjecturas são posteriormente provadas por matemáticos e, desta forma, a teoria das cordas serve como fonte de novas ideias em matemática pura.

Simetria de espelho

Depois que as variedades Calabi-Yau entraram na física como uma forma de compactar dimensões extras na teoria das cordas, muitos físicos começaram a estudar essas variedades. No final da década de 1980, vários físicos notaram que, dada tal compactação da teoria das cordas, não é possível reconstruir exclusivamente uma variedade Calabi-Yau correspondente. Em vez disso, duas versões diferentes da teoria das cordas, tipo IIA e tipo IIB, podem ser compactadas em variedades Calabi-Yau completamente diferentes, dando origem à mesma física. Nesta situação, as variedades são chamadas de variedades de espelho, e a relação entre as duas teorias físicas é chamada de simetria de espelho.

Independentemente de as compactações Calabi-Yau da teoria das cordas fornecerem uma descrição correta da natureza, a existência da dualidade espelhada entre as diferentes teorias das cordas tem consequências matemáticas significativas. As variedades Calabi-Yau usadas na teoria das cordas são de interesse na matemática pura, e a simetria espelhada permite que os matemáticos resolvam problemas em geometria enumerativa, um ramo da matemática preocupado em contar o número de soluções para questões geométricas.

A geometria enumerativa estuda uma classe de objetos geométricos chamados variedades algébricas que são definidas pelo desaparecimento de polinômios. Por exemplo, a cúbica de Clebsch ilustrada à direita é uma variedade algébrica definida usando um certo polinômio de grau três em quatro variáveis. Um célebre resultado dos matemáticos do século XIX, Arthur Cayley e George Salmon, afirma que existem exatamente 27 linhas retas inteiramente sobre tal superfície.

Generalizando este problema, pode-se perguntar quantas linhas podem ser desenhadas em uma variedade quíntica de Calabi-Yau, como a ilustrada acima, que é definida por um polinômio de grau cinco. Este problema foi resolvido pelo matemático alemão do século XIX, Hermann Schubert, que descobriu que existem exatamente 2.875 dessas linhas. Em 1986, o geômetra Sheldon Katz provou que o número de curvas, como círculos, definidas por polinômios de grau dois e situadas inteiramente no quíntico é 609.250.

No ano de 1991, a maioria dos problemas clássicos da geometria enumerativa foram resolvidos e o interesse pela geometria enumerativa começou a diminuir. O campo foi revigorado em maio de 1991, quando os físicos Philip Candelas, Xenia de la Ossa, Paul Green e Linda Parks mostraram que a simetria do espelho poderia ser usada para traduzir questões matemáticas difíceis sobre uma variedade Calabi-Yau em questões mais fáceis sobre seu espelho. Em particular, eles usaram simetria de espelho para mostrar que uma variedade Calabi-Yau hexadimensional pode conter exatamente 317.206.375 curvas de grau três. Além de contar curvas de grau três, Candelas e seus colaboradores obtiveram uma série de resultados mais gerais para a contagem de curvas racionais que iam muito além dos resultados obtidos pelos matemáticos.

Originalmente, estes resultados de Candelas foram justificados por motivos físicos. Contudo, os matemáticos geralmente preferem provas rigorosas que não exijam um apelo à intuição física. Inspirado em físicos & # 39; Ao trabalhar na simetria do espelho, os matemáticos construíram, portanto, seus próprios argumentos provando as previsões enumerativas da simetria do espelho. Hoje, a simetria do espelho é uma área ativa de pesquisa em matemática, e os matemáticos estão trabalhando para desenvolver uma compreensão matemática mais completa da simetria do espelho com base nas pesquisas dos físicos. intuição. As principais abordagens para a simetria de espelho incluem o programa de simetria de espelho homológica de Maxim Kontsevich e a conjectura SYZ de Andrew Strominger, Shing-Tung Yau e Eric Zaslow.

Luar monstruoso

A teoria dos grupos é o ramo da matemática que estuda o conceito de simetria. Por exemplo, pode-se considerar uma forma geométrica como um triângulo equilátero. Existem várias operações que podem ser realizadas neste triângulo sem alterar sua forma. Pode-se girá-lo 120°, 240° ou 360°, ou pode-se refletir em qualquer uma das linhas rotuladas S₀< /span>, S₁ ou S ₂ na imagem. Cada uma dessas operações é chamada de simetria, e o conjunto dessas simetrias satisfaz certas propriedades técnicas, formando o que os matemáticos chamam de grupo. Neste exemplo específico, o grupo é conhecido como grupo diédrico de ordem 6 porque possui seis elementos. Um grupo geral pode descrever um número finito ou infinito de simetrias; se houver apenas um número finito de simetrias, ele é chamado de grupo finito.

Os matemáticos muitas vezes se esforçam para obter uma classificação (ou lista) de todos os objetos matemáticos de um determinado tipo. Acredita-se geralmente que os grupos finitos são demasiado diversos para admitir uma classificação útil. Um problema mais modesto, mas ainda desafiador, é classificar todos os grupos simples finitos. Estes são grupos finitos que podem ser usados como blocos de construção para a construção de grupos finitos arbitrários, da mesma forma que os números primos podem ser usados para construir números inteiros arbitrários tomando produtos. Uma das principais conquistas da teoria de grupos contemporânea é a classificação de grupos simples finitos, um teorema matemático que fornece uma lista de todos os grupos simples finitos possíveis.

Este teorema de classificação identifica várias famílias infinitas de grupos, bem como 26 grupos adicionais que não cabem em nenhuma família. Os últimos grupos são chamados de grupos "esporádicos" grupos, e cada um deve a sua existência a uma notável combinação de circunstâncias. O maior grupo esporádico, o chamado grupo monstro, tem mais de 10⁵³ elementos, mais de mil vezes o número de átomos da Terra.

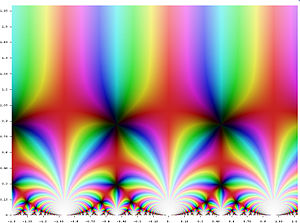
Uma construção aparentemente não relacionada é a função j da teoria dos números. Este objeto pertence a uma classe especial de funções chamadas funções modulares, cujos gráficos formam um certo tipo de padrão de repetição. Embora esta função apareça num ramo da matemática que parece muito diferente da teoria dos grupos finitos, os dois assuntos revelam-se intimamente relacionados. No final da década de 1970, os matemáticos John McKay e John Thompson notaram que certos números que surgem na análise do grupo de monstros (ou seja, as dimensões das suas representações irredutíveis) estão relacionados com números que aparecem numa fórmula para o j (ou seja, os coeficientes de sua série de Fourier). Esse relacionamento foi desenvolvido por John Horton Conway e Simon Norton, que o chamaram de luar monstruoso porque parecia tão improvável.

Em 1992, Richard Borcherds construiu uma ponte entre a teoria das funções modulares e dos grupos finitos e, no processo, explicou as observações de McKay e Thompson. Borcherds' O trabalho usou ideias da teoria das cordas de uma forma essencial, estendendo resultados anteriores de Igor Frenkel, James Lepowsky e Arne Meurman, que perceberam o grupo monstro como as simetrias de uma versão particular da teoria das cordas. Em 1998, Borcherds recebeu a medalha Fields por seu trabalho.

Desde a década de 1990, a conexão entre a teoria das cordas e o luar levou a novos resultados em matemática e física. Em 2010, os físicos Tohru Eguchi, Hirosi Ooguri e Yuji Tachikawa descobriram conexões entre um grupo esporádico diferente, o grupo Mathieu M24, e uma certa versão da teoria das cordas. Miranda Cheng, John Duncan e Jeffrey A. Harvey propuseram uma generalização desse fenômeno de luar chamado luar umbral, e sua conjectura foi provada matematicamente por Duncan, Michael Griffin e Ken Ono. Witten também especulou que a versão da teoria das cordas que aparece na lua monstruosa pode estar relacionada a um certo modelo simplificado de gravidade em três dimensões do espaço-tempo.

Histórico

Resultados iniciais

Algumas das estruturas reintroduzidas pela teoria das cordas surgiram pela primeira vez muito antes, como parte do programa de unificação clássica iniciado por Albert Einstein. A primeira pessoa a adicionar uma quinta dimensão a uma teoria da gravidade foi Gunnar Nordström em 1914, que observou que a gravidade em cinco dimensões descreve tanto a gravidade quanto o eletromagnetismo em quatro. Nordström tentou unificar o eletromagnetismo com sua teoria da gravitação, que foi, no entanto, substituída pela relatividade geral de Einstein em 1919. Posteriormente, o matemático alemão Theodor Kaluza combinou a quinta dimensão com a relatividade geral, e apenas Kaluza é geralmente creditado com a ideia. Em 1926, o físico sueco Oskar Klein deu uma interpretação física da dimensão extra inobservável – ela está envolvida num pequeno círculo. Einstein introduziu um tensor métrico não simétrico, enquanto muito mais tarde Brans e Dicke adicionaram um componente escalar à gravidade. Essas ideias seriam revividas na teoria das cordas, onde são exigidas pelas condições de consistência.

A teoria das cordas foi originalmente desenvolvida durante o final da década de 1960 e início da década de 1970 como uma teoria dos hádrons, que nunca foi totalmente bem-sucedida, as partículas subatômicas como o próton e o nêutron que sentem a forte interação. Na década de 1960, Geoffrey Chew e Steven Frautschi descobriram que os mésons formam famílias chamadas trajetórias Regge com massas relacionadas a spins de uma forma que mais tarde foi entendida por Yoichiro Nambu, Holger Bech Nielsen e Leonard Susskind como sendo a relação esperada das cordas rotativas. Chew defendeu a elaboração de uma teoria para as interações dessas trajetórias que não presumisse que elas fossem compostas de quaisquer partículas fundamentais, mas que construísse suas interações a partir de condições de autoconsistência na matriz S. A abordagem da matriz S foi iniciada por Werner Heisenberg na década de 1940 como uma forma de construir uma teoria que não se baseasse nas noções locais de espaço e tempo, que Heisenberg acreditava falharem na escala nuclear. Embora a escala estivesse fora de escala em muitas ordens de magnitude, a abordagem que ele defendia era idealmente adequada para uma teoria da gravidade quântica.

Trabalhando com dados experimentais, R. Dolen, D. Horn e C. Schmid desenvolveram algumas regras de soma para troca de hádrons. Quando uma partícula e uma antipartícula se dispersam, as partículas virtuais podem ser trocadas de duas maneiras qualitativamente diferentes. No canal s, as duas partículas se aniquilam para formar estados intermediários temporários que se desintegram nas partículas do estado final. No canal t, as partículas trocam estados intermediários por emissão e absorção. Na teoria de campo, as duas contribuições se somam, uma dando uma contribuição de fundo contínua, a outra dando picos em certas energias. Nos dados, ficou claro que os picos estavam roubando do fundo – os autores interpretaram isso como dizendo que a contribuição do canal t era dupla em relação à do canal s, o que significa que ambos descreviam toda a amplitude e incluíam o outro.

O resultado foi amplamente divulgado por Murray Gell-Mann, levando Gabriele Veneziano a construir uma amplitude de espalhamento que tinha a propriedade da dualidade Dolen-Horn-Schmid, mais tarde renomeada como dualidade de folha de mundo. A amplitude precisava de pólos onde as partículas aparecem, em trajetórias retilíneas, e há uma função matemática especial cujos pólos estão uniformemente espaçados na metade da linha real – a função gama – que foi amplamente utilizada na teoria de Regge. Ao manipular combinações de funções gama, Veneziano conseguiu encontrar uma amplitude de espalhamento consistente com pólos em linhas retas, com resíduos em sua maioria positivos, que obedecesse à dualidade e tivesse a escala de Regge apropriada em alta energia. A amplitude poderia ajustar-se a dados de espalhamento de feixe próximo, bem como outros ajustes do tipo Regge e tinha uma representação integral sugestiva que poderia ser usada para generalização.

Nos anos seguintes, centenas de físicos trabalharam para completar o programa bootstrap deste modelo, com muitas surpresas. O próprio Veneziano descobriu que para a amplitude de espalhamento descrever o espalhamento de uma partícula que aparece na teoria, uma condição óbvia de autoconsistência, a partícula mais leve deve ser um táquion. Miguel Virasoro e Joel Shapiro encontraram uma amplitude diferente agora entendida como a de cordas fechadas, enquanto Ziro Koba e Holger Nielsen generalizaram a representação integral de Veneziano para o espalhamento multipartículas. Veneziano e Sergio Fubini introduziram um formalismo de operador para calcular as amplitudes de espalhamento que foi um precursor da teoria conformada da folha mundial, enquanto Virasoro entendeu como remover os pólos com resíduos de sinais errados usando uma restrição nos estados. Claud Lovelace calculou uma amplitude de loop e observou que há uma inconsistência, a menos que a dimensão da teoria seja 26. Charles Thorn, Peter Goddard e Richard Brower provaram que não existem estados de propagação de sinais errados em dimensões menores ou iguais para 26.

Em 1969-70, Yoichiro Nambu, Holger Bech Nielsen e Leonard Susskind reconheceram que a teoria poderia receber uma descrição no espaço e no tempo em termos de cordas. As amplitudes de espalhamento foram derivadas sistematicamente do princípio de ação de Peter Goddard, Jeffrey Goldstone, Claudio Rebbi e Charles Thorn, dando uma imagem espaço-temporal aos operadores de vértice introduzidos por Veneziano e Fubini e uma interpretação geométrica às condições de Virasoro.

Em 1971, Pierre Ramond adicionou férmions ao modelo, o que o levou a formular uma supersimetria bidimensional para cancelar os estados de sinais errados. John Schwarz e André Neveu acrescentaram outro setor à teoria de Fermi pouco tempo depois. Nas teorias do férmion, a dimensão crítica era 10. Stanley Mandelstam formulou uma teoria conformada da folha mundial para o caso Bose e Fermi, fornecendo um caminho teórico de campo bidimensional integral para gerar o formalismo do operador. Michio Kaku e Keiji Kikkawa deram uma formulação diferente da corda bosônica, como uma teoria de campo de cordas, com infinitos tipos de partículas e com campos assumindo valores não em pontos, mas em loops e curvas.

Em 1974, Tamiaki Yoneya descobriu que todas as teorias de cordas conhecidas incluíam uma partícula sem massa de spin dois que obedecia às identidades corretas de Ward para ser um gráviton. John Schwarz e Joël Scherk chegaram à mesma conclusão e deram o ousado salto ao sugerir que a teoria das cordas era uma teoria da gravidade, não uma teoria dos hádrons. Eles reintroduziram a teoria Kaluza-Klein como uma forma de dar sentido às dimensões extras. Ao mesmo tempo, a cromodinâmica quântica foi reconhecida como a teoria correta dos hádrons, desviando a atenção dos físicos e aparentemente deixando o programa bootstrap na lata de lixo da história.

A teoria das cordas acabou saindo da lata de lixo, mas na década seguinte todo o trabalho sobre a teoria foi completamente ignorado. Ainda assim, a teoria continuou a desenvolver-se a um ritmo constante graças ao trabalho de um punhado de devotos. Ferdinando Gliozzi, Joël Scherk e David Olive perceberam em 1977 que as cordas originais de Ramond e Neveu Schwarz eram separadamente inconsistentes e precisavam ser combinadas. A teoria resultante não tinha táquion e foi comprovado que tinha supersimetria espaço-tempo por John Schwarz e Michael Green em 1984. No mesmo ano, Alexander Polyakov deu à teoria uma formulação moderna de integral de caminho e passou a desenvolver extensivamente a teoria de campo conforme. Em 1979, Daniel Friedan mostrou que as equações de movimentos da teoria das cordas, que são generalizações das equações de Einstein da relatividade geral, emergem das equações do grupo de renormalização para a teoria de campo bidimensional. Schwarz e Green descobriram a dualidade T e construíram duas teorias de supercordas - IIA e IIB relacionadas pela dualidade T e teorias do tipo I com cordas abertas. As condições de consistência foram tão fortes que toda a teoria foi determinada de forma quase única, com apenas algumas escolhas discretas.

Primeira revolução das supercordas

No início da década de 1980, Edward Witten descobriu que a maioria das teorias da gravidade quântica não conseguia acomodar férmions quirais como o neutrino. Isto o levou, em colaboração com Luis Álvarez-Gaumé, a estudar as violações das leis de conservação nas teorias da gravidade com anomalias, concluindo que as teorias das cordas do tipo I eram inconsistentes. Green e Schwarz descobriram uma contribuição para a anomalia que Witten e Alvarez-Gaumé não perceberam, que restringia o grupo de calibre da teoria das cordas tipo I a SO(32). Ao compreender esse cálculo, Edward Witten convenceu-se de que a teoria das cordas era realmente uma teoria consistente da gravidade e tornou-se um defensor de destaque. Seguindo o exemplo de Witten, entre 1984 e 1986, centenas de físicos começaram a trabalhar neste campo, e isto é por vezes chamado de a primeira revolução das supercordas.

Durante este período, David Gross, Jeffrey Harvey, Emil Martinec e Ryan Rohm descobriram cordas heteróticas. O grupo de medidores dessas cordas fechadas era duas cópias do E8, e qualquer uma das cópias poderia incluir fácil e naturalmente o modelo padrão. Philip Candelas, Gary Horowitz, Andrew Strominger e Edward Witten descobriram que as variedades Calabi-Yau são as compactificações que preservam uma quantidade realista de supersimetria, enquanto Lance Dixon e outros trabalharam nas propriedades físicas dos orbifolds, singularidades geométricas distintas permitidas na teoria das cordas. Cumrun Vafa generalizou a dualidade T de círculos para variedades arbitrárias, criando o campo matemático da simetria do espelho. Daniel Friedan, Emil Martinec e Stephen Shenker desenvolveram ainda mais a quantização covariante da supercorda usando técnicas de teoria de campo conforme. David Gross e Vipul Periwal descobriram que a teoria da perturbação das cordas era divergente. Stephen Shenker mostrou que ela divergiu muito mais rápido do que na teoria de campo, sugerindo que faltavam novos objetos não perturbativos.

Na década de 1990, Joseph Polchinski descobriu que a teoria requer objetos de dimensões superiores, chamados D-branas, e identificou-os com as soluções da supergravidade dos buracos negros. Estes foram entendidos como os novos objetos sugeridos pelas divergências perturbativas e abriram um novo campo com uma rica estrutura matemática. Rapidamente ficou claro que D-branas e outras p-branas, e não apenas cordas, formavam o conteúdo de matéria das teorias das cordas, e a interpretação física das cordas e branas foi revelada – elas são um tipo de buraco negro. Leonard Susskind incorporou o princípio holográfico de Gerardus 't Hooft na teoria das cordas, identificando os longos estados das cordas altamente excitados com os estados térmicos comuns dos buracos negros. Conforme sugerido por 't Hooft, as flutuações do horizonte do buraco negro, a teoria do lençol mundial ou do volume mundial, descrevem não apenas os graus de liberdade do buraco negro, mas também de todos os objetos próximos.

Segunda revolução das supercordas

Em 1995, na conferência anual de teóricos de cordas da Universidade do Sul da Califórnia (USC), Edward Witten fez um discurso sobre a teoria das cordas que, em essência, uniu as cinco teorias de cordas que existiam na época, e deu origem a uma nova teoria de 11 dimensões chamada teoria M. A teoria M também foi prenunciada no trabalho de Paul Townsend aproximadamente na mesma época. A agitação que começou nessa época é às vezes chamada de segunda revolução das supercordas.

Durante este período, Tom Banks, Willy Fischler, Stephen Shenker e Leonard Susskind formularam a teoria da matriz, uma descrição holográfica completa da teoria M usando branas IIA D0. Esta foi a primeira definição da teoria das cordas totalmente não perturbativa e uma realização matemática concreta do princípio holográfico. É um exemplo de dualidade calibre-gravidade e agora é entendido como um caso especial da correspondência AdS/CFT. Andrew Strominger e Cumrun Vafa calcularam a entropia de certas configurações de D-branas e encontraram concordância com a resposta semiclássica para buracos negros com carga extrema. Petr Hořava e Witten encontraram a formulação onze-dimensional das teorias das cordas heteróticas, mostrando que orbifolds resolvem o problema da quiralidade. Witten observou que a descrição eficaz da física das D-branas em baixas energias é feita por uma teoria de calibre supersimétrica, e encontrou interpretações geométricas de estruturas matemáticas na teoria de calibre que ele e Nathan Seiberg haviam descoberto anteriormente em termos da localização das branas.

Em 1997, Juan Maldacena observou que as excitações de baixa energia de uma teoria perto de um buraco negro consistem em objetos próximos do horizonte, o que para buracos negros com carga extrema parece um espaço anti-de Sitter. Ele observou que neste limite a teoria de calibre descreve as excitações das cordas próximas às branas. Então ele levantou a hipótese de que a teoria das cordas em uma geometria de buraco negro com carga extrema no horizonte próximo, um espaço anti-de Sitter vezes uma esfera com fluxo, é igualmente bem descrita pela teoria de calibre limitante de baixa energia, o N = 4 supersimétrico Yang –Teoria de Mills. Esta hipótese, que é chamada de correspondência AdS/CFT, foi desenvolvida por Steven Gubser, Igor Klebanov e Alexander Polyakov, e por Edward Witten, e é agora bem aceita. É uma realização concreta do princípio holográfico, que tem implicações de longo alcance para os buracos negros, a localidade e a informação na física, bem como para a natureza da interação gravitacional. Através desta relação, a teoria das cordas demonstrou estar relacionada com teorias de calibre como a cromodinâmica quântica e isto levou a uma compreensão mais quantitativa do comportamento dos hádrons, trazendo a teoria das cordas de volta às suas raízes.

Críticas

Número de soluções

Para construir modelos de física de partículas baseados na teoria das cordas, os físicos normalmente começam especificando uma forma para as dimensões extras do espaço-tempo. Cada uma dessas diferentes formas corresponde a um universo possível diferente, ou “estado de vácuo”, com uma coleção diferente de partículas e forças. A teoria das cordas, tal como é entendida atualmente, tem um enorme número de estados de vácuo, normalmente estimados em cerca de 10⁵⁰⁰, e estes podem ser suficientemente diversos para acomodar quase qualquer fenômeno que possa ser observado em baixas energias.

Muitos críticos da teoria das cordas expressaram preocupações sobre o grande número de universos possíveis descritos pela teoria das cordas. Em seu livro Not Even Wrong, Peter Woit, professor do departamento de matemática da Universidade de Columbia, argumentou que o grande número de diferentes cenários físicos torna a teoria das cordas vazia como estrutura para a construção de modelos de física de partículas.. De acordo com Woit,

A possível existência de, digamos, 10.^500. estados de vácuo diferentes consistentes para a teoria de superstring provavelmente destrói a esperança de usar a teoria para prever qualquer coisa. Se se escolher entre este grande conjunto apenas aqueles estados cujas propriedades concordam com observações experimentais presentes, é provável que ainda haverá um grande número destes que se pode obter praticamente qualquer valor que se quer para os resultados de qualquer nova observação.

Alguns físicos acreditam que este grande número de soluções é na verdade uma virtude porque pode permitir uma explicação antrópica natural dos valores observados das constantes físicas, em particular o pequeno valor da constante cosmológica. O princípio antrópico é a ideia de que alguns dos números que aparecem nas leis da física não são fixados por nenhum princípio fundamental, mas devem ser compatíveis com a evolução da vida inteligente. Em 1987, Steven Weinberg publicou um artigo no qual argumentava que a constante cosmológica não poderia ter sido muito grande, caso contrário as galáxias e a vida inteligente não teriam sido capazes de se desenvolver. Weinberg sugeriu que pode haver um grande número de universos consistentes possíveis, cada um com um valor diferente da constante cosmológica, e as observações indicam um pequeno valor da constante cosmológica apenas porque os humanos vivem em um universo que permitiu vida inteligente, e portanto, observadores, para existir.

O teórico das cordas Leonard Susskind argumentou que a teoria das cordas fornece uma explicação antrópica natural do pequeno valor da constante cosmológica. De acordo com Susskind, os diferentes estados de vácuo da teoria das cordas podem ser realizados como diferentes universos dentro de um multiverso maior. O fato de o universo observado ter uma constante cosmológica pequena é apenas uma consequência tautológica do fato de que é necessário um valor pequeno para a existência de vida. Muitos teóricos e críticos proeminentes discordaram das conclusões de Susskind. Segundo Woit, “neste caso [o raciocínio antrópico] nada mais é do que uma desculpa para o fracasso. As ideias científicas especulativas falham não apenas quando fazem previsões incorretas, mas também quando se revelam vazias e incapazes de prever qualquer coisa.

Compatibilidade com energia escura

Ainda não se sabe se a teoria das cordas é compatível com uma constante cosmológica positiva e metaestável. Existem alguns exemplos putativos de tais soluções, como o modelo descrito por Kachru et al. em 2003. Em 2018, um grupo de quatro físicos apresentou uma conjectura controversa que implicaria que tal universo não existe. Isto é contrário a alguns modelos populares de energia escura, como o Λ-CDM, que requer energia de vácuo positiva. No entanto, a teoria das cordas é provavelmente compatível com certos tipos de quintessência, onde a energia escura é causada por um novo campo com propriedades exóticas.

Independência de plano de fundo

Uma das propriedades fundamentais da teoria geral da relatividade de Einstein é que ela é independente do contexto, o que significa que a formulação da teoria não privilegia de forma alguma uma geometria do espaço-tempo específica.

Uma das principais críticas à teoria das cordas desde o início é que ela não é manifestamente independente de antecedentes. Na teoria das cordas, normalmente deve-se especificar uma geometria de referência fixa para o espaço-tempo, e todas as outras geometrias possíveis são descritas como perturbações desta geometria fixa. Em seu livro The Trouble With Physics, o físico Lee Smolin, do Perimeter Institute for Theoretical Physics, afirma que esta é a principal fraqueza da teoria das cordas como uma teoria da gravidade quântica, dizendo que a teoria das cordas não conseguiu incorporar esta importante visão da relatividade geral.

Outros discordaram da caracterização da teoria das cordas feita por Smolin. Em uma resenha do livro de Smolin, o teórico das cordas Joseph Polchinski escreve

[Smolin] está confundindo um aspecto da linguagem matemática que está sendo usada para uma da física que está sendo descrita. Novas teorias físicas são muitas vezes descobertas usando uma linguagem matemática que não é a mais adequada para eles... Na teoria das cordas, sempre foi claro que a física é independente de fundo mesmo que a linguagem que está sendo usada não seja, e a busca por uma linguagem mais adequada continua. De fato, como Smolin observa tardiamente, [AdS/CFT] fornece uma solução para este problema, que é inesperado e poderoso.

Polchinski observa que um importante problema em aberto na gravidade quântica é desenvolver descrições holográficas da gravidade que não exijam que o campo gravitacional seja assintoticamente anti-de Sitter. Smolin respondeu dizendo que a correspondência AdS/CFT, tal como é actualmente entendida, pode não ser suficientemente forte para resolver todas as preocupações sobre a independência de base.

Sociologia da ciência

Desde as revoluções das supercordas das décadas de 1980 e 1990, a teoria das cordas tem sido um dos paradigmas dominantes da física teórica de altas energias. Alguns teóricos das cordas expressaram a opinião de que não existe uma teoria alternativa igualmente bem-sucedida que aborde as questões profundas da física fundamental. Numa entrevista de 1987, o ganhador do Nobel David Gross fez os seguintes comentários controversos sobre as razões da popularidade da teoria das cordas:

O mais importante [razão] é que não há outras boas ideias ao redor. É isso que faz com que a maioria das pessoas se meta nisso. Quando as pessoas começaram a se interessar pela teoria das cordas, não sabiam nada disso. Na verdade, a primeira reação da maioria das pessoas é que a teoria é extremamente feia e desagradável, pelo menos esse foi o caso há alguns anos quando a compreensão da teoria das cordas foi muito menos desenvolvida. Era difícil para as pessoas aprenderem sobre isso e ser ligado. Então eu acho que a verdadeira razão pela qual as pessoas se atraíram por isso é porque não há outro jogo na cidade. Todas as outras abordagens da construção de grandes teorias unificadas, que foram mais conservadoras para começar, e só gradualmente se tornaram cada vez mais radicais, falharam, e este jogo ainda não falhou.

Vários outros teóricos e comentaristas de alto nível expressaram opiniões semelhantes, sugerindo que não existem alternativas viáveis à teoria das cordas.

Muitos críticos da teoria das cordas comentaram este estado de coisas. Em seu livro criticando a teoria das cordas, Peter Woit vê o status da pesquisa na teoria das cordas como prejudicial à saúde e prejudicial ao futuro da física fundamental. Ele argumenta que a extrema popularidade da teoria das cordas entre os físicos teóricos é em parte uma consequência da estrutura financeira da academia e da competição feroz por recursos escassos. Em seu livro The Road to Reality, o físico matemático Roger Penrose expressa opiniões semelhantes, afirmando que “A competitividade muitas vezes frenética que essa facilidade de comunicação gera leva a efeitos de movimento, onde os pesquisadores temem ser deixados para trás”. se eles não participarem." Penrose também afirma que a dificuldade técnica da física moderna obriga os jovens cientistas a confiar nas preferências de investigadores estabelecidos, em vez de abrirem novos caminhos próprios. Lee Smolin expressa uma posição ligeiramente diferente na sua crítica, alegando que a teoria das cordas cresceu a partir de uma tradição de física de partículas que desencoraja a especulação sobre os fundamentos da física, enquanto a sua abordagem preferida, a gravidade quântica em loop, encoraja um pensamento mais radical. De acordo com Smolin,

A teoria das cordas é uma ideia poderosa, bem motivada e merece grande parte do trabalho que lhe foi dedicado. Se até agora falhou, a principal razão é que suas falhas intrínsecas estão estreitamente ligadas a seus pontos fortes - e, claro, a história é inacabada, uma vez que a teoria das cordas pode bem resultar para ser parte da verdade. A verdadeira questão não é por isso que gastamos tanta energia na teoria das cordas, mas porque não gastamos quase o suficiente em abordagens alternativas.

Smolin continua oferecendo uma série de receitas sobre como os cientistas podem encorajar uma maior diversidade de abordagens para a pesquisa da gravidade quântica.