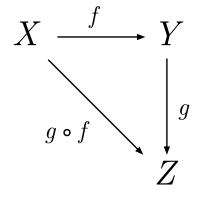Teoria da categoria

Representação esquemática de uma categoria com objetos X, Y, Z. e morfismos f, g, g ∘ f. (Os três morfismos de identidade da categoria 1_X1_Y e 1_Z., se explicitamente representado, apareceria como três flechas, das letras X, Y e Z para si, respectivamente.)

Teoria das categorias é uma teoria geral de estruturas matemáticas e suas relações que foi introduzida por Samuel Eilenberg e Saunders Mac Lane em meados do século 20 em seu trabalho fundamental sobre topologia algébrica. Atualmente, a teoria das categorias é usada em quase todas as áreas da matemática e em muitas áreas da ciência da computação. Em particular, numerosas construções de novos objetos matemáticos a partir de anteriores, que aparecem de forma semelhante em vários contextos, são convenientemente expressas e unificadas em termos de categorias. Os exemplos incluem espaços quocientes, produtos diretos, conclusão e dualidade.

Uma categoria é formada por dois tipos de objetos: os objetos da categoria e os morfismos, que relacionam dois objetos chamados de origem e destino do morfismo. Costuma-se dizer que um morfismo é uma seta que mapeia sua origem para seu destino. Os morfismos podem ser compostos se o alvo do primeiro morfismo for igual à fonte do segundo, e a composição do morfismo tem propriedades semelhantes à composição da função (associatividade e existência de morfismos de identidade). Os morfismos geralmente são algum tipo de função, mas nem sempre é o caso. Por exemplo, um monóide pode ser visto como uma categoria com um único objeto, cujos morfismos são os elementos do monóide.

O segundo conceito fundamental da teoria da categoria é o conceito de um funtor, que desempenha o papel de um morfismo entre duas categorias C1Não. C_{1}} e C2:Não. C_{2}: mapeia objetos de C1Não. C_{1}} a objetos de C2{displaystyle C_{2}} e morfismos de C1Não. C_{1}} aos morfismos de C2{displaystyle C_{2}} de tal forma que as fontes são mapeadas para fontes e alvos são mapeados para alvos (ou, no caso de um funtor contravariante, fontes são mapeadas para alvos e vice-versa). Um terceiro conceito fundamental é uma transformação natural que pode ser vista como um morfismo de funtores.

Categorias, objetos e morfismos

Categorias

Uma categoria C consiste nas seguintes três entidades matemáticas:

• Uma classe ob(C), cujos elementos são chamados objetos;
• A classe hom(C), cujos elementos são chamados morfismos ou mapas ou flechas.
  Cada morfismo f tem um objeto fonte um e objeto alvo b).
  A expressão f: um → b), seria verbalmente declarada como "f é um morfismo de um para b)".
  A expressão Olá.um, b)) – alternativamente expressa como Olá._C(um, b)), O quê?um, b))ou C(um, b)) – denota os hom-classe de todos os morfismos um para b).
• Uma operação binária,, chamada composição de morfismos, tal que
  para três objetos um, b)e cnós temos

:: hom(b), c)um, b)) → hom(um, c).

A composição de f: um → b) e g: b) → c é escrito como g ∘ f ou G., governado por dois axiomas:

1. Associatividade: Se f: um → b), g: b) → ce h: c → D então

h (em inglês)g ∘ f) = (h ∘ g) f

2. Identidade: Para cada objeto xexiste um morfismo 1_x: x → x chamado de morfismo de identidade para x,
tal que

para cada morfismo f: um → b)nós temos

1_b) ∘ f = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = f = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = f id_um.

Dos axiomas, pode-se provar que existe exatamente um morfismo de identidade para cada objeto.

Morfismos

Relações entre morfismos (como fg = h) geralmente são representadas usando diagramas comutativos, com "pontos" (cantos) representando objetos e "setas" representando morfismos.

Morfismos podem ter qualquer uma das seguintes propriedades. Um morfismo f: a → b é um:

• monomorfismo (ou Mês) se f ∘ g₁ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = f ∘ g₂ implica g₁ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = g₂ para todos os morfismos g₁, g₂: x → um.
• epimorfismo (ou Épico) se g₁ ∘ f = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = g₂ ∘ f implica g₁ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = g₂ para todos os morfismos g₁, g₂: b) → x.
• bimorfismo se f é épico e moníaco.
• isomorfismo se existe um morfismo g: b) → um tal que f ∘ g = 1_b) e g ∘ f = 1_um.
• endomorfismo se um = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = b). end(um) denota a classe de endomorfismos de um.
• automorfismo se f é um endomorfismo e um isomorfismo. Aut(um) denota a classe de automorfismos de um.
• retração se um inverso direito de f existe, ou seja, se existe um morfismo g: b) → um com f ∘ g = 1_b).
• seção se um inverso esquerdo de f existe, ou seja, se existe um morfismo g: b) → um com g ∘ f = 1_um.

Toda retração é um epimorfismo e toda seção é um monomorfismo. Além disso, as três declarações a seguir são equivalentes:

• f é um monomorfismo e uma retração;
• f é um epimorfismo e uma seção;
• f é um isomorfismo.

Funtores

Functores são mapas de preservação de estrutura entre categorias. Eles podem ser pensados como morfismos na categoria de todas as (pequenas) categorias.

Um (covariante) functor F de uma categoria C para uma categoria D, escrito F: C → D, consiste em:

• para cada objeto x em C, um objeto F(x) em D; e
• para cada morfismo f: x → Sim. em C, um morfismo F(f): F(x) → F(Sim.) em D,

de modo que as duas propriedades a seguir sejam válidas:

• Para cada objeto x em C, F(1_x) = 1_F(x);
• Para todos os morfismos f: x → Sim. e g: Sim. → zangão., F(g ∘ f) = F(g) F(f).

Um funtor contravariante F: C → D é como um functor covariante, exceto que "inverte os morfismos" ("inverte todas as setas"). Mais especificamente, cada morfismo f: x → y em C deve ser atribuído a um morfismo F(f): F(y) → F(x) em D. Em outras palavras, um functor contravariante atua como um functor covariante da categoria oposta C^op a D.

Transformações naturais

Uma transformação natural é uma relação entre dois functores. Functors frequentemente descrevem "construções naturais" e transformações naturais então descrevem "homomorfismos naturais" entre duas dessas construções. Às vezes, duas construções bastante diferentes produzem "o mesmo" resultado; isto é expresso por um isomorfismo natural entre os dois functores.

Se F e G são funtores (covariantes) entre as categorias C e D, então um natural a transformação η de F para G associa a cada objeto X em C um morfismo η_X: F(X) → G(X ) em D tal que para cada morfismo f: X → Y em C, temos η_Y ∘ F(f) = G(f) ∘ η_X; isso significa que o seguinte diagrama é comutativo:

Os dois funtores F e G são chamados naturalmente isomórficos se existe uma transformação natural de F para G tal que η_X é um isomorfismo para todo objeto X em C.

Outros conceitos

Construções universais, limites e colimites

Usando a linguagem da teoria das categorias, muitas áreas de estudo matemático podem ser categorizadas. As categorias incluem conjuntos, grupos e topologias.

Cada categoria se distingue por propriedades que todos os seus objetos têm em comum, como o conjunto vazio ou o produto de duas topologias, porém na definição de uma categoria, os objetos são considerados atômicos, ou seja, não saber se um objeto A é um conjunto, uma topologia ou qualquer outro conceito abstrato. Assim, o desafio é definir objetos especiais sem se referir à estrutura interna desses objetos. Para definir o conjunto vazio sem fazer referência aos elementos, ou a topologia do produto sem fazer referência aos conjuntos abertos, pode-se caracterizar esses objetos em termos de suas relações com outros objetos, conforme dados pelos morfismos das respectivas categorias. Assim, a tarefa é encontrar propriedades universais que determinem exclusivamente os objetos de interesse.

Numerosas construções importantes podem ser descritas de forma puramente categórica se o limite de categoria puder ser desenvolvido e dualizado para produzir a noção de um colimite.

Categorias equivalentes

É uma pergunta natural a se fazer: sob quais condições duas categorias podem ser consideradas essencialmente iguais, no sentido de que teoremas sobre uma categoria podem ser facilmente transformados em teoremas sobre a outra categoria? A principal ferramenta que se emprega para descrever tal situação é chamada equivalência de categorias, que é dada por functores apropriados entre duas categorias. A equivalência categórica encontrou inúmeras aplicações em matemática.

Mais conceitos e resultados

As definições de categorias e functores fornecem apenas o básico da álgebra categórica; tópicos adicionais importantes estão listados abaixo. Embora existam fortes inter-relações entre todos esses tópicos, a ordem dada pode ser considerada como uma diretriz para leitura posterior.

• A categoria do funtor D^C tem como objetos os funtores de C para D e como morfismos as transformações naturais de tais funtores. O lemma de Yoneda é um dos resultados básicos mais famosos da teoria da categoria; ele descreve funtores representáveis em categorias de funtores.
• Dualidade: Cada declaração, teorema ou definição na teoria da categoria tem uma dual que é essencialmente obtido por "reversão de todas as flechas". Se uma declaração é verdadeira em uma categoria C então sua dupla é verdadeira na categoria dupla C^O. Esta dualidade, que é transparente no nível da teoria da categoria, é muitas vezes obscurecida em aplicações e pode levar a relações surpreendentes.
• Funtores adjacentes: Um funtor pode ser deixado (ou direito) junto a outro funtor que mapeia na direção oposta. Tal par de funtores adjuntos tipicamente surge de uma construção definida por uma propriedade universal; isso pode ser visto como uma visão mais abstrata e poderosa sobre propriedades universais.

Categorias de dimensão superior

Muitos dos conceitos acima, especialmente equivalência de categorias, pares de funtores adjuntos e categorias de funtores, podem ser situados no contexto de categorias de dimensão superior. Resumidamente, se considerarmos um morfismo entre dois objetos como um "processo que nos leva de um objeto para outro", então as categorias de dimensão superior nos permitem generalizar isso de maneira lucrativa, considerando os "processos de dimensão superior" 34;.

Por exemplo, uma 2-categoria (estrita) é uma categoria junto com "morfismos entre morfismos", ou seja, processos que nos permitem transformar um morfismo em outro. Podemos então "compor" esses "bimorfismos" horizontal e verticalmente, e exigimos uma "lei de troca" manter, relacionando as duas leis de composição. Neste contexto, o exemplo padrão é Cat, a 2-categoria de todas as (pequenas) categorias e, neste exemplo, bimorfismos de morfismos são simplesmente transformações naturais de morfismos no sentido usual. Outro exemplo básico é considerar uma categoria 2 com um único objeto; estas são essencialmente categorias monoidais. Bicategorias são uma noção mais fraca de categorias bidimensionais em que a composição de morfismos não é estritamente associativa, mas apenas associativa "até" um isomorfismo.

Este processo pode ser estendido para todos os números naturais n, e estes são chamados de n-categorias. Existe até uma noção de ω-categoria correspondente ao número ordinal ω.

As categorias de dimensão superior fazem parte do campo matemático mais amplo da álgebra de dimensão superior, um conceito introduzido por Ronald Brown. Para uma introdução conversacional a essas ideias, consulte John Baez, 'A Tale of n-categories' (1996).

Notas históricas

Deve-se observar primeiro que todo o conceito de uma categoria é essencialmente auxiliar; nossos conceitos básicos são essencialmente aqueles de um funtor e de uma transformação natural [...]

—Eilenberg e Mac Lane (1945)

Embora exemplos específicos de functores e transformações naturais tenham sido dados por Samuel Eilenberg e Saunders Mac Lane em um artigo de 1942 sobre teoria de grupos, esses conceitos foram introduzidos em um sentido mais geral, juntamente com a noção adicional de categorias, em um artigo de 1945 artigo dos mesmos autores (que discutiram as aplicações da teoria das categorias ao campo da topologia algébrica). Seu trabalho foi uma parte importante da transição da homologia intuitiva e geométrica para a álgebra homológica, Eilenberg e Mac Lane escreveram mais tarde que seu objetivo era entender as transformações naturais, que primeiro exigiam a definição de functores, depois categorias.

Stanislaw Ulam, e alguns escritos em seu nome, afirmaram que ideias relacionadas eram correntes no final da década de 1930 na Polônia. Eilenberg era polonês e estudou matemática na Polônia na década de 1930. A teoria das categorias também é, em certo sentido, uma continuação do trabalho de Emmy Noether (uma das professoras de Mac Lane) na formalização de processos abstratos; Noether percebeu que entender um tipo de estrutura matemática requer entender os processos que preservam essa estrutura (homomorfismos). Eilenberg e Mac Lane introduziram categorias para entender e formalizar os processos (functores) que relacionam estruturas topológicas com estruturas algébricas (invariantes topológicos) que as caracterizam.

A teoria das categorias foi originalmente introduzida para a necessidade da álgebra homológica e amplamente estendida para a necessidade da geometria algébrica moderna (teoria do esquema). A teoria das categorias pode ser vista como uma extensão da álgebra universal, já que a última estuda estruturas algébricas, e a primeira se aplica a qualquer tipo de estrutura matemática e estuda também as relações entre estruturas de diferentes naturezas. Por esse motivo, é usado em toda a matemática. Aplicações à lógica matemática e semântica (máquina abstrata categórica) vieram depois.

Certas categorias chamadas topoi (singulares topos) podem até servir como uma alternativa à teoria axiomática dos conjuntos como fundamento da matemática. Um topos também pode ser considerado como um tipo específico de categoria com dois axiomas topos adicionais. Essas aplicações fundamentais da teoria das categorias foram elaboradas com bastante detalhe como base e justificativa para a matemática construtiva. A teoria dos topos é uma forma de teoria abstrata do feixe, com origens geométricas, e leva a ideias como a topologia sem sentido.

A lógica categórica é agora um campo bem definido baseado na teoria de tipos para lógicas intuicionistas, com aplicações em programação funcional e teoria de domínio, onde uma categoria fechada cartesiana é tomada como uma descrição não sintática de um cálculo lambda. No mínimo, a linguagem teórica da categoria esclarece o que exatamente essas áreas relacionadas têm em comum (em algum sentido abstrato).

A teoria da categoria também foi aplicada em outros campos. Por exemplo, John Baez mostrou uma ligação entre os diagramas de Feynman na física e as categorias monoidais. Outra aplicação da teoria das categorias, mais especificamente: a teoria dos topos, foi feita na teoria matemática da música, veja por exemplo o livro Os Topos da Música, Lógica Geométrica dos Conceitos, Teoria e Performance de Guerino Mazzola.

Esforços mais recentes para apresentar categorias aos alunos de graduação como base para a matemática incluem os de William Lawvere e Rosebrugh (2003) e Lawvere e Stephen Schanuel (1997) e Mirroslav Yotov (2012).