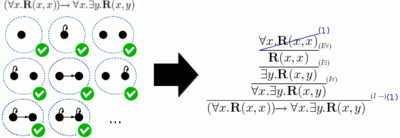
Teorema da completude de Gödel

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Teorema fundamental na lógica matemática

A fórmula (∀)x. R(x,x) →xDetalheSim.. R(x,Sim.)) detém em todas as estruturas (apenas os 8 mais simples são mostrados à esquerda). Pelo resultado da plenitude de Gödel, deve, portanto, ter uma prova natural de dedução (direita mostrada).

Teorema da completude de Gödel é um teorema fundamental na lógica matemática que estabelece uma correspondência entre a verdade semântica e a demonstrabilidade sintática na lógica de primeira ordem.

O teorema da completude se aplica a qualquer teoria de primeira ordem: se T é tal teoria e φ é uma sentença (no mesmo idioma) e todo modelo de T é um modelo de φ, então há uma prova (de primeira ordem) de φ usando as declarações de T como axiomas. Às vezes se diz isso como "qualquer coisa universalmente verdadeira é demonstrável". Isso não contradiz o teorema da incompletude de Gödel, que mostra que alguma fórmula φ_u é improvável, embora verdadeira nos números naturais, que são um modelo particular de uma teoria de primeira ordem que os descreve - φ _u é apenas falso em algum outro modelo da teoria de primeira ordem sendo considerada (como um modelo não padrão de aritmética para a aritmética de Peano). Esse tipo de falha de consistência entre um modelo padrão e não padrão também é chamado de Inconsistência Ômega.

Ele faz uma estreita ligação entre a teoria do modelo que lida com o que é verdadeiro em diferentes modelos e a teoria da prova que estuda o que pode ser formalmente provado em sistemas formais particulares.

Foi provado pela primeira vez por Kurt Gödel em 1929. Foi então simplificado quando Leon Henkin observou em seu Ph.D. tese de que a parte difícil da prova pode ser apresentada como o Teorema da Existência do Modelo (publicado em 1949). A prova de Henkin foi simplificada por Gisbert Hasenjaeger em 1953.

Preliminares

Existem numerosos sistemas dedutivos para lógica de primeira ordem, incluindo sistemas de dedução natural e sistemas de estilo Hilbert. Comum a todos os sistemas dedutivos é a noção de uma dedução formal. Esta é uma sequência (ou, em alguns casos, uma árvore finita) de fórmulas com uma conclusão especialmente designada. A definição de uma dedução é tal que é finita e que é possível verificar algoritmicamente (por um computador, por exemplo, ou à mão) que uma determinada sequência (ou árvore) de fórmulas é de fato uma dedução.

Uma fórmula de primeira ordem é chamada logicamente válida se for verdadeira em todas as estruturas para a linguagem da fórmula (ou seja, para qualquer atribuição de valores às variáveis da fórmula). Para declarar formalmente e depois provar o teorema da completude, é necessário também definir um sistema dedutivo. Um sistema dedutivo é chamado completo se toda fórmula logicamente válida é a conclusão de alguma dedução formal, e o teorema da completude para um sistema dedutivo particular é o teorema de que ele é completo nesse sentido. Assim, em certo sentido, existe um teorema de completude diferente para cada sistema dedutivo. Um inverso à completude é a solidez, o fato de que apenas fórmulas logicamente válidas são demonstráveis no sistema dedutivo.

Se algum sistema dedutivo específico de lógica de primeira ordem é sólido e completo, então ele é "perfeito" (uma fórmula é demonstrável se e somente se for logicamente válida), portanto equivalente a qualquer outro sistema dedutivo com a mesma qualidade (qualquer prova em um sistema pode ser convertida em outro).

Declaração

Primeiro fixamos um sistema dedutivo de cálculo de predicados de primeira ordem, escolhendo qualquer um dos sistemas equivalentes conhecidos. A prova original de Gödel assumiu o sistema de prova de Hilbert-Ackermann.

Formulação original de Gödel

O teorema da completude diz que se uma fórmula é logicamente válida, então há uma dedução finita (uma prova formal) da fórmula.

Assim, o sistema dedutivo é "completo" no sentido de que nenhuma regra de inferência adicional é necessária para provar todas as fórmulas logicamente válidas. Um inverso à completude é a solidez, o fato de que apenas fórmulas logicamente válidas são demonstráveis no sistema dedutivo. Juntamente com a solidez (cuja verificação é fácil), esse teorema implica que uma fórmula é logicamente válida se e somente se for a conclusão de uma dedução formal.

Forma mais geral

O teorema pode ser expresso mais geralmente em termos de consequência lógica. Nós dizemos que uma sentença S é um consequência sintática de uma teoria T, denotado ${displaystyle Tvdash s}$ , se S é provável de T em nosso sistema dedutivo. Nós dizemos que S é um consequência semântica de T, denotado ${displaystyle Tmodels s}$ , se S em cada modelo de T. O teorema da plenitude, em seguida, diz que para qualquer teoria da primeira ordem T com uma linguagem bem ordenada, e qualquer frase S na língua de T,

{displaystyle Tmodels s}

, então

{displaystyle Tvdash s}

Uma vez que o inverso (sonho) também detém, segue-se que ${displaystyle Tmodels s}$ se e somente se ${displaystyle Tvdash s}$ , e assim que a consequência sintática e semântica são equivalentes para a lógica de primeira ordem.

Esse teorema mais geral é usado implicitamente, por exemplo, quando se mostra que uma sentença é demonstrável a partir dos axiomas da teoria de grupos considerando um grupo arbitrário e mostrando que a sentença é satisfeita por aquele grupo.

A formulação original de Gödel é deduzida tomando o caso particular de uma teoria sem nenhum axioma.

Teorema de existência do modelo

O teorema da completude também pode ser entendido em termos de consistência, como consequência do teorema de existência do modelo de Henkin. Dizemos que uma teoria T é sintaticamente consistente se não existe uma sentença s tal que tanto s quanto sua negação ¬s são demonstráveis a partir de T em nosso sistema dedutivo. O teorema da existência do modelo diz que para qualquer teoria de primeira ordem T com uma linguagem bem ordenável,

T

é sinteticamente consistente, então

T

tem um modelo.

Outra versão, com conexões com o teorema de Löwenheim–Skolem, diz:

Cada teoria sinteticamente consistente e contável de primeira ordem tem um modelo finito ou contável.

Dado o teorema de Henkin, o teorema da plenitude pode ser provado como segue: Se ${displaystyle Tmodels s}$ , então ${displaystyle Tcup lnot s}$ não tem modelos. Pelo contrapositivo do teorema de Henkin, então ${displaystyle Tcup lnot s}$ é sinteticamente inconsistente. Então uma contradição ( $bot$ ) é provável de ${displaystyle Tcup lnot s}$ no sistema dedutivo. Daí ${displaystyle (Tcup lnot s)vdash bot }$ , e então pelas propriedades do sistema dedutivo, ${displaystyle Tvdash s}$ .

Como um teorema de aritmética

O teorema de existência do modelo e sua prova podem ser formalizados na estrutura da aritmética de Peano. Precisamente, podemos definir sistematicamente um modelo de qualquer teoria efetiva consistente de primeira ordem T na aritmética de Peano interpretando cada símbolo de T por uma fórmula aritmética cujas variáveis livres são os argumentos do símbolo. (Em muitos casos, precisaremos assumir, como hipótese da construção, que T é consistente, pois a aritmética de Peano pode não provar esse fato.) No entanto, a definição expressa por essa fórmula não é recursivo (mas é, em geral, Δ2).

Consequências

Uma consequência importante do teorema da completude é que é possível enumerar recursivamente as consequências semânticas de qualquer teoria de primeira ordem eficaz, enumerando todas as possíveis deduções formais dos axiomas da teoria e usar isso para produzir uma enumeração das suas conclusões.

Isso contrasta com o significado direto da noção de consequência semântica, que quantifica sobre todas as estruturas em uma linguagem particular, que claramente não é uma definição recursiva.

Além disso, torna o conceito de "provabilidade", e portanto de "teorema", um conceito claro que depende apenas do sistema de axiomas da teoria escolhido, e não de a escolha de um sistema de prova.

Relação com os teoremas da incompletude

Os teoremas da incompletude de Gödel mostram que existem limitações inerentes ao que pode ser provado dentro de qualquer teoria de primeira ordem dada em matemática. A "incompletude" em seu nome refere-se a outro significado de completo (veja a teoria do modelo – Usando os teoremas de compactação e integridade): Uma teoria $T$ é completo (ou decidível) se cada frase $S$ na língua de $T$ ou é provável ( ${displaystyle Tvdash S}$ ) ou reprovável ( ${displaystyle Tvdash neg S}$ ).

O primeiro teorema da incompletude afirma que qualquer $T$ que é consistente, eficaz e contém Robinson aritmética ("Q") deve ser incompleto nesse sentido, construindo explicitamente uma frase ${displaystyle S_{T}}$ que não é demonstrável nem desprovível dentro $T$ . O segundo teorema da incompletude estende este resultado, mostrando que ${displaystyle S_{T}}$ pode ser escolhido para que expresse a consistência de $T$ em si.

Desde então ${displaystyle S_{T}}$ não pode ser provado $T$ , o teorema da plenitude implica a existência de um modelo de $T$ em que ${displaystyle S_{T}}$ é falso. Na verdade, ${displaystyle S_{T}}$ é uma frase Π1, ou seja, afirma que alguma propriedade finita é verdadeira de todos os números naturais; então, se é falsa, então algum número natural é um contra-exemplo. Se este contra-exemplo existisse dentro dos números naturais padrão, sua existência iria refutar ${displaystyle S_{T}}$ dentro de $T$ ; mas o teorema da incompletude mostrou que isto era impossível, então o contra-exemplo não deve ser um número padrão, e assim qualquer modelo de $T$ em que ${displaystyle S_{T}}$ é falso deve incluir números não-padrão.

Na verdade, o modelo de qualquer teoria contendo Q obtido pela construção sistemática do teorema de existência do modelo aritmético, é sempre não padrão com um predicado de demonstrabilidade não equivalente e uma maneira não equivalente de interpretar sua própria construção, de modo que essa construção não seja recursiva (já que as definições recursivas seriam inequívocas).

Também, se $T$ é pelo menos ligeiramente mais forte do que Q (por exemplo, se inclui indução para fórmulas existenciais limitadas), então o teorema de Tennenbaum mostra que não tem modelos recursivos não padronizados.

Relação com o teorema da compacidade

O teorema da completude e o teorema da compacidade são dois pilares da lógica de primeira ordem. Embora nenhum desses teoremas possa ser comprovado de maneira completamente eficaz, cada um pode ser efetivamente obtido do outro.

O teorema da compacidade diz que se uma fórmula φ é uma consequência lógica de um conjunto (possivelmente infinito) de fórmulas Γ, então é uma consequência lógica de um subconjunto finito de Γ. Esta é uma consequência imediata do teorema da completude, porque apenas um número finito de axiomas de Γ pode ser mencionado em uma dedução formal de φ, e a solidez do sistema dedutivo implica então que φ é uma consequência lógica deste conjunto finito. Esta prova do teorema da compacidade é originalmente devida a Gödel.

Por outro lado, para muitos sistemas dedutivos, é possível provar o teorema da completude como uma consequência efetiva do teorema da compacidade.

A ineficácia do teorema da completude pode ser medida de acordo com as linhas da matemática reversa. Quando considerados sobre uma linguagem contável, os teoremas da completude e da compacidade são equivalentes entre si e equivalentes a uma forma fraca de escolha conhecida como lema fraco de König, com a equivalência demonstrável em RCA₀ (uma variante de segunda ordem da aritmética de Peano restrita à indução sobre Σ⁰₁ fórmulas). O lema fraco de König é demonstrável em ZF, o sistema da teoria dos conjuntos de Zermelo-Fraenkel sem axioma de escolha e, portanto, os teoremas de completude e compacidade para linguagens contáveis são demonstráveis em ZF. No entanto, a situação é diferente quando a linguagem é de grande cardinalidade arbitrária desde então, embora os teoremas de completude e compacidade permaneçam comprovadamente equivalentes um ao outro em ZF, eles também são comprovadamente equivalentes a uma forma fraca do axioma de escolha conhecido como lema do ultrafiltro. Em particular, nenhuma teoria que estende ZF pode provar os teoremas de completude ou compacidade sobre linguagens arbitrárias (possivelmente incontáveis) sem também provar o lema do ultrafiltro em um conjunto de mesma cardinalidade.

Integridade em outras lógicas

O teorema da completude é uma propriedade central da lógica de primeira ordem que não se aplica a todas as lógicas. A lógica de segunda ordem, por exemplo, não possui um teorema de completude para sua semântica padrão (mas possui a propriedade de completude para a semântica de Henkin), e o conjunto de fórmulas logicamente válidas na lógica de segunda ordem não é recursivamente enumerável. O mesmo é verdade para todas as lógicas de ordem superior. É possível produzir sistemas dedutivos sólidos para lógicas de ordem superior, mas nenhum sistema desse tipo pode ser completo.

O teorema de Lindström afirma que a lógica de primeira ordem é a lógica mais forte (sujeita a certas restrições) satisfazendo tanto a compacidade quanto a completude.

Um teorema de completude pode ser provado para lógica modal ou lógica intuicionista em relação à semântica de Kripke.

Provas

A prova original do teorema de Gödel procedeu reduzindo o problema a um caso especial para fórmulas em uma certa forma sintática e, em seguida, manipulando essa forma com um argumento ad hoc.

Nos textos de lógica modernos, o teorema da completude de Gödel geralmente é provado com a prova de Henkin, em vez da prova original de Gödel. A prova de Henkin constrói diretamente um modelo de termo para qualquer teoria consistente de primeira ordem. James Margetson (2004) desenvolveu uma prova formal computadorizada usando o provador do teorema de Isabelle. Outras provas também são conhecidas.

Contenido relacionado

Más resultados...