Temperamento igual
Um temperamento igual é um temperamento musical ou sistema de afinação que aproxima apenas intervalos dividindo uma oitava (ou outro intervalo) em passos iguais. Isso significa que a proporção das frequências de qualquer par adjacente de notas é a mesma, o que dá um tamanho de passo percebido igual, pois o tom é percebido aproximadamente como o logaritmo da frequência.
Na música clássica e na música ocidental em geral, o sistema de afinação mais comum desde o século 18 é o temperamento igual a 12 tons (também conhecido como temperamento igual a 12, 12-TET ou 12-ET, informalmente abreviado como 12 iguais), que divide a oitava em 12 partes, todas iguais em uma escala logarítmica, com uma razão igual à raiz 12 de 2 (12 √2 ≈ 1.05946). O menor intervalo resultante, 1⁄12 o largura de uma oitava, é chamado de semitom ou meio tom. Nos países ocidentais, o termo temperamento igual, sem qualificação, geralmente significa 12-TET.
Nos tempos modernos, 12-TET é geralmente afinado em relação a um tom padrão de 440 Hz, chamado A440, o que significa que uma nota, A, é afinada em 440 hertz e todas as outras notas são definidas como alguns múltiplos de semitons distantes dela, seja maior ou menor em frequência. A afinação padrão nem sempre foi de 440 Hz; tem variado consideravelmente e geralmente aumentado ao longo dos últimos cem anos.
Outros temperamentos iguais dividem a oitava de maneira diferente. Por exemplo, algumas músicas foram escritas em 19-TET e 31-TET, enquanto o sistema de tom árabe usa 24-TET.
Em vez de dividir uma oitava, um temperamento igual também pode dividir um intervalo diferente, como a versão igualitária da escala de Bohlen-Pierce, que divide o intervalo justo de uma oitava e uma quinta (proporção 3:1), chamado de "tritave" ou uma "pseudo-oitava" nesse sistema, em 13 partes iguais.
Para sistemas de afinação que dividem a oitava igualmente, mas não são aproximações de apenas intervalos, o termo divisão igual da oitava ou EDO pode ser usado.
Conjuntos de cordas sem trastes, que podem ajustar a afinação de todas as notas, exceto para cordas abertas, e grupos vocais, que não têm limitações de afinação mecânica, às vezes usam uma afinação muito mais próxima da entonação por razões acústicas. Outros instrumentos, como alguns instrumentos de sopro, teclado e trastes, geralmente se aproximam apenas do temperamento igual, onde as limitações técnicas impedem afinações exatas. Alguns instrumentos de sopro que podem facilmente e espontaneamente dobrar seu tom, principalmente os trombones, usam afinação semelhante a conjuntos de cordas e grupos vocais.
Propriedades gerais
Em um temperamento igual, a distância entre dois passos adjacentes da escala é o mesmo intervalo. Como a identidade percebida de um intervalo depende de sua proporção, essa escala em etapas pares é uma sequência geométrica de multiplicações. (Uma sequência aritmética de intervalos não soaria uniformemente espaçada e não permitiria a transposição para tonalidades diferentes.) Especificamente, o menor intervalo em uma escala de temperamento igual é a razão:
- Rn= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =p- Sim.
- R= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =pnNão. r={sqrt[n]{p}}}
onde a proporção r divide a proporção p (normalmente a oitava, que é 2:1) em n partes iguais. (Consulte temperamento igual dodecafônico abaixo.)
As escalas geralmente são medidas em centavos, que dividem a oitava em 1.200 intervalos iguais (cada um chamado de centavo). Essa escala logarítmica torna a comparação de diferentes sistemas de afinação mais fácil do que a comparação de proporções e tem uso considerável em etnomusicologia. O passo básico em centavos para qualquer temperamento igual pode ser encontrado tomando a largura de p acima em centavos (geralmente a oitava, que tem 1200 centavos de largura), chamada abaixo de w, e dividindo-o em n partes:
- c= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =O quê?nNão. Não.
Na análise musical, o material pertencente a um temperamento igual geralmente recebe uma notação inteira, o que significa que um único inteiro é usado para representar cada altura. Isso simplifica e generaliza a discussão do material do tom dentro do temperamento da mesma forma que tomar o logaritmo de uma multiplicação o reduz à adição. Além disso, aplicando a aritmética modular onde o módulo é o número de divisões da oitava (geralmente 12), esses inteiros podem ser reduzidos a classes de notas, o que remove a distinção (ou reconhece a semelhança) entre notas de mesmo nome, por exemplo, c é 0 independentemente do registro de oitava. O padrão de codificação MIDI usa designações de notas inteiras.
Fórmulas gerais para o intervalo equilibrado
Temperamento igual dodecafônico
O temperamento igual de 12 tons, que divide a oitava em 12 intervalos de tamanho igual, é o sistema musical mais utilizado hoje, especialmente na música ocidental.
História
As duas figuras frequentemente creditadas com a obtenção do cálculo exato de temperamento igual são Zhu Zaiyu (também romanizado como Chu-Tsaiyu. Chinês: 朱 載堉) em 1584 e Simon Stevin em 1585. Segundo Fritz A. Kuttner, um crítico da teoria, sabe-se que Zhu "apresentou um método altamente preciso, simples e engenhoso para cálculo aritmético de mono-acordes de temperamento igual em 1584" e que Stevin "ofereceu uma definição matemática de temperamento igual mais um cálculo um pouco menos preciso dos valores numéricos correspondentes em 1585 ou mais tarde" Os desenvolvimentos ocorreram de forma independente.
Kenneth Robinson atribui a invenção do temperamento igual a Zhu e fornece citações textuais como evidência. Em um texto datado de 1584, Zhu escreveu: “Eu fundei um novo sistema. Estabeleço um pé como o número do qual os outros devem ser extraídos e, usando proporções, os extraio. Ao todo, é preciso encontrar os números exatos para os gaiteiros em doze operações." Kuttner discorda e observa que sua afirmação "não pode ser considerada correta sem maiores qualificações". Kuttner propõe que nem Zhu nem Stevin alcançaram temperamento igual e que nenhum deles deveria ser considerado um inventor.
China
A China já havia apresentado aproximações para 12-TET, mas Zhu foi a primeira pessoa a resolver matematicamente o temperamento igual de 12 tons, que ele descreveu em seu Fusão de Música e Calendário (律暦融通) em 1580 e Compêndio Completo de Música e Tom (Yuelü quan shu 樂律全書) em 1584. Joseph Needham também faz um relato extenso. Zhu obteve seu resultado dividindo o comprimento da corda e do tubo sucessivamente por 12√ 2 ≈ 1.059463, e para o comprimento do tubo em 24√2, de modo que após 12 divisões (uma oitava), o comprimento foi reduzido pela metade.
Zhu criou vários instrumentos afinados ao seu sistema, incluindo flautas de bambu.
Europa
Alguns dos primeiros europeus a defender o temperamento igual foram os alaudistas Vincenzo Galilei, Giacomo Gorzanis e Francesco Spinacino, todos os quais escreveram música nele.
Simon Stevin foi o primeiro a desenvolver o 12-TET baseado na décima segunda raiz de dois, que ele descreveu em Van De Spiegheling der singconst (ca. 1605), publicado postumamente em 1884.
Tocadores de instrumentos dedilhados (alaudistas e violonistas) geralmente favoreciam o temperamento igual, enquanto outros eram mais divididos. No final, o temperamento igual de 12 tons venceu. Isso permitiu que a modulação enarmônica, novos estilos de tonalidade simétrica e politonalidade, música atonal como aquela escrita com a técnica de 12 tons ou serialismo e jazz (pelo menos seu componente de piano) se desenvolvessem e florescessem.
Matemática
No temperamento igual de 12 tons, que divide a oitava em 12 partes iguais, a largura de um semitom, ou seja, a relação de frequência do intervalo entre duas notas adjacentes, é a décima segunda raiz de dois:
- 212= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2112? ? 1.05946[{12}]{2}}=2^{frac {1}{12}}approx 1.059463}
Este intervalo é dividido em 100 centavos.
Calculando frequências absolutas
Para encontrar a frequência, Pn, de uma nota em 12-TET, a seguinte definição pode ser usada:
- Pn= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Pum(212)(n- Sim. - Sim. um)Não. P_{n}=P_{a}left({sqrt[{12}]{2}}right)^{(n-a)}}
Nesta fórmula, Pn é o tom ou a frequência (geralmente em hertz) que você está tentando encontrar. Pa é a frequência de uma afinação de referência. n e a são números atribuídos à afinação desejada e à afinação de referência, respectivamente. Esses dois números são de uma lista de inteiros consecutivos atribuídos a semitons consecutivos. Por exemplo, A4 (a afinação de referência) é a 49ª tecla da extremidade esquerda de um piano (afinada em 440 Hz) e C4 (dó central), e F#4 são as 40ª e 46ª teclas, respectivamente. Esses números podem ser usados para encontrar a frequência de C4 e F#4:
- P40= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =440(212)(40- Sim. - Sim. 49)? ? 26.6.26H. H. H.zangão.Não. P_{40}=440left({sqrt[{12}]{2}}right)^{(40-49)}approx 261.626 mathrm {Hz} }
- P46.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =440(212)(46.- Sim. - Sim. 49)? ? 369.994H. H. H.zangão.Não. P_{46}=440left({sqrt[{12}]{2}}right)^{(46-49)}approx 369.994 mathrm {Hz} }
Convertendo frequências para suas contrapartes de temperamento igual
Para converter uma frequência (em Hz) em sua contraparte igual de 12 TET, a seguinte fórmula pode ser usada:
En= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =um)) 2rodada (12log2 (num))12Não. E_{n}=acdot 2^{frac {operatorname {round} left(12log _{2}left({frac {n}{a}}right)right)}{12}}}
En é a frequência de uma nota em temperamento igual, e a é a frequência de uma nota de referência. Por exemplo, se deixarmos a afinação de referência igual a 440 Hz, podemos ver que E5 e C#5 têm as seguintes frequências, respectivamente:
E660= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =440)) 2rodada (12log2 (660440))12? ? 659.255H. H. H.zangão.Não. E_{660}=440cdot 2^{frac {operatorname {round} left(12log _{2}left({frac {660}{440}}right)}{12}}approx 659.255\mathrm {Hz} }
E550= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =440)) 2rodada (12log2 (550440))12? ? 554.365H. H. H.zangão.Não. E_{550}=440cdot 2^{frac {operatorname {round} left(12log _{2}left({frac {550}{440}}right)}{12}}approx 554.365\mathrm {Hz} }
Comparação apenas com entonação
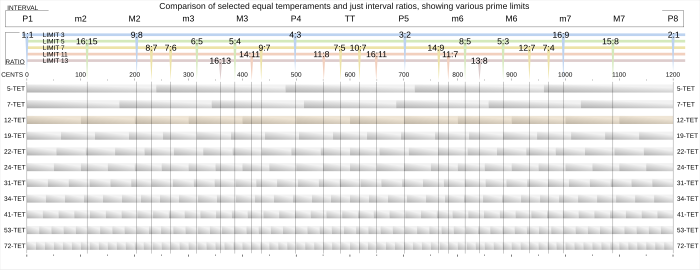
Os intervalos de 12-TET se aproximam de alguns intervalos apenas na entonação. As quintas e quartas estão quase indistinguivelmente próximas de apenas intervalos, enquanto as terças e sextas estão mais distantes.
Na tabela a seguir, os tamanhos de vários intervalos justos são comparados com suas contrapartes de temperamento igual, dados como uma proporção e também como centavos.
| Nome de Intervalação | Valor exato em 12-TET | Valor decimal em 12-TET | Cents | Apenas intervalo de entonação | Cents em apenas entonação | Variação |
|---|---|---|---|---|---|---|
| Unison (C) | 20?12 = 1 | 1 | 0 | 1?1 = 1 | 0 | 0 |
| Menor segundo (D♭) | 21?12 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 12√2 | 1.05946 | 100. | 16.?15 = 1.06666... | 111.73 | -11.73 |
| Segunda maior (D) | 22?12 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 6√2 | 1.122462 | 200 | 9?8 = 1.125 | 203.91 | -3.91 |
| Terceiro menor (E♭) | 23?12 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 4√2 | 1.18907 | 300 | 6?5 = 1.2 | 315.64 | -15.64 |
| Terceiro maior (E) | 24?12 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 3√2 | 1.2599 | 400 | 5?4 = 1.25 | 386.31 | +13.69 |
| Perfeito quarto (F) | 25?12 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 12√32 | 1.334 | 500. | 4?3 - 1.33333... | 498.04 | +1.96 |
| Tritone (G♭) | 26?12 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = √2 | 1.4142 | 600 | 64?45- 1.42222... | 609.78 | -9.78 |
| Quinta perfeita (G) | 27?12 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 12√128 | 1.49807 | 700 | 3?2 = 1,5 | 701,9 | - Sim. |
| Menor sexto (A♭) | 28?12 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 3√4 | 1.587401 | 800 | 8?5 = 1,6 | 813.69 | -13.69 |
| Major sexto (A) | 29?12 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 4√8 | 1.68179 | 900 | 5?3 - 1.66666... | 884.36 | +15.64 |
| Sétima menor (B♭) | 210.?12 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 6√32 | 1.78171797 | 1000 | 16.?9 - 1.77777... | 996.09 | +3.91 |
| Major sétimo (B) | 211?12 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 12√2048 | 1.8877 | 1100 | 15?8= 1.875 | 1088.270 | +11.73 |
| Oitava (C) | 212?12 = 2 | 2 | 1200 | 2?1 = 2 | 120. | 0 |
Divisão igual de sete tons da quinta
Violinos, violas e violoncelos são afinados em quintas perfeitas (G–D–A–E para violinos e C–G–D–A para violas e violoncelos), o que sugere que sua relação de semitons é ligeiramente maior do que em convencionais temperamento igual de 12 tons. Como uma quinta perfeita está em relação 3:2 com seu tom de base, e esse intervalo compreende sete passos, cada tom está na proporção de 7√3⁄2 para o próximo (100,28 centavos), o que fornece uma perfeita quinta com proporção de 3:2, mas uma oitava ligeiramente ampliada com uma proporção de ≈ 517:258 ou ≈ 2,00388:1 em vez do usual 2:1, porque 12 quintas perfeitas não são iguais a sete oitavas. Durante a execução real, no entanto, o violinista escolhe as notas de ouvido, e apenas as quatro notas contínuas das cordas exibem essa proporção de 3:2.
Outros temperamentos iguais
Temperamentos de cinco, sete e nove tons em etnomusicologia
Temperament igual de cinco e sete tons (5. ![]() Jogar(help·info) e 7-TET
Jogar(help·info) e 7-TET![]() Jogar(help·info)), com 240-
Jogar(help·info)), com 240- ![]() Jogar(help·info) e 171-cent
Jogar(help·info) e 171-cent ![]() Jogar(help·info) passos, respectivamente, são bastante comuns.
Jogar(help·info) passos, respectivamente, são bastante comuns.
5-TET e 7-TET marcam os pontos finais da faixa de afinação válida do temperamento sintônico, conforme mostrado na Figura 1.
- Em 5-TET, o quinto perfeito temperado é de 720 centavos de largura (no topo do continuum de ajuste), e marca o ponto final no continuum de ajuste no qual a largura do segundo menor se reduz a uma largura de 0 centavos.
- Em 7-TET, o quinto perfeito temperado é 686 centavos de largura (na parte inferior do continuum de ajuste), e marca o ponto final no continuum de ajuste, no qual o segundo menor se expande para ser tão largo quanto o segundo maior (a 171 centavos cada).
Temperamento igual de 5 tons e 9 tons
De acordo com Kunst (1949), os gamelans indonésio são sintonizados com 5-TET, mas de acordo com Hood (1966) e McPhee (1966) sua afinação varia amplamente, e de acordo com Tenzer (2000) eles contêm oitavas alongadas. Agora aceita-se que dos dois sistemas de afinação primária na música gamelan, slendro e pelog, apenas slendro um pouco se assemelha a temperamento igual de cinco tons, enquanto pelog é altamente desigual; no entanto, Surjodiningrat et al. (1972) analisar pelog como equivalente a 9-TET (133-cent passos ![]() Jogar(help·info)).
Jogar(help·info)).
Temperamento igual de 7 tons
A Xilofone tailandês medido por Morton (1974) "variou apenas mais ou menos 5 centavos" de 7-TET. De acordo com Morton, "os instrumentos tailandeses de arremesso fixo são ajustados a um sistema equidistante de sete arremessos por oitava... Como na música tradicional ocidental, no entanto, todos os arremessos do sistema de afinação não são usados em um modo (muitas vezes referido como 'escala'); no sistema tailandês cinco dos sete são usados em arremessos principais em qualquer modo, estabelecendo assim um padrão de intervalos não-distantes para o modo." ![]() Jogar(help·info)
Jogar(help·info)
Uma escala indígena sul-americana de uma cultura pré-instrumental medida por Boiles (1969) apresentava um temperamento igual de sete tons de 175 centavos, que alongava ligeiramente a oitava, como na música instrumental de gamelão.
A música chinesa tradicionalmente usa o 7-TET.
Vários temperamentos iguais
Muitos instrumentos foram construídos usando afinação 19 EDO. Aproximadamente equivalente a 1/3 de vírgula, tem uma quinta perfeita ligeiramente mais achatada (a 695 centavos), mas sua terça menor e sexta maior estão a menos de um quinto de um centavo de apenas. (O EDO mais baixo que produz uma terça menor e uma sexta maior melhores do que 19 EDO é 232 EDO). 39;s.
23 EDO é o maior EDO que falha em aproximar o 3º, 5º, 7º e 11º harmônicos (3:2, 5:4, 7:4, 11:8) dentro de 20 centavos. Mas ele faz relações aproximadas entre eles (incluindo a terça menor 6/5 justamente afinada) muito bem, tornando-o atraente para microtonalistas que buscam um território harmônico incomum.
24 EDO, a escala de um quarto de tom, é particularmente popular, pois representa um ponto de acesso conveniente para compositores condicionados nas práticas de afinação e notação Western 12 EDO padrão que também estão interessados em microtonalidade. Como 24 EDO contém todas as notas de 12 EDO, os músicos empregam as cores adicionais sem perder nenhuma tática disponível na harmonia de 12 tons. O fato de 24 ser um múltiplo de 12 também torna fácil obter 24 EDO instrumentalmente, empregando dois instrumentos tradicionais de 12 EDO afinados em um quarto de tom, como dois pianos, o que também permite que cada intérprete (ou um intérprete tocando um piano diferente com cada mão) para ler a notação familiar de 12 tons. Vários compositores, incluindo Charles Ives, experimentaram música para pianos de quarto de tom. 24 EDO também se aproxima muito bem do 11º e 13º harmônicos, ao contrário do 12 EDO.
26 EDO é o menor EDO para sintonizar quase puramente o 7º harmônico (7:4). É também um temperamento significativo, embora muito plano, com quatro de suas quintas perfeitas produzindo uma terça neutra em vez de uma terça maior. 26 EDO tem duas terças menores e duas sextas menores e pode ser um temperamento alternativo para a harmonia da barbearia.
27 EDO é o menor EDO que representa exclusivamente todos os intervalos envolvendo os oito primeiros harmônicos. Tempera a vírgula septimal, mas não a vírgula sintônica.
29 é o menor número de divisões iguais da oitava que produz uma quinta perfeita melhor que 12 EDO. Sua terça maior é quase tão imprecisa quanto 12 EDO, mas é afinada em 14 centavos bemol em vez de 14 centavos em ponto. Ele também afina o 7º, 11º e 13º harmônicos bemol, aproximadamente na mesma quantidade. Isso significa que intervalos como 7:5, 11:7, 13:11, etc., são todos combinados extremamente bem em 29 EDO.
31 EDO foi defendido por Christiaan Huygens e Adriaan Fokker e representa uma excelente aproximação do significado de um quarto de vírgula. 31 EDO tem uma quinta um pouco menos precisa do que 12 EDO, mas fornece terças maiores quase puras e sextas menores (menos de um centavo de apenas) e correspondências decentes para harmônicos até pelo menos 13, dos quais o sétimo harmônico é particularmente preciso.
34 EDO fornece um pouco menos de erros totais combinados de aproximação para os limites de 5 razões apenas 3:2, 5:4, 6:5 e suas inversões do que 31 EDO, embora a aproximação de 5:4 seja pior. 34 EDO não aproxima proporções envolvendo 7 poços. Ele contém um trítono de 600 centavos, já que é um EDO de número par.
41 EDO é o segundo menor número de divisões iguais que produz uma quinta perfeita melhor que 12 EDO. Sua terça maior é mais precisa do que 12 EDO e 29 EDO, cerca de seis centavos de dólar. Não é um significado, então distingue 10:9 e 9:8, ao contrário de 31 EDO. É mais preciso em 13 limites do que em 31 EDO.
46 EDO fornece terças maiores e quintas perfeitas levemente sustenidas, dando às tríades um som brilhante característico. Os harmônicos até 11 estão dentro de cinco centavos de precisão, com 10:9 e 9:5 um quinto de centésimo de distância do puro. Como não é um sistema de meio tom, ele distingue 10:9 e 9:8.
53 EDO teve apenas uso ocasional, mas é melhor em aproximar as consonâncias justas tradicionais do que 12, 19 ou 31 EDO. Suas quintas perfeitas extremamente boas o tornam intercambiável com uma afinação pitagórica estendida, mas também acomoda o temperamento cismático e às vezes é usado na teoria musical turca. No entanto, não se encaixa nos requisitos dos temperamentos médios, que colocam boas terças ao alcance fácil por meio do ciclo de quintas. Em 53 EDO, as próprias terças consonantais são alcançadas usando uma quarta diminuta pitagórica (C-F♭), pois é um exemplo de temperamento cismático, como 41 EDO.
72 EDO aproxima bem muitos intervalos de entonação justa, fornecendo equivalentes quase justos para o 3º, 5º, 7º e 11º harmônicos. 72 EDO foi ensinado, escrito e executado na prática por Joe Maneri e seus alunos (cujas inclinações atonais normalmente evitam qualquer referência a qualquer entonação). Pode ser considerado uma extensão de 12 EDO porque 72 é um múltiplo de 12. 72 EDO tem um menor intervalo seis vezes menor que o menor intervalo de 12 EDO e, portanto, contém seis cópias de 12 EDO começando em alturas diferentes. Ele também contém três cópias de 24 EDO e duas cópias de 36 EDO, que são múltiplos de 12 EDO.
96 EDO aproxima todos os intervalos dentro de 6,25 centavos, o que é quase imperceptível. Como um múltiplo óctuplo de 12, pode ser usado totalmente como o 12 EDO comum. Tem sido defendido por vários compositores, especialmente Julián Carrillo.
Outras divisões iguais da oitava que encontraram uso ocasional incluem 15 EDO, 17 EDO e 22 EDO.
2, 5, 12, 41, 53, 306, 665 e 15601 são denominadores dos primeiros convergentes de log2(3), então 2, 5, 12, 41, 53, 306, 665 e 15601 duodécimos (e quintos), sendo em temperamentos iguais correspondentes iguais a um número inteiro de oitavas, são melhores aproximações de 2, 5, 12, 41, 53, 306, 665 e 15601 apenas doze décimos/quintos do que em qualquer temperamento igual com menos tons.
1, 2, 3, 5, 7, 12, 29, 41, 53, 200... (sequência A060528 no OEIS) é a sequência de divisões de oitava que fornece aproximações cada vez melhores da quinta justa. As sequências relacionadas contêm divisões que aproximam outros intervalos justos.
Temperamentos iguais de intervalos não-oitavos
A versão igual-temperada da escala Bohlen-Pierce consiste na relação 3:1, 1902 centavos, convencionalmente um quinto perfeito mais uma oitava (isto é, um duodécimo perfeito), chamado nesta teoria uma tritave (![]() jogar(help·info)), e dividir em 13 partes iguais. Isso fornece uma combinação muito próxima de razões justly ajustadas que consistem apenas em números ímpares. Cada passo é de 146,3 centavos (
jogar(help·info)), e dividir em 13 partes iguais. Isso fornece uma combinação muito próxima de razões justly ajustadas que consistem apenas em números ímpares. Cada passo é de 146,3 centavos (![]() jogar(help·info)), ou 13√3.
jogar(help·info)), ou 13√3.
Wendy Carlos criou três temperamentos iguais incomuns após um estudo minucioso das propriedades de possíveis temperamentos com tamanho de passo entre 30 e 120 centavos. Estes foram chamados de alfa, beta e gama. Eles podem ser considerados divisões iguais da quinta perfeita. Cada um deles fornece uma aproximação muito boa de vários intervalos justos. Seus tamanhos de passo:
- alfa: 9√3?2 (78,0 centavos)
 Jogar(help·info)
Jogar(help·info) - Não.: 11√3?2 (63,8 centavos)
 Jogar(help·info)
Jogar(help·info) - Gamma: 20.√3?2 (35,1 centavos)
 Jogar(help·info)
Jogar(help·info)
Alpha e Beta podem ser ouvidos na faixa-título do álbum de Carlos, de 1986, Beauty in the Beast.
Proporções entre o semitom e o tom inteiro
Nesta seção, semitom e tom inteiro podem não ter seus significados 12-EDO usuais, pois discute como eles podem ser temperados de maneiras diferentes de suas versões justas para produzir relacionamentos desejados. Seja o número de passos em um semitom s, e o número de passos em um tom seja t.
Existe exatamente uma família de temperamentos iguais que fixa o semitom em qualquer fração adequada de um tom inteiro, mantendo as notas na ordem correta (o que significa que, por exemplo, C, D, E, F e F♯ estão em ordem crescente se preservam suas relações usuais com C). Ou seja, fixar q a uma fração própria na relação qt = s também define uma família única de um temperamento igual e seus múltiplos que preenchem este relacionamento.
Por exemplo, onde k é um número inteiro, 12k-EDO define q = 1⁄2 e 19k-EDO conjuntos q = 1⁄3. Os menores múltiplos nessas famílias (por exemplo, 12 e 19 acima) têm a propriedade adicional de não ter notas fora do círculo de quintas. (Isto não é verdade em geral; em 24-EDO, os meios sustenidos e meios bemóis não estão no círculo de quintas gerado a partir de C.) Os casos extremos são 5k-EDO, onde q = 0 e o semitom se torna um uníssono, e 7k-EDO, onde q = 1 e o semitom e o tom são iguais intervalo.
Uma vez que se sabe quantos passos um semitom e um tom estão neste temperamento igual, pode-se encontrar o número de passos que ele tem na oitava. Um temperamento igual com as propriedades acima (incluindo não ter notas fora do círculo de quintas) divide a oitava em 7t − 2s passos e a quinta perfeita em 4t − s passos. Se houver notas fora do círculo de quintas, deve-se então multiplicar esses resultados por n, o número de círculos de quintas não sobrepostos necessários para gerar todas as notas (por exemplo, dois em 24-EDO, seis em 72-EDO). (Deve-se usar o semitom pequeno para esse propósito: 19-EDO tem dois semitons, sendo um 1⁄3 tom e o outro sendo 2⁄3.)
A menor dessas famílias é 12k-EDO e, em particular, 12-EDO é o menor temperamento igual com as propriedades acima. Além disso, torna o semitom exatamente meio tom inteiro, a relação mais simples possível. Estas são algumas das razões pelas quais o 12-EDO se tornou o temperamento igual mais comumente usado. (Outra razão é que 12-EDO é o menor temperamento igual para se aproximar da harmonia de 5 limites, sendo o segundo menor 19-EDO.)
Cada escolha de fração q para a relação resulta em exatamente uma família de temperamento igual, mas o inverso não é verdadeiro: 47-EDO tem dois semitons diferentes, onde um é 1⁄7 tom e o outro é 8⁄9, que não são complementares entre si como em 19-EDO (1⁄3 e 2⁄3). Pegar cada semitom resulta em uma escolha diferente de quinta justa.
Sistemas de ajuste relacionados
Afinações diatônicas regulares
A afinação diatônica em doze iguais pode ser generalizada para qualquer afinação diatônica regular dividindo a oitava como uma sequência de passos TTSTTTS (ou uma rotação dela) com todos os T's e todos os S's mesmo tamanho e os S's menores que os T's. Em doze iguais, o S é o semitom e tem exatamente a metade do tamanho do tom T. Quando os S's reduzem a zero, o resultado é TTTTT, um temperamento igual de cinco tons. À medida que os semitons aumentam, eventualmente os passos são todos do mesmo tamanho e o resultado é um temperamento igual de sete tons. Esses dois pontos finais não estão incluídos como afinações diatônicas regulares.
As notas em uma afinação diatônica regular são conectadas por um ciclo de sete quintas temperadas. O sistema de 12 tons generaliza de forma semelhante a uma sequência CDCDDCDCDCDD (ou uma rotação dela) de semitons cromáticos e diatônicos conectados por um ciclo de 12 quintas. Nesse caso, sete iguais são obtidos no limite quando o tamanho de C tende a zero, e cinco iguais são o limite quando D tende a zero, enquanto doze iguais é, obviamente, o caso C = D.
Alguns dos tamanhos intermediários de tons e semitons também podem ser gerados em sistemas de temperamento igual. Por exemplo, se o semitom diatônico é o dobro do tamanho do semitom cromático, ou seja, D = 2C, o resultado é igual a dezenove, com um passo para o semitom cromático, dois passos para o semitom diatônico, três passos para o tom e o número total de passos 5T + 2S = 15 + 4 = 19 passos. O sistema de 12 tons resultante aproxima-se do historicamente importante significado de vírgula de 1/3.
Se o semitom cromático é dois terços do tamanho do semitom diatônico, ou seja, C = (2/3)D, o resultado é 31 igual, com dois passos para o semitom cromático, três passos para o semitom diatônico e cinco passos para o tom, onde 5T + 2S = 25 + 6 = 31 passos. O sistema de 12 tons resultante se aproxima do historicamente importante significado de vírgula de 1/4.
Contenido relacionado
Número de Bernoulli
Campo algebricamente fechado
Curtose


![{displaystyle r={sqrt[{n}]{p}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b55fb394d767c50fb569ca27fd636072c72fbd7c)



![{displaystyle {sqrt[{12}]{2}}=2^{frac {1}{12}}approx 1.059463}](https://wikimedia.org/api/rest_v1/media/math/render/svg/232c2beab28b1c46c328080d982595d9ef196e08)
![{displaystyle P_{n}=P_{a}left({sqrt[{12}]{2}}right)^{(n-a)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3381e111c79f7e16a073bbe05c6cabeaba2ff79a)
![{displaystyle P_{40}=440left({sqrt[{12}]{2}}right)^{(40-49)}approx 261.626 mathrm {Hz} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f16dc9af5bbe778786f73eca304c80c72584cd70)
![{displaystyle P_{46}=440left({sqrt[{12}]{2}}right)^{(46-49)}approx 369.994 mathrm {Hz} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c7144b8e3148077acb97a47d384a62a1f2a5445)





