Sistema de coordenada cartesiana
Na geometria, um sistema de coordenadas cartesianas (,) em um plano é um sistema de coordenadas que especifica cada ponto exclusivamente por um par de números reais chamados coordenadas, que são as distâncias assinaladas ao ponto a partir de duas linhas perpendiculares fixas orientadas, denominadas linhas de coordenadas, eixos de coordenadas ou apenas eixos (plural de eixo) do sistema. O ponto onde eles se encontram é chamado de origem e tem (0, 0) como coordenadas.
Da mesma forma, a posição de qualquer ponto no espaço tridimensional pode ser especificada por três coordenadas cartesianas, que são as distâncias sinalizadas do ponto a três planos mutuamente perpendiculares. Mais geralmente, n coordenadas cartesianas especificam o ponto em um n espaço euclidiano -dimensional para qualquer dimensão n. Essas coordenadas são as distâncias sinalizadas do ponto para n hiperplanos fixos mutuamente perpendiculares.

As coordenadas cartesianas são nomeadas em homenagem a René Descartes, cuja invenção no século XVII revolucionou a matemática ao fornecer o primeiro elo sistemático entre geometria e álgebra. Usando o sistema de coordenadas cartesianas, formas geométricas (como curvas) podem ser descritas por equações envolvendo as coordenadas dos pontos da forma. Por exemplo, um círculo de raio 2, centrado na origem do plano, pode ser descrito como o conjunto de todos os pontos cujas coordenadas x e y satisfaça a equação x2 + y2 = 4.
As coordenadas cartesianas são a base da geometria analítica e fornecem interpretações geométricas esclarecedoras para muitos outros ramos da matemática, como álgebra linear, análise complexa, geometria diferencial, cálculo multivariado, teoria de grupos e muito mais. Um exemplo familiar é o conceito do gráfico de uma função. As coordenadas cartesianas também são ferramentas essenciais para a maioria das disciplinas aplicadas que lidam com geometria, incluindo astronomia, física, engenharia e muito mais. Eles são o sistema de coordenadas mais comum usado em computação gráfica, desenho geométrico auxiliado por computador e outros processamentos de dados relacionados à geometria.
História
O adjetivo Cartesiano refere-se ao matemático e filósofo francês René Descartes, que publicou essa ideia em 1637 enquanto residia na Holanda. Foi descoberto independentemente por Pierre de Fermat, que também trabalhou em três dimensões, embora Fermat não tenha publicado a descoberta. A clériga francesa Nicole Oresme usava construções semelhantes às coordenadas cartesianas bem antes da época de Descartes e Fermat.
Tanto Descartes quanto Fermat usaram um único eixo em seus tratamentos e têm um comprimento variável medido em referência a esse eixo. O conceito de usar um par de eixos foi introduzido mais tarde, após a descoberta de Descartes. La Géométrie foi traduzido para o latim em 1649 por Frans van Schooten e seus alunos. Esses comentaristas introduziram vários conceitos ao tentar esclarecer as ideias contidas na obra de Descartes.
O desenvolvimento do sistema de coordenadas cartesianas desempenharia um papel fundamental no desenvolvimento do cálculo por Isaac Newton e Gottfried Wilhelm Leibniz. A descrição de duas coordenadas do plano foi posteriormente generalizada no conceito de espaços vetoriais.
Muitos outros sistemas de coordenadas foram desenvolvidos desde Descartes, como as coordenadas polares para o plano e as coordenadas esféricas e cilíndricas para o espaço tridimensional.
Descrição
Uma dimensão
Escolher um sistema de coordenadas cartesianas para um espaço unidimensional - isto é, para uma linha reta - envolve escolher um ponto O da linha (a origem), uma unidade de comprimento e um orientação para a linha. Uma orientação escolhe qual das duas meias-linhas determinadas por O é a positiva e qual é a negativa; dizemos então que a linha "está orientada" (ou "pontos") da metade negativa para a metade positiva. Então cada ponto P da linha pode ser especificado por sua distância de O, tomada com um sinal + ou − dependendo de qual meia-linha contém P.
Uma linha com um sistema cartesiano escolhido é chamada de linha numérica. Cada número real tem uma localização única na linha. Por outro lado, cada ponto na linha pode ser interpretado como um número em um continuum ordenado, como os números reais.
Duas dimensões
Um sistema de coordenadas cartesianas em duas dimensões (também chamado de sistema de coordenadas retangulares ou sistema de coordenadas ortogonais) é definido por um par ordenado de linhas perpendiculares (eixos), uma única unidade de comprimento para ambos os eixos e uma orientação para cada eixo. O ponto onde os eixos se encontram é tomado como origem para ambos, transformando cada eixo em uma linha numérica. Para qualquer ponto P, uma linha é desenhada através de P perpendicular a cada eixo, e a posição onde encontra o eixo é interpretada como um número. Os dois números, nessa ordem escolhida, são as coordenadas cartesianas de P. A construção inversa permite determinar o ponto P dadas as suas coordenadas.
A primeira e a segunda coordenadas são chamadas de abcissa e ordenada de P, respectivamente; e o ponto onde os eixos se encontram é chamado de origem do sistema de coordenadas. As coordenadas geralmente são escritas como dois números entre parênteses, nessa ordem, separados por vírgula, como em (3, −10.5). Assim, a origem tem coordenadas (0, 0), e os pontos nos semi-eixos positivos, a uma unidade de distância da origem, têm coordenadas (1, 0) e (0, 1).
Em matemática, física e engenharia, o primeiro eixo é geralmente definido ou representado como horizontal e orientado para a direita, e o segundo eixo é vertical e orientado para cima. (Entretanto, em alguns contextos de computação gráfica, o eixo das ordenadas pode ser orientado para baixo.) A origem geralmente é rotulada como O e as duas coordenadas geralmente são indicadas pelas letras X e Y, ou x e y. Os eixos podem então ser chamados de eixo X e eixo Y. As escolhas de letras vêm da convenção original, que é usar a última parte do alfabeto para indicar valores desconhecidos. A primeira parte do alfabeto foi usada para designar valores conhecidos.
Um plano euclidiano com um sistema de coordenadas cartesiano escolhido é chamado de plano cartesiano . Num plano cartesiano pode-se definir representantes canônicos de certas figuras geométricas, como o círculo unitário (com raio igual à unidade de comprimento e centro na origem), o quadrado unitário (cuja diagonal tem extremidades em (0, 0) e (1, 1)), a hipérbole da unidade e assim por diante.
Os dois eixos dividem o plano em quatro ângulos retos, chamados quadrantes. Os quadrantes podem ser nomeados ou numerados de várias maneiras, mas o quadrante onde todas as coordenadas são positivas é geralmente chamado de primeiro quadrante.
Se as coordenadas de um ponto são (x, y), então suas distâncias do O eixo X e do eixo Y são |y| e |x|, respectivamente; onde | · | denota o valor absoluto de um número.
Três dimensões
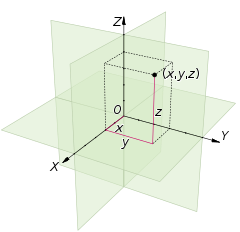
Um sistema de coordenadas cartesianas para um espaço tridimensional consiste em um trio ordenado de linhas (os eixos) que passam por um ponto comum (a origem) e são perpendiculares aos pares; uma orientação para cada eixo; e uma única unidade de comprimento para todos os três eixos. Como no caso bidimensional, cada eixo se torna uma linha numérica. Para qualquer ponto P do espaço, considera-se um hiperplano através de P perpendicular a cada eixo de coordenadas, e interpreta-se o ponto onde esse hiperplano corta o eixo como um número. As coordenadas cartesianas de P são esses três números, na ordem escolhida. A construção inversa determina o ponto P dadas suas três coordenadas.
Alternativamente, cada coordenada de um ponto P pode ser tomada como a distância de P ao hiperplano definido pelos outros dois eixos, com o sinal determinado pela orientação do eixo correspondente.
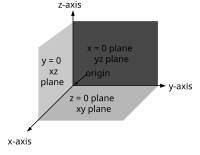
Cada par de eixos define um hiperplano de coordenadas. Esses hiperplanos dividem o espaço em oito oitantes. Os octantes são:
As coordenadas geralmente são escritas como três números (ou fórmulas algébricas) entre parênteses e separados por vírgulas, como em (3, −2.5, 1) ou (t, u + v, π/2). Assim, a origem tem coordenadas (0, 0, 0), e os pontos unitários nos três eixos são (1, 0, 0) , (0, 1, 0) e (0, 0, 1).
Não há nomes padrão para as coordenadas nos três eixos (no entanto, às vezes são usados os termos abcissa, ordenada e aplicar). As coordenadas geralmente são indicadas pelas letras X, Y e Z ou x, y e z. Os eixos podem então ser chamados de eixo X, eixo Y e eixo Z, respectivamente. Em seguida, os hiperplanos de coordenadas podem ser chamados de plano XY, plano YZ e plano XZ.
Em contextos de matemática, física e engenharia, os dois primeiros eixos são geralmente definidos ou representados como horizontais, com o terceiro eixo apontando para cima. Nesse caso, a terceira coordenada pode ser chamada de altura ou altitude. A orientação é geralmente escolhida de modo que o ângulo de 90 graus do primeiro eixo ao segundo eixo pareça anti-horário quando visto do ponto (0, 0, 1); uma convenção comumente chamada de regra da mão direita.

Dimensões superiores
Uma vez que as coordenadas cartesianas são únicas e não ambíguas, os pontos de um avião cartesiano podem ser identificados com pares de números reais; isto é, com o produto cartesiano R2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =R× × R{displaystyle mathbb Não. {R} times mathbb Não., onde R{displaystyle mathbb {R} } } é o conjunto de todos os números reais. Da mesma forma, os pontos em qualquer espaço euclidiano de dimensão n ser identificado com as tuplas (listas) de n números reais; isto é, com o produto cartesiano Rn{displaystyle mathbb {R} ^{n}}.
Generalizações
O conceito de coordenadas cartesianas se generaliza para permitir eixos que não são perpendiculares entre si e/ou unidades diferentes ao longo de cada eixo. Nesse caso, cada coordenada é obtida projetando o ponto em um eixo ao longo de uma direção paralela ao outro eixo (ou, em geral, ao hiperplano definido por todos os outros eixos). Nesse sistema de coordenadas oblíquas, os cálculos de distâncias e ângulos devem ser modificados em relação aos sistemas cartesianos padrão, e muitas fórmulas padrão (como a fórmula pitagórica para a distância) não são válidas (consulte plano afim).
Notações e convenções
As coordenadas cartesianas de um ponto geralmente são escritas entre parênteses e separadas por vírgulas, como em (10, 5) ou (3, 5, 7). A origem geralmente é marcada com a letra maiúscula O. Na geometria analítica, coordenadas desconhecidas ou genéricas são muitas vezes indicadas pelas letras (x, y) no plano e (x, y, z) no espaço tridimensional. Esse costume vem de uma convenção da álgebra, que usa letras próximas ao final do alfabeto para valores desconhecidos (como as coordenadas de pontos em muitos problemas geométricos) e letras próximas ao início para determinadas quantidades.
Esses nomes convencionais são frequentemente usados em outros domínios, como física e engenharia, embora outras letras possam ser usadas. Por exemplo, em um gráfico que mostra como uma pressão varia com o tempo, as coordenadas do gráfico podem ser denotadas como p e t. Cada eixo geralmente recebe o nome da coordenada que é medida ao longo dele; então se diz o eixo x, o eixo y, o eixo t, etc.
Outra convenção comum para nomeação de coordenadas é usar subscritos, como (x1, x2,..., xn) para as coordenadas n em um n- espaço dimensional, especialmente quando n é maior que 3 ou não especificado. Alguns autores preferem a numeração (x0, x1,..., xn−1). Essas notações são especialmente vantajosas na programação de computadores: ao armazenar as coordenadas de um ponto como uma matriz, em vez de um registro, o subscrito pode servir para indexar as coordenadas.
Em ilustrações matemáticas de sistemas cartesianos bidimensionais, a primeira coordenada (tradicionalmente chamada de abcissa) é medida ao longo de um eixo horizontal, orientado da esquerda para a direita. A segunda coordenada (a ordenada) é então medida ao longo de um eixo vertical, geralmente orientado de baixo para cima. As crianças pequenas que estão aprendendo o sistema cartesiano geralmente aprendem a ordem de leitura dos valores antes de consolidar os conceitos dos eixos x-, y- e z, começando com mnemônicos 2D (por exemplo, 'Caminhe ao longo do corredor e depois suba as escadas' semelhante a uma linha reta no eixo x e suba verticalmente ao longo do y-eixo).
Gráficos de computador e processamento de imagem, no entanto, geralmente usam um sistema de coordenadas com o eixo y orientado para baixo na tela do computador. Essa convenção se desenvolveu na década de 1960 (ou antes) a partir da maneira como as imagens eram originalmente armazenadas em buffers de exibição.
Para sistemas tridimensionais, uma convenção é retratar o plano xy horizontalmente, com o eixo z adicionado para representar a altura (positivo para cima). Além disso, existe uma convenção para orientar o eixo x em direção ao visualizador, inclinado para a direita ou para a esquerda. Se um diagrama (projeção 3D ou desenho em perspectiva 2D) mostra os eixos x e y horizontalmente e verticalmente, respectivamente, então o z- eixo deve ser mostrado apontando "para fora da página" em direção ao visualizador ou câmera. Nesse diagrama 2D de um sistema de coordenadas 3D, o eixo z apareceria como uma linha ou raio apontando para baixo e para a esquerda ou para baixo e para a direita, dependendo do visualizador presumido ou da perspectiva da câmera. Em qualquer diagrama ou exibição, a orientação dos três eixos, como um todo, é arbitrária. No entanto, a orientação dos eixos em relação um ao outro deve sempre obedecer à regra da mão direita, a menos que especificamente indicado de outra forma. Todas as leis da física e da matemática pressupõem essa destreza, o que garante a consistência.
Para diagramas 3D, os nomes "abscissa" e "ordenada" raramente são usados para x e y, respectivamente. Quando são, a coordenada z é às vezes chamada de aplicada. As palavras abscissa, ordenada e aplicar às vezes são usadas para se referir a eixos de coordenadas em vez de valores de coordenadas.
Quadrantes e octantes
Os eixos de um sistema cartesiano bidimensional dividem o plano em quatro regiões infinitas, chamadas quadrantes, cada uma limitada por dois semi-eixos. Estes são frequentemente numerados de 1 a 4 e indicados por algarismos romanos: I (onde ambas as coordenadas têm sinais positivos), II (onde a abscissa é negativa − e a ordenada é positiva +), III (onde tanto a abscissa quanto a ordenada são −), e IV (abscissa +, ordenada −). Quando os eixos são desenhados de acordo com o costume matemático, a numeração vai no sentido anti-horário começando no quadrante superior direito ("nordeste").
Da mesma forma, um sistema cartesiano tridimensional define uma divisão do espaço em oito regiões ou oitantes, de acordo com os sinais das coordenadas dos pontos. A convenção usada para nomear um octante específico é listar seus signos; por exemplo, (+ + +) ou (− + −). A generalização do quadrante e octante para um número arbitrário de dimensões é o orthant, e um sistema de nomenclatura semelhante se aplica.
Fórmulas cartesianas para o plano
Distância entre dois pontos
A distância euclidiana entre dois pontos do avião com coordenadas cartesianas (x1,Sim.1)(x_{1},y_{1})} e (x2,Sim.2)(x_{2},y_{2})} o
Esta é a versão cartesiana do teorema de Pitágoras. No espaço tridimensional, a distância entre pontos (x1,Sim.1,zangão.1)(x_{1},y_{1},z_{1})} e (x2,Sim.2,zangão.2)(x_{2},y_{2},z_{2})} o
que pode ser obtido por duas aplicações consecutivas de Pitágoras' teorema.
Transformações euclidianas
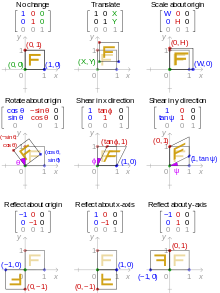
As transformações euclidianas ou movimentos euclidianos são os mapeamentos (bijetivos) de pontos do plano euclidiano para si mesmos que preservam as distâncias entre os pontos. Existem quatro tipos desses mapeamentos (também chamados de isometrias): translações, rotações, reflexões e reflexões deslizantes.
Tradução
Traduzir um conjunto de pontos do plano, preservando as distâncias e direções entre eles, equivale a somar um par fixo de números (a, b) para as coordenadas cartesianas de cada ponto do conjunto. Ou seja, se as coordenadas originais de um ponto forem (x, y), após a translação elas serão
Rotação
Para girar uma figura anti-horário em torno da origem por algum ângulo θ θ - Sim. é equivalente a substituir cada ponto por coordenadas (x,Sim.) pelo ponto com coordenadas (x ',Sim. '), onde
Assim:
Reflexão
Se (x, Sim.) são as coordenadas cartesianas de um ponto, então (x, Sim.) são as coordenadas de sua reflexão através do segundo eixo de coordenadas (o eixo y), como se essa linha fosse um espelho. Igualmente. (x,Sim.) são as coordenadas de sua reflexão através do primeiro eixo de coordenadas (o eixo x). Em mais generalidade, reflexão através de uma linha através da origem fazendo um ângulo θ θ - Sim. com o eixo x, é equivalente a substituir cada ponto com coordenadas (x, Sim.) pelo ponto com coordenadas (x′,Sim.′), onde
Assim:
Reflexão deslizante
Uma reflexão deslizante é a composição de uma reflexão através de uma linha seguida por uma translação na direção dessa linha. Vê-se que a ordem dessas operações não importa (a tradução pode vir primeiro, seguida da reflexão).
Forma matricial geral das transformações
Todas as transformações afinas do avião podem ser descritas de forma uniforme usando matrizes. Com esta finalidade as coordenadas (x,Sim.)(x,y)} de um ponto são comumente representados como a matriz da coluna (xSim.).{displaystyle {begin{pmatrix}xyend{pmatrix}}.} O resultado (x?,Sim.?)(x',y')} de aplicar uma transformação de affine a um ponto (x,Sim.)(x,y)} é dada pela fórmula
Entre as transformações afinas, as transformações euclidianas são caracterizadas pelo fato de que a matriz ANão. A. é ortogonal; isto é, suas colunas são vetores ortogonais da norma euclidiana, ou, explicitamente,
Isto é equivalente a dizer que A vezes sua transposição é a matriz identidade. Se essas condições não forem válidas, a fórmula descreve uma transformação afim mais geral.
A transformação é uma tradução se e somente se A é a matriz de identidade. A transformação é uma rotação em torno de algum ponto se e somente se A é uma matriz de rotação, o que significa que é ortogonal e
Uma reflexão ou reflexão deslizante é obtida quando,
Assumindo que as traduções não são usadas (isto é, b)1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =b)2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0Não. b_{1}=b_{2}=0}) as transformações podem ser compostas simplesmente multiplicando as matrizes de transformação associadas. No caso geral, é útil usar a matriz aumentada da transformação; isto é, reescrever a fórmula de transformação
Transformação afim
Transformações afins do plano euclidiano são transformações que mapeiam linhas em linhas, mas podem alterar distâncias e ângulos. Como dito na seção anterior, eles podem ser representados com matrizes aumentadas:
As transformações euclidianas são as transformações affine tais que a matriz 2×2 da AEu...,JJNão. A_{i,j}} é ortogonal.
A matriz aumentada que representa a composição de duas transformações afins é obtida pela multiplicação de suas matrizes aumentadas.
Algumas transformações afins que não são transformações euclidianas receberam nomes específicos.
Escalonamento
Um exemplo de uma transformação afim que não é euclidiana é dado por escala. Aumentar ou diminuir uma figura equivale a multiplicar as coordenadas cartesianas de cada ponto pelo mesmo número positivo m. Se (x, y) são as coordenadas de um ponto na figura original, o ponto correspondente na figura em escala tem coordenadas
Se m for maior que 1, a figura se torna maior; se m estiver entre 0 e 1, ele se torna menor.
Tosquia
Uma transformação de cisalhamento empurrará o topo de um quadrado para o lado para formar um paralelogramo. O cisalhamento horizontal é definido por:
O cisalhamento também pode ser aplicado verticalmente:
Orientação e lateralidade
Em duas dimensões
Fixar ou escolher o eixo x determina a direção do eixo y. Ou seja, o eixo y é necessariamente a perpendicular ao eixo x através do ponto marcado como 0 no eixo x. Mas há uma escolha de qual das duas meias linhas na perpendicular designar como positiva e qual como negativa. Cada uma dessas duas opções determina uma orientação diferente (também chamada de lateralidade) do plano cartesiano.
A maneira usual de orientar o plano, com o eixo x positivo apontando para a direita e o eixo y positivo apontando para cima (e o eixo x sendo o eixo i> o "primeiro" e o eixo y o "segundo" eixo), é considerado o eixo positivo ou orientação padrão, também chamada de orientação destra.
Um mnemônico comumente usado para definir a orientação positiva é a regra da mão direita. Colocando a mão direita um tanto fechada no plano com o polegar apontando para cima, os dedos apontam do eixo x para o eixo y, em um sistema de coordenadas positivamente orientado.
A outra forma de orientar o plano é seguir a regra da mão esquerda, colocando a mão esquerda no plano com o polegar apontando para cima.
Ao apontar o polegar para longe da origem ao longo de um eixo em direção ao positivo, a curvatura dos dedos indica uma rotação positiva ao longo desse eixo.
Independentemente da regra usada para orientar o plano, girar o sistema de coordenadas preservará a orientação. Mudar qualquer um dos eixos inverterá a orientação, mas mudar ambos deixará a orientação inalterada.
Em três dimensões
Depois que os eixos x e y são especificados, eles determinam a linha ao longo da qual o eixo z deve ficar, mas há são duas orientações possíveis para esta linha. Os dois sistemas de coordenadas possíveis que resultam são chamados de 'destros' e 'canhoto'. A orientação padrão, onde o plano xy é horizontal e o eixo z aponta para cima (e o x- e o y O eixo forma um sistema de coordenadas bidimensional orientado positivamente no plano xy se observado de acima do plano xy) é chamado de destro ou positivo.
O nome deriva da regra da mão direita. Se o dedo indicador da mão direita estiver apontado para a frente, o dedo médio dobrado para dentro em ângulo reto com ele e o polegar colocado em ângulo reto com ambos, os três dedos indicam a orientação relativa do x-, y-, e z-eixos em um sistema destro. O polegar indica o eixo x, o dedo indicador o eixo y e o dedo médio o eixo z. Inversamente, se o mesmo for feito com a mão esquerda, o resultado será um sistema canhoto.
A Figura 7 mostra um sistema de coordenadas para a esquerda e para a direita. Como um objeto tridimensional é representado na tela bidimensional, o resultado é distorção e ambigüidade. O eixo que aponta para baixo (e para a direita) também aponta na direção do observador, enquanto o eixo "meio" aponta para longe do observador. O círculo vermelho é paralelo ao plano horizontal xy e indica a rotação do eixo x para o y -axis (em ambos os casos). Portanto, a seta vermelha passa na frente do eixo z.
A Figura 8 é outra tentativa de representar um sistema de coordenadas de mão direita. Novamente, há uma ambigüidade causada pela projeção do sistema de coordenadas tridimensional no plano. Muitos observadores veem a Figura 8 como "inclinando-se para dentro e para fora" entre um cubo convexo e um "canto" côncavo. Isso corresponde às duas orientações possíveis do espaço. Vendo a figura como convexa dá um sistema de coordenadas canhoto. Assim, o "correto" Uma maneira de ver a Figura 8 é imaginar o eixo x apontando na direção do observador e, assim, vendo um canto côncavo.
Representando um vetor na base padrão
Um ponto no espaço em um sistema de coordenadas cartesianas também pode ser representado por um vetor de posição, que pode ser pensado como uma seta apontando da origem do sistema de coordenadas para o ponto. Se as coordenadas representam posições espaciais (deslocamentos), é comum representar o vetor da origem ao ponto de interesse como R- Sim.. Em duas dimensões, o vetor da origem ao ponto com coordenadas cartesianas (x, y) pode ser escrito como:
Onde? Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(10)(i) {\0end{pmatrix}}} e JJ= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(01){displaystyle mathbf {j} ={begin{pmatrix}0\1end{pmatrix}}} são vetores unitários na direção do x- eixo e Sim.-axis respectivamente, geralmente referido como o base padrão (em algumas áreas de aplicação estes também podem ser referidos como versors). Da mesma forma, em três dimensões, o vetor da origem ao ponto com coordenadas cartesianas (x,Sim.,zangão.)(x,y,z)} pode ser escrito como:
Onde? Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(100),(i) ={begin{pmatrix}1end{pmatrix}},} JJ= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(010),{displaystyle mathbf {j} ={begin{pmatrix}0\\0end{pmatrix}},} e k= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(001).{displaystyle mathbf {k} ={begin{pmatrix}0\\1end{pmatrix}}.}
Não existe uma interpretação natural da multiplicação de vetores para obter outro vetor que funcione em todas as dimensões, no entanto, existe uma maneira de usar números complexos para fornecer tal multiplicação. Em um plano cartesiano bidimensional, identifique o ponto com as coordenadas (x, y) com o número complexo z = x + iy. Aqui, i é a unidade imaginária e é identificada com o ponto com as coordenadas (0, 1), então não é o vetor unitário na direção do eixo x. Como os números complexos podem ser multiplicados dando outro número complexo, essa identificação fornece um meio de "multiplicar" vetores. Em um espaço cartesiano tridimensional, uma identificação semelhante pode ser feita com um subconjunto dos quaternions.
Aplicativos
As coordenadas cartesianas são uma abstração que tem uma infinidade de aplicações possíveis no mundo real. No entanto, três etapas construtivas estão envolvidas na sobreposição de coordenadas em uma aplicação de problema.
- As unidades de distância devem ser decididas definindo o tamanho espacial representado pelos números utilizados como coordenadas.
- Uma origem deve ser atribuída a uma localização espacial específica ou marco, e
- a orientação dos eixos deve ser definida usando cues direcionais disponíveis para todos, exceto um eixo.
Considere como exemplo a sobreposição de coordenadas cartesianas 3D sobre todos os pontos da Terra (ou seja, 3D geoespacial). Quilômetros são uma boa escolha de unidades, já que a definição original do quilômetro era geoespacial, com 10.000 km igualando a distância da superfície do equador ao Pólo Norte. Com base na simetria, o centro gravitacional da Terra sugere um posicionamento natural da origem (que pode ser detectado pelas órbitas dos satélites). O eixo de rotação da Terra fornece uma orientação natural para os eixos X, Y e Z, fortemente associado ao "para cima vs. para baixo", então Z positivo pode adotar a direção do geocentro para o Pólo Norte. Uma localização no equador é necessária para definir o eixo X, e o meridiano principal se destaca como uma orientação de referência, então o eixo X assume a orientação do geocentro para 0 graus longitude, 0 graus de latitude. Observe que com três dimensões e orientações de dois eixos perpendiculares fixados para X e Z, o eixo Y é determinado pelas duas primeiras opções. Para obedecer à regra da mão direita, o eixo Y deve apontar do geocentro para 90 graus longitude, 0 graus latitude. De uma longitude de -73.985656 graus, uma latitude 40.748433 graus e raio da Terra de 40.000/2π km, e transformando de coordenadas esféricas em cartesianas, pode-se estimar as coordenadas geocêntricas do Empire State Building, (x, y, z) = (1.330,53 km, 4.635,75 km, 4.155,46 km). A navegação GPS depende dessas coordenadas geocêntricas.
Em projetos de engenharia, o acordo sobre a definição de coordenadas é uma base crucial. Não se pode presumir que as coordenadas venham predefinidas para uma nova aplicação, portanto, o conhecimento de como erguer um sistema de coordenadas onde anteriormente não havia tal sistema de coordenadas é essencial para aplicar a estratégia de René Descartes. pensamento.
Enquanto as aplicações espaciais empregam unidades idênticas ao longo de todos os eixos, em aplicações comerciais e científicas, cada eixo pode ter diferentes unidades de medida associadas a ele (como quilogramas, segundos, libras, etc.). Embora os espaços de quatro e mais dimensões sejam difíceis de visualizar, a álgebra das coordenadas cartesianas pode ser estendida com relativa facilidade para quatro ou mais variáveis, de modo que certos cálculos envolvendo muitas variáveis podem ser feitos. (Esse tipo de extensão algébrica é o que é usado para definir a geometria de espaços de dimensões superiores.) Por outro lado, muitas vezes é útil usar a geometria de coordenadas cartesianas em duas ou três dimensões para visualizar relações algébricas entre duas ou três de muitas não -variáveis espaciais.
O gráfico de uma função ou relação é o conjunto de todos os pontos que satisfazem essa função ou relação. Para uma função de uma variável, f, o conjunto de todos os pontos (x, y), onde y = f(x) é o gráfico da função f. Para uma função g de duas variáveis, o conjunto de todos os pontos (x, y, z), onde z = g(x, y) é o gráfico da função g. Um esboço do gráfico de tal função ou relação consistiria em todas as partes salientes da função ou relação que incluiriam seus extremos relativos, sua concavidade e pontos de inflexão, quaisquer pontos de descontinuidade e seu comportamento final. Todos esses termos são mais bem definidos em cálculo. Esses gráficos são úteis em cálculo para entender a natureza e o comportamento de uma função ou relação.
Contenido relacionado
Transformada discreta de Fourier
Eliminação bicondicional
Distribuição binomial