Régua de cálculo

A régua de cálculo (também conhecida coloquialmente nos Estados Unidos como slipstick) é uma calculadora mecânica (um dos computadores analógicos mais simples) operada manualmente deslizando dois réguas para realizar multiplicação e divisão principalmente e, possivelmente, expoentes, raízes, logaritmos e trigonometria. Normalmente não é projetado para adição ou subtração, o que geralmente é realizado usando outros métodos, como um ábaco. A precisão máxima para réguas de cálculo lineares padrão é de cerca de três dígitos decimais significativos, enquanto a notação científica é usada para controlar a ordem de grandeza dos resultados.

As réguas de cálculo existem em diversos estilos e geralmente aparecem em formato linear, circular ou cilíndrico, com escalas de réguas de cálculo inscritas com marcações graduadas padronizadas. As réguas de cálculo fabricadas para áreas especializadas, como aviação ou finanças, normalmente apresentam escalas adicionais que auxiliam em cálculos especializados específicos dessas áreas. A régua de cálculo está intimamente relacionada aos nomogramas usados para cálculos específicos de aplicativos. Embora semelhante em nome e aparência a uma régua padrão, a régua de cálculo não se destina a ser usada para medir comprimento ou desenhar linhas retas.

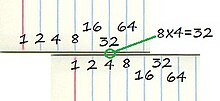
Na sua forma mais simples, cada número a ser multiplicado é representado por um comprimento em um par de réguas paralelas que podem deslizar uma sobre a outra. Como cada uma das réguas possui uma escala logarítmica, é possível alinhá-las para ler a soma dos números' logaritmos, que de acordo com a lei do logaritmo de um produto é igual ao produto dos dois números.

O matemático e clérigo inglês Reverendo William Oughtred e outros desenvolveram a régua de cálculo no século XVII com base no trabalho emergente sobre logaritmos de John Napier. Antes do advento da calculadora científica de bolso, ela era a ferramenta de cálculo mais usada em ciência e engenharia. A facilidade de uso, a pronta disponibilidade e o baixo custo da régua de cálculo fizeram com que seu uso continuasse a crescer durante as décadas de 1950 e 1960, mesmo com a introdução gradual dos computadores eletrônicos. A introdução da calculadora científica eletrônica portátil por volta de 1974 tornou as réguas de cálculo em grande parte obsoletas e a maioria dos fornecedores abandonou o negócio.

Conceitos básicos

Em sua forma mais básica, a régua de cálculo usa duas escalas logarítmicas para realizar multiplicações e divisões rápidas de números. Essas operações comuns podem ser demoradas e sujeitas a erros quando feitas no papel. Réguas de cálculo mais elaboradas podem realizar outros cálculos, como raízes quadradas, exponenciais, logaritmos e funções trigonométricas.

As escalas podem ser agrupadas em décadas, que são números que variam de 1 a 10 (ou seja, 10ⁿ a 10^{n+ 1}). Assim, as escalas C e D de uma década variam de 1 a 10 em toda a extensão da régua de cálculo, enquanto as escalas A e B de duas décadas variam de 1 a 100 em toda a extensão da régua de cálculo.

Em geral, os cálculos matemáticos são realizados alinhando uma marca na faixa central deslizante com uma marca em uma das faixas fixas e, em seguida, observando as posições relativas de outras marcas nas faixas. Os números alinhados com as marcas fornecem o valor aproximado do produto, quociente ou outro resultado calculado.

O usuário determina a localização do ponto decimal no resultado, com base em estimativa mental. A notação científica é usada para rastrear o ponto decimal em cálculos mais formais. As etapas de adição e subtração em um cálculo geralmente são feitas mentalmente ou no papel, e não na régua de cálculo.

A maioria das regras de cálculo consiste em três partes:

• Quadro ou base – duas tiras lineares do mesmo comprimento mantidas paralelas com uma lacuna entre.
• Slide – uma faixa central intertratada com o quadro que pode mover-se longitudinalmente em relação ao quadro.
• Corredor ou vidro – uma peça deslizante exterior com uma linha de cabelo, também conhecida como "cursor".

Algumas réguas de cálculo (modelos "duplex") possuem escalas em ambos os lados da régua e da tira deslizante, outras em um lado das tiras externas e em ambos os lados da tira deslizante (que geralmente pode ser puxada para fora, virados e reinseridos por conveniência), outros ainda apenas de um lado (regras "simplex"). Um cursor deslizante com uma linha de alinhamento vertical é usado para encontrar pontos correspondentes em escalas que não são adjacentes entre si ou, em modelos duplex, estão do outro lado da régua. O cursor também pode registrar um resultado intermediário em qualquer uma das escalas.

Operação

Um logaritmo transforma as operações de multiplicação e divisão para adição e subtração de acordo com as regras ${displaystyle log(xy)=log(x)+log(y)}$ e ${displaystyle log(x/y)=log(x)-log(y)}$. Movendo a escala superior para a direita por uma distância ${displaystyle log(x)}$, combinando o início da escala superior com a etiqueta $Não.$ na parte inferior, alinha cada número $- Sim.$, em posição ${displaystyle log(y)}$ na escala superior, com o número em posição ${displaystyle log(x)+log(y)}$ na escala inferior. Porque... ${displaystyle log(x)+log(y)=log(xy)}$, esta posição na escala inferior dá $Não.$, o produto de $Não.$ e $- Sim.$.

Multiplicação

Para multiplicar 3×2, o 1 na escala superior é movido para o 2 na escala inferior. A resposta, 6, é lida na escala inferior, onde 3 está na escala superior.

Para multiplicar 7×2, o 1 na escala superior é movido para o 2 na escala inferior. A resposta, 14, é lida na escala inferior, onde 7 está na escala superior. Como o 7 está acima do segundo conjunto de números, o resultado deve ser multiplicado por 10. Assim, mesmo que a resposta seja diretamente 1,4, a resposta correta é 1,4×10 = 14.

Para multiplicar 88×20, o 1 na escala superior é movido para o 2 na escala inferior. Como 2 representa 20 todos os números nessa escala são multiplicados por 10. Assim, qualquer resposta no segundo conjunto de números é multiplicada por 100. Como 8,8 na escala superior representa 88, a resposta deve ser adicionalmente multiplicada por 10< /span>. A resposta é diretamente 1,76. Multiplique por 100 e depois por 10 para obter a resposta real: 1.760.

Em geral, o 1 no topo é movido para um fator na parte inferior, e a resposta é lida na parte inferior, onde o outro fator está no topo. Isso funciona porque as distâncias da marca 1 são proporcionais aos logaritmos dos valores marcados.

Divisão

A ilustração abaixo demonstra o cálculo de 5,5/2. O 2 na escala superior é colocado sobre o 5,5 na escala inferior. O 1 na escala superior está acima do quociente, 2,75. Existe mais de um método para fazer divisão, e o método apresentado aqui tem a vantagem de que o resultado final não pode ficar fora da escala, pois é possível escolher usar o 1 em qualquer extremidade.

Com cálculos mais complexos envolvendo múltiplos fatores no numerador e no denominador de uma expressão, o movimento das escalas pode ser minimizado alternando divisões e multiplicações. Assim 5,5×3/< /span>2 seria calculado como 5,5/2×3 e o resultado, 8.25, pode ser lido abaixo do 3 na escala superior da figura acima, sem a necessidade de registre o resultado intermediário para 5.5 /2.

Outras operações

Além das escalas logarítmicas, algumas réguas de cálculo possuem outras funções matemáticas codificadas em outras escalas auxiliares. Os mais populares são trigonométricos, geralmente seno e tangente, logaritmo comum (log10) (para obter o logaritmo de um valor em uma escala multiplicadora), natural escalas logarítmicas (ln) e exponenciais (e^x). Algumas regras incluem uma escala pitagórica ("P") para resolver triângulos. Outros apresentam escalas para cálculo de funções hiperbólicas. Nas regras lineares, as escalas e sua rotulagem são altamente padronizadas, com a variação geralmente ocorrendo apenas em termos de quais escalas são incluídas e em que ordem:

A, B	escalas logarítmicas de duas décadas, duas seções cada uma das quais é metade do comprimento das escalas C e D, usado para encontrar raízes quadradas e quadrados de números
C, D	escalas logarítmicas únicas, seções únicas do mesmo comprimento, usadas em conjunto para multiplicação e divisão, e geralmente uma delas é combinada com outra escala para outros cálculos
KK	escala logarítmica de três décadas, três seções cada uma das quais é um terço o comprimento das escalas C e D, usado para encontrar raízes cubo e cubos de números
CF, DF	Versões "dobradas" das escalas C e D que começam de π em vez da unidade; estas são convenientes em dois casos. Primeiro quando o usuário adivinha que um produto será próximo de 10 e não tem certeza se será ligeiramente menos ou ligeiramente mais de 10, as escalas dobradas evitar a possibilidade de sair da escala. Em segundo lugar, fazendo o início π em vez da raiz quadrada de 10, multiplicando-se ou dividindo-se por π (como é comum em fórmulas de ciência e engenharia) é simplificado.
CI, DI, CIF, DIF	escalas "invertidas", correndo da direita para a esquerda, usadas para simplificar 1/x passos
S	usado para encontrar pecados e cossenos na escala C (ou D)
T, T1, T2	usado para encontrar tangentes e cotangentes nas escalas C e CI (ou D e DI)
R1, R2	escalas de raiz quadradas – definir o cursor para qualquer valor $Não.$ em R1 ou R2, encontrar $- Sim.$ (área de um círculo de raio $Não.$) sob o cursor na escala DF
ST, SRT	usado para pecados e tangentes de pequenos ângulos e conversão de grau-radian
Sh, Sh1, Sh2	usado para encontrar pecados hiperbólicos na escala C (ou D)
Ch	usado para encontrar cosinas hiperbólicas na escala C (ou D)
O quê?	usado para encontrar tangentes hiperbólicos na escala C (ou D)
L	uma escala linear, usada para adição, subtração e (juntamente com as escalas C e D) para encontrar logaritmos base-10 e poderes de 10.
LL0N (ou LL/N) e LLN	o log-log dobrado ${displaystyle e^{-x}}$ e ${displaystyle e^{x}}$ escalas, para trabalhar com logaritmos de qualquer base, e expoentes arbitrários. 4, 6 ou 8 escalas deste tipo são comumente vistas.
Ln	uma escala linear, usada junto com as escalas C e D para encontrar natural (base $Não.$) logaritmos e ${displaystyle e^{x}}$

As escalas na frente e na parte de trás de uma regra de slides Keuffel e Esser (K&E) 4181-3

A régua de cálculo binária fabricada por Gilson em 1931 executava uma função de adição e subtração limitada a frações.

Raízes e poderes

Existem escalas mono-decade (C e D), dupla-decade (A e B), e triple-decade (K). Para calcular ${displaystyle x^{2}}$, por exemplo, localizar x na escala D e ler seu quadrado na escala A. Inverter este processo permite que as raízes quadradas sejam encontradas, e da mesma forma para os poderes 3, 1/3, 2/3 e 3/2. Cuidados devem ser tomados quando a base, x, é encontrada em mais de um lugar em sua escala. Por exemplo, há dois noves na escala A; para encontrar a raiz quadrada de nove, use o primeiro; o segundo dá a raiz quadrada de 90.

Para ${displaystyle x^{y}}$ problemas, use as escalas LL. Quando várias escalas LL estão presentes, use aquela com x sobre ele. Primeiro, alinhe a esquerda 1 na escala C com x na escala LL. Então, encontrar Sim. na escala C e descer para a escala LL com x sobre ele. Essa escala indicará a resposta. Se Sim. está fora da escala, localizar ${displaystyle x^{y/2}}$ e cortá-lo usando as escalas A e B como descrito acima. Alternativamente, use o mais certo 1 na escala C e leia a resposta da próxima escala de LL superior. Por exemplo, alinhando o mais certo 1 na escala C com 2 na escala LL2, 3 nas linhas de escala C até 8 na escala LL3.

Para extrair uma raiz cúbica usando uma régua de cálculo apenas com escalas C/D e A/B, alinhe 1 no cursor B com o número base na escala A (tomando cuidado, como sempre, para distinguir entre as metades inferior e superior da escala A). Deslize o slide até que o número na escala D que está contra 1 no cursor C seja igual ao número no cursor B que está contra o número base na escala A. (Exemplos: A 8, B 2, C 1, D 2; A 27, B 3, C 1, D 3.)

Raízes de equações quadráticas

Equações quadráticas da forma ${displaystyle ax^{2}+bx+c=0}$ pode ser resolvido pela primeira vez reduzindo a equação para o formulário $Não. x^{2}-px+q=0}$ (onde) $Não. - O quê?$ e $Não. - Sim.$), e então alinhar o índice ("1") da escala C ao valor $Não.$ na escala D. O cursor é então movido ao longo da regra até que uma posição é encontrada onde os números nas escalas CI e D adicionam até $Não.$. Estes dois valores são as raízes da equação.

Trigonometria

As escalas S, T e ST são usadas para funções trigonométricas e múltiplos de funções trigonométricas, para ângulos em graus.

Para ângulos de cerca de 5,7 até 90 graus, os pecados são encontrados comparando a escala S com escala C (ou D). (Em muitas regras de corpo fechado, a escala S se relaciona com as escalas A e B em vez e abrange ângulos de cerca de 0,57 até 90 graus; o que se segue deve ser ajustado apropriadamente.) A escala S tem um segundo conjunto de ângulos (às vezes em uma cor diferente), que funcionam na direção oposta, e são usados para cossenos. Os tangentes são encontrados comparando a escala T com a escala C (ou D) para ângulos inferiores a 45 graus. Para ângulos superiores a 45 graus a escala CI é usada. Formas comuns como $- Sim.$ pode ser lido diretamente de x na escala S para o resultado na escala D, quando o índice de escala C é definido emk. Para ângulos abaixo de 5,7 graus, seios, tangentes e radianos são aproximadamente iguais, e são encontrados na escala ST ou SRT (sinos, radianos e tangentes), ou simplesmente divididos por 57,3 graus / rádio. Funções trigonométricas inversas são encontradas revertendo o processo.

Muitas réguas de cálculo têm escalas S, T e ST marcadas com graus e minutos (por exemplo, alguns modelos Keuffel e Esser (modelos Doric duplex 5", por exemplo), modelos mais recentes de regras do tipo Teledyne-Post Mannheim). Os chamados modelos decitrig usam frações decimais de graus.

Logaritmos e exponenciais

Logaritmos e exponenciais de base 10 são encontrados usando a escala L, que é linear. Algumas réguas de cálculo têm uma escala Ln, que é para base e. Logaritmos para qualquer outra base podem ser calculados invertendo o procedimento para calcular potências de um número. Por exemplo, os valores log2 podem ser determinados alinhando o 1 mais à esquerda ou o mais à direita na escala C com 2 na escala LL2, encontrando o número cujo logaritmo deve ser calculado na escala LL correspondente e lendo o valor log2 na escala C. escala.

Adição e subtração

A adição e a subtração normalmente não são realizadas em réguas de cálculo, mas são possíveis usando uma das duas técnicas a seguir:

1. Convertendo adição e subtração à divisão (necessário para o C e D ou escalas comparáveis):
   • Explora a identidade de que o quociente de duas variáveis mais (ou menos) uma vez o divisor é igual à sua soma (ou diferença):
     $${displaystyle {begin{aligned}left({frac {x}{y}}+1right)y&=x+y,{text{ (addition)}},\left({frac {x}{y}}-1right)y&=x-y,{text{ (subtraction)}}.end{aligned}}}$$

     
   • Isto é semelhante à técnica de adição / subtração usada para circuitos eletrônicos de alta velocidade com um sistema de número logarítmico em aplicações de computador especializadas, como o supercomputador Gravity Pipe (GRAPE) e modelos Markov ocultos.
2. Usando uma escala linear L (disponível em alguns modelos):
   • Depois de deslizar o cursor direito (para adição) ou esquerda (para subtração) e retornar o slide para 0, o resultado pode ser lido.

Generalizações

Usando (quase) qualquer escala estritamente monotônica, outros cálculos também podem ser feitos com um movimento. Por exemplo, escalas recíprocas podem ser usadas para a igualdade ${displaystyle {frac {1}{x}}+{frac Não. Não.$(calculando resistências paralelas, média harmônica, etc) e escalas quadráticas podem ser usadas para resolver $Não. x^{2}+y^{2}=z^{2}}$.

Projeto físico

Regras lineares padrão

A largura da régua de cálculo é cotada em termos da largura nominal das escalas. Escalas nas escalas mais comuns de "10 polegadas" os modelos têm, na verdade, 25 cm, pois foram feitos de acordo com padrões métricos, embora algumas regras ofereçam escalas ligeiramente estendidas para simplificar a manipulação quando um resultado transborda. As réguas de bolso normalmente têm 12 cm (5 polegadas). Modelos com alguns metros de largura foram feitos para serem pendurados nas salas de aula para fins didáticos.

Normalmente, as divisões marcam uma escala com precisão de dois algarismos significativos e o usuário estima o terceiro algarismo. Algumas réguas de cálculo de última geração possuem cursores ampliadores que facilitam a visualização das marcações. Esses cursores podem efetivamente dobrar a precisão das leituras, permitindo que uma régua de cálculo de 10 polegadas sirva tão bem quanto um modelo de 20 polegadas.

Várias outras conveniências foram desenvolvidas. As escalas trigonométricas às vezes têm rótulos duplos, em preto e vermelho, com ângulos complementares, as chamadas escalas "Darmstadt" estilo. As réguas de cálculo duplex geralmente duplicam algumas das escalas no verso. As escalas são frequentemente "divididas" para obter maior precisão.

Láguas de cálculo circulares

As réguas de cálculo circulares vêm em dois tipos básicos, uma com dois cursores e outra com um prato livre e um cursor. As versões de cursor duplo realizam multiplicação e divisão mantendo um ângulo constante entre os cursores à medida que são girados em torno do mostrador. A versão de cursor único funciona mais como a régua de cálculo padrão por meio do alinhamento apropriado das escalas.

A vantagem básica de uma régua de cálculo circular é que a dimensão mais larga da ferramenta foi reduzida por um fator de cerca de 3 (ou seja, por π). Por exemplo, uma circular de 10 cm teria uma precisão máxima aproximadamente igual a uma régua de cálculo comum de 31,4 cm. As réguas de cálculo circulares também eliminam erros 'fora de escala'. cálculos, porque as escalas foram projetadas para "envolver"; eles nunca precisam ser reorientados quando os resultados estão próximos de 1,0 – a regra está sempre em escala. No entanto, para escalas não cíclicas e não espirais, como S, T e LL's, a largura da escala é reduzida para abrir espaço para as margens finais.

As réguas de cálculo circulares são mecanicamente mais robustas e com movimentos mais suaves, mas a precisão do alinhamento da escala é sensível à centralização de um pivô central; um minuto de 0,1 mm (0,0039 pol.) fora do centro do pivô pode resultar em um erro de alinhamento de 0,2 mm (0,0079 pol.) no pior caso. O pivô evita arranhões na face e nos cursores. As escalas de maior precisão são colocadas nos anéis externos. Em vez de 'dividir' escalas, as regras circulares de ponta usam escalas espirais para operações mais complexas, como escalas log-of-log. Uma régua circular premium de oito polegadas tinha uma escala log-log em espiral de 50 polegadas. Por volta de 1970, um modelo barato de BC Boykin (Modelo 510) apresentava 20 escalas, incluindo CD (multiplicação) de 50 polegadas e escalas logarítmicas. O RotaRule apresentava um freio de fricção para o cursor.

As principais desvantagens das réguas de cálculo circulares são a dificuldade em localizar figuras ao longo de um prato e o número limitado de escalas. Outra desvantagem das réguas de cálculo circulares é que as escalas menos importantes estão mais próximas do centro e têm precisões mais baixas. A maioria dos alunos aprendeu o uso da régua de cálculo nas réguas de cálculo lineares e não encontrou motivo para mudar.

Uma régua de cálculo ainda em uso diário em todo o mundo é a E6B. Esta é uma régua de cálculo circular criada pela primeira vez na década de 1930 para pilotos de aeronaves para ajudar no cálculo morto. Com a ajuda de escalas impressas na estrutura, ele também ajuda em tarefas diversas, como conversão de valores de tempo, distância, velocidade e temperatura, erros de bússola e cálculo do uso de combustível. A chamada "roda de oração" ainda está disponível em lojas de aviação e continua amplamente utilizado. Embora o GPS tenha reduzido o uso de cálculo morto para navegação aérea e as calculadoras portáteis tenham assumido muitas de suas funções, o E6B continua amplamente utilizado como dispositivo primário ou de backup e a maioria das escolas de aviação exige que seus alunos tenham algum grau de proficiência em seu uso.

Rodas de proporção são réguas de cálculo circulares simples usadas em design gráfico para calcular proporções. Alinhar os valores de tamanho original e desejado nas rodas internas e externas exibirá sua proporção como uma porcentagem em uma pequena janela. Embora não sejam tão comuns desde o advento do layout computadorizado, eles ainda são feitos e usados.

Em 1952, a empresa relojoeira suíça Breitling lançou um relógio de pulso para piloto com uma régua de cálculo circular integrada especializada em cálculos de voo: o Breitling Navitimer. A regra circular do Navitimer, referida pela Breitling como um “computador de navegação”, apresentava funções de velocidade no ar, taxa/tempo de subida/descida, tempo de voo, distância e consumo de combustível, bem como quilometragem – milha náutica e funções de conversão de quantidade de combustível galão-litro.

• 

  Uma regra de slide circular simples, feita pela Concise Co., Ltd., Tóquio, Japão, com apenas escalas inversas, quadradas e cúbicos. No verso é uma lista útil de 38 fatores de conversão métrica/imperial.

• 

  Uma regra de corrediça circular russa construída como um relógio de bolso que funciona como regra de slide de cursor único desde que as duas agulhas são agrupadas

• 

  Uma regra de deslizamento de duas escalas construída em um anel

• 

  Regra de slide circular Pickett com dois cursores. (4,25 em 10,9 cm de largura) O reverso tem escala adicional e um cursor.

• 

  Breitling Navitimer relógio de pulso com regra de slide circular

• 

  O lado frontal de um Boykin RotaRule Modelo 510

• 

  O lado traseiro de um Boykin RotaRule Modelo 510

• 

  Calculadora de bolso Sperry 4016

Láguas de cálculo cilíndricas

Existem dois tipos principais de réguas de cálculo cilíndricas: aquelas com escalas helicoidais, como a calculadora Fuller, a Otis King e a régua de cálculo Bygrave, e aquelas com barras, como a Thacher e alguns modelos Loga. Em qualquer dos casos, a vantagem é uma escala muito mais longa e, portanto, uma precisão potencialmente maior, do que a proporcionada por uma regra recta ou circular.

• 

  calculadora completa, 1928

• 

  Modelo de Rei Otis KK

• 

  Regra geral da lâmina

• 

  Regra de slide de Thacher, por volta de 1890

Materiais

Tradicionalmente, as réguas de cálculo eram feitas de madeira dura, como mogno ou buxo, com cursores de vidro e metal. Pelo menos um instrumento de alta precisão era feito de aço.

Em 1895, uma empresa japonesa, Hemmi, começou a fabricar réguas de cálculo com bambu revestido de celulóide, que tinha as vantagens de ser dimensionalmente estável, forte e naturalmente autolubrificante. Estas réguas de bambu foram introduzidas na Suécia em setembro de 1933, e provavelmente apenas um pouco antes na Alemanha.

As balanças também eram feitas de celulóide ou outros polímeros, ou impressas em alumínio. Os cursores posteriores foram moldados em acrílico ou policarbonato, às vezes com superfícies de rolamento de Teflon.

Todas as réguas de cálculo premium tinham números e escalas gravados profundamente e depois preenchidos com tinta ou outra resina. Réguas de cálculo pintadas ou impressas foram consideradas inferiores, porque as marcações poderiam desgastar-se ou ser danificadas quimicamente. No entanto, a Pickett, uma empresa americana de réguas de cálculo, fabricava apenas réguas de escala impressas. As réguas de cálculo premium incluíam travas mecânicas inteligentes para que a régua não se desfizesse acidentalmente e amortecedores para proteger a balança e o cursor de esfregar no tampo das mesas.

Histórico

A régua de cálculo foi inventada por volta de 1620-1630, logo após a publicação do conceito de logaritmo por John Napier. Em 1620, Edmund Gunter, de Oxford, desenvolveu um dispositivo de cálculo com uma única escala logarítmica; com ferramentas de medição adicionais, poderia ser usado para multiplicar e dividir. Em c. 1622, William Oughtred, de Cambridge, combinou duas réguas portáteis de Gunter para criar um dispositivo que é reconhecidamente a régua de cálculo moderna. Oughtred se envolveu em uma controvérsia mordaz sobre prioridade, com seu ex-aluno Richard Delamain e as reivindicações anteriores de Wingate. As ideias de Oughtred só foram divulgadas nas publicações de seu aluno William Forster em 1632 e 1653.

Em 1677, Henry Coggeshall criou uma régua dobrável de 60 centímetros para medir madeira, chamada régua de cálculo Coggeshall, expandindo o uso da régua de cálculo além da investigação matemática.

Em 1722, Warner introduziu as escalas de duas e três décadas e, em 1755, Everard incluiu uma escala invertida; uma régua de cálculo contendo todas essas escalas é geralmente conhecida como "polifásica" regra.

Em 1815, Peter Mark Roget inventou a régua de cálculo log log, que incluía uma escala exibindo o logaritmo do logaritmo. Isso permitiu ao usuário realizar cálculos diretamente envolvendo raízes e expoentes. Isto foi especialmente útil para potências fracionárias.

Em 1821, Nathaniel Bowditch, descreveu no American Practical Navigator uma "regra de cálculo" que continha funções trigonométricas escalonadas na parte fixa e uma linha de log-senos e log-tans no controle deslizante usado para resolver problemas de navegação.

Em 1845, Paul Cameron, de Glasgow, introduziu uma régua de cálculo náutica capaz de responder a questões de navegação, incluindo a ascensão reta e a declinação do Sol e das estrelas principais.

Forma moderna

Uma forma mais moderna de régua de cálculo foi criada em 1859 pelo tenente de artilharia francês Amédée Mannheim, que teve a sorte de ter sua regra feita por uma empresa de reputação nacional e de sua adoção pela artilharia francesa. A regra de Mannheim teve duas modificações principais que a tornaram mais fácil de usar do que as réguas de cálculo de uso geral anteriores. Essas regras tinham quatro escalas básicas, A, B, C e D, e D era a única escala logarítmica de uma década; C teve duas décadas, assim como A e B. A maioria das operações foi feita nas escalas A e B; D foi usado apenas para encontrar quadrados e raízes quadradas.

Mannheim mudou a escala C para uma escala de uma década e realizou a maioria das operações com C e D em vez de A e B. Como as escalas C e D eram de uma década, elas podiam ser lidas com mais precisão, então a regra&# Os resultados da empresa poderiam ser mais precisos. A mudança também tornou mais fácil incluir quadrados e raízes quadradas como parte de um cálculo maior. A regra de Mannheim também tinha um cursor, ao contrário de quase todas as regras anteriores, de modo que qualquer uma das escalas poderia ser comparada com facilidade e precisão ao longo da largura da regra. A 'regra de Mannheim' tornou-se o arranjo padrão da régua de cálculo no final do século 19 e permaneceu um padrão comum durante toda a era da régua de cálculo.

O crescimento da profissão de engenheiro durante o final do século XIX impulsionou o uso generalizado de réguas de cálculo, começando na Europa e eventualmente se consolidando também nos Estados Unidos. A regra duplex foi inventada por William Cox em 1891 e produzida pela Keuffel and Esser Co.

Em 1881, o inventor americano Edwin Thacher introduziu sua regra cilíndrica, que tinha uma escala muito mais longa do que as regras lineares padrão e, portanto, podia calcular com maior precisão cerca de quatro a cinco dígitos significativos. No entanto, a regra de Thacher era bastante cara, além de não ser portátil, por isso era usada em números muito mais limitados do que as réguas de cálculo convencionais.

O trabalho astronômico também exigia cálculos precisos e, na Alemanha do século XIX, uma régua de cálculo de aço com cerca de dois metros de comprimento foi usada em um observatório. Ele tinha um microscópio acoplado, proporcionando precisão de seis casas decimais.

Na década de 1920, o romancista e engenheiro Nevil Shute Norway (ele chamou sua autobiografia de Slide Rule) foi o Calculador Chefe no projeto do dirigível britânico R100 para a Vickers Ltd. para cada quadro transversal foram necessários cálculos por um par de calculadoras (pessoas) usando as réguas de cálculo cilíndricas de Fuller durante dois ou três meses. A equação simultânea continha até sete quantidades desconhecidas, levava cerca de uma semana para ser resolvida e precisava ser repetida com uma seleção diferente de fios frouxos se a estimativa de qual dos oito fios radiais estava frouxo estivesse errada e um dos fios adivinhasse ser preguiçoso não era preguiçoso. Depois de meses de trabalho preenchendo talvez cinquenta folhas de papel almaço com cálculos “a verdade foi revelada (e) produziu uma satisfação quase equivalente a uma experiência religiosa”.

Ao longo das décadas de 1950 e 1960, a régua de cálculo foi o símbolo da profissão de engenheiro, da mesma forma que o estetoscópio é o símbolo da profissão médica.

Ráguas de cálculo da marca Pickett de alumínio foram transportadas nas missões espaciais do Projeto Apollo. O modelo N600-ES de propriedade de Buzz Aldrin que voou com ele para a Lua na Apollo 11 foi vendido em leilão em 2007. O modelo N600-ES levado na Apollo 13 em 1970 é propriedade do Museu Nacional do Ar e do Espaço.

Alguns estudantes de engenharia e engenheiros carregavam réguas de cálculo de dez polegadas em coldres de cinto, uma visão comum nos campi até meados da década de 1970. Até o advento da calculadora digital de bolso, os alunos também podiam manter uma régua de dez ou vinte polegadas para trabalhos de precisão em casa ou no escritório, enquanto carregavam consigo uma régua de cálculo de bolso de cinco polegadas.

Em 2004, os pesquisadores em educação David B. Sher e Dean C. Nataro conceberam um novo tipo de régua de cálculo baseada na prosthaphaeresis, um algoritmo para calcular produtos rapidamente que antecede os logaritmos. No entanto, tem havido pouco interesse prático em construir um além do protótipo inicial.

Calculadoras especializadas

As réguas de cálculo costumam ser especializadas em vários graus para seu campo de uso, como impostos especiais de consumo, cálculo de provas, engenharia, navegação, etc., e algumas réguas de cálculo são extremamente especializadas para aplicações muito restritas. Por exemplo, o John Rabone & O catálogo Sons 1892 lista uma 'Fita Métrica e Medidor de Gado', um dispositivo para estimar o peso de uma vaca a partir de suas medidas.

Havia muitas réguas de cálculo especializadas para aplicações fotográficas. Por exemplo, o actinógrafo de Hurter e Driffield era um dispositivo de buxo, latão e papelão com duas lâminas para estimar a exposição a partir da hora do dia, época do ano e latitude.

Ráguas de cálculo especializadas foram inventadas para diversas formas de engenharia, negócios e bancos. Muitas vezes tinham cálculos comuns expressos diretamente como escalas especiais, por exemplo, cálculos de empréstimos, quantidades ótimas de compra ou equações de engenharia específicas. Por exemplo, a empresa Fisher Controls distribuiu uma régua de cálculo personalizada adaptada para resolver as equações usadas para selecionar o tamanho adequado das válvulas de controle de fluxo industrial.

As réguas de cálculo do balão piloto foram usadas por meteorologistas em serviços meteorológicos para determinar as velocidades superiores do vento a partir de um balão piloto ascendente cheio de hidrogênio ou hélio.

A E6-B é uma régua de cálculo circular usada por pilotos e navegadores.

As réguas de cálculo circulares para estimar as datas de ovulação e fertilidade são conhecidas como calculadoras de roda.

Uma publicação do Departamento de Defesa de 1962 incluía de forma infame uma régua de cálculo circular de propósito especial para calcular efeitos de explosão, sobrepressão e exposição à radiação de um determinado rendimento de uma bomba atômica.

• 

  Um computador de aviação E6-B

• 

  John Rabone & Sons 1892 galho de gado

• 

  Atriz de Hurter e Driffield

• 

  Regra de corrediça criptográfica utilizada pelo Exército suíço entre 1914 e 1940

• 

  Adição fracionada rara

Recusar

A importância da régua de cálculo começou a diminuir à medida que os computadores eletrónicos, um recurso novo mas raro na década de 1950, tornaram-se mais amplamente disponíveis aos trabalhadores técnicos durante a década de 1960.

O primeiro passo para se afastar das réguas de cálculo foi a introdução de calculadoras científicas eletrônicas de mesa, relativamente baratas. Estes incluíam o LOCI-2 dos Laboratórios Wang, lançado em 1965, que usava logaritmos para multiplicação e divisão; e o Hewlett-Packard HP 9100A, lançado em 1968. Ambos eram programáveis e forneciam funções exponenciais e logarítmicas; o HP tinha funções trigonométricas (seno, cosseno e tangente) e também funções trigonométricas hiperbólicas. A HP utilizou o algoritmo CORDIC (computador digital de rotação de coordenadas), que permite o cálculo de funções trigonométricas usando apenas operações de deslocamento e adição. Este método facilitou o desenvolvimento de calculadoras científicas cada vez menores.

Tal como acontece com a computação mainframe, a disponibilidade destas máquinas de secretária não afetou significativamente a utilização omnipresente da régua de cálculo, até que calculadoras eletrónicas científicas portáteis e baratas se tornaram disponíveis em meados da década de 1970, altura em que declinou rapidamente. A calculadora científica Hewlett-Packard HP-35 de bolso foi o primeiro dispositivo portátil desse tipo, mas custou US$ 395 em 1972. Isso era justificável para alguns profissionais de engenharia, mas muito caro para a maioria dos estudantes.

Por volta de 1974, calculadoras científicas eletrônicas portáteis de baixo custo começaram a tornar as réguas de cálculo bastante obsoletas. Em 1975, calculadoras eletrônicas básicas de quatro funções podiam ser compradas por menos de US$ 50, e em 1976 a calculadora científica TI-30 era vendida por menos de US$ 25 (US$ 129 ajustados pela inflação).

1980 foi o último ano da competição da University Interscholastic League (UIL) no Texas para o uso de réguas de cálculo. O UIL foi originalmente organizado em 1910 para administrar eventos literários, mas também se tornou o órgão regulador dos eventos esportivos escolares.

Comparação com calculadoras digitais eletrônicas

Mesmo durante seu apogeu, as réguas de cálculo nunca agradaram o público em geral. Adição e subtração não são operações bem suportadas em réguas de cálculo e fazer um cálculo em uma régua de cálculo tende a ser mais lento do que em uma calculadora. Isso levou os engenheiros a usar equações matemáticas que favoreciam operações fáceis em uma régua de cálculo em vez de funções mais precisas, mas complexas; essas aproximações podem levar a imprecisões e erros. Por outro lado, a operação espacial e manual das réguas de cálculo cultiva no usuário uma intuição para relações numéricas e escala que muitas vezes falta às pessoas que usaram apenas calculadoras digitais. Uma régua de cálculo também exibirá todos os termos de um cálculo junto com o resultado, eliminando assim a incerteza sobre qual cálculo foi realmente executado. Assim, foi comparado com a notação polonesa reversa (RPN) implementada em calculadoras eletrônicas.

Uma régua de cálculo exige que o usuário calcule separadamente a ordem de grandeza da resposta para posicionar o ponto decimal nos resultados. Por exemplo, 1,5 × 30 (que é igual a 45) mostrará o mesmo resultado que 1500000 × 0,03 (que é igual a 45000). Este cálculo separado força o usuário a acompanhar a magnitude na memória de curto prazo (que é propensa a erros), fazer anotações (o que é complicado) ou raciocinar sobre isso em cada etapa (o que desvia a atenção dos outros requisitos de cálculo).

A precisão aritmética típica de uma régua de cálculo é de cerca de três dígitos significativos, em comparação com muitos dígitos nas calculadoras digitais. Como a ordem de magnitude ganha maior destaque ao usar uma régua de cálculo, os usuários são menos propensos a cometer erros de falsa precisão.

Ao realizar uma sequência de multiplicações ou divisões pelo mesmo número, a resposta muitas vezes pode ser determinada simplesmente olhando para a régua de cálculo, sem qualquer manipulação. Isto pode ser especialmente útil ao calcular percentagens (por exemplo, para resultados de testes) ou ao comparar preços (por exemplo, em dólares por quilograma). Vários cálculos de velocidade-tempo-distância podem ser realizados rapidamente com as mãos livres com uma régua de cálculo. Outras conversões lineares úteis, como libras em quilogramas, podem ser facilmente marcadas na régua e usadas diretamente nos cálculos.

Sendo totalmente mecânica, uma régua de cálculo não depende de eletricidade da rede ou de baterias. A imprecisão mecânica em réguas de cálculo mal construídas ou deformadas pelo calor ou pelo uso levará a erros.

Muitos marinheiros mantêm réguas de cálculo como backup para a navegação em caso de falha elétrica ou esgotamento da bateria em trechos de rota longos. As réguas de cálculo ainda são comumente usadas na aviação, especialmente para aviões menores. Eles estão sendo substituídos apenas por computadores de voo integrados, de uso especial e caros, e não por calculadoras de uso geral. A régua de cálculo circular E6B usada pelos pilotos está em produção contínua e permanece disponível em vários modelos. Alguns relógios de pulso projetados para uso na aviação ainda apresentam escalas de régua de cálculo para permitir cálculos rápidos. O Citizen Skyhawk AT e o Seiko Flightmaster SNA411 são dois exemplos notáveis.

Uso contemporâneo

Mesmo no século 21, algumas pessoas preferem uma régua de cálculo a uma calculadora eletrônica como um dispositivo de computação prático. Outros mantêm suas antigas regras de cálculo por nostalgia ou as colecionam como hobby.

Um modelo colecionável popular é o Keuffel & Esser Deci-Lon, uma régua de cálculo científica e de engenharia premium disponível em formato "normal" (Deci-Lon 10) e um "bolso" (Deci-Lon 5). Outro modelo americano premiado é a régua circular de oito polegadas (20 cm) da Scientific Instruments. Das regras europeias, os modelos topo de linha da Faber-Castell são os mais populares entre os colecionadores.

Embora muitas réguas de cálculo estejam circulando no mercado, amostras em boas condições tendem a ser caras. Muitas regras encontradas à venda em sites de leilões online estão danificadas ou faltam peças, e o vendedor pode não saber o suficiente para fornecer as informações relevantes. As peças de reposição são escassas, caras e geralmente disponíveis apenas para compra separada em colecionadores individuais. sites. As regras de Keuffel e Esser do período até cerca de 1950 são particularmente problemáticas, porque as extremidades dos cursores, feitas de celulóide, tendem a quebrar quimicamente com o tempo. Métodos de preservação de plástico podem ser usados para retardar a deterioração de algumas réguas de cálculo mais antigas, e a impressão 3D pode ser usada para recriar partes do cursor ausentes ou irremediavelmente quebradas.

Ainda existem algumas fontes para novas réguas de cálculo. A Concise Company of Tokyo, que começou como fabricante de réguas de cálculo circulares em julho de 1954, continua a fabricá-las e vendê-las até hoje. Em setembro de 2009, o varejista on-line ThinkGeek lançou sua própria marca de réguas de cálculo simples, descritas como “réplicas fiéis”; que foram "fabricados individualmente à mão". Eles não estavam mais disponíveis em 2012. Além disso, a Faber-Castell tinha uma série de réguas de cálculo em estoque, disponíveis para compra internacional em sua loja virtual, até meados de 2018. As rodas de proporção ainda são usadas em design gráfico.

Vários aplicativos simuladores de réguas de cálculo estão disponíveis para smartphones e tablets Android e iOS.

Ráguas de cálculo especializadas, como o E6B usado na aviação, e réguas de cálculo de artilharia usadas no lançamento de artilharia ainda são usadas, embora não mais rotineiramente. Estas regras são utilizadas como parte do processo de ensino e instrução, pois ao aprender a utilizá-las o aluno também aprende sobre os princípios por trás dos cálculos, também permite que o aluno seja capaz de utilizar estes instrumentos como reserva no caso de o moderno eletrônicos de uso geral falham.

Coleções

O Museu do MIT em Cambridge, Massachusetts, tem uma coleção de centenas de réguas de cálculo, nomogramas e calculadoras mecânicas. A coleção Keuffel and Esser Company, do fabricante de réguas de cálculo anteriormente localizado em Hoboken, Nova Jersey, foi doada ao MIT por volta de 2005, expandindo substancialmente o acervo existente. Itens selecionados da coleção geralmente ficam em exibição no museu.

O Museu Internacional de Réguas de Cálculo é considerado o “recurso mais extenso [do mundo] para todas as coisas relacionadas a réguas de cálculo e calculadoras logarítmicas”. A página da Web do museu inclui extensa literatura relativa às regras de cálculo em sua "Biblioteca de regras de cálculo" seção.