Reação nuclear em cadeia

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Quando uma reação nuclear causa mais

Uma possível reação em cadeia de fissão nuclear:
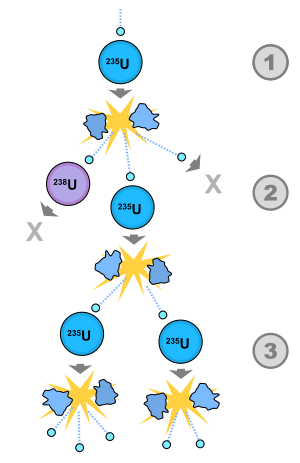
1) Um átomo de urânio-235 absorve um nêutron e fissões em dois (fragmentos de ficção), liberando três novos neutrões e uma grande quantidade de energia de ligação.
2) Um desses neutrões é absorvido por um átomo de urânio-238, e não continua a reação. Outro nêutron deixa o sistema sem ser absorvido. No entanto, um nêutron colide com um átomo de urânio-235, que então fissões e libera dois nêutrons e mais energia de ligação.
3) Ambos os neutrões colidem com átomos de urânio-235, cada um dos quais fissões e libera alguns neutrões, que podem então continuar a reação.

Na física nuclear, uma reação nuclear em cadeia ocorre quando uma única reação nuclear causa uma média de uma ou mais reações nucleares subsequentes, levando assim à possibilidade de uma série de autopropagação dessas reações. A reação nuclear específica pode ser a fissão de isótopos pesados (por exemplo, urânio-235, ²³⁵U). Uma reação nuclear em cadeia libera vários milhões de vezes mais energia por reação do que qualquer reação química.

História

As reações químicas em cadeia foram propostas pela primeira vez pelo químico alemão Max Bodenstein em 1913, e eram razoavelmente bem compreendidas antes que as reações nucleares em cadeia fossem propostas. Entendeu-se que as reações químicas em cadeia eram responsáveis por aumentar exponencialmente as taxas de reações, como as produzidas em explosões químicas.

O conceito de uma reação nuclear em cadeia foi supostamente formulado pela primeira vez pelo cientista húngaro Leó Szilárd em 12 de setembro de 1933. Szilárd naquela manhã estava lendo em um jornal de Londres sobre um experimento no qual prótons de um acelerador foram usados para dividir o lítio -7 em partículas alfa, e o fato de que quantidades muito maiores de energia foram produzidas pela reação do que o próton fornecido. Ernest Rutherford comentou no artigo que as ineficiências no processo impossibilitavam seu uso para geração de energia. No entanto, o nêutron havia sido descoberto por James Chadwick em 1932, pouco antes, como produto de uma reação nuclear. Szilárd, que havia se formado como engenheiro e físico, juntou os dois resultados experimentais nucleares em sua mente e percebeu que, se uma reação nuclear produzisse nêutrons, que então causassem outras reações nucleares semelhantes, o processo poderia ser uma cadeia nuclear autoperpetuante. -reação, produzindo espontaneamente novos isótopos e energia sem a necessidade de prótons ou acelerador. Szilárd, no entanto, não propôs a fissão como mecanismo para sua reação em cadeia, uma vez que a reação de fissão ainda não foi descoberta, ou mesmo suspeitada. Em vez disso, Szilárd propôs o uso de misturas de isótopos conhecidos mais leves que produziam nêutrons em grandes quantidades. Ele registrou uma patente para sua ideia de um reator nuclear simples no ano seguinte.

Em 1936, Szilárd tentou criar uma reação em cadeia usando berílio e índio, mas não teve sucesso. A fissão nuclear foi descoberta por Otto Hahn e Fritz Strassmann em dezembro de 1938 e explicada teoricamente em janeiro de 1939 por Lise Meitner e seu sobrinho Otto Robert Frisch. Em sua segunda publicação sobre fissão nuclear em fevereiro de 1939, Hahn e Strassmann usaram pela primeira vez o termo Uranspaltung (fissão de urânio) e previram a existência e liberação de nêutrons adicionais durante o processo de fissão, abrindo a possibilidade de uma reação nuclear em cadeia.

Alguns meses depois, Frédéric Joliot-Curie, H. Von Halban e L. Kowarski em Paris procuraram e descobriram a multiplicação de nêutrons no urânio, provando que uma reação nuclear em cadeia por esse mecanismo era realmente possível.

Em 4 de maio de 1939, Joliot-Curie, Halban e Kowarski registraram três patentes. Os dois primeiros descreviam a produção de energia a partir de uma reação nuclear em cadeia, o último chamado Perfectionnement aux charge explosivos foi a primeira patente para a bomba atômica e é registrada como patente nº 445686 pela Caisse nationale de Recherche Scientifique.

Paralelamente, Szilárd e Enrico Fermi em Nova York fizeram a mesma análise. Essa descoberta motivou a carta de Szilárd e assinada por Albert Einstein ao presidente Franklin D. Roosevelt, alertando sobre a possibilidade de a Alemanha nazista estar tentando construir uma bomba atômica.

Em 2 de dezembro de 1942, uma equipe liderada por Fermi (e incluindo Szilárd) produziu a primeira reação em cadeia nuclear autossustentável artificial com o reator experimental Chicago Pile-1 (CP-1) em uma quadra de raquetes abaixo das arquibancadas do Stagg Field da Universidade de Chicago. As experiências de Fermi na Universidade de Chicago faziam parte do Laboratório Metalúrgico de Arthur H. Compton do Projeto Manhattan; o laboratório foi posteriormente renomeado para Argonne National Laboratory e encarregado de conduzir pesquisas sobre o aproveitamento da fissão para energia nuclear.

Em 1956, Paul Kuroda, da Universidade de Arkansas, postulou que um reator de fissão natural pode ter existido. Como as reações nucleares em cadeia podem exigir apenas materiais naturais (como água e urânio, se o urânio tiver quantidades suficientes de ²³⁵U), é possível que essas reações em cadeia ocorram no passado distante, quando urânio- 235 eram maiores do que hoje, e onde havia a combinação certa de materiais dentro da crosta terrestre. ²³⁵
U compôs uma parcela maior de urânio na Terra no passado geológico devido à meia-vida diferente dos isótopos ²³⁵
U e ²³⁸
U, o o primeiro decaindo quase uma ordem de magnitude mais rápido que o último. A previsão de Kuroda foi verificada com a descoberta de evidências de reações em cadeia nucleares auto-sustentáveis naturais no passado em Oklo, no Gabão, em setembro de 1972. Para sustentar uma reação em cadeia de fissão nuclear nas atuais proporções isotópicas em urânio natural na Terra, a presença de um moderador de nêutrons como água pesada ou carbono de alta pureza (por exemplo, grafite) na ausência de venenos de nêutrons, que é ainda mais improvável de surgir por processos geológicos naturais do que as condições em Oklo há cerca de dois bilhões de anos.

Reação em cadeia de fissão

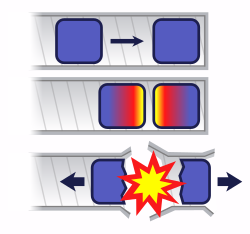
As reações em cadeia de fissão ocorrem devido a interações entre nêutrons e isótopos físseis (como ²³⁵U). A reação em cadeia requer tanto a liberação de nêutrons de isótopos físseis submetidos à fissão nuclear quanto a subsequente absorção de alguns desses nêutrons em isótopos físseis. Quando um átomo sofre fissão nuclear, alguns nêutrons (o número exato depende de fatores incontroláveis e não mensuráveis; o número esperado depende de vários fatores, geralmente entre 2,5 e 3,0) são ejetados da reação. Esses nêutrons livres irão interagir com o meio circundante e, se mais combustível físsil estiver presente, alguns podem ser absorvidos e causar mais fissões. Assim, o ciclo se repete para dar uma reação autossustentável.

As usinas de energia nuclear operam controlando com precisão a taxa na qual as reações nucleares ocorrem. As armas nucleares, por outro lado, são projetadas especificamente para produzir uma reação tão rápida e intensa que não pode ser controlada depois de iniciada. Quando projetada adequadamente, essa reação descontrolada levará a uma liberação explosiva de energia.

Combustível de fissão nuclear

As armas nucleares empregam combustível de alta qualidade e altamente enriquecido, excedendo o tamanho crítico e a geometria (massa crítica) necessários para obter uma reação explosiva em cadeia. O combustível para fins energéticos, como em um reator de fissão nuclear, é muito diferente, geralmente consistindo de um material de óxido de baixo enriquecimento (por exemplo, UO₂). Existem dois isótopos primários usados para reações de fissão dentro de reatores nucleares. O primeiro e mais comum é o urânio-235. Este é o isótopo físsil do urânio e representa aproximadamente 0,7% de todo o urânio natural. Devido à pequena quantidade de ²³⁵U existente, é considerada uma fonte de energia não renovável, apesar de ser encontrada em formações rochosas ao redor do mundo. O urânio-235 não pode ser usado como combustível em sua forma básica para produção de energia. Deve passar por um processo conhecido como refinamento para produzir o composto UO₂ ou dióxido de urânio. O dióxido de urânio é então prensado e transformado em pastilhas de cerâmica, que podem posteriormente ser colocadas em varetas de combustível. É quando o dióxido de urânio composto pode ser usado para produção de energia nuclear. O segundo isótopo mais comum usado na fissão nuclear é o plutônio-239. Isso se deve à sua capacidade de se tornar físsil com lenta interação de nêutrons. Este isótopo é formado dentro de reatores nucleares através da exposição de ²³⁸U aos nêutrons liberados durante a fissão. Como resultado da captura de nêutrons, é produzido urânio-239, que sofre dois decaimentos beta para se tornar plutônio-239. O plutônio já ocorreu como um elemento primordial na crosta terrestre, mas apenas vestígios permanecem, por isso é predominantemente sintético. Outro combustível proposto para reatores nucleares, que no entanto não desempenha nenhum papel comercial a partir de 2021, é o urânio-233, que é "criado" por captura de nêutrons e posterior decaimento beta do tório natural, que é quase 100% composto pelo isótopo tório-232. Isso é chamado de ciclo do combustível do tório.

Processo de enriquecimento

O isótopo físsil urânio-235 em sua concentração natural é impróprio para a grande maioria dos reatores nucleares. Para ser preparado para uso como combustível na produção de energia, ele deve ser enriquecido. O processo de enriquecimento não se aplica ao plutônio. O plutônio de grau reator é criado como um subproduto da interação de nêutrons entre dois diferentes isótopos de urânio. O primeiro passo para enriquecer urânio começa convertendo o óxido de urânio (criado através do processo de moagem de urânio) em uma forma gasosa. Este gás é conhecido como hexafluoreto de urânio, que é criado pela combinação de fluoreto de hidrogênio, gás flúor e óxido de urânio. O dióxido de urânio também está presente nesse processo e é enviado para ser usado em reatores que não requerem combustível enriquecido. O restante composto de hexafluoreto de urânio é drenado para fortes cilindros de metal onde se solidifica. O próximo passo é separar o hexafluoreto de urânio do U-235 empobrecido restante. Isso normalmente é feito com centrífugas que giram rápido o suficiente para permitir que a diferença de massa de 1% nos isótopos de urânio se separem. Um laser é então usado para enriquecer o composto de hexafluoreto. A etapa final envolve reconverter o composto agora enriquecido de volta em óxido de urânio, deixando o produto final: óxido de urânio enriquecido. Esta forma de UO₂ agora pode ser usada em reatores de fissão dentro de usinas de energia para produzir energia.

Produtos de reação de fissão

Quando um átomo físsil sofre fissão nuclear, ele se quebra em dois ou mais fragmentos de fissão. Além disso, vários nêutrons livres, raios gama e neutrinos são emitidos e uma grande quantidade de energia é liberada. A soma das massas restantes dos fragmentos de fissão e dos nêutrons ejetados é menor que a soma das massas restantes do átomo original e do nêutron incidente (é claro que os fragmentos de fissão não estão em repouso). A diferença de massa é contabilizada na liberação de energia de acordo com a equação E=Δmc2:

massa de energia liberada = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

{frac {E}{c^{2}}}=m_{text{original}}-m_{text{final}}

Devido ao valor extremamente grande da velocidade da luz, c, uma pequena diminuição na massa está associada a uma tremenda liberação de energia ativa (por exemplo, a energia cinética dos fragmentos de fissão). Essa energia (na forma de radiação e calor) transporta a massa que falta, quando sai do sistema de reação (a massa total, como a energia total, é sempre conservada). Enquanto as reações químicas típicas liberam energias da ordem de alguns eVs (por exemplo, a energia de ligação do elétron ao hidrogênio é de 13,6 eV), as reações de fissão nuclear geralmente liberam energias da ordem de centenas de milhões de eVs.

Duas reações típicas de fissão são mostradas abaixo com valores médios de energia liberada e número de nêutrons ejetados:

}}& {text{fission fragments}}+2.4{text{ neutrons}}+192.9{text{ MeV}}\{ce {^{239}Pu + neutron ->}}& {text{fission fragments}}+2.9{text{ neutrons}}+198.5{text{ MeV}}end{aligned}}}" xmlns="http://www.w3.org/1998/Math/MathML">U235+neutrões⟶ ⟶ ⟶ ⟶ fragmentos de fissão+2.neutrões+192.9Eu...Puxa.239+neutrões⟶ ⟶ ⟶ ⟶ fragmentos de fissão+2.9neutrões+19,5Eu...{displaystyle {begin{aligned}{ce {^{235}U + neutron ->}}& {text{fission fragments}}+2.4{text{ neutrões}}+192.9{text{ MeV}}textal {^{239}Pu + neutron ->}}& {text{fission fragments}}+2.9{text{ neutrões}}+198.5}}}}& {text{fission fragments}}+2.4{text{ neutrons}}+192.9{text{ MeV}}\{ce {^{239}Pu + neutron ->}}& {text{fission fragments}}+2.9{text{ neutrons}}+198.5{text{ MeV}}end{aligned}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/28af299dd44e6338b836aaab5f982d1dd86b67e8" style="vertical-align: -2.505ex; width:67.753ex; height:6.176ex;"/>

Observe que essas equações são para fissões causadas por nêutrons (térmicos) de movimento lento. A energia média liberada e o número de nêutrons ejetados é uma função da velocidade do nêutron incidente. Além disso, observe que essas equações excluem a energia dos neutrinos, pois essas partículas subatômicas são extremamente não reativas e, portanto, raramente depositam sua energia no sistema.

Calendários de reações nucleares em cadeia

Prompt de vida útil do nêutron

O tempo de vida imediato do nêutron, l, é o tempo médio entre a emissão de nêutrons e sua absorção no sistema ou sua fuga do sistema. Os nêutrons que ocorrem diretamente da fissão são chamados de "nêutrons imediatos", e os que são resultado do decaimento radioativo de fragmentos de fissão são chamados de "nêutrons retardados". O termo tempo de vida é usado porque a emissão de um nêutron é frequentemente considerada seu "nascimento", e a absorção subsequente é considerada sua "morte". Para reatores de fissão térmica (nêutrons lentos), o tempo de vida típico do nêutron imediato é da ordem de 10⁻⁴ segundos, e para reatores de fissão rápida, o tempo de vida imediato do nêutron é da ordem de 10⁻⁷ segundos. Esses tempos de vida extremamente curtos significam que em 1 segundo, 10.000 a 10.000.000 de nêutrons podem passar. O médio (também conhecido como adjunto não ponderado) tempo de vida do nêutron imediato leva em consideração todos os nêutrons imediatos, independentemente de sua importância no núcleo do reator; o tempo de vida imediato efetivo do nêutron (referido como o adjunto ponderado sobre espaço, energia e ângulo) refere-se a um nêutron com importância média.

Tempo médio de geração

O tempo médio de geração, Λ, é o tempo médio de uma emissão de nêutrons até uma captura que resulta em fissão. O tempo médio de geração é diferente do tempo de vida imediato do nêutron porque o tempo médio de geração inclui apenas absorções de nêutrons que levam a reações de fissão (não outras reações de absorção). Os dois tempos estão relacionados pela seguinte fórmula:

Lambda ={frac {l}{k}}

Nesta fórmula, k é o fator efetivo de multiplicação de nêutrons, descrito abaixo.

Fator efetivo de multiplicação de nêutrons

O fator de multiplicação efetiva de nêutrons da fórmula de seis fatores, k, é o número médio de nêutrons de uma fissão que causam outra fissão. Os nêutrons restantes são absorvidos em reações de não fissão ou deixam o sistema sem serem absorvidos. O valor de k determina como ocorre uma reação nuclear em cadeia:

k < 1 (subcriticalidade): O sistema não pode sustentar uma reação em cadeia, e qualquer início de uma reação em cadeia morre ao longo do tempo. Para cada fissão induzida no sistema, uma média total de 1/(1 −k) ocorrem fissões. Os reatores subcríticos propostos utilizam o fato de que uma reação nuclear sustentada por uma fonte de neutrões externa pode ser "desviada" quando a fonte de neutrões é removida. Isso proporciona um certo grau de segurança inerente.
k = 1 (criticalidade): Cada fissão causa uma média de mais uma fissão, levando a um nível de fissão (e poder) que é constante. Usinas nucleares operam com k = 1 a menos que o nível de potência esteja sendo aumentado ou diminuído.
k > 1 (supercrítica): Para cada fissão no material, é provável que haja "k"fissões depois do próximo tempo de geração média (A). O resultado é que o número de reações de fissão aumenta exponencialmente, de acordo com a equação $e^{(k-1)t/Lambda }$ , onde t é o tempo decorrido. As armas nucleares são projetadas para operar sob este estado. Existem duas subdivisões de supercrítica: pronta e atrasada.

Na descrição da cinética e dinâmica de reatores nucleares, e também na prática de operação do reator, é utilizado o conceito de reatividade, que caracteriza o desvio do reator do estado crítico: ρ = (k − 1)/k. InHour (de inverso de uma hora, às vezes abreviado ih ou inhr) é uma unidade de reatividade de um reator nuclear.

Em um reator nuclear, k oscilará de um pouco menos de 1 para um pouco mais de 1, devido principalmente a efeitos térmicos (à medida que mais energia é produzida, as varetas de combustível se aquecem e, portanto, se expandem, diminuindo sua taxa de captura e, assim, reduzindo k). Isso deixa o valor médio de k exatamente em 1. Os nêutrons atrasados desempenham um papel importante no tempo dessas oscilações.

A fórmula de seis fatores

O fator eficaz de multiplicação de neutrões $k$ pode ser descrito usando o produto de seis fatores de probabilidade que descrevem um sistema nuclear. Estes fatores, tradicionalmente organizados cronologicamente com relação à vida de um neutrônio em um reator térmico, incluem a probabilidade de rápida não fuga ${displaystyle P_{mathrm {FNL} }}$ , o fator de fissão rápida $varepsilon$ , a probabilidade de fuga de ressonância $p$ , a probabilidade de não fuga térmica ${displaystyle P_{mathrm {TNL} }}$ , o fator de utilização térmica $f$ , e o fator de reprodução de neutrões $eta$ (também chamado de fator de eficiência de nêutrons). A fórmula de seis fatores é tradicionalmente escrita da seguinte forma:

${displaystyle k=P_{mathrm {FNL} }varepsilon pP_{mathrm {TNL} }feta }$

Os fatores são descritos a seguir

PFNL{displaystyle P_{mathrm {FNL} }} ${displaystyle P_{mathrm {FNL} }}$ descreve a probabilidade de um nêutron rápido não escapar do sistema sem interagir.
- Os limites deste fator são 0 e 1, com um valor de 1 descrevendo um sistema para o qual os neutrões rápidos nunca escaparão sem interagir, ou seja, um sistema infinito.
- Também escrito como ${displaystyle L_{f}}$
ε ε - Sim. $varepsilon$ é a proporção de fissões totais a fissões causadas apenas por neutrões térmicos
- Os neutrões rápidos têm uma pequena probabilidade de causar fissões em urânio, especificamente Urânio-238.
- O fator de fissão rápida descreve a contribuição de fissões rápidas para o fator de multiplicação de neutrões eficaz
- Os limites deste fator são 1 e infinito, com um valor de 1 descrevendo um sistema para o qual apenas os neutrões térmicos estão causando fissões. Um valor de 2 denota um sistema em que os neutrões térmicos e rápidos estão causando quantidades iguais de fissões.
pNão. $p$ é a razão do número de neutrões que começam a termalização ao número de neutrões que atingem as energias térmicas.
- Muitos isótopos têm "ressonâncias" em suas curvas de seção transversal de captura que ocorrem em energias entre rápido e térmico.
- Se um nêutron começar a termalização (ou seja, começa a abrandar), há uma possibilidade que será absorvido por um material não multiplicador antes de atingir a energia térmica.
- Os limites deste fator são 0 e 1, com um valor de 1 descrevendo um sistema para o qual todos os neutrões rápidos que não vazam e não causam fissões rápidas eventualmente atingem energias térmicas.
PTNL{displaystyle P_{mathrm {TNL} }} ${displaystyle P_{mathrm {TNL} }}$ descreve a probabilidade de um nêutron térmico não escapar do sistema sem interagir.
- Os limites deste fator são 0 e 1, com um valor de 1 descrevendo um sistema para o qual os neutrões térmicos nunca escaparão sem interagir, ou seja, um sistema infinito.
- Também escrito como ${displaystyle L_{th}}$
fNão. $f$ é a proporção de número de neutrões térmicos absorvidos por núcleos físseis versus o número de neutrões absorvidos em todos os materiais do sistema.
- Este fator descreve a eficiência da utilização de nêutrons térmicos no sistema, daí o fator de utilização térmica do nome.
- Os limites deste fator são 0 e 1, com um valor de 1 descrevendo um sistema para o qual todo o sistema é feito de núcleos físseis (isto é, neutrões térmicos só podem reagir com materiais físseis). Da mesma forma, um valor de 0,5 descreve um sistema para o qual as reações com núcleos físseis e não físseis são iguais.
- Para um reator de energia nuclear convencional, este fator é o único que pode ser controlado diretamente pelo operador. Com manipulações para as hastes de controle, você pode aumentar a quantidade de neutrões sendo absorvidos em núcleos não-fisseis, enquanto diminui simultaneamente a quantidade de neutrões absorvidos em núcleos físseis.
? ? - Sim. $eta$ descreve a probabilidade de um nêutron absorvido causar uma fissão.
- Este fator descreve o comportamento do material físsil, especificamente se um nêutron é absorvido, o quão provável é causar uma fissão, e quantos nêutrons produz a fissão.

Em um meio infinito, o fator de multiplicação pode ser descrito pela fórmula de quatro fatores, que é o mesmo que descrito acima com ${displaystyle P_{mathrm {FNL} }}$ e ${displaystyle P_{mathrm {TNL} }}$ ambos iguais a 1.

Supercriticalidade imediata e atrasada

Nem todos os nêutrons são emitidos como produto direto da fissão; alguns são devidos ao decaimento radioativo de alguns dos fragmentos de fissão. Os nêutrons que ocorrem diretamente da fissão são chamados de "nêutrons imediatos", e os que são resultado do decaimento radioativo de fragmentos de fissão são chamados de "nêutrons retardados". A fração de nêutrons que estão atrasados é chamada de β, e essa fração é tipicamente inferior a 1% de todos os nêutrons na reação em cadeia.

Os nêutrons retardados permitem que um reator nuclear responda várias ordens de magnitude mais lentamente do que apenas os nêutrons imediatos fariam sozinhos. Sem nêutrons retardados, as mudanças nas taxas de reação em reatores nucleares ocorreriam em velocidades muito rápidas para o controle humano.

A região de supercriticalidade entre k = 1 e k = 1/(1−β) é conhecida como supercriticalidade atrasada (ou criticamente). É nessa região que operam todos os reatores nucleares. A região de supercriticalidade para k > 1/(1−β) é conhecido como prompt supercriticality (ou prompt criticality), que é a região na qual as armas nucleares operam.

A mudança em k necessária para ir de crítico para imediato crítico é definida como um dólar.

Aplicação de armas nucleares de multiplicação de nêutrons

Armas de fissão nuclear requerem uma massa de combustível físsil que é supercrítica.

Para uma dada massa de material físsil, o valor de k pode ser aumentado aumentando a densidade. Como a probabilidade por distância percorrida de um nêutron colidir com um núcleo é proporcional à densidade do material, aumentar a densidade de um material físsil pode aumentar k. Este conceito é utilizado no método de implosão para armas nucleares. Nesses dispositivos, a reação nuclear em cadeia começa após o aumento da densidade do material físsil com um explosivo convencional.

Na arma de fissão do tipo canhão, dois pedaços subcríticos de combustível são rapidamente reunidos. O valor de k para uma combinação de duas massas é sempre maior que o de seus componentes. A magnitude da diferença depende da distância, bem como da orientação física.

O valor de k também pode ser aumentado usando um refletor de nêutrons ao redor do material físsil

Uma vez que a massa de combustível é supercrítica, a potência aumenta exponencialmente. No entanto, o aumento de potência exponencial não pode continuar por muito tempo, pois k diminui quando a quantidade de material de fissão que resta diminui (ou seja, é consumido por fissões). Além disso, espera-se que a geometria e a densidade mudem durante a detonação, uma vez que o material de fissão restante é separado da explosão.

Predetonação

Se duas peças de material subcrítico não forem reunidas rapidamente o suficiente, a predetonação nuclear pode ocorrer, pelo qual uma explosão menor do que o esperado vai explodir a maior parte do material. Ver Fizzle (teste nuclear)

A detonação de uma arma nuclear envolve levar o material físsil ao seu estado supercrítico ideal muito rapidamente. Durante parte desse processo, a montagem é supercrítica, mas ainda não está em um estado ideal para uma reação em cadeia. Nêutrons livres, em particular de fissões espontâneas, podem fazer com que o dispositivo sofra uma reação em cadeia preliminar que destrói o material físsil antes que ele esteja pronto para produzir uma grande explosão, conhecida como pré-detonação.

Para manter a probabilidade de predetonação baixa, a duração do período de montagem não ideal é minimizada e materiais físseis e outros são usados com baixas taxas de fissão espontânea. De fato, a combinação de materiais deve ser tal que seja improvável que haja uma única fissão espontânea durante o período de montagem supercrítica. Em particular, o método da arma não pode ser usado com plutônio (ver projeto de armas nucleares).

Usinas nucleares e controle de reações em cadeia

As reações em cadeia naturalmente dão origem a taxas de reação que crescem (ou diminuem) exponencialmente, enquanto um reator de energia nuclear precisa ser capaz de manter a taxa de reação razoavelmente constante. Para manter esse controle, a criticidade da reação em cadeia deve ter uma escala de tempo lenta o suficiente para permitir a intervenção por efeitos adicionais (por exemplo, hastes de controle mecânico ou expansão térmica). Consequentemente, todos os reatores de energia nuclear (mesmo os reatores de nêutrons rápidos) dependem de nêutrons retardados para sua criticidade. Um reator de energia nuclear em operação flutua entre ser ligeiramente subcrítico e ligeiramente supercrítico retardado, mas deve sempre permanecer abaixo do imediato crítico.

É impossível para uma usina nuclear sofrer uma reação nuclear em cadeia que resulte em uma explosão de poder comparável a uma arma nuclear, mas mesmo explosões de baixa potência devido a reações em cadeia descontroladas (isso seria considerado " falhas em uma bomba) ainda podem causar danos consideráveis e derretimento em um reator. Por exemplo, o desastre de Chernobyl envolveu uma reação em cadeia descontrolada, mas o resultado foi uma explosão de vapor de baixa potência devido à liberação relativamente pequena de calor, em comparação com uma bomba. No entanto, o complexo do reator foi destruído pelo calor, bem como pela queima ordinária do grafite exposto ao ar. Tais explosões de vapor seriam típicas da montagem muito difusa de materiais em um reator nuclear, mesmo sob as piores condições.

Além disso, outras medidas podem ser tomadas para segurança. Por exemplo, as usinas de energia licenciadas nos Estados Unidos exigem um coeficiente de reatividade negativo (isso significa que, se o refrigerante for removido do núcleo do reator, a reação nuclear tenderá a parar, não aumentar). Isso elimina a possibilidade do tipo de acidente ocorrido em Chernobyl (devido a um coeficiente de vazio positivo). No entanto, os reatores nucleares ainda são capazes de causar explosões menores mesmo após o desligamento completo, como foi o caso do desastre nuclear de Fukushima Daiichi. Nesses casos, o calor de decaimento residual do núcleo pode causar altas temperaturas se houver perda de fluxo de refrigerante, mesmo um dia após o desligamento da reação em cadeia (consulte SCRAM). Isso pode causar uma reação química entre a água e o combustível que produz gás hidrogênio, que pode explodir após a mistura com o ar, com graves consequências de contaminação, pois o material da vareta combustível ainda pode ficar exposto à atmosfera a partir desse processo. No entanto, tais explosões não acontecem durante uma reação em cadeia, mas sim como resultado da energia do decaimento beta radioativo, depois que a reação em cadeia da fissão foi interrompida.

Más resultados...