Processo adiabático

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Processo termodinâmico em que nenhuma massa ou calor é trocada com ambientes

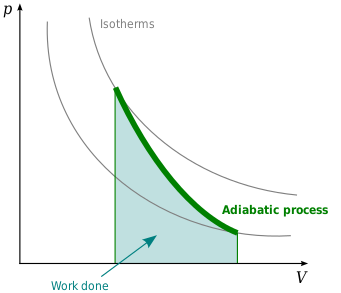
Em termodinâmica, um processo adiabático (em grego: adiábatos, "intransponível") é um tipo de processo termodinâmico que ocorre sem transferência de calor ou massa entre o sistema termodinâmico e seu ambiente. Ao contrário de um processo isotérmico, um processo adiabático transfere energia para o ambiente apenas como trabalho. Como um conceito-chave na termodinâmica, o processo adiabático suporta a teoria que explica a primeira lei da termodinâmica.

Alguns processos químicos e físicos ocorrem muito rapidamente para que a energia entre ou saia do sistema como calor, permitindo uma "aproximação adiabática" conveniente. Por exemplo, a temperatura adiabática da chama usa essa aproximação para calcular o limite superior da temperatura da chama assumindo que a combustão não perde calor para o ambiente.

Em meteorologia e oceanografia, o resfriamento adiabático produz condensação de umidade ou salinidade, supersaturando a parcela. Portanto, o excesso deve ser removido. Lá, o processo se torna um processo pseudo-adiabático pelo qual a água líquida ou o sal que condensa é considerado removido após a formação por precipitação instantânea idealizada. O processo pseudoadiabático é definido apenas para expansão porque uma parcela comprimida se torna mais quente e permanece subsaturada.

Descrição

Um processo sem transferência de calor para ou de um sistema, de modo que $Q = 0$ , é chamado de adiabático, e tal sistema é dito ser isolado adiabaticamente. A suposição simplificadora freqüentemente feita é que um processo é adiabático. Por exemplo, supõe-se que a compressão de um gás dentro de um cilindro de um motor ocorra tão rapidamente que, na escala de tempo do processo de compressão, pouca energia do sistema pode ser transferida como calor para o ambiente. Mesmo que os cilindros não sejam isolados e sejam bastante condutores, esse processo é idealizado para ser adiabático. O mesmo pode ser dito para o processo de expansão de tal sistema.

A suposição de isolamento adiabático é útil e frequentemente combinada com outras idealizações para calcular uma boa primeira aproximação do comportamento de um sistema. Por exemplo, de acordo com Laplace, quando o som viaja em um gás, não há tempo para condução de calor no meio e, portanto, a propagação do som é adiabática. Para tal processo adiabático, o módulo de elasticidade (módulo de Young) pode ser expresso como $E = γP$ , onde $γ$ é a razão de calores específicos a pressão constante e a volume constante ( $γ = C p / C v$ ) e $P$ é a pressão do gás.

Várias aplicações da hipótese adiabática

Para um sistema fechado, pode-se escrever a primeira lei da termodinâmica como: $Δ U = Q - W$ , onde $Δ U$ denota a variação da energia interna do sistema, $Q$ a quantidade de energia adicionada a ele como calor e $W$ o trabalho realizado pelo sistema em seu entorno.

Se o sistema tem tais paredes rígidas que o trabalho não pode ser transferido dentro ou fora ( $W = 0$ ), e as paredes não são adiabáticas e a energia é adicionada na forma de calor ( $Q > 0$ ), e não há mudança de fase, então a temperatura do sistema aumentará.
Se o sistema tem tais paredes rígidas que o trabalho de pressão-volume não pode ser feito, mas as paredes são adiabáticas ( $Q = 0$ ), e a energia é adicionada como o trabalho isocórico (volume constante) na forma de atrito ou a agitação de um fluido viscoso dentro do sistema ( $W < 0$ ), e não há mudança de fase, então a temperatura do sistema aumentará.
Se as paredes do sistema são adiabáticas ( $Q = 0$ ) mas não rígido ( $W \neq 0$ ), e, em um processo idealizado fictício, a energia é adicionada ao sistema na forma de trabalho sem atrito, pressão não viscosa ( $W < 0$ ), e não há mudança de fase, então a temperatura do sistema aumentará. Tal processo é chamado de processo isentropic e é dito ser "reversível". Idealmente, se o processo fosse invertido a energia poderia ser recuperada inteiramente como trabalho feito pelo sistema. Se o sistema contém um gás compressível e é reduzido em volume, a incerteza da posição do gás é reduzida, e aparentemente reduziria a entropia do sistema, mas a temperatura do sistema aumentará à medida que o processo é isentropic ( $? S = 0$ ). Se o trabalho for adicionado de tal forma que as forças de atrito ou viscosas estão operando dentro do sistema, então o processo não é isentropic, e se não houver mudança de fase, então a temperatura do sistema aumentará, o processo é dito ser "irrversível", e o trabalho adicionado ao sistema não é inteiramente recuperável na forma de trabalho.
Se as paredes de um sistema não são adiabáticas, e a energia é transferida como calor, a entropia é transferida para o sistema com o calor. Tal processo não é nem adiabático nem isentrópico, tendo $Q > 0$ e $? S > 0$ segundo a segunda lei da termodinâmica.

Os processos adiabáticos que ocorrem naturalmente são irreversíveis (é produzida entropia).

A transferência de energia como trabalho em um sistema adiabaticamente isolado pode ser imaginada como sendo de dois tipos extremos idealizados. Em um desses tipos, nenhuma entropia é produzida dentro do sistema (sem atrito, dissipação viscosa, etc.), e o trabalho é apenas pressão-volume (denotado por $P d V$ ). Na natureza, esse tipo ideal ocorre apenas aproximadamente porque exige um processo infinitamente lento e nenhuma fonte de dissipação.

O outro tipo de trabalho extremo é o trabalho isocórico ( $d V = 0$ ), para o qual a energia é adicionada como trabalho apenas por atrito ou viscosidade dissipação dentro do sistema. Um agitador que transfere energia para um fluido viscoso de um sistema isolado adiabaticamente com paredes rígidas, sem mudança de fase, causará um aumento na temperatura do fluido, mas esse trabalho não é recuperável. O trabalho isocórico é irreversível. A segunda lei da termodinâmica observa que um processo natural, de transferência de energia como trabalho, sempre consiste pelo menos em trabalho isocórico e frequentemente em ambos os tipos extremos de trabalho. Todo processo natural, adiabático ou não, é irreversível, com $Δ S > 0$ , pois o atrito ou a viscosidade estão sempre presentes em alguma extensão.

Aquecimento e resfriamento adiabático

A compressão adiabática de um gás causa um aumento na temperatura do gás. A expansão adiabática contra a pressão, ou uma mola, causa uma queda na temperatura. Em contraste, a expansão livre é um processo isotérmico para um gás ideal.

Aquecimento adiabático ocorre quando a pressão de um gás é aumentada pelo trabalho feito sobre ele por seus arredores, por exemplo, um pistão comprimindo um gás contido em um cilindro e elevando a temperatura em muitas situações práticas a condução de calor através das paredes pode ser lenta em comparação com o tempo de compressão. Isso encontra aplicação prática em motores a diesel que dependem da falta de dissipação de calor durante o curso de compressão para elevar a temperatura do vapor do combustível o suficiente para igní-lo.

O aquecimento adiabático ocorre na atmosfera da Terra quando uma massa de ar desce, por exemplo, em um vento catabático, vento Foehn ou vento Chinook fluindo para baixo sobre uma cordilheira. Quando uma parcela de ar desce, a pressão na parcela aumenta. Por causa desse aumento de pressão, o volume da parcela diminui e sua temperatura aumenta à medida que é realizado trabalho sobre a parcela de ar, aumentando assim sua energia interna, que se manifesta pelo aumento da temperatura dessa massa de ar. A parcela de ar só pode dissipar lentamente a energia por condução ou radiação (calor) e, em uma primeira aproximação, pode ser considerada isolada adiabaticamente e o processo um processo adiabático.

O resfriamento adiabático ocorre quando a pressão em um sistema isolado adiabaticamente é diminuída, permitindo que ele se expanda, fazendo com que ele realize trabalho em seus arredores. Quando a pressão aplicada a uma parcela de gás é reduzida, permite-se que o gás na parcela se expanda; à medida que o volume aumenta, a temperatura cai à medida que sua energia interna diminui. O resfriamento adiabático ocorre na atmosfera da Terra com elevação orográfica e ondas de sotavento, podendo formar pilei ou nuvens lenticulares.

Devido em parte ao resfriamento adiabático em áreas montanhosas, a queda de neve ocorre com pouca frequência em algumas partes do deserto do Saara.

O resfriamento adiabático não precisa envolver um fluido. Uma técnica usada para atingir temperaturas muito baixas (milésimos e até milionésimos de grau acima do zero absoluto) é via desmagnetização adiabática, onde a mudança no campo magnético em um material magnético é usada para fornecer resfriamento adiabático. Além disso, o conteúdo de um universo em expansão pode ser descrito (em primeira ordem) como um fluido de resfriamento adiabático. (Veja a morte térmica do universo.)

O magma ascendente também sofre resfriamento adiabático antes da erupção, particularmente significativo no caso de magmas que sobem rapidamente de grandes profundidades, como os kimberlitos.

No manto de convecção da Terra (a astenosfera) abaixo da litosfera, a temperatura do manto é aproximadamente um adiabat. A ligeira diminuição da temperatura com a profundidade rasa é devida à diminuição da pressão quanto mais raso o material estiver na Terra.

Essas mudanças de temperatura podem ser quantificadas usando a lei dos gases ideais ou a equação hidrostática para processos atmosféricos.

Na prática, nenhum processo é verdadeiramente adiabático. Muitos processos dependem de uma grande diferença nas escalas de tempo do processo de interesse e na taxa de dissipação de calor através de um limite do sistema e, portanto, são aproximados usando uma suposição adiabática. Sempre há alguma perda de calor, pois não existem isoladores perfeitos.

Gás ideal (processo reversível)

Para uma substância simples, durante um processo adiabático em que o volume aumenta, a energia interna da substância de trabalho deve diminuir

A equação matemática para um gás ideal passando por um processo adiabático reversível (isto é, sem geração de entropia) pode ser representada pela equação do processo politrópico

{displaystyle PV^{gamma }={text{constant}},}

onde $P$ é a pressão, $V$ é o volume, e $γ$ é o índice adiabático ou taxa de capacidade térmica definida como

{displaystyle gamma ={frac {C_{P}}{C_{V}}}={frac {f+2}{f}}.}

Aqui $C P$ é o calor específico para pressão constante, $C V$ é o calor específico para volume constante e $f$ é o número de graus de liberdade (3 para um gás monoatômico, 5 para um gás diatômico ou um gás de moléculas lineares como o dióxido de carbono).

Para um gás ideal monoatômico, $γ = 5 / 3$ , e para um gás diatômico (como nitrogênio e oxigênio, os principais componentes do ar), $γ = 7 / 5$ . Observe que a fórmula acima é aplicável apenas a gases ideais clássicos (isto é, gases muito acima da temperatura do zero absoluto) e não a gases Bose-Einstein ou Fermi.

Pode-se também usar a lei dos gases ideais para reescrever a relação acima entre $P$ e $V$ como

{displaystyle P^{1-gamma }T^{gamma }={text{constant}},}

{displaystyle TV^{gamma -1}={text{constant}}.}

onde T é a temperatura absoluta ou termodinâmica.

Exemplo de compressão adiabática

O curso de compressão em um motor a gasolina pode ser usado como exemplo de compressão adiabática. As suposições do modelo são: o volume não comprimido do cilindro é um litro (1 L = 1000 cm³ = 0,001 m³); o gás dentro é o ar que consiste apenas em nitrogênio molecular e oxigênio (portanto, um gás diatômico com 5 graus de liberdade e, portanto, $γ = 7 / 5$ ); a taxa de compressão do motor é 10:1 (ou seja, o volume de 1 L de gás não comprimido é reduzido para 0,1 L pelo pistão); e o gás não comprimido está aproximadamente à temperatura e pressão ambiente (uma temperatura ambiente quente de ~27 °C ou 300 K e uma pressão de 1 bar = 100 kPa, ou seja, pressão atmosférica típica ao nível do mar).

{displaystyle {begin{aligned}&P_{1}V_{1}^{gamma }=mathrm {constant} _{1}=100,000~{text{Pa}}times (0.001~{text{m}}^{3})^{frac {7}{5}}\&=10^{5}times 6.31times 10^{-5}~{text{Pa}},{text{m}}^{21/5}=6.31~{text{Pa}},{text{m}}^{21/5},end{aligned}}}

portanto, a constante adiabática para este exemplo é de cerca de 6,31 Pa m^4,2.

O gás agora está comprimido em um volume de 0,1 L (0,0001 m³), que supomos que aconteça rápido o suficiente para que nenhum calor entre ou saia do gás pelas paredes. A constante adiabática permanece a mesma, mas com a pressão resultante desconhecida

{displaystyle P_{2}V_{2}^{gamma }=mathrm {constant} _{1}=6.31~{text{Pa}},{text{m}}^{21/5}=Ptimes (0.0001~{text{m}}^{3})^{frac {7}{5}},}

Agora podemos calcular a pressão final

{displaystyle P_{2}=P_{1}left({frac {V_{1}}{V_{2}}}right)^{gamma }=100,000~{text{Pa}}times {text{10}}^{7/5}=2.51times 10^{6}~{text{Pa}}}

ou 25,1 bar. Esse aumento de pressão é mais do que uma simples taxa de compressão de 10:1 indicaria; isso ocorre porque o gás não é apenas comprimido, mas o trabalho realizado para comprimi-lo também aumenta sua energia interna, que se manifesta por um aumento na temperatura do gás e um aumento adicional na pressão acima do que resultaria de um cálculo simplista de 10 vezes a pressão original.

Também podemos calcular a temperatura do gás comprimido no cilindro do motor usando a lei dos gases ideais, PV = nRT (n é a quantidade de gás em moles e R a constante do gás para esse gás). Sendo nossas condições iniciais 100 kPa de pressão, 1 L de volume e 300 K de temperatura, nossa constante experimental (nR) é:

{displaystyle {frac {PV}{T}}=mathrm {constant} _{2}={frac {10^{5}~{text{Pa}}times 10^{-3}~{text{m}}^{3}}{300~{text{K}}}}=0.333~{text{Pa}},{text{m}}^{3}{text{K}}^{-1}.}

Sabemos que o gás comprimido tem $V$ = 0,1 L e $P$ = 2,51×10⁶ Pa, então podemos calcular a temperatura:

{displaystyle T={frac {PV}{mathrm {constant} _{2}}}={frac {2.51times 10^{6}~{text{Pa}}times 10^{-4}~{text{m}}^{3}}{0.333~{text{Pa}},{text{m}}^{3}{text{K}}^{-1}}}=753~{text{K}}.}

Essa é uma temperatura final de 753 K, ou 479 °C, ou 896 °F, bem acima do ponto de ignição de muitos combustíveis. É por isso que um motor de alta compressão requer combustíveis especialmente formulados para não se auto-inflamar (o que causaria detonação do motor quando operado nessas condições de temperatura e pressão), ou que um superalimentador com intercooler para fornecer um aumento de pressão, mas com menor aumento de temperatura seria vantajoso. Um motor a diesel opera em condições ainda mais extremas, sendo típicas taxas de compressão de 16:1 ou mais, para fornecer uma temperatura de gás muito alta, o que garante a ignição imediata do combustível injetado.

Expansão livre adiabática de um gás

Para uma expansão livre adiabática de um gás ideal, o gás é contido em um recipiente isolado e então expandido no vácuo. Como não há pressão externa contra a qual o gás se expanda, o trabalho realizado pelo ou sobre o sistema é zero. Como esse processo não envolve nenhuma transferência de calor ou trabalho, a primeira lei da termodinâmica implica que a variação líquida da energia interna do sistema é zero. Para um gás ideal, a temperatura permanece constante porque a energia interna depende apenas da temperatura nesse caso. Como a temperatura constante a entropia é proporcional ao volume, a entropia aumenta neste caso, portanto este processo é irreversível.

Derivação da relação P–V para aquecimento e resfriamento adiabático

A definição de um processo adiabático é que a transferência de calor para o sistema é zero, $δQ = 0$ . Então, de acordo com a primeira lei da termodinâmica,

{displaystyle dU+delta W=delta Q=0,}

(A1)

onde $dU$ é a variação da energia interna do sistema e $δW$ é o trabalho feito pelo sistema. Qualquer trabalho ( $δW$ ) feito deve ser feito à custa de energia interna $U$ , já que nenhum calor $δQ$ está sendo fornecido do ambiente. O trabalho pressão-volume $δW$ realizado pelo sistema é definido como

{displaystyle delta W=P,dV.}

(a2)

No entanto, $P$ não permanece constante durante um processo adiabático, mas muda junto com $V$ .

Deseja-se saber como os valores de $dP$ e $dV$ relacionam-se entre si à medida que o processo adiabático prossegue. Para um gás ideal (lembre-se da lei do gás ideal $PV = nRT$ ) a energia interna é dada por

{displaystyle U=alpha nRT=alpha PV,}

(A3)

onde $α$ é o número de graus de liberdade dividido por 2, $R$ é a constante universal dos gases e $n$ é o número de moles no sistema (uma constante).

A equação de diferenciação (a3) produz

{displaystyle dU=alpha nR,dT=alpha ,d(PV)=alpha (P,dV+V,dP).}

(A4)

A equação (a4) é frequentemente expressa como $dU = nC V dT$ porque $C V = αR$ .

Agora substitua as equações (a2) e (a4) na equação (a1) para obter

-P , dV = alpha P , dV + alpha V , dP,

fatorize $- P dV$ :

{displaystyle -(alpha +1)P,dV=alpha V,dP,}

e divida ambos os lados por $PV$ :

{displaystyle -(alpha +1){frac {dV}{V}}=alpha {frac {dP}{P}}.}

Depois de integrar os lados esquerdo e direito de $V 0$ a $V$ e de $P 0$ a $P$ e mudando os lados respectivamente,

{displaystyle ln left({frac {P}{P_{0}}}right)=-{frac {alpha +1}{alpha }}ln left({frac {V}{V_{0}}}right).}

Exponencialize ambos os lados, substitua $α + 1 / α$ com $γ$ , a taxa de capacidade de calor

{displaystyle left({frac {P}{P_{0}}}right)=left({frac {V}{V_{0}}}right)^{-gamma },}

e elimine o sinal negativo para obter

{displaystyle left({frac {P}{P_{0}}}right)=left({frac {V_{0}}{V}}right)^{gamma }.}

Portanto,

{displaystyle left({frac {P}{P_{0}}}right)left({frac {V}{V_{0}}}right)^{gamma }=1,}

{displaystyle P_{0}V_{0}^{gamma }=PV^{gamma }=mathrm {constant}.}

{displaystyle Delta U=alpha RnT_{2}-alpha RnT_{1}=alpha RnDelta T.}

(B1)

Ao mesmo tempo, o trabalho realizado pelas mudanças de pressão-volume como resultado desse processo é igual a

{displaystyle W=int _{V_{1}}^{V_{2}}P,dV.}

(b2)

Como exigimos que o processo seja adiabático, a seguinte equação precisa ser verdadeira

{displaystyle Delta U+W=0.}

(b))

Pela derivação anterior,

{displaystyle PV^{gamma }={text{constant}}=P_{1}V_{1}^{gamma }.}

(b))

Reorganizando (b4) dá

{displaystyle P=P_{1}left({frac {V_{1}}{V}}right)^{gamma }.}

Substituir isso em (b2) dá

{displaystyle W=int _{V_{1}}^{V_{2}}P_{1}left({frac {V_{1}}{V}}right)^{gamma },dV.}

Integrando obtemos a expressão para trabalho,

{displaystyle W=P_{1}V_{1}^{gamma }{frac {V_{2}^{1-gamma }-V_{1}^{1-gamma }}{1-gamma }}={frac {P_{2}V_{2}-P_{1}V_{1}}{1-gamma }}.}

Substituindo $γ = α + 1 / α$ no segundo mandato,

{displaystyle W=-alpha P_{1}V_{1}^{gamma }left(V_{2}^{1-gamma }-V_{1}^{1-gamma }right).}

Reorganizando,

{displaystyle W=-alpha P_{1}V_{1}left(left({frac {V_{2}}{V_{1}}}right)^{1-gamma }-1right).}

Usando a lei dos gases ideais e assumindo uma quantidade molar constante (como costuma acontecer em casos práticos),

{displaystyle W=-alpha nRT_{1}left(left({frac {V_{2}}{V_{1}}}right)^{1-gamma }-1right).}

Pela fórmula contínua,

{displaystyle {frac {P_{2}}{P_{1}}}=left({frac {V_{2}}{V_{1}}}right)^{-gamma },}

{displaystyle left({frac {P_{2}}{P_{1}}}right)^{-{frac {1}{gamma }}}={frac {V_{2}}{V_{1}}}.}

Substituindo na expressão anterior por $W$ ,

{displaystyle W=-alpha nRT_{1}left(left({frac {P_{2}}{P_{1}}}right)^{frac {gamma -1}{gamma }}-1right).}

Substituir esta expressão e (b1) em (b3) dá

{displaystyle alpha nR(T_{2}-T_{1})=alpha nRT_{1}left(left({frac {P_{2}}{P_{1}}}right)^{frac {gamma -1}{gamma }}-1right).}

Simplificando,

{displaystyle T_{2}-T_{1}=T_{1}left(left({frac {P_{2}}{P_{1}}}right)^{frac {gamma -1}{gamma }}-1right),}

{displaystyle {frac {T_{2}}{T_{1}}}-1=left({frac {P_{2}}{P_{1}}}right)^{frac {gamma -1}{gamma }}-1,}

{displaystyle T_{2}=T_{1}left({frac {P_{2}}{P_{1}}}right)^{frac {gamma -1}{gamma }}.}

Derivação de fórmula discreta e expressão de trabalho

A mudança na energia interna de um sistema, medida do estado 1 ao estado 2, é igual a

Ao mesmo tempo, o trabalho realizado pelas mudanças de pressão-volume como resultado desse processo é igual a

{displaystyle W=int _{V_{1}}^{V_{2}}P,dV.}

(c2)

Como exigimos que o processo seja adiabático, a seguinte equação precisa ser verdadeira

{displaystyle Delta U+W=0.}

(c3)

Pela derivação anterior,

{displaystyle PV^{gamma }={text{constant}}=P_{1}V_{1}^{gamma }.}

(C4)

Reorganizando (c4) dá

{displaystyle P=P_{1}left({frac {V_{1}}{V}}right)^{gamma }.}

Substituir isso em (c2) dá

{displaystyle W=int _{V_{1}}^{V_{2}}P_{1}left({frac {V_{1}}{V}}right)^{gamma },dV.}

Integrando obtemos a expressão para trabalho,

{displaystyle W=P_{1}V_{1}^{gamma }{frac {V_{2}^{1-gamma }-V_{1}^{1-gamma }}{1-gamma }}={frac {P_{2}V_{2}-P_{1}V_{1}}{1-gamma }}.}

Substituindo $γ = α + 1 / α$ no segundo mandato,

{displaystyle W=-alpha P_{1}V_{1}^{gamma }left(V_{2}^{1-gamma }-V_{1}^{1-gamma }right).}

Reorganizando,

{displaystyle W=-alpha P_{1}V_{1}left(left({frac {V_{2}}{V_{1}}}right)^{1-gamma }-1right).}

Usando a lei dos gases ideais e assumindo uma quantidade molar constante (como costuma acontecer em casos práticos),

{displaystyle W=-alpha nRT_{1}left(left({frac {V_{2}}{V_{1}}}right)^{1-gamma }-1right).}

Pela fórmula contínua,

{displaystyle {frac {P_{2}}{P_{1}}}=left({frac {V_{2}}{V_{1}}}right)^{-gamma },}

{displaystyle left({frac {P_{2}}{P_{1}}}right)^{-{frac {1}{gamma }}}={frac {V_{2}}{V_{1}}}.}

Substituindo na expressão anterior por $W$ ,

{displaystyle W=-alpha nRT_{1}left(left({frac {P_{2}}{P_{1}}}right)^{frac {gamma -1}{gamma }}-1right).}

Substituir esta expressão e (c1) em (c3) dá

{displaystyle alpha nR(T_{2}-T_{1})=alpha nRT_{1}left(left({frac {P_{2}}{P_{1}}}right)^{frac {gamma -1}{gamma }}-1right).}

Simplificando,

{displaystyle T_{2}-T_{1}=T_{1}left(left({frac {P_{2}}{P_{1}}}right)^{frac {gamma -1}{gamma }}-1right),}

{displaystyle {frac {T_{2}}{T_{1}}}-1=left({frac {P_{2}}{P_{1}}}right)^{frac {gamma -1}{gamma }}-1,}

{displaystyle T_{2}=T_{1}left({frac {P_{2}}{P_{1}}}right)^{frac {gamma -1}{gamma }}.}

Gráficos de adiabás

Um adiabat é uma curva de entropia constante em um diagrama. Algumas propriedades de adiabats em um diagrama P–V são indicadas. Estas propriedades podem ser lidas a partir do comportamento clássico dos gases ideais, exceto na região onde PV se torna pequeno (baixa temperatura), onde os efeitos quânticos se tornam importantes.

Cada adiabate assintoticamente se aproxima tanto do V eixo e o P eixo (como isotérmicas).
Cada adiabat interseta cada isotérmica exatamente uma vez.
Um adiabat parece semelhante a um isotérmico, exceto que durante uma expansão, um adiabat perde mais pressão do que um isotérmico, por isso tem uma inclinação mais íngreme (mais vertical).
Se os isotérmicos são côncavos para a direção nordeste (45°), então os adiabates são côncavos para o nordeste oriental (31°).
Se os adiabates e isotérmicos são grafos em intervalos regulares de entropia e temperatura, respectivamente (como altitude em um mapa de contorno), então como o olho se move para os eixos (para o sudoeste), vê a densidade de isotérmicas permanecer constante, mas vê a densidade de adiabates crescer. A exceção é muito perto de zero absoluto, onde a densidade de adiabates cai acentuadamente e eles se tornam raros (veja o teorema de Nernst).

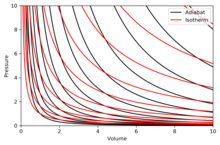
O diagrama da direita é um diagrama P–V com uma superposição de adiabatas e isotermas:

As isotermas são as curvas vermelhas e as adiabatas são as curvas pretas.

Os adiabats são isentrópicos.

O volume é o eixo horizontal e a pressão é o eixo vertical.

Etimologia

O termo adiabático () é uma anglicização do termo grego ἀδιάβατος "intransponível" (usado por Xenofonte dos rios). É usado no sentido termodinâmico por Rankine (1866) e adotado por Maxwell em 1871 (atribuindo explicitamente o termo a Rankine). A origem etimológica corresponde aqui a uma impossibilidade de transferência de energia sob a forma de calor e de transferência de matéria através da parede.

A palavra grega ἀδιάβατος é formada a partir do privativo ἀ- ("não") e διαβατός, "passável", por sua vez derivado de διά ("através"), e βαῖνειν ("andar, ir, vir").

Significado conceitual na teoria termodinâmica

O processo adiabático tem sido importante para a termodinâmica desde seus primórdios. Foi importante no trabalho de Joule porque forneceu uma maneira quase direta de relacionar quantidades de calor e trabalho.

A energia pode entrar ou sair de um sistema termodinâmico fechado por paredes que impedem a transferência de massa apenas como calor ou trabalho. Portanto, uma quantidade de trabalho em tal sistema pode ser relacionada quase diretamente a uma quantidade equivalente de calor em um ciclo de dois membros. O primeiro membro é um processo de trabalho adiabático isocórico aumentando a energia interna do sistema; a segunda, uma transferência de calor isocórica e sem trabalho, retornando o sistema ao seu estado original. Conseqüentemente, Rankine media a quantidade de calor em unidades de trabalho, e não como uma quantidade calorimétrica. Em 1854, Rankine usou uma quantidade que chamou de "a função termodinâmica" isso mais tarde foi chamado de entropia e, naquela época, ele também escreveu sobre a "curva sem transmissão de calor", que mais tarde chamou de curva adiabática. Além de seus dois membros isotérmicos, o ciclo de Carnot possui dois membros adiabáticos.

Para os fundamentos da termodinâmica, a importância conceitual desta foi enfatizada por Bryan, por Carathéodory e por Born. A razão é que a calorimetria pressupõe um tipo de temperatura já definida antes da declaração da primeira lei da termodinâmica, como aquela baseada em escalas empíricas. Tal pressuposição envolve fazer a distinção entre temperatura empírica e temperatura absoluta. Em vez disso, é melhor deixar a definição de temperatura termodinâmica absoluta até que a segunda lei esteja disponível como base conceitual.

No século XVIII, a lei da conservação da energia ainda não estava totalmente formulada ou estabelecida, e a natureza do calor era debatida. Uma abordagem para esses problemas era considerar o calor, medido por calorimetria, como uma substância primária que é conservada em quantidade. Em meados do século XIX, foi reconhecida como uma forma de energia, e a lei da conservação da energia também foi reconhecida. A visão que finalmente se estabeleceu, e atualmente é considerada correta, é que a lei da conservação da energia é um axioma primário e que o calor deve ser analisado como consequência. Nesta luz, o calor não pode ser um componente da energia total de um único corpo porque não é uma variável de estado, mas sim uma variável que descreve uma transferência entre dois corpos. O processo adiabático é importante porque é um ingrediente lógico dessa visão atual.

Usos divergentes da palavra adiabático

Este artigo é escrito do ponto de vista da termodinâmica macroscópica, e a palavra adiabático é usada neste artigo da maneira tradicional da termodinâmica, introduzida por Rankine. É apontado no presente artigo que, por exemplo, se a compressão de um gás é rápida, então há pouco tempo para ocorrer a transferência de calor, mesmo quando o gás não está isolado adiabaticamente por uma parede definida. Nesse sentido, uma compressão rápida de um gás é, às vezes, aproximadamente ou vagamente considerada adiabática, embora muitas vezes longe de ser isentrópica, mesmo quando o gás não está isolado adiabaticamente por uma parede definida.

A mecânica quântica e a mecânica estatística quântica, no entanto, usam a palavra adiabática em um sentido muito diferente, que às vezes pode parecer quase oposto ao sentido termodinâmico clássico. Na teoria quântica, a palavra adiabático pode significar algo talvez quase isentrópico, ou talvez quase estático, mas o uso da palavra é muito diferente entre as duas disciplinas.

Por um lado, na teoria quântica, se um elemento perturbativo de trabalho compressivo é feito quase infinitamente devagar (ou seja, quase estaticamente), diz-se que foi feito adiabaticamente. A ideia é que as formas das autofunções mudem lenta e continuamente, de modo que nenhum salto quântico seja acionado e a mudança seja virtualmente reversível. Embora os números de ocupação permaneçam inalterados, há uma mudança nos níveis de energia dos autoestados correspondentes um-para-um, pré e pós-compressão. Assim, um elemento perturbativo de trabalho foi feito sem transferência de calor e sem introdução de mudança aleatória dentro do sistema. Por exemplo, Max Born escreve "Na verdade, geralmente é o 'adiabático' caso com o qual temos que lidar: ou seja, o caso limite em que a força externa (ou a reação das partes do sistema entre si) age muito lentamente. Neste caso, com uma aproximação muito alta

c_1^2=1,,,c_2^2=0,,,c_3^2=0,,...,,

isto é, não há probabilidade de uma transição e o sistema está no estado inicial após o término da perturbação. Tal perturbação lenta é, portanto, reversível, como é classicamente."

Por outro lado, na teoria quântica, se um elemento perturbativo de trabalho compressivo é feito rapidamente, ele muda os números de ocupação e as energias dos autoestados em proporção à integral do momento de transição e de acordo com a teoria de perturbação dependente do tempo, assim como perturbar a forma funcional dos próprios autoestados. Nessa teoria, diz-se que uma mudança tão rápida não é adiabática, e a palavra contrária diabática é aplicada a ela.

Pesquisas recentes sugerem que a potência absorvida da perturbação corresponde à taxa dessas transições não adiabáticas. Isso corresponde ao processo clássico de transferência de energia na forma de calor, mas com as escalas de tempo relativas invertidas no caso quântico. Os processos adiabáticos quânticos ocorrem em escalas de tempo relativamente longas, enquanto os processos adiabáticos clássicos ocorrem em escalas de tempo relativamente curtas. Também deve ser notado que o conceito de 'calor' (em referência à quantidade de energia térmica transferida) se decompõe no nível quântico, e a forma específica de energia (normalmente eletromagnética) deve ser considerada. A absorção pequena ou insignificante de energia da perturbação em um processo adiabático quântico fornece uma boa justificativa para identificá-lo como o análogo quântico dos processos adiabáticos na termodinâmica clássica e para a reutilização do termo.

Além disso, em termodinâmica atmosférica, um processo diabático é aquele em que o calor é trocado.

Na termodinâmica clássica, uma mudança tão rápida ainda seria chamada de adiabática porque o sistema é adiabaticamente isolado e não há transferência de energia na forma de calor. A forte irreversibilidade da mudança, devido à viscosidade ou outra produção de entropia, não afeta esse uso clássico.

Assim, para uma massa de gás, na termodinâmica macroscópica, as palavras são usadas de tal forma que uma compressão às vezes é vagamente ou aproximadamente considerada adiabática se for rápida o suficiente para evitar a transferência de calor, mesmo que o sistema não esteja isolado adiabaticamente. Mas na teoria estatística quântica, uma compressão não é chamada de adiabática se for rápida, mesmo que o sistema seja adiabaticamente isolado no sentido termodinâmico clássico do termo. As palavras são usadas de forma diferente nas duas disciplinas, como afirmado logo acima.

Contenido relacionado

Más resultados...