Particionamento de espaço binário

Na ciência da computação, particionamento de espaço binário (BSP) é um método para particionamento de espaço que subdivide recursivamente um espaço euclidiano em dois conjuntos convexos usando hiperplanos como partições. Este processo de subdivisão dá origem a uma representação de objetos dentro do espaço na forma de uma estrutura de dados em árvore conhecida como árvore BSP.

O particionamento de espaço binário foi desenvolvido no contexto da computação gráfica 3D em 1969. A estrutura de uma árvore BSP é útil na renderização porque pode fornecer com eficiência informações espaciais sobre os objetos em uma cena, como objetos sendo ordenados de frente para frente. consecutivamente em relação a um espectador em um determinado local. Outras aplicações do BSP incluem: realização de operações geométricas com formas (geometria sólida construtiva) em CAD, detecção de colisões em robótica e videogames 3D, traçado de raios e outras aplicações que envolvem o manuseio de cenas espaciais complexas.

Histórico

• 1969 Schumacker et al. publicaram um relatório que descreveu como os planos cuidadosamente posicionados em um ambiente virtual poderiam ser usados para acelerar o ordenamento do polígono. A técnica feita uso de coerência de profundidade, que afirma que um polígono no lado distante do plano não pode, de qualquer forma, obstruir um polígono mais próximo. Isso foi usado em simuladores de voo feitos pela GE, bem como Evans e Sutherland. No entanto, a criação da organização de dados poligonais foi realizada manualmente pelo designer de cena.

• 1980 Fuchs et al. estendeu a ideia de Schumacker para a representação de objetos 3D em um ambiente virtual usando aviões que estão coincidentes com polígonos para particionar recursivamente o espaço 3D. Isso forneceu uma geração totalmente automatizada e algorítmica de uma estrutura de dados poligonais hierárquica conhecida como uma Árvore de Partição Espacial Binária (BSP Tree). O processo teve lugar como uma etapa de pré-processamento off-line que foi realizada uma vez por meio de meio ambiente/objeto. No tempo de execução, o pedido de visibilidade dependente da visualização foi gerado atravessando a árvore.
• A tese de doutorado de Naylor de 1981 forneceu um desenvolvimento completo de ambas as árvores de BSP e uma abordagem de grafo-teórico usando componentes fortemente conectados para visibilidade pré-computante, bem como a conexão entre os dois métodos. As árvores de BSP como uma estrutura de pesquisa espacial independente de dimensão foram enfatizadas, com aplicações para determinação de superfície visível. A tese também incluiu os primeiros dados empíricos demonstrando que o tamanho da árvore e o número de novos polígonos eram razoáveis (usando um modelo do ônibus espacial).
• 1983 Fuchs et al. descreveu uma implementação de micro-código do algoritmo de árvore BSP em um sistema de buffer de quadro Ikonas. Esta foi a primeira demonstração de determinação de superfície visível em tempo real usando árvores BSP.
• 1987 Thibault e Naylor descreveram como poliedros arbitrários podem ser representados usando uma árvore BSP em oposição ao b-rep tradicional (representação abundante). Isso forneceu uma representação sólida versus uma representação baseada na superfície. As operações definidas em poliedros foram descritas usando uma ferramenta, permitindo a geometria sólida construtiva (CSG) em tempo real. Este foi o precursor do projeto de nível BSP usando "brushes", introduzido no editor Quake e pego no Editor Unreal.
• 1990 Naylor, Amanatides e Thibault forneceram um algoritmo para fundir duas árvores BSP para formar uma nova árvore BSP das duas árvores originais. Isso fornece muitos benefícios, incluindo a combinação de objetos em movimento representados por árvores BSP com um ambiente estático (também representado por uma árvore BSP), operações CSG muito eficientes em poliedros, detecção de colisões exatas em O(log n * log n), e ordenação adequada de superfícies transparentes contidas em dois objetos interpenetrantes (foi usado para um efeito de visão de raios X).
• 1990 Teller e Séquin propuseram a geração off-line de conjuntos potencialmente visíveis para acelerar a determinação da superfície visível em ambientes 2D ortogonais.
• 1991 Gordon e Chen [CHEN91] descreveram um método eficiente de realização de renderização frontal a posterior de uma árvore BSP, em vez da abordagem tradicional de back-to-front. Eles utilizaram uma estrutura de dados especial para gravar, eficientemente, partes da tela que foram desenhadas, e aqueles ainda a serem renderizados. Este algoritmo, juntamente com a descrição de BSP Trees no computador padrão gráfico livro do dia (Gráficos de computador: Princípios e Prática) foi usado por John Carmack na criação de Doom (jogo de vídeo).
• 1992 A tese de doutorado de Teller descreveu a geração eficiente de conjuntos potencialmente visíveis como uma etapa de pré-processamento para acelerar a determinação de superfície visível em tempo real em ambientes poligonais 3D arbitrários. Isto foi usado em Quake e contribuiu significativamente para o desempenho desse jogo.
• 1993 Naylor respondeu à pergunta do que caracteriza uma boa árvore BSP. Ele usou modelos de caso esperados (em vez de análise de pior caso) para medir matematicamente o custo esperado de pesquisa de uma árvore e usou essa medida para construir boas árvores de BSP. Intuitivamente, a árvore representa um objeto de uma forma multi-resolução (mais exatamente como uma árvore de aproximações). Paralelos com códigos Huffman e árvores de busca binárias probabilísticas são desenhados.
• 1993 Tese de Ph.D. de Hayder Radha descrito (natural) métodos de representação de imagem usando árvores BSP. Isso inclui o desenvolvimento de uma estrutura de construção de árvore BSP ideal para qualquer imagem de entrada arbitrária. Esta estrutura é baseada em uma nova transformação de imagem, conhecida como a linha de particionamento Least-Square-Error (LSE) (LPE). A tese de H. Radha também desenvolveu uma estrutura de compressão de imagem de distorção de taxa ideal (RD) e abordagens de manipulação de imagem usando árvores BSP.

Visão geral

O particionamento de espaço binário é um processo genérico de divisão recursiva de uma cena em duas até que o particionamento satisfaça um ou mais requisitos. Pode ser visto como uma generalização de outras estruturas de árvores espaciais, como árvores k-d e quadtrees, onde os hiperplanos que particionam o espaço podem ter qualquer orientação, em vez de estarem alinhados com os eixos de coordenadas como estão em k-d árvores ou quadtrees. Quando usados em computação gráfica para renderizar cenas compostas por polígonos planares, os planos de particionamento são frequentemente escolhidos para coincidir com os planos definidos pelos polígonos na cena.

A escolha específica do plano de particionamento e o critério para encerrar o processo de particionamento varia dependendo da finalidade da árvore BSP. Por exemplo, na renderização de computação gráfica, a cena é dividida até que cada nó da árvore BSP contenha apenas polígonos que podem ser renderizados em ordem arbitrária. Quando a seleção da face posterior é usada, cada nó contém, portanto, um conjunto convexo de polígonos, enquanto ao renderizar polígonos de dupla face, cada nó da árvore BSP contém apenas polígonos em um único plano. Na detecção de colisão ou traçado de raios, uma cena pode ser dividida em primitivas nas quais os testes de colisão ou intersecção de raios são simples.

O particionamento de espaço binário surgiu da computação gráfica que precisava desenhar rapidamente cenas tridimensionais compostas de polígonos. Uma forma simples de desenhar tais cenas é o algoritmo do pintor, que produz polígonos em ordem de distância do observador, de trás para frente, pintando sobre o fundo e polígonos anteriores com cada objeto mais próximo. Esta abordagem tem duas desvantagens: o tempo necessário para classificar os polígonos na ordem de trás para frente e a possibilidade de erros na sobreposição de polígonos. Fuchs e co-autores mostraram que a construção de uma árvore BSP resolveu ambos os problemas, fornecendo um método rápido de classificação de polígonos em relação a um determinado ponto de vista (linear no número de polígonos na cena) e subdividindo polígonos sobrepostos para evitar erros que pode ocorrer com o algoritmo do pintor. Uma desvantagem do particionamento de espaço binário é que a geração de uma árvore BSP pode ser demorada. Normalmente, ele é executado uma vez na geometria estática, como uma etapa de pré-cálculo, antes da renderização ou de outras operações em tempo real em uma cena. O custo de construção de uma árvore BSP torna difícil e ineficiente implementar diretamente objetos móveis em uma árvore.

Geração

O uso canônico de uma árvore BSP é para renderizar polígonos (que são frente e verso, ou seja, sem seleção da face posterior) com o algoritmo do pintor. Cada polígono é designado com um lado frontal e um lado traseiro que podem ser escolhidos arbitrariamente e afetam apenas a estrutura da árvore, mas não o resultado desejado. Essa árvore é construída a partir de uma lista não ordenada de todos os polígonos de uma cena. O algoritmo recursivo para construção de uma árvore BSP a partir dessa lista de polígonos é:

1. Escolha um polígono P da lista.
2. Faça um nó N na árvore BSP, e adicionar P para a lista de polígonos naquele nó.
3. Para um outro polígono na lista:
   1. Se esse polígono estiver totalmente em frente ao avião que contém P, mova esse polígono para a lista de nós na frente de P.
   2. Se esse polígono estiver completamente atrás do avião que contém P, mover esse polígono para a lista de nós atrás P.
   3. Se esse polígono é intersetado pelo avião que contém P, dividi-lo em dois polígonos e movê-los para as respectivas listas de polígonos atrás e na frente de P.
   4. Se esse polígono estiver no avião que contém P, adicioná-lo à lista de polígonos no nó N.
4. Aplicar este algoritmo na lista de polígonos na frente de P.
5. Aplicar este algoritmo na lista de polígonos atrás P.

O diagrama a seguir ilustra o uso deste algoritmo na conversão de uma lista de linhas ou polígonos em uma árvore BSP. Em cada uma das oito etapas (i.-viii.), o algoritmo acima é aplicado a uma lista de linhas e um novo nó é adicionado à árvore.

	Comece com uma lista de linhas, (ou em 3D, polígonos) formando a cena. Nos diagramas de árvores, as listas são denotadas por retângulos arredondados e nós na árvore BSP por círculos. No diagrama espacial das linhas, a direção escolhida para ser a "fronta" de uma linha é denotada por uma seta.
Eu.	Seguindo os passos do algoritmo acima, Nós escolhemos uma linha, A, da lista e,... ...deve-o a um nó. Dividimos as linhas restantes na lista para aqueles na frente de A (isto é, B2, C2, D2), e aqueles atrás (B1, C1, D1). Primeiro processamos as linhas na frente de A (em passos ii-v),... ...seguido por aqueles por trás (em passos vi–vii).
Ii.	Agora aplicamos o algoritmo à lista de linhas na frente de A (contendo B2, C2, D2). Escolhemos uma linha, B2, adicioná-la a um nó e dividir o resto da lista nas linhas que estão na frente de B2 (D2), e aqueles que estão por trás dele (C2, D3).
iii.	Escolha uma linha, D2, da lista de linhas em frente a B2 e A. É a única linha na lista, então depois de a adicionar a um nó, nada mais precisa ser feito.
iv.	Nós somos feitos com as linhas na frente de B2, então considere as linhas por trás B2 (C2 e D3). Escolha um destes (C2), adicione-o a um nó, e coloque a outra linha na lista (D3) na lista de linhas na frente de C2.
V.	Agora veja a lista de linhas na frente de C2. Há apenas uma linha (D3), então adicione isso a um nó e continue.
Vi.	Agora adicionamos todas as linhas na frente de A para a árvore BSP, então agora começamos na lista de linhas atrás de A. Escolhendo uma linha (B1) desta lista, acrescentamos B1 a um nó e dividimos o restante da lista em linhas na frente de B1 (i.e. D1), e linhas atrás de B1 (i.e. C1).
Vii.	Processando primeiro a lista de linhas na frente de B1, D1 é a única linha nesta lista, então adicione isso a um nó e continue.
Viii.	Olhando ao lado da lista de linhas atrás de B1, a única linha nesta lista é C1, então adicione isso a um nó, e a árvore BSP está completa.

O número final de polígonos ou linhas em uma árvore geralmente é maior (às vezes muito maior) que a lista original, pois as linhas ou polígonos que cruzam o plano de particionamento devem ser divididos em dois. É desejável minimizar este aumento, mas também manter um equilíbrio razoável na árvore final. A escolha de qual polígono ou linha será usado como plano de particionamento (na etapa 1 do algoritmo) é, portanto, importante na criação de uma árvore BSP eficiente.

Travessia

Uma árvore BSP é percorrida em um tempo linear, em uma ordem determinada pela função específica da árvore. Novamente, usando o exemplo de renderização de polígonos de dois lados usando o algoritmo do pintor, para desenhar um polígono P corretamente, é necessário que todos os polígonos atrás do plano P estejam em ser desenhado primeiro, depois o polígono P e, finalmente, os polígonos na frente de P. Se esta ordem de desenho for satisfeita para todos os polígonos em uma cena, então toda a cena será renderizada na ordem correta. Este procedimento pode ser implementado percorrendo recursivamente uma árvore BSP usando o seguinte algoritmo. A partir de um determinado local de visualização V, para renderizar uma árvore BSP,

1. Se o nó atual é um nó de folha, torne os polígonos no nó atual.
2. Caso contrário, se o local de visualização V está em frente ao nó atual:
   1. Render a árvore BSP criança contendo polígonos atrás do nó atual
   2. Render os polígonos no nó atual
   3. Render a árvore BSP criança que contém polígonos na frente do nó atual
3. Caso contrário, se o local de visualização V está por trás do nó atual:
   1. Render a árvore BSP criança que contém polígonos na frente do nó atual
   2. Render os polígonos no nó atual
   3. Render a árvore BSP criança contendo polígonos atrás do nó atual
4. Caso contrário, o local de visualização V deve estar exatamente no plano associado ao nó atual. Então:
   1. Render a árvore BSP criança que contém polígonos na frente do nó atual
   2. Render a árvore BSP criança contendo polígonos atrás do nó atual

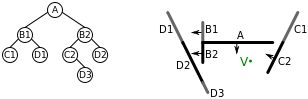
Aplicar este algoritmo recursivamente à árvore BSP gerada acima resulta nas seguintes etapas:

• O algoritmo é aplicado pela primeira vez ao nó raiz da árvore, nó A. V está em frente ao nó A, então aplicamos o algoritmo primeiro à árvore BSP criança que contém polígonos atrás A
  • Esta árvore tem nó raiz B1. V está por trás B1 assim primeiro, aplicamos o algoritmo à árvore BSP criança que contém polígonos na frente de B1:
    • Esta árvore é apenas o nó da folha D1, então o polígono D1 é renderizado.
  • Nós então renderizamos o polígono B1.
  • Em seguida, aplicamos o algoritmo à árvore BSP criança contendo polígonos atrás B1:
    • Esta árvore é apenas o nó da folha C1, então o polígono C1 é renderizado.
• Então desenhamos os polígonos de A
• Em seguida, aplicamos o algoritmo à árvore BSP criança contendo polígonos na frente de A
  • Esta árvore tem nó raiz B2. V está por trás B2 assim primeiro, aplicamos o algoritmo à árvore BSP criança que contém polígonos na frente de B2:
    • Esta árvore é apenas o nó da folha D2, então o polígono D2 é renderizado.
  • Nós então renderizamos o polígono B2.
  • Em seguida, aplicamos o algoritmo à árvore BSP criança contendo polígonos atrás B2:
    • Esta árvore tem nó raiz C2. V está em frente de C2 assim primeiro, aplicaríamos o algoritmo à árvore BSP criança que contém polígonos atrás C2. No entanto, não existe tal árvore, por isso continuamos.
    • Tornamos o polígono C2.
    • Aplicamos o algoritmo à árvore BSP da criança que contém polígonos na frente de C2
      • Esta árvore é apenas o nó da folha D3, então o polígono D3 é renderizado.

A árvore é percorrida em tempo linear e renderiza os polígonos em uma ordem de longe para perto (D1, B1, C1, A, D2, B2, C2, D3) adequado para o pintor&# algoritmo de 39;

Aplicativo

As árvores BSP são frequentemente usadas em videogames 3D, principalmente em jogos de tiro em primeira pessoa e em ambientes internos. Os motores de jogo que usam árvores BSP incluem os motores Doom (id Tech 1), Quake (variante id Tech 2), GoldSrc e Source. Neles, árvores BSP contendo a geometria estática de uma cena são frequentemente usadas junto com um buffer Z, para mesclar corretamente objetos móveis, como portas e personagens, na cena de fundo. Embora o particionamento de espaço binário forneça uma maneira conveniente de armazenar e recuperar informações espaciais sobre polígonos em uma cena, ele não resolve o problema da determinação da superfície visível. No entanto, árvores BSP foram aplicadas à compressão de imagens.

Referências adicionais