Número Mach
Mach number (M ou Ma) (Alemão: [max]) é uma quantidade adimensional em dinâmica de fluidos que representa a razão da velocidade do fluxo após um limite para a velocidade local de som. É nomeado após o físico e filósofo austríaco Ernst Mach.
- M= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =uc,{displaystyle mathrm {M} ={frac {u}{c}},}
onde:
- M é o número local de Mach,
- u é a velocidade de fluxo local com relação aos limites (tanto interno, como um objeto imerso no fluxo, ou externo, como um canal), e
- c é a velocidade do som no meio, que no ar varia com a raiz quadrada da temperatura termodinâmica.
Por definição, em Mach 1, a velocidade do fluxo local u é igual à velocidade do som. Em Mach 0,65, u é 65% da velocidade do som (subsônico) e, em Mach 1,35, u é 35% mais rápido que o velocidade do som (supersônico). Os pilotos de veículos aeroespaciais de alta altitude usam o número Mach de voo para expressar a velocidade real de um veículo, mas o campo de fluxo em torno de um veículo varia em três dimensões, com variações correspondentes no número Mach local.
A velocidade local do som e, portanto, o número de Mach, depende da temperatura do gás circundante. O número de Mach é usado principalmente para determinar a aproximação com a qual um fluxo pode ser tratado como um fluxo incompressível. O meio pode ser um gás ou um líquido. A fronteira pode estar viajando no meio, ou pode estar estacionária enquanto o meio flui ao longo dela, ou ambos podem estar se movendo, com velocidades diferentes: o que importa é a velocidade relativa entre si. O limite pode ser o limite de um objeto imerso no meio, ou de um canal como um bocal, difusor ou túnel de vento canalizando o meio. Como o número de Mach é definido como a razão entre duas velocidades, é um número adimensional. Se M < 0,2–0,3 e o fluxo for quase estacionário e isotérmico, os efeitos de compressibilidade serão pequenos e equações simplificadas de fluxo incompressível podem ser usadas.
Etimologia
O número Mach recebe o nome do físico e filósofo Ernst Mach, e é uma designação proposta pelo engenheiro aeronáutico Jakob Ackeret em 1929. Como o número Mach é uma quantidade adimensional e não uma unidade de medida, o número vem após a unidade; o segundo número de Mach é Mach 2 em vez de 2 Mach (ou Machs). Isso lembra um pouco a unidade de som oceânico moderno marca (um sinônimo de braça), que também era a primeira unidade e pode ter influenciado o uso do termo Mach. Na década anterior ao vôo humano mais rápido que o som, os engenheiros aeronáuticos se referiam à velocidade do som como número de Mach, nunca Mach 1.
Visão geral

O número de Mach é uma medida das características de compressibilidade do fluxo de fluido: o fluido (ar) se comporta sob a influência da compressibilidade de maneira semelhante em um determinado número de Mach, independentemente de outras variáveis. Conforme modelado na Atmosfera Padrão Internacional, ar seco ao nível médio do mar, temperatura padrão de 15 °C (59 °F), a velocidade do som é de 340,3 metros por segundo (1.116,5 pés/s; 761,23 mph; 1.225,1 km/h; 661,49 kn). A velocidade do som não é uma constante; em um gás, aumenta proporcionalmente à raiz quadrada da temperatura absoluta e, como a temperatura atmosférica geralmente diminui com o aumento da altitude entre o nível do mar e 11.000 metros (36.089 pés), a velocidade do som também diminui. Por exemplo, o modelo de atmosfera padrão reduz a temperatura para −56,5 °C (−69,7 °F) a 11.000 metros (36.089 pés) de altitude, com uma velocidade de som correspondente (Mach 1) de 295,0 metros por segundo (967,8 ft/s; 659,9 mph; 1.062 km/h; 573,4 kn), 86,7% do valor do nível do mar.
Aparência na equação de continuidade
Como uma medida de compressibilidade de fluxo, o número de Mach pode ser derivado de uma escala apropriada da equação de continuidade. A equação de continuidade completa para um fluxo de fluido geral é:
Classificação dos regimes Mach
Enquanto os termos subsônico e supersônico, no sentido mais puro, referem-se a velocidades abaixo e acima da velocidade local do som, respectivamente, os aerodinamicistas costumam usar os mesmos termos para falar sobre faixas particulares de valores de Mach. Isso ocorre devido à presença de um regime transônico em torno do voo (corrente livre) M = 1 onde as aproximações das equações de Navier-Stokes usadas para projeto subsônico não mais se aplicam; a explicação mais simples é que o fluxo ao redor de uma fuselagem localmente começa a exceder M = 1, mesmo que o número de Mach do fluxo livre esteja abaixo desse valor.
Enquanto isso, o regime supersônico é geralmente usado para falar sobre o conjunto de números de Mach para os quais a teoria linearizada pode ser usada, onde, por exemplo, o fluxo (de ar) não reage quimicamente e onde o calor -a transferência entre o ar e o veículo pode ser razoavelmente negligenciada nos cálculos.
Na tabela a seguir, os regimes ou faixas de valores de Mach são referidos, e não os significados puros das palavras subsônico e supersônico.
Geralmente, a NASA define hipersônico alto como qualquer número de Mach de 10 a 25, e velocidades de reentrada como qualquer coisa maior que Mach 25. Aeronaves operando neste regime incluem o ônibus espacial e vários aviões espaciais em desenvolvimento.
| Regime | Velocidade de voo | Características gerais do plano | ||||
|---|---|---|---|---|---|---|
| (Mach) | (knots) | (mph) | (km/h) | (m/s) | ||
| Subsónico | <0,8 | <530 | <609 | <980 | <273 | Na maioria das vezes, aeronaves turbofan com motor de hélice e comerciais com asas de elevado aspecto-ratio (slender) e características arredondadas como o nariz e as bordas principais.
A faixa de velocidade subsônica é aquela faixa de velocidades dentro da qual, todo o fluxo de ar sobre uma aeronave é inferior a Mach 1. O número crítico de Mach (Mcrit) é o menor número de fluxo livre Mach no qual o fluxo de ar sobre qualquer parte da aeronave atinge primeiro Mach 1. Assim, a faixa de velocidade subsônica inclui todas as velocidades que são menos do que Mcrit. |
| Transcrição | 0,8–1.2 | 530–794 | 609–914 | 980–1.470 | 273–409 | As aeronaves transônicas quase sempre varreram asas, causando o atraso da drag-divergence, e muitas vezes apresentam um design que adere aos princípios da regra da Área Whitcomb.
A faixa de velocidade transônica é aquela faixa de velocidades dentro das quais o fluxo de ar sobre diferentes partes de uma aeronave é entre subsônico e supersônico. Assim, o regime de voo de Mcrit até Mach 1.3 é chamado de gama transônica. |
| Supersonic | 1.2–5.0 | 794–3,308 | 915–3,806 | 1,470–6,126 | 410–1,702 | A faixa de velocidade supersônica é a faixa de velocidades dentro das quais todo o fluxo de ar sobre uma aeronave é supersônico (mais do que Mach 1). Mas o fluxo de ar que encontra as bordas principais é inicialmente desacelerado, então a velocidade de fluxo livre deve ser ligeiramente maior do que Mach 1 para garantir que todo o fluxo sobre a aeronave é supersônico. É comumente aceito que a faixa de velocidade supersônica começa em uma velocidade de fluxo livre maior do que Mach 1.3.
Aeronave projetada para voar em velocidades supersônicas mostram grandes diferenças em seu design aerodinâmico por causa das diferenças radicais no comportamento dos fluxos acima de Mach 1. As bordas afiadas, as secções de aerofólio finas e todo-movimento de cauda / canards são comuns. As aeronaves de combate modernas devem comprometer para manter o manuseio de baixa velocidade; os projetos supersônicos "verdadeiros" incluem o F-104 Starfighter, MiG-31, North American XB-70 Valkyrie, SR-71 Blackbird e BAC/Aérospatiale Concorde. |
| Hypersonic | 5.0–10.0 | 3,308–6,615 | 3,806–7,680 | 6,126–12,251 | 1,702–3,403 | O X-15, em Mach 6.72 é uma das aeronaves tripuladas mais rápidas. Além disso, a pele de níquel-titânio refrigerada; altamente integrada (devido à dominação de efeitos de interferência: o comportamento não linear significa que a superposição de resultados para componentes separados é inválida), asas pequenas, como as do Waverider Mach 5 X-51A. |
| Alta-hipessoal | 10.0–25.0 | 6,615–16,537 | 7,680–19,031 | 12,251–30,626 | 3,403–8,508 | A NASA X-43, em Mach 9.6 é uma das aeronaves mais rápidas. O controle térmico torna-se uma consideração de design dominante. A estrutura deve ser projetada para operar quente, ou ser protegida por telhas de silicato especiais ou semelhantes. O fluxo de reação química também pode causar corrosão da pele do veículo, com oxigênio livre-atômico com fluxos de alta velocidade. Projetos hipersônicos são muitas vezes forçados em configurações desfocadas por causa do aquecimento aerodinâmico subindo com um raio reduzido de curvatura. |
| Velocidades de reentrada | >) | > 16,537 | >19,031 | > 30,626 | >8.508 | Escudo de calor ablativo; pequenas ou nenhuma asas; forma desfocada. A Avangard da Rússia (veículo de deslizamento hipessoal) é reivindicada para chegar até Mach 27. |
Fluxo de alta velocidade em torno de objetos
O voo pode ser classificado em seis categorias:
| Regime | Subsónico | Transcrição | Velocidade do som | Supersonic | Hypersonic | Hipervelocidade |
|---|---|---|---|---|---|---|
| Mach | <0,8 | 0,8–1.2 | 1.0. | 1.2–5.0 | 5.0–10.0 | >8.8 |
Para comparação: a velocidade necessária para a órbita baixa da Terra é de aproximadamente 7,5 km/s = Mach 25,4 no ar em grandes altitudes.
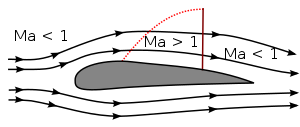
Em velocidades transônicas, o campo de fluxo ao redor do objeto inclui partes sub e supersônicas. O período transônico começa quando as primeiras zonas de M > 1 fluxo aparece ao redor do objeto. No caso de um aerofólio (como a asa de uma aeronave), isso geralmente acontece acima da asa. O fluxo supersônico pode desacelerar de volta ao subsônico apenas em um choque normal; isso normalmente acontece antes da borda de fuga. (Fig.1a)
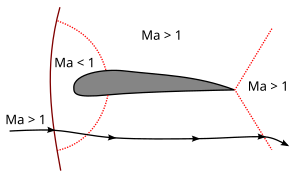
À medida que a velocidade aumenta, a zona de M > 1 o fluxo aumenta em direção às bordas de ataque e fuga. Quando M = 1 é alcançado e ultrapassado, o choque normal atinge o bordo de fuga e se torna um choque oblíquo fraco: o fluxo desacelera sobre o choque, mas permanece supersônico. Um choque normal é criado à frente do objeto, e a única zona subsônica no campo de fluxo é uma pequena área ao redor da borda principal do objeto. (Fig.1b)
 |  |
| (a) | (b) |
Fig. 1. Número Mach no fluxo de ar transônico em torno de um aerofólio; M < 1 (a) e M > 1 (b).
Quando uma aeronave excede Mach 1 (ou seja, a barreira do som), uma grande diferença de pressão é criada logo à frente da aeronave. Essa diferença abrupta de pressão, chamada de onda de choque, se espalha para trás e para fora da aeronave em forma de cone (o chamado cone de Mach). É essa onda de choque que causa o estrondo sônico ouvido quando uma aeronave em movimento rápido passa por cima. Uma pessoa dentro da aeronave não ouvirá isso. Quanto maior a velocidade, mais estreito o cone; logo acima de M = 1 dificilmente é um cone, mas mais próximo de um plano levemente côncavo.
Em velocidade totalmente supersônica, a onda de choque começa a tomar sua forma de cone e o fluxo é completamente supersônico ou (no caso de um objeto pontiagudo), apenas uma pequena área de fluxo subsônico permanece entre o nariz do objeto e a onda de choque que cria à sua frente. (No caso de um objeto pontiagudo, não há ar entre o nariz e a onda de choque: a onda de choque começa no nariz.)
À medida que o número Mach aumenta, também aumenta a força da onda de choque e o cone Mach torna-se cada vez mais estreito. À medida que o fluxo de fluido atravessa a onda de choque, sua velocidade é reduzida e a temperatura, a pressão e a densidade aumentam. Quanto mais forte o choque, maiores as mudanças. Em números de Mach altos o suficiente, a temperatura aumenta tanto durante o choque que a ionização e a dissociação das moléculas de gás por trás da onda de choque começam. Esses fluxos são chamados hipersônicos.
É claro que qualquer objeto viajando em velocidades hipersônicas também será exposto às mesmas temperaturas extremas que o gás por trás da onda de choque do nariz e, portanto, a escolha de materiais resistentes ao calor torna-se importante.
Fluxo de alta velocidade em um canal
À medida que um fluxo em um canal se torna supersônico, ocorre uma mudança significativa. A conservação da taxa de fluxo de massa leva a esperar que a contração do canal de fluxo aumente a velocidade do fluxo (ou seja, tornar o canal mais estreito resulta em fluxo de ar mais rápido) e em velocidades subsônicas isso é verdade. No entanto, uma vez que o fluxo se torna supersônico, a relação entre área de fluxo e velocidade é invertida: expandir o canal na verdade aumenta a velocidade.
O resultado óbvio é que, para acelerar um fluxo para supersônico, é necessário um bocal convergente-divergente, onde a seção convergente acelera o fluxo para velocidades sônicas e a seção divergente continua a aceleração. Esses bicos são chamados de bicos de Laval e, em casos extremos, são capazes de atingir velocidades hipersônicas (Mach 13 (15.900 km/h; 9.900 mph) a 20 °C).
Um Machímetro de aeronave ou sistema eletrônico de informações de voo (EFIS) pode exibir o número Mach derivado da pressão de estagnação (tubo de pitot) e da pressão estática.
Cálculo
Quando a velocidade do som é conhecida, o número Mach no qual uma aeronave está voando pode ser calculado por
- M= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =uc{displaystyle mathrm Não. Não.
onde:
- M é o número Mach
- u é a velocidade da aeronave em movimento e
- c é a velocidade do som na altitude dada (mais apropriada temperatura)
e a velocidade do som varia com a temperatura termodinâmica como:
- c= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =γ γ )) R∗ ∗ )) T,{displaystyle c={sqrt {gamma cdot R_{*}cdot T}},
onde:
- γ γ {displaystyle gamma ,} é a proporção de calor específico de um gás a uma pressão constante para aquecer em um volume constante (1,4 para o ar)
- R∗ ∗ Não. R_{*}} é a constante de gás específica para o ar.
- T,Não. T, é a temperatura do ar estático.
Se a velocidade do som não for conhecida, o número de Mach pode ser determinado medindo as várias pressões do ar (estática e dinâmica) e usando a seguinte fórmula derivada da equação de Bernoulli para números de Mach menores que 1,0. Assumindo que o ar é um gás ideal, a fórmula para calcular o número de Mach em um fluxo compressível subsônico é:
- M= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2γ γ - Sim. - Sim. 1Não.(qcp+1)γ γ - Sim. - Sim. 1γ γ - Sim. - Sim. 1]{displaystyle mathrm {M} ={sqrt {{frac {2}{gamma -1}}left[left({frac {q_{c}}{p}}+1right)^{frac - Sim. }}-1right],}
onde:
- qc é pressão de impacto (pressão dinâmica) e
- p é pressão estática
- γ γ {displaystyle gamma ,} é a proporção de calor específico de um gás a uma pressão constante para aquecer em um volume constante (1,4 para o ar)
A fórmula para calcular o número de Mach em um fluxo compressível supersônico é derivada da equação pitot supersônica de Rayleigh:
- p)p= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Não.γ γ +12M2]γ γ γ γ - Sim. - Sim. 1)) Não.γ γ +11- Sim. - Sim. γ γ +2γ γ M2]1γ γ - Sim. - Sim. 1Não. {p_{t}}{p}}=left Não. {gamma +1}{2}}mathrm {M} ^{2}right]^{frac {gamma }{gamma -1}}cdot left[{frac {gamma] +1 +2gamma ,mathrm {M} ^{2}}}right]^{frac {1}{gamma - Sim.
Calculando o número de Mach a partir da pressão do tubo pitot
O número Mach é uma função da temperatura e da velocidade real. Os instrumentos de voo da aeronave, no entanto, operam usando o diferencial de pressão para calcular o número de Mach, não a temperatura.
Assumindo que o ar é um gás ideal, a fórmula para calcular o número de Mach em um fluxo compressível subsônico é encontrada na equação de Bernoulli para M < 1 (acima):
- M= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =5Não.(qcp+1)27- Sim. - Sim. 1]{displaystyle mathrm {M} ={sqrt {5left[left({frac {q_{c}}{p}}+1right)^{frac {2}{7}}-1right]}}, ?
A fórmula para calcular o número de Mach em um fluxo compressível supersônico pode ser encontrada na equação pitot supersônica de Rayleigh (acima) usando parâmetros para o ar:
- M? ? 0,8128485(qcp+1)(1- Sim. - Sim. 17M2)2.5.{displaystyle mathrm {M} approx 0.88128485{sqrt {left({frac {q_{c}}{p}}+1right)left(1-{frac {1}{7,mathrm {M} ^{2}}}right)^{2.5}}
onde:
- qc é a pressão dinâmica medida por trás de um choque normal.
Como pode ser visto, M aparece em ambos os lados da equação e, para fins práticos, um algoritmo de localização de raízes deve ser usado para uma solução numérica (a solução da equação é uma raiz de um polinômio de 7ª ordem em M2 e, embora alguns deles possam ser resolvidos explicitamente, o teorema de Abel-Ruffini garante que não existe uma forma geral para as raízes desses polinômios). Primeiro é determinado se M é de fato maior que 1,0 calculando M a partir da equação subsônica. Se M for maior que 1,0 nesse ponto, então o valor de M da equação subsônica é usado como condição inicial para iteração de ponto fixo da equação supersônica, que geralmente converge muito rapidamente. Alternativamente, o método de Newton também pode ser usado.
Contenido relacionado
Álgebra de Banach
Teorema do ponto fixo de Brouwer
Antimatéria























![{displaystyle mathrm {M} ={sqrt {{frac {2}{gamma -1}}left[left({frac {q_{c}}{p}}+1right)^{frac {gamma -1}{gamma }}-1right]}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6cfb0b14f5726032a386928f8312725a3325c4c)
![{displaystyle {frac {p_{t}}{p}}=left[{frac {gamma +1}{2}}mathrm {M} ^{2}right]^{frac {gamma }{gamma -1}}cdot left[{frac {gamma +1}{1-gamma +2gamma ,mathrm {M} ^{2}}}right]^{frac {1}{gamma -1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e40925c7d73812aaeb7be0541fb045abfe268c54)
![{displaystyle mathrm {M} ={sqrt {5left[left({frac {q_{c}}{p}}+1right)^{frac {2}{7}}-1right]}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbbe331c3f8c63b187b0a3a3fc23580e4cb2ac55)
