Monoide
Na álgebra abstrata, um ramo da matemática, um monóide é um conjunto equipado com uma operação binária associativa e um elemento de identidade. Por exemplo, os inteiros não negativos com adição formam um monóide, sendo o elemento identidade 0.
Monóides são semigrupos com identidade. Tais estruturas algébricas ocorrem em vários ramos da matemática.
As funções de um conjunto em si formam um monóide em relação à composição da função. De forma mais geral, na teoria das categorias, os morfismos de um objeto para si mesmo formam um monóide e, inversamente, um monóide pode ser visto como uma categoria com um único objeto.
Na ciência da computação e programação de computadores, o conjunto de strings construídas a partir de um determinado conjunto de caracteres é um monóide livre. Monóides de transição e monóides sintáticos são usados na descrição de máquinas de estado finito. Monóides e histórico de rastreamento fornecem uma base para cálculos de processo e computação simultânea.
Na ciência da computação teórica, o estudo dos monóides é fundamental para a teoria dos autômatos (teoria de Krohn -Rhodes) e a teoria formal da linguagem (problema da altura das estrelas).
Veja semigrupo para a história do assunto e algumas outras propriedades gerais dos monóides.
Definição
um conjunto s equipado com uma operação binária s × s → s , que indicaremos •, é um monoid se satisfazer os dois axiomas a seguir:
- Associação
- Para todos um, b) e c em S, a equação (um • b)) c = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = um •b) • c) Detém.
- Elemento de identidade
- Existe um elemento e em S tal que para cada elemento um em S, a igualdade e • um = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = um e um • e = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = um Espera.
Em outras palavras, um monóide é um semigrupo com um elemento de identidade. Também pode ser pensado como um magma com associatividade e identidade. O elemento identidade de um monóide é único. Por esta razão, a identidade é considerada como uma constante, i. e. Operação 0-ária (ou nula). O monóide, portanto, é caracterizado pela especificação do triplo (S, • e).
Dependendo do contexto, o símbolo para a operação binária pode ser omitido, de modo que a operação seja denotada por justaposição; por exemplo, os axiomas monóides podem ser escritos (ab)c = a(bc) e ea = ae = a. Esta notação não implica que sejam números sendo multiplicados.
Um monóide no qual cada elemento tem um inverso é um grupo.
Estruturas monoides
Submonoides
Um submonoide de um monoide (M, •) é um subconjunto N de M que é fechado sob a operação monóide e contém o elemento de identidade e de M. Simbolicamente, N é um submonóide de M se N ⊆ M, x • y ∈ N sempre que x, y ∈ N e e ∈ N. Neste caso, N é um monoid sob a operação binária herdada de M.
Por outro lado, se N é um subconjunto de um monóide que é fechado sob a operação monoide e é um monoide para esta operação herdada, então N não é sempre um submonóide, pois os elementos de identidade podem diferir. Por exemplo, o conjunto singleton {0} é fechado sob multiplicação e não é um submonoide do monoide (multiplicativo) dos inteiros não negativos.
Geradores
Um subconjunto S de M é dito gerar M se o menor submonóide de M contendo S é M. Se existe um conjunto finito que gera M, então M é dito ser um monóide finitamente gerado.
Monóide comutativo
Um monóide cuja operação é comutativa é chamado de monóide comutativo (ou, menos comumente, um monóide abeliano). Monóides comutativos são frequentemente escritos de forma aditiva. Qualquer monóide comutativo é dotado de sua pré-ordenação algébrica ≤, definida por x ≤ y se existir z tal que x + z = y. Uma unidade de ordem de um monoide comutativo M é um elemento u de M tal que para qualquer elemento x de M, existe v no conjunto gerado por u tal que x ≤ v. Isso é frequentemente usado no caso de M ser o cone positivo de um grupo abeliano parcialmente ordenado G, caso em que dizemos que u é uma ordem -unidade de G.
Monóide parcialmente comutativo
Um monóide para o qual a operação é comutativa para alguns, mas não para todos os elementos é um monóide de traço; monóides de rastreamento comumente ocorrem na teoria da computação concorrente.
Exemplos
- Out of the 16 possible binary Boolean operators, four have a two-sided identity that is also commutative and associative. These four each make the set {False, True} a commutative monoid. Under the standard definitions, AND and XNOR have the identity True while XOR and OR have the identity False. The monoids from AND and OR are also idempotent while those from XOR and XNOR are not.
- The set of natural numbers N = { 0 , 1 , 2 , … } {displaystyle mathbb {N} ={0,1,2,ldots }} is a commutative monoid under addition (identity element 0) or multiplication (identity element 1). A submonoid of N under addition is called a numerical monoid.
- The set of positive integers N ∖ { 0 } {displaystyle mathbb {N} setminus {0}} is a commutative monoid under multiplication (identity element 1).
- Given a set A, the set of subsets of A is a commutative monoid under intersection (identity element is A itself).
- Given a set A, the set of subsets of A is a commutative monoid under union (identity element is the empty set).
- Generalizing the previous example, every bounded semilattice is an idempotent commutative monoid.
- In particular, any bounded lattice can be endowed with both a meet- and a join- monoid structure. The identity elements are the lattice's top and its bottom, respectively. Being lattices, Heyting algebras and Boolean algebras are endowed with these monoid structures.
- Every singleton set {x} closed under a binary operation • forms the trivial (one-element) monoid, which is also the trivial group.
- Every group is a monoid and every abelian group a commutative monoid.
- Any semigroup S may be turned into a monoid simply by adjoining an element e not in S and defining e • s = s = s • e for all s ∈ S. This conversion of any semigroup to the monoid is done by the free functor between the category of semigroups and the category of monoids.
- Thus, an idempotent monoid (sometimes known as find-first) may be formed by adjoining an identity element e to the left zero semigroup over a set S. The opposite monoid (sometimes called find-last) is formed from the right zero semigroup over S.
- Adjoin an identity e to the left-zero semigroup with two elements {lt, gt}. Then the resulting idempotent monoid {lt, e, gt} models the lexicographical order of a sequence given the orders of its elements, with e representing equality.
- Thus, an idempotent monoid (sometimes known as find-first) may be formed by adjoining an identity element e to the left zero semigroup over a set S. The opposite monoid (sometimes called find-last) is formed from the right zero semigroup over S.
- The underlying set of any ring, with addition or multiplication as the operation. (By definition, a ring has a multiplicative identity 1.)
- The integers, rational numbers, real numbers or complex numbers, with addition or multiplication as operation.
- The set of all n by n matrices over a given ring, with matrix addition or matrix multiplication as the operation.
- The set of all finite strings over some fixed alphabet Σ forms a monoid with string concatenation as the operation. The empty string serves as the identity element. This monoid is denoted Σ∗ and is called the free monoid over Σ. It is not commutative if Σ has at least two elements.
- Given any monoid M, the opposite monoid Mop has the same carrier set and identity element as M, and its operation is defined by x •op y = y • x. Any commutative monoid is the opposite monoid of itself.
- Given two sets M and N endowed with monoid structure (or, in general, any finite number of monoids, M1,..., Mk), their Cartesian product M × N is also a monoid (respectively, M1 × ⋯ × Mk). The associative operation and the identity element are defined pairwise.
- Fix a monoid M. The set of all functions from a given set to M is also a monoid. The identity element is a constant function mapping any value to the identity of M; the associative operation is defined pointwise.
- Fix a monoid M with the operation • and identity element e, and consider its power set P(M) consisting of all subsets of M. A binary operation for such subsets can be defined by S • T = { s • t: s ∈ S, t ∈ T }. This turns P(M) into a monoid with identity element {e}. In the same way the power set of a group G is a monoid under the product of group subsets.
- Let S be a set. The set of all functions S → S forms a monoid under function composition. The identity is just the identity function. It is also called the full transformation monoid of S. If S is finite with n elements, the monoid of functions on S is finite with nn elements.
- Generalizing the previous example, let C be a category and X an object of C. The set of all endomorphisms of X, denoted EndC(X), forms a monoid under composition of morphisms. For more on the relationship between category theory and monoids see below.
- The set of homeomorphism classes of compact surfaces with the connected sum. Its unit element is the class of the ordinary 2-sphere. Furthermore, if a denotes the class of the torus, and b denotes the class of the projective plane, then every element c of the monoid has a unique expression the form c = na + mb where n is a positive integer and m = 0, 1, or 2. We have 3b = a + b.
- Let
⟨
f
⟩
{displaystyle langle frangle }
be a cyclic monoid of order n, that is,
⟨
f
⟩
=
{
f
0
,
f
1
,
…
,
f
n
−
1
}
{displaystyle langle frangle =left{f^{0},f^{1},dotsf^{n-1}right}}
. Then
f
n
=
f
k
{displaystyle f^{n}=f^{k}}
for some
0
≤
k
<
n
{displaystyle 0leq k<n}
. In fact, each such k gives a distinct monoid of order n, and every cyclic monoid is isomorphic to one of these.
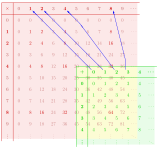
Moreover, f can be considered as a function on the points { 0 , 1 , 2 , … , n − 1 } {displaystyle {0,1,2,dotsn-1}} given byor, equivalently[ 0 1 2 ⋯ n − 2 n − 1 1 2 3 ⋯ n − 1 k ] {displaystyle {begin{bmatrix}0&1&2&cdots &n-2&n-1\1&2&3&cdots &n-1&kend{bmatrix}}}Multiplication of elements in ⟨ f ⟩ {displaystyle langle frangle } is then given by function composition. When k = 0 {displaystyle k=0} then the function f is a permutation of { 0 , 1 , 2 , … , n − 1 } , {displaystyle {0,1,2,dotsn-1},} and gives the unique cyclic group of order n.f ( i ) := { i + 1 , if 0 ≤ i < n − 1 k , if i = n − 1. {displaystyle f(i):={begin{cases}i+1,&{text{if }}0leq i<n-1\k,&{text{if }}i=n-1.end{cases}}}
Propriedades
Os axiomas monóides implicam que o elemento de identidade e é único: Se e e f são elementos de identidade de um monóide, então e = ef = f.
Produtos e poderes
Para cada inteiro nonnegative n, pode-se definir o produto pn= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =? ? Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1numEu...Não. p_{n}=textstyle prod _{i=1}^{n}a_{i}} de qualquer sequência (um1,...... ,umn)(a_{1},ldotsa_{n})} de n elementos de um monoide recursivamente: deixe p0 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = e e deixar pm = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = pm- Sim. • umm para 1 ≤ m ≤ n.
Como um caso especial, pode-se definir potências inteiras não negativas de um elemento x de um monóide: x0 = 1 e xn = xn−1 • x para n ≥ 1. Então xm+n = x m • xn para todos os m, n ≥ 0.
Elementos invertíveis
Um elemento x é chamado invertível se existir um elemento y tal que x • y = e e y • x = e. O elemento y é chamado de inverso de x. Os inversos, se existirem, são únicos: If y e z são inversas de x, então por associatividade y = ey = (zx)y = z(xy) = ze = z.
Se x for invertível, diga com y inverso, então pode-se definir potências negativas de x definindo x− n = yn para cada n ≥ 1; isso torna a equação xm+n = xm • xn para todos os m, n ∈ Z.
O conjunto de todos os elementos invertíveis em um monóide, junto com a operação •, forma um grupo.
Grupo Grothendieck
Nem todo monóide fica dentro de um grupo. Por exemplo, é perfeitamente possível ter um monóide no qual dois elementos a e b existe tal que a • b = a é válido mesmo que b não seja o elemento de identidade. Tal monóide não pode ser incorporado em um grupo, porque no grupo multiplicando ambos os lados com o inverso de a obteria b = e, o que não é verdade.
Um monoid (M, •) tem a propriedade de cancelamento (ou é cancelativo) se for para todos os estilos a, b e estilo c em M, a igualdade a • b = a • c implica b = c, e a igualdade b • a = c • a implica b = c.
Um monoide comutativo com a propriedade de cancelamento sempre pode ser incorporado em um grupo por meio da construção de grupo de Grothendieck. É assim que o grupo aditivo dos inteiros (um grupo com operação +) é construído a partir do monóide aditivo dos números naturais (um monóide comutativo com operação + e propriedade de cancelamento). No entanto, um monóide cancelativo não comutativo não precisa ser embutido em um grupo.
Se um monoid tem a propriedade de cancelamento e é finito, então é de fato um grupo.
Os elementos cancelativos à direita e à esquerda de um monóide, cada um por sua vez, formam um submonóide (ou seja, são fechados sob a operação e obviamente incluem a identidade). Isso significa que os elementos cancelativos de qualquer monóide comutativo podem ser estendidos a um grupo.
A propriedade cancelativa em um monóide não é necessária para realizar a construção de Grothendieck – a comutatividade é suficiente. No entanto, se um monóide comutativo não tiver a propriedade de cancelamento, o homomorfismo do monóide em seu grupo Grothendieck não é injetivo. Mais precisamente, se a • b = a • c, então b e c têm a mesma imagem no grupo Grothendieck, mesmo se b ≠ c. Em particular, se o monóide tiver um elemento absorvente, então seu grupo de Grothendieck é o grupo trivial.
Tipos de monóides
Um monóide inverso é um monóide onde para cada a em M, existe um único a−1 em M tal que a = a • a-1 • a e a-1 = a−1 • a • a−1. Se um monóide inverso é cancelativo, então é um grupo.
Na direção oposta, um monoide sem soma zero é um monoide escrito aditivamente no qual a + b = 0 implica que a = 0 e b = 0: equivalentemente, nenhum elemento diferente de zero tem um inverso aditivo.
Atos e operadores monoides
Seja M um monóide, com a operação binária denotada por • e o elemento identidade denotado por e. Então um M-act (esquerdo) (ou ato esquerdo sobre M) é um conjunto X junto com um operação ⋅: M × X → X que é compatível com a estrutura monóide da seguinte forma:
- para todos x em X: e) x = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = x;
- para todos um, b) em M e x em X: um ⋅ (b)) x) = (um • b)⋅) x.
Este é o análogo na teoria monóide de uma ação de grupo (esquerda). M-atos corretos são definidos de maneira semelhante. Um monóide com um ato também é conhecido como um monóide operador. Exemplos importantes incluem sistemas de transição de semi-autômatos. Um semigrupo de transformação pode ser transformado em um monóide de operador ao se juntar à transformação de identidade.
Homomorfismos monoides
Um homomorfismo entre dois monóides (M, ∗) e (N, •) é uma função f: M → N tal que
- f(x ∗ Sim.) = f(x) f(Sim.) para todos x, Sim. em M
- f(eM) = eN,
onde eM e eN são as identidades em M e N, respectivamente. Os homomorfismos monoides às vezes são simplesmente chamados de morfismos monoides.
Nem todo homomorfismo semigrupo entre monoides é um homomorfismo monoide, uma vez que pode não mapear a identidade da monoide alvo, mesmo que a identidade seja a identidade da imagem do homomorfismo. Por exemplo, considere MnNão. M_{n}}, o conjunto de classes de resíduos modulo nNão. equipado com multiplicação. Em particular, a classe de 1Não. 1 é a identidade. Função f:: M3→ → M6{displaystyle fcolon M_{3}to M_{6}} por f(k)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =3k(k)=3k} é um semigrupo homomorfismo como 3k)) 3Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =9kEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =3kEu...- Sim. em M6Não. M_{6}}. No entanto, f(1)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =3≠ ≠ 1{displaystyle f(1)=3neq 1}, assim um homomorfismo monoide é um homomorfismo semigrupo entre monoides que mapeia a identidade do primeiro monoide à identidade do segundo monoide e a última condição não pode ser omitida.
Por outro lado, um homomorfismo de semigrupo entre grupos é sempre um homomorfismo de grupo, pois necessariamente preserva a identidade (porque, em um grupo, a identidade é o único elemento tal que x ⋅ x = x).
Um homomorfismo monoide bijetivo é chamado de isomorfismo monoide. Dois monóides são ditos isomórficos se existe um isomorfismo monoide entre eles.
Apresentação equacional
Os monóides podem receber uma apresentação, da mesma forma que os grupos podem ser especificados por meio de uma apresentação de grupo. Faz-se isso especificando um conjunto de geradores Σ e um conjunto de relações no monóide livre Σ∗. Faz-se isso estendendo relações binárias (finitas) em Σ∗ para congruências monóides e, em seguida, construindo o monóide quociente, como acima.
Dada uma relação binária R ⊂ Σ∗ × Σ∗, define-se seu fechamento simétrico como R ∪ R−1. Isso pode ser estendido para uma relação simétrica E ⊂ Σ∗ × Σ∗ definindo x ~E y se e somente se x = sut e y = svt para algumas strings u, v, s, t ∈ Σ∗ com (u,v) ∈ R ∪ R−1. Finalmente, toma-se o fechamento reflexivo e transitivo de E, que é então uma congruência monóide.
Na situação típica, a relação R é simplesmente dado como um conjunto de equações, de modo que R= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(u1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =v1,⋯ ⋯ ,un= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =vn?Não. R={u_{1}=v_{1},cdotsu_{n}=v_{n}}}. Assim, por exemplo,
- ⟨ ⟨ p,q|pq= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1)) {displaystyle langle p,q,vert ;pq=1rangle }
é a apresentação equacional para o monóide bicíclico, e
- ⟨ ⟨ um,b)|umb)um= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =b)umum,b)b)um= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =b)umb))) {displaystyle langle a,b,vert ;aba=baa,bba=babrangle }
é o monóide plactico de grau 2 (tem ordem infinita). Elementos deste monóide plactico podem ser escritos como umEu...b)JJ(b)um)k{displaystyle a^{i}b^{j}(ba)^{k}} para inteiros Eu..., JJ, k, como as relações mostram que ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba ba comuta com ambos um e b).
Relação com a teoria da categoria
| Totalidade | Associação | Identidade | Invertido | Comutação | |
|---|---|---|---|---|---|
| Magma parcial | Sem necessidade | Sem necessidade | Sem necessidade | Sem necessidade | Sem necessidade |
| Semigroupoid | Sem necessidade | Requisitos | Sem necessidade | Sem necessidade | Sem necessidade |
| Categoria pequena | Sem necessidade | Requisitos | Requisitos | Sem necessidade | Sem necessidade |
| Grupo | Sem necessidade | Requisitos | Requisitos | Requisitos | Sem necessidade |
| Magma | Requisitos | Sem necessidade | Sem necessidade | Sem necessidade | Sem necessidade |
| Grupo Quasi | Requisitos | Sem necessidade | Sem necessidade | Requisitos | Sem necessidade |
| Magma unitário | Requisitos | Sem necessidade | Requisitos | Sem necessidade | Sem necessidade |
| Loop | Requisitos | Sem necessidade | Requisitos | Requisitos | Sem necessidade |
| Semigrupo | Requisitos | Requisitos | Sem necessidade | Sem necessidade | Sem necessidade |
| Monóide | Requisitos | Requisitos | Requisitos | Sem necessidade | Sem necessidade |
| Monoide comutativo | Requisitos | Requisitos | Requisitos | Sem necessidade | Requisitos |
| Grupo | Requisitos | Requisitos | Requisitos | Requisitos | Sem necessidade |
| Grupo Abeliano | Requisitos | Requisitos | Requisitos | Requisitos | Requisitos |
| ↑ O axioma de fechamento, usado por muitas fontes e definido de forma diferente, é equivalente. | |||||
Os monóides podem ser vistos como uma classe especial de categorias. De fato, os axiomas exigidos de uma operação monóide são exatamente os exigidos da composição de morfismos quando restritos ao conjunto de todos os morfismos cuja fonte e alvo é um dado objeto. Aquilo é,
- Um monoide é, essencialmente, a mesma coisa que uma categoria com um único objeto.
Mais precisamente, dado um monóide (M, •), pode-se construir uma pequena categoria com apenas um objeto e cujos morfismos são os elementos de M. A composição dos morfismos é dada pela operação monóide •.
Da mesma forma, homomorfismos monóides são apenas functores entre categorias de objetos únicos. Portanto, esta construção dá uma equivalência entre a categoria de (pequenos) monóides Mon e uma subcategoria completa da categoria de (pequenas) categorias Cat. Da mesma forma, a categoria de grupos é equivalente a outra subcategoria completa de Cat.
Nesse sentido, a teoria das categorias pode ser pensada como uma extensão do conceito de monóide. Muitas definições e teoremas sobre monóides podem ser generalizados para pequenas categorias com mais de um objeto. Por exemplo, um quociente de uma categoria com um objeto é apenas um monóide de quociente.
Monóides, assim como outras estruturas algébricas, também formam sua própria categoria, Mon, cujos objetos são monóides e cujos morfismos são homomorfismos de monóides.
Há também uma noção de objeto monóide que é uma definição abstrata do que é um monóide em uma categoria. Um objeto monoid em Set é apenas um monoid.
Monóides em ciência da computação
Na ciência da computação, muitos tipos de dados abstratos podem ser dotados de uma estrutura monóide. Em um padrão comum, uma sequência de elementos de um monóide é "dobrada" ou "acumulado" produzir um valor final. Por exemplo, muitos algoritmos iterativos precisam atualizar algum tipo de "total em execução" a cada iteração; esse padrão pode ser elegantemente expresso por uma operação monóide. Alternativamente, a associatividade de operações monóides garante que a operação possa ser paralelizada empregando uma soma de prefixo ou algoritmo semelhante, a fim de utilizar múltiplos núcleos ou processadores de forma eficiente.
Dada uma sequência de valores do tipo M com elemento de identidade ε ε - Sim. e operação associativa ? ? {displaystyle bullet }, o fold A operação é definida como segue:
- foEu...D:M∗ ∗ → → M= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu... Eu... ↦ ↦ (ε ε seEu... Eu... = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =nEu...Eu...m? ? foEu...DEu... Eu... ?seEu... Eu... = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =conSmEu... Eu... ?{displaystyle mathrm {fold}:M^{*}rightarrow M=ell mapsto - Sim. &{mbox{if }}ell =mathrm {nil} \mbullet mathrm {fold} ,ell '&{mbox{if }}ell =mathrm {cons} ,mell 'end{cases}}}
Além disso, qualquer estrutura de dados pode ser 'dobrada' de maneira semelhante, dada uma serialização de seus elementos. Por exemplo, o resultado de "dobrar" uma árvore binária pode diferir dependendo da travessia da árvore pré-ordem vs. pós-ordem.
MapReduce
Uma aplicação de monóides na ciência da computação é o chamado modelo de programação MapReduce (consulte Encoding Map-Reduce As A Monoid With Left Folding). MapReduce, em computação, consiste em duas ou três operações. Dado um conjunto de dados, "Mapa" consiste em mapear dados arbitrários para elementos de um monóide específico. "Reduzir" consiste em dobrar esses elementos, para que no final produzamos apenas um elemento.
Por exemplo, se tivermos um multiconjunto, em um programa ele é representado como um mapa dos elementos aos seus números. Os elementos são chamados de chaves neste caso. O número de chaves distintas pode ser muito grande e, nesse caso, o multiconjunto está sendo fragmentado. Para finalizar a redução adequadamente, o botão "Aleatório" estágio reagrupa os dados entre os nós. Se não precisarmos desta etapa, todo o Map/Reduce consiste em mapear e reduzir; ambas as operações são paralelizáveis, a primeira devido à sua natureza elementar, a última devido à associatividade do monóide.
Monóides completos
A monoideia completa é um monoide comutativo equipado com uma operação de soma infinitária Σ Σ Eu...Não. Sigma _{I}} para qualquer conjunto de índice Eu... tal que
- Gerenciamento Gerenciamento Eu...∈ ∈ ∅ ∅ mEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0;Gerenciamento Gerenciamento Eu...∈ ∈ (JJ?mEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =mJJ;Gerenciamento Gerenciamento Eu...∈ ∈ (JJ,k?mEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =mJJ+mkparaJJ≠ ≠ k{displaystyle sum _{iin emptyset }{m_{i}}=0;quad sum _{iin {j}}{m_{i}}=m_{j};quad sum _{iin {j,k}}{m_{i}}=m_{j}+m_{k}quad - Sim.
e
- Gerenciamento Gerenciamento JJ∈ ∈ JJGerenciamento Gerenciamento Eu...∈ ∈ Eu...JJmEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Gerenciamento Gerenciamento Eu...∈ ∈ Eu...mEu...se⋃ ⋃ JJ∈ ∈ JJEu...JJ= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Eu...eEu...JJ─ ─ Eu...JJ?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∅ ∅ paraJJ≠ ≠ JJ?{displaystyle sum _{jin J}{sum _{iin I_{j}}{m_{i}}}=sum _{iin I}m_{iquad} {text{ if }}bigcup _{jin J}I_{j}=I{text{ e }}I_{j}cap I_{j'}=emptyset quad {text{ para }}jneq j'}}.
Um monoide comutativo ordenado é um monoide comutativo M junto com uma ordenação parcial ≤ tal que a ≥ 0 para cada a ∈ M, e a ≤ b implica a + c ≤ b + c para todos os a, b, c ∈ M.
Um monóide contínuo é um monoide comutativo ordenado (M, ≤) no qual cada subconjunto direcionado tem pelo menos limite superior, e esses limites mínimos superiores são compatíveis com a operação monóide:
- um+Vamos.S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Vamos.(um+S){displaystyle a+sup S=sup(a+S)}
para cada a ∈ M e subconjunto direcionado S de M.
Se (M,≤) for um monóide contínuo, então para qualquer conjunto de índices I e coleção de elementos (ai)i ∈ I, pode-se definir
- Gerenciamento Gerenciamento Eu...umEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Vamos.finitoE? ? Eu...Gerenciamento Gerenciamento EumEu...,{displaystyle sum _{I}a_{i}=sup _{{text{finito }}Esubset I};sum _{E}a_{i},}
e M junto com esta operação de soma infinita é um monóide completo.
Contenido relacionado
Campo (matemática)
Homomorfismo de anel
Logaritmo natural
Matriz
Antiprisma