Máquina de estados finitos

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Modelo matemático da computação

Classes de automação

(Clique em cada camada recebe um artigo sobre esse assunto)

Uma máquina de estado finito (FSM) ou autômato de estado finito (FSA, plural: autômato), autômato finito, ou simplesmente uma máquina de estado, é um modelo matemático de computação. É uma máquina abstrata que pode estar exatamente em um de um número finito de estados a qualquer momento. O FSM pode mudar de um estado para outro em resposta a algumas entradas; a mudança de um estado para outro é chamada de transição. Uma FSM é definida por uma lista de seus estados, seu estado inicial e as entradas que disparam cada transição. As máquinas de estado finito são de dois tipos: máquinas de estado finito determinísticas e máquinas de estado finito não determinísticas. Uma máquina determinística de estado finito pode ser construída equivalente a qualquer não-determinística.

O comportamento das máquinas de estado pode ser observado em muitos dispositivos da sociedade moderna que executam uma sequência predeterminada de ações dependendo de uma sequência de eventos com os quais são apresentados. Exemplos simples são: vending machines, que dispensam produtos quando a combinação adequada de moedas é depositada; elevadores, cuja sequência de paradas é determinada pelos andares solicitados pelos usuários; semáforos, que mudam de sequência quando os carros estão esperando; fechaduras de combinação, que requerem a entrada de uma sequência de números na ordem correta.

A máquina de estado finito tem menos poder computacional do que alguns outros modelos de computação, como a máquina de Turing. A distinção de poder computacional significa que existem tarefas computacionais que uma máquina de Turing pode fazer, mas um FSM não pode. Isso ocorre porque a memória de um FSM é limitada pelo número de estados que possui. Uma máquina de estado finito tem o mesmo poder computacional que uma máquina de Turing que é restrita de forma que sua cabeça só pode executar "ler" operações, e sempre tem que se mover da esquerda para a direita. FSMs são estudados no campo mais geral da teoria dos autômatos.

Exemplo: catraca operada por moedas

Diagrama de estado para um giro

Um giro

Um exemplo de mecanismo simples que pode ser modelado por uma máquina de estado é uma catraca. A catraca, usada para controlar o acesso ao metrô e aos parques de diversões, é um portão com três braços giratórios na altura da cintura, um na entrada. Inicialmente os braços estão travados, bloqueando a entrada, impedindo a passagem dos frequentadores. Depositar uma moeda ou ficha em um slot na catraca destrava os braços, permitindo que um único cliente passe. Depois que o cliente passa, os braços são travados novamente até que outra moeda seja inserida.

Considerada uma máquina de estados, a catraca possui dois estados possíveis: Bloqueada e Desbloqueada. Existem duas entradas possíveis que afetam seu estado: colocar uma moeda no slot (coin) e empurrar o braço (push). No estado travado, empurrar o braço não tem efeito; não importa quantas vezes a entrada push seja dada, ela permanece no estado bloqueado. Colocar uma moeda – ou seja, dar à máquina uma entrada moeda – muda o estado de Bloqueado para Desbloqueado. No estado desbloqueado, colocar moedas adicionais não tem efeito; ou seja, fornecer entradas coin adicionais não altera o estado. No entanto, um cliente empurrando pelos braços, dando uma entrada empurrar, muda o estado de volta para Bloqueado.

A máquina de estado catraca pode ser representada por uma tabela de transição de estado, mostrando para cada estado possível, as transições entre eles (com base nas entradas dadas à máquina) e as saídas resultantes de cada entrada:

Estado actual	Entrada	Próximo Estado	Saída
Trancado.	moedas	Desbloqueado	Desbloqueia o tornez para que o cliente possa passar.
Trancado.	Empurre.	Trancado.	Nenhuma
Desbloqueado	moedas	Desbloqueado	Nenhuma
Desbloqueado	Empurre.	Trancado.	Quando o cliente tiver empurrado, bloqueia o catraca.

A máquina de estado da catraca também pode ser representada por um grafo direcionado chamado diagrama de estado (acima). Cada estado é representado por um nó (círculo). As bordas (setas) mostram as transições de um estado para outro. Cada seta é rotulada com a entrada que aciona essa transição. Uma entrada que não causa uma mudança de estado (como uma entrada moeda no Desbloqueado estado) é representado por uma seta circular retornando ao estado original. A seta no nó Bloqueado do ponto preto indica que é o estado inicial.

Conceitos e terminologia

Um estado é uma descrição do estado de um sistema que está esperando para executar uma transição. Uma transição é um conjunto de ações a serem executadas quando uma condição é satisfeita ou quando um evento é recebido. Por exemplo, ao usar um sistema de áudio para ouvir rádio (o sistema está no estado "rádio"), receber um "próximo" estímulo resulta em mover para a próxima estação. Quando o sistema está no "CD" estado, o "próximo" estímulo resulta em mover para a próxima faixa. Estímulos idênticos desencadeiam ações diferentes dependendo do estado atual.

Em algumas representações de máquina de estado finito, também é possível associar ações a um estado:

uma ação de entrada: realizada quando entrar o estado, e
uma ação de saída: realizada quando sair o estado.

Representações

Fig. 1 Exemplo de gráfico de estado UML (um forno de torradeira)

Fig. 2 exemplo de máquina de estado SDL

Fig. 3 Exemplo de uma máquina de estado finito simples

Tabela de estado/evento

Vários tipos de tabela de transição de estado são usados. A representação mais comum é mostrada abaixo: a combinação do estado atual (por exemplo, B) e entrada (por exemplo, Y) mostra o próximo estado (por exemplo, C). As informações da ação completa não são descritas diretamente na tabela e só podem ser adicionadas usando notas de rodapé. Uma definição de FSM incluindo as informações completas da ação é possível usando tabelas de estado (consulte também máquina virtual de estado finito).

Quadro de transição estatal
Corrente Estado Entrada	Estado A	Estado B	Estado C
Entrada X	...	...	...
Entrada Y	...	Estado C	...
Entrada Z	...	...	...

Máquinas de estado UML

A Unified Modeling Language tem uma notação para descrever máquinas de estado. As máquinas de estado UML superam as limitações das máquinas de estado finito tradicionais, mantendo seus principais benefícios. As máquinas de estado UML introduzem os novos conceitos de estados aninhados hierarquicamente e regiões ortogonais, enquanto estendem a noção de ações. As máquinas de estado UML têm as características das máquinas de Mealy e das máquinas de Moore. Eles suportam ações que dependem tanto do estado do sistema quanto do evento desencadeador, como nas máquinas de Mealy, bem como ações de entrada e saída, que estão associadas a estados em vez de transições, como nas máquinas de Moore.

Máquinas de estado SDL

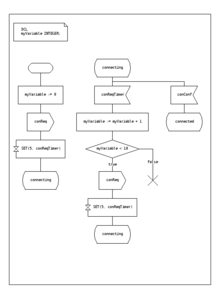
A Linguagem de Especificação e Descrição é um padrão da ITU que inclui símbolos gráficos para descrever ações na transição:

enviar um evento
receber um evento
começar um temporizador
cancelar um temporizador
iniciar outra máquina de estado concorrente
Decisão

SDL incorpora tipos de dados básicos chamados "Tipos de dados abstratos", uma linguagem de ação e uma semântica de execução para tornar a máquina de estado finito executável.

Outros diagramas de estado

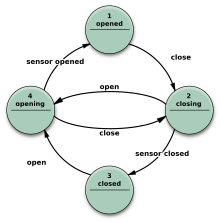
Há um grande número de variantes para representar uma FSM como a da figura 3.

Uso

Além de seu uso na modelagem de sistemas reativos apresentados aqui, as máquinas de estado finito são importantes em muitas áreas diferentes, incluindo engenharia elétrica, linguística, ciência da computação, filosofia, biologia, matemática, programação de videogames e lógica. As máquinas de estado finito são uma classe de autômatos estudados na teoria dos autômatos e na teoria da computação. Na ciência da computação, as máquinas de estado finito são amplamente utilizadas na modelagem do comportamento de aplicativos (teoria de controle), projeto de sistemas digitais de hardware, engenharia de software, compiladores, protocolos de rede e linguística computacional.

Classificação

Máquinas de estado finito podem ser subdivididas em aceitadores, classificadores, transdutores e sequenciadores.

Aceitadores

Fig. 4: Aceitador FSM: analisando a corda "nice".

Fig. 5: Representação de um aceitador; este exemplo mostra um que determina se um número binário tem um número igual de 0s, onde S₁ é um aceitando o estado e S₂ é um estado não aceitando.

Aceitadores (também chamados de detectores ou reconhecedores) produzem uma saída binária, indicando se a entrada recebida é aceita ou não. Cada estado de um aceitador é aceitando ou não aceitando. Depois que todas as entradas forem recebidas, se o estado atual for um estado de aceitação, a entrada será aceita; caso contrário, é rejeitado. Via de regra, a entrada é uma sequência de símbolos (caracteres); ações não são usadas. O estado inicial também pode ser um estado de aceitação, caso em que o aceitador aceita a string vazia. O exemplo na figura 4 mostra um aceitador que aceita a string "nice". Neste aceitador, o único estado de aceitação é o estado 7.

Um conjunto (possivelmente infinito) de sequências de símbolos, chamado de linguagem formal, é uma linguagem regular se houver algum aceitador que aceite exatamente esse conjunto. Por exemplo, o conjunto de strings binárias com um número par de zeros é uma linguagem regular (cf. Fig. 5), enquanto o conjunto de todas as strings cujo comprimento é um número primo não é.

Um aceitador também pode ser descrito como definindo uma linguagem que conteria todas as strings aceitas pelo aceitador, mas nenhuma das rejeitadas; esse idioma é aceito pelo aceitante. Por definição, as linguagens aceitas pelos aceitadores são as linguagens regulares.

O problema de determinar a linguagem aceita por um determinado aceitador é uma instância do problema do caminho algébrico - ele próprio uma generalização do problema do caminho mais curto para grafos com arestas ponderadas pelos elementos de um semi-anel (arbitrário).

Um exemplo de um estado de aceitação aparece na Fig. 5: um autômato finito determinístico (DFA) que detecta se a string de entrada binária contém um número par de 0s.

S₁ (que também é o estado inicial) indica o estado no qual um número par de 0s foi inserido. S₁ é, portanto, um estado de aceitação. Este aceitador terminará em um estado de aceitação, se a string binária contiver um número par de 0s (incluindo qualquer string binária que não contenha 0s). Exemplos de strings aceitas por este aceitador são ε (a string vazia), 1, 11, 11..., 00, 010, 1010, 10110, etc.

Classificadores

Classificadores são uma generalização de aceitadores que produzem uma saída n-ária onde n é estritamente maior que dois.

Transdutores

Fig. 6 Transdutor FSM: Exemplo de modelo de Moore

Fig. 7 Transdutor FSM: Exemplo de modelo simples

Transdutores produzem saída com base em uma determinada entrada e/ou um estado usando ações. Eles são usados para aplicações de controle e no campo da linguística computacional.

Em aplicações de controle, dois tipos são diferenciados:

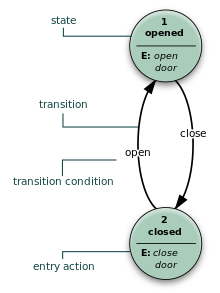
Máquina de Moore: O FSM usa apenas ações de entrada, ou seja, a saída depende apenas do estado. A vantagem do modelo Moore é uma simplificação do comportamento. Considere uma porta do elevador. A máquina do estado reconhece dois comandos: "command_open" e "command_close", que desencadeiam mudanças do estado. A ação de entrada (E:) no estado "Opening" inicia um motor abrindo a porta, a ação de entrada no estado "Closing" inicia um motor na outra direção fechando a porta. Os Estados "Abertos" e "A Fechados" param o motor quando totalmente aberto ou fechado. Eles sinalizam para o mundo exterior (por exemplo, para outras máquinas estatais) a situação: "a porta está aberta" ou "a porta está fechada".

Máquina de limpeza: O FSM também usa ações de entrada, ou seja, a saída depende de entrada e estado. O uso de um FSM Mealy leva muitas vezes a uma redução do número de estados. O exemplo na figura 7 mostra um Mealy FSM implementando o mesmo comportamento que no exemplo de Moore (o comportamento depende do modelo de execução FSM implementado e funcionará, por exemplo, para FSM virtual, mas não para FSM conduzido por eventos). Há duas ações de entrada (I:): "iniciar motor para fechar a porta se command_close chegar" e "iniciar motor na outra direção para abrir a porta se command_open chegar". Os estados intermediários "abertura" e "colamento" não são mostrados.

Sequenciadores

Sequenciadores (também chamados de geradores) são uma subclasse de aceitadores e transdutores que possuem um alfabeto de entrada de uma única letra. Eles produzem apenas uma sequência, que pode ser vista como uma sequência de saída de aceitadores ou saídas de transdutores.

Determinismo

Outra distinção é entre autômatos determinísticos (DFA) e não determinísticos (NFA, GNFA). Em um autômato determinístico, todo estado tem exatamente uma transição para cada entrada possível. Em um autômato não determinístico, uma entrada pode levar a uma, mais de uma ou nenhuma transição para um determinado estado. O algoritmo de construção powerset pode transformar qualquer autômato não determinístico em um (geralmente mais complexo) autômato determinístico com funcionalidade idêntica.

Uma máquina de estado finito com apenas um estado é chamada de "FSM combinatória". Ele só permite ações na transição para um estado. Este conceito é útil nos casos em que várias máquinas de estado finito são necessárias para trabalhar juntas e quando é conveniente considerar uma parte puramente combinatória como uma forma de FSM para atender às ferramentas de projeto.

Semântica alternativa

Existem outros conjuntos de semântica disponíveis para representar máquinas de estado. Por exemplo, existem ferramentas para modelar e projetar lógica para controladores embarcados. Eles combinam máquinas de estado hierárquicas (que geralmente têm mais de um estado atual), gráficos de fluxo e tabelas de verdade em uma linguagem, resultando em um formalismo e um conjunto de semântica diferentes. Esses gráficos, como as máquinas de estado originais de Harel, suportam estados aninhados hierarquicamente, regiões ortogonais, ações de estado e ações de transição.

Modelo matemático

De acordo com a classificação geral, encontram-se as seguintes definições formais.

A máquina de estado finito determinístico ou aceitador de estado finito determinístico é um quintupla $(SigmaS,s_{0},deltaF)$ Onde:

$Sigma$ é o alfabeto de entrada (um conjunto finito não vazio de símbolos);
$S$ é um conjunto finito de estados não vazios;
$s_{0}$ é um estado inicial, um elemento de $S$ ;
$delta$ é a função de transição estatal: $delta:Stimes Sigma rightarrow S$ (em um autômato finito nondeterminístico seria $delta:Stimes Sigma rightarrow {mathcal {P}}(S)$ , i.e. $delta$ retornaria um conjunto de estados);
$F$ é o conjunto de estados finais, um subconjunto (possivelmente vazio) de $S$ .

Para FSMs determinísticos e não determinísticos, é convencional permitir $delta$ para ser uma função parcial, ou seja, ${displaystyle delta (s,x)}$ não tem que ser definido para cada combinação de ${displaystyle sin S}$ e $xin Sigma$ . Se um FSM $M$ está em um estado $s$ , o próximo símbolo é $x$ e ${displaystyle delta (s,x)}$ não é definido, então $M$ pode anunciar um erro (ou seja, rejeitar a entrada). Isso é útil em definições de máquinas estatais gerais, mas menos útil ao transformar a máquina. Alguns algoritmos em seu formulário padrão podem exigir funções totais.

Uma máquina de estado finito tem o mesmo poder computacional que uma máquina de Turing que é restrita de forma que seu cabeçote só pode executar "ler" operações, e sempre tem que se mover da esquerda para a direita. Ou seja, cada linguagem formal aceita por uma máquina de estado finito é aceita por esse tipo de máquina de Turing restrita e vice-versa.

A transdutor de estado finito é um sextuple $(SigmaGammaS,s_{0},deltaomega)$ Onde:

$Sigma$ é o alfabeto de entrada (um conjunto finito não vazio de símbolos);
$Gamma$ é o alfabeto de saída (um conjunto finito não vazio de símbolos);
$S$ é um conjunto finito de estados não vazios;
$s_{0}$ é o estado inicial, um elemento de $S$ ;
$delta$ é a função de transição estatal: $delta:Stimes Sigma rightarrow S$ ;
$omega$ é a função de saída.

Se a função de saída depende do símbolo de estado e entrada ( $omega:Stimes Sigma rightarrow Gamma$ ) essa definição corresponde à Modelo de Mealy, e pode ser modelado como uma máquina Mealy. Se a função de saída depende apenas do estado ( $omega:Srightarrow Gamma$ ) essa definição corresponde à Modelo de Moore, e pode ser modelado como uma máquina Moore. Uma máquina de estado finito sem função de saída é conhecida como um sistema de semiautomaton ou transição.

Se desconsiderarmos o primeiro símbolo de saída de uma máquina Moore, ${displaystyle omega (s_{0})}$ , então pode ser facilmente convertido para uma saída equivalente Mealy máquina, definindo a função de saída de cada transição Mealy (ou seja, rotulando cada borda) com o símbolo de saída dado do estado de destino Moore. A transformação conversa é menos direta porque um estado da máquina Mealy pode ter diferentes rótulos de saída em suas transições de entrada (bordas). Cada estado precisa ser dividido em vários estados de máquina Moore, um para cada símbolo de saída de incidente.

Otimização

Otimizar um FSM significa encontrar uma máquina com o número mínimo de estados que execute a mesma função. O algoritmo conhecido mais rápido que faz isso é o algoritmo de minimização de Hopcroft. Outras técnicas incluem o uso de uma tabela de implicação ou o procedimento de redução de Moore. Além disso, FSAs acíclicos podem ser minimizados em tempo linear.

Implementação

Aplicativos de hardware

Fig. 9 O diagrama de circuito para um contador TTL de 4 bits, um tipo de máquina de estado

Em um circuito digital, um FSM pode ser construído usando um dispositivo lógico programável, um controlador lógico programável, portas lógicas e flip-flops ou relés. Mais especificamente, uma implementação de hardware requer um registrador para armazenar variáveis de estado, um bloco de lógica combinacional que determina a transição de estado e um segundo bloco de lógica combinacional que determina a saída de um FSM. Uma das implementações clássicas de hardware é o controlador Richards.

Em uma máquina de Medvedev, a saída é conectada diretamente aos flip-flops de estado, minimizando o atraso de tempo entre os flip-flops e a saída.

Por meio da codificação de estado para máquinas de estado de baixo consumo de energia, as máquinas podem ser otimizadas para minimizar o consumo de energia.

Aplicativos de software

Os seguintes conceitos são comumente usados para construir aplicativos de software com máquinas de estado finito:

Programação baseada em Automata
Máquina de estado finito dirigida a eventos
Máquina de estado finito virtual
Padrão de design de Estado

Máquinas de estado finito e compiladores

Autômatos finitos são freqüentemente usados no frontend de compiladores de linguagens de programação. Tal frontend pode incluir várias máquinas de estado finito que implementam um analisador léxico e um parser. A partir de uma sequência de caracteres, o analisador léxico constrói uma sequência de tokens de linguagem (como palavras reservadas, literais e identificadores) a partir da qual o analisador constrói uma árvore sintática. O analisador léxico e o analisador lidam com as partes regulares e livres de contexto da gramática da linguagem de programação.

Contenido relacionado

Más resultados...