Magnitude absoluta

Magnitude absoluta (M) é uma medida da luminosidade de um objeto celeste em uma escala de magnitude astronômica logarítmica inversa. A magnitude absoluta de um objeto é definida como sendo igual à magnitude aparente que o objeto teria se fosse visto de uma distância de exatamente 10 parsecs (32,6 anos-luz), sem extinção (ou escurecimento) de sua luz devido à absorção pela matéria interestelar e poeira cósmica. Ao colocar hipoteticamente todos os objetos a uma distância de referência padrão do observador, suas luminosidades podem ser comparadas diretamente entre si em uma escala de magnitude.

Tal como acontece com todas as magnitudes astronômicas, a magnitude absoluta pode ser especificada para diferentes faixas de comprimento de onda correspondentes a bandas de filtro ou bandas passantes especificadas; para estrelas, uma magnitude absoluta comumente citada é a magnitude visual absoluta, que usa a banda visual (V) do espectro (no sistema fotométrico UBV). As magnitudes absolutas são indicadas por um M maiúsculo, com um subscrito representando a faixa de filtro usada para medição, como M_V para magnitude absoluta na banda V.

Quanto mais luminoso um objeto, menor o valor numérico de sua magnitude absoluta. Uma diferença de 5 magnitudes entre as magnitudes absolutas de dois objetos corresponde a uma razão de 100 em suas luminosidades, e uma diferença de n magnitudes em magnitude absoluta corresponde a uma razão de luminosidade de 100^n/5. Por exemplo, uma estrela de magnitude absoluta M_V = 3,0 seria 100 vezes mais luminosa que uma estrela de magnitude absoluta M_V = 8,0 medida na banda do filtro V. O Sol tem magnitude absoluta M_V = +4,83. Objetos altamente luminosos podem ter magnitudes absolutas negativas: por exemplo, a Via Láctea tem uma magnitude B absoluta de cerca de -20,8.

A magnitude bolométrica absoluta de um objeto (M_bol) representa sua luminosidade total em todos os comprimentos de onda, em vez de em uma única faixa de filtro, conforme expresso em um escala de magnitude logarítmica. Para converter de uma magnitude absoluta em uma banda de filtro específica para magnitude bolométrica absoluta, uma correção bolométrica (BC) é aplicada.

Para corpos do Sistema Solar que brilham na luz refletida, uma definição diferente de magnitude absoluta (H) é usada, com base em uma distância de referência padrão de uma unidade astronômica.

Estrelas e galáxias

Na astronomia estelar e galáctica, a distância padrão é de 10 parsecs (cerca de 32,616 anos-luz, 308,57 petametros ou 308,57 trilhões de quilômetros). Uma estrela a 10 parsecs tem uma paralaxe de 0,1″ (100 miliarcosegundos). Galáxias (e outros objetos extensos) são muito maiores do que 10 parsecs, sua luz é irradiada sobre um trecho estendido do céu e seu brilho geral não pode ser observado diretamente de distâncias relativamente curtas, mas a mesma convenção é usada. A magnitude de uma galáxia é definida medindo toda a luz irradiada sobre todo o objeto, tratando esse brilho integrado como o brilho de uma única fonte pontual ou estelar e calculando a magnitude dessa fonte pontual como pareceria se observado na distância padrão de 10 parsecs. Consequentemente, a magnitude absoluta de qualquer objeto é igual à magnitude aparente que teria se estivesse a 10 parsecs de distância.

Algumas estrelas visíveis a olho nu têm uma magnitude absoluta tão baixa que pareceriam brilhantes o suficiente para ofuscar os planetas e projetar sombras se estivessem a 10 parsecs da Terra. Os exemplos incluem Rigel (-7,0), Deneb (-7,2), Naos (-6,0) e Betelgeuse (-5,6). Para comparação, Sirius tem uma magnitude absoluta de apenas 1,4, que ainda é mais brilhante que o Sol, cuja magnitude visual absoluta é de 4,83. A magnitude bolométrica absoluta do Sol é definida arbitrariamente, geralmente em 4,75. As magnitudes absolutas das estrelas geralmente variam de aproximadamente -10 a +20. As magnitudes absolutas das galáxias podem ser muito menores (mais brilhantes). Por exemplo, a galáxia elíptica gigante M87 tem uma magnitude absoluta de -22 (ou seja, tão brilhante quanto cerca de 60.000 estrelas de magnitude -10). Alguns núcleos galácticos ativos (quasares como CTA-102) podem atingir magnitudes absolutas superiores a -32, tornando-os os objetos persistentes mais luminosos no universo observável, embora esses objetos possam variar em brilho em escalas de tempo astronomicamente curtas. No extremo, o brilho óptico da explosão de raios gama GRB 080319B atingiu, de acordo com um artigo, uma magnitude r absoluta mais brilhante que -38 por algumas dezenas de segundos.

Magnitude aparente

O astrônomo grego Hiparco estabeleceu uma escala numérica para descrever o brilho de cada estrela que aparece no céu. As estrelas mais brilhantes no céu receberam uma magnitude aparente m = 1, e as estrelas mais fracas visíveis a olho nu foram atribuídas m = 6. A diferença entre eles corresponde a um fator de 100 no brilho. Para objetos na vizinhança imediata do Sol, a magnitude absoluta M e a magnitude aparente m de qualquer distância d (em parsecs, com 1 pc = 3,2616 anos-luz) estão relacionados por

100.m- Sim. - Sim. M5= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =F10.F= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(D10.pc)2,{displaystyle 100^{frac Não. {F_{10}}{F}}=left({frac {d}{10;mathrm {pc} }}right)^{2},}

M= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =m- Sim. - Sim. 5log10.⁡ ⁡ (DPC)+5= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =m- Sim. - Sim. 5(log10.⁡ ⁡ DPC- Sim. - Sim. 1),{displaystyle M=m-5log _{10}(d_{text{pc}}+5=m-5left(log _{10}d_{text{pc}}-1right),}

Para objetos a distâncias muito grandes (fora da Via Láctea), a distância de luminosidade d_L (distância definida usando medições de luminosidade) deve ser usado em vez de d, porque a aproximação euclidiana é inválida para objetos distantes. Em vez disso, a relatividade geral deve ser levada em conta. Além disso, o redshift cosmológico complica a relação entre magnitude absoluta e aparente, porque a radiação observada foi deslocada para a faixa vermelha do espectro. Para comparar as magnitudes de objetos muito distantes com as de objetos locais, pode ser necessário aplicar uma correção K às magnitudes dos objetos distantes.

A magnitude absoluta M também pode ser escrita em termos de magnitude aparente m e paralaxe estelar p:

M= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =m+5(log10.⁡ ⁡ p+1),{displaystyle M=m+5left(log _{10}p+1right),}

M= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =m- Sim. - Sim. μ μ .Não. M=m-mu.}

Exemplos

Rigel tem uma magnitude visual m_V de 0,12 e distância de cerca de 860 anos-luz:

MV= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0,12- Sim. - Sim. 5(log10.⁡ ⁡ 8603.2616- Sim. - Sim. 1)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. 7.0.{displaystyle M_{mathrm {V} }=0.12-5left(log _{10}{frac {860}{3.2616}}-1right)=-7.0.}

Vega tem uma paralaxe p de 0,129″ e uma magnitude aparente m_V de 0,03:

MV= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0,03+5(log10.⁡ ⁡ 0,129+1)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =+0.6.{displaystyle M_{mathrm {V} }=0.03+5left(log _{10}{0.129}+1right)=+0.6.}

A Galáxia Black Eye tem uma magnitude visual m_V de 9,36 e um módulo de distância μ de 31.06:

MV= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =9.36- Sim. - Sim. 31.06= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. 21.7.- Sim. 9.36-31.06=-21.7.}

Magnitude bolométrica

A magnitude absoluta bolométrica M_bol, leva em consideração a radiação eletromagnética em todos os comprimentos de onda. Inclui aqueles não observados devido à banda passante instrumental, à absorção atmosférica da Terra e à extinção pela poeira interestelar. É definido com base na luminosidade das estrelas. No caso de estrelas com poucas observações, deve ser calculado assumindo uma temperatura efetiva.

Classicamente, a diferença na magnitude bolométrica está relacionada com a razão de luminosidade de acordo com:

Mb)oEu...,Detalhe Detalhe - Sim. - Sim. Mb)oEu...,⊙ ⊙ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. 2.5.log10.⁡ ⁡ (LDetalhe Detalhe L⊙ ⊙ )Não. M_{mathrm {bol,star } }-M_{mathrm {bol,odot } }=-2.5log _{10}left({frac {L_{star }}{L_{odot }}}right)}

LDetalhe Detalhe L⊙ ⊙ = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =10.0(Mb)oEu...,⊙ ⊙ - Sim. - Sim. Mb)oEu...,Detalhe Detalhe )(L_{star) }}}=10^{0.4left(M_{mathrm {bol,odot } }-M_{mathrm {bol,star } }right)}}

• L_⊙ é a luminosidade do Sol (luminosidade lipométrica)
• L_★ é a luminosidade da estrela (luminosidade lipométrica)
• M_Bol, é a magnitude bolométrica do Sol
• M_bol,★ é a magnitude bolométrica da estrela.

Em agosto de 2015, a União Astronômica Internacional aprovou a Resolução B2 definindo os pontos zero das escalas de magnitude bolométrica absoluta e aparente em unidades SI para potência (watts) e irradiância (W/m²), respectivamente. Embora as magnitudes bolométricas tenham sido usadas pelos astrônomos por muitas décadas, houve diferenças sistemáticas nas escalas de magnitude absoluta-luminosidade apresentadas em várias referências astronômicas e nenhuma padronização internacional. Isso levou a diferenças sistemáticas nas escalas de correções bolométricas. Combinado com magnitudes bolométricas absolutas incorretas assumidas para o Sol, isso pode levar a erros sistemáticos nas luminosidades estelares estimadas (e outras propriedades estelares, como raios ou idades, que dependem da luminosidade estelar para serem calculadas).

A resolução B2 define uma escala de magnitude bolométrica absoluta onde M_bol = 0 corresponde à luminosidade L₀ = 3.0128×10²⁸ W, com a luminosidade do ponto zero L₀ definido de forma que o Sol (com luminosidade nominal 3.828×10²⁶ W) corresponde à magnitude bolométrica absoluta M_bol,⊙ = 4,74. Colocando uma fonte de radiação (por exemplo, estrela) na distância padrão de 10 parsecs, segue-se que o ponto zero da escala de magnitude bolométrica aparente m_bol = 0 corresponde à irradiância f₀ = 2.518021002 ×10⁻⁸ L/m². Usando a escala IAU 2015, a irradiância solar total nominal ("constante solar") medida em 1 unidade astronômica (1361 W/m²) corresponde a uma magnitude bolométrica aparente do Sol de m_bol,⊙ = −26.832.

Seguindo a Resolução B2, a relação entre a magnitude bolométrica absoluta de uma estrela e sua luminosidade não está mais diretamente ligada à luminosidade (variável) do Sol:

Mb)oEu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. 2.5.log10.⁡ ⁡ LDetalhe Detalhe L0? ? - Sim. - Sim. 2.5.log10.⁡ ⁡ LDetalhe Detalhe +71.197425Não. M_{mathrm {bol} }=-2.5log _{10}{frac Não. }}{L_{0}}}approx -2.5log _{10}L_{star }+71.197425}

• L_★ é a luminosidade da estrela (luminosidade lipométrica) em watts
• L₀ é o ponto zero luminosidade 3.0128×10.²⁸W
• M_Bolo é a magnitude bolométrica da estrela

A nova escala de magnitude absoluta da IAU desconecta permanentemente a escala da variável Sol. No entanto, nesta escala de potência do SI, a luminosidade solar nominal corresponde aproximadamente a M_bol = 4,74, um valor que foi comumente adotado por astrônomos antes da resolução de 2015 da IAU.

A luminosidade da estrela em watts pode ser calculada em função de sua magnitude bolométrica absoluta M_bol como:

LDetalhe Detalhe = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =L010.- Sim. - Sim. 0Mb)oEu...- Sim. }=L_{0}10^{-0.4M_{mathrm {bol} }}}

Corpos do Sistema Solar (H)

Para planetas e asteróides, uma definição de magnitude absoluta que é mais significativa para objetos não estelares é usada. A magnitude absoluta, comumente chamada H. H. H.Não. H., é definido como a magnitude aparente que o objeto teria se fosse uma unidade astronômica (AU) tanto do Sol quanto do observador, e em condições de oposição solar ideal (um arranjo que é impossível na prática). Como os corpos do Sistema Solar são iluminados pelo Sol, seu brilho varia como uma função de condições de iluminação, descrita pelo ângulo de fase. Esta relação é chamada de curva de fase. A magnitude absoluta é o brilho no ângulo de fase zero, um arranjo conhecido como oposição, de uma distância de uma UA.

Magnitude aparente

O ângulo de fase α α - Sim. pode ser calculado a partir das distâncias corpo-sol, observador-sol e corpo-observador, usando a lei de cosines.

A magnitude absoluta H. H. H.Não. H. pode ser usado para calcular a magnitude aparente mNão. de um corpo. Para um objeto que reflete a luz solar, H. H. H.Não. H. e mNão. são conectados pela relação

m= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =H. H. H.+5log10.⁡ ⁡ (DBSDBOD02)- Sim. - Sim. 2.5.log10.⁡ ⁡ q(α α ),{displaystyle m=H+5log _{10}{left({frac) {d_{BS}d_{BO}}{d_{0}^{2}}}right)}-2.5log _{10}{q(alpha)},}

α α - Sim.

q(α α ){displaystyle q(alpha)}

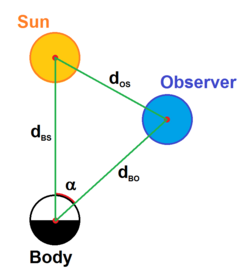
Pela lei dos cossenos, temos:

e⁡ ⁡ α α = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =DBO2+DBS2- Sim. - Sim. DOS22DBODBS.{displaystyle cos} ? Não. - Não. {BS} }^{2}-d_{mathrm {OS} }^{2}}{2d_{mathrm {BO} }d_{mathrm Sim.

Distâncias:

• D_BOA é a distância entre o corpo e o observador
• D_BS é a distância entre o corpo e o Sol
• D_OS é a distância entre o observador e o Sol
• D₀, um fator de conversão de unidade, é a constante 1 UA, a distância média entre a Terra e o Sol

Aproximações para a integral de fase q(α)

O valor de q(α α ){displaystyle q(alpha)} depende das propriedades da superfície reflectora, em particular da sua rugosidade. Na prática, diferentes aproximações são usadas com base nas propriedades conhecidas ou assumidas da superfície. As superfícies dos planetas terrestres são geralmente mais difíceis de modelar do que as dos planetas gasosos, as últimas têm superfícies visíveis mais suaves.

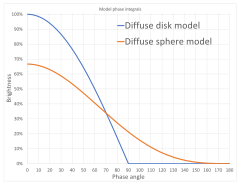
Planetas como esferas difusas

Reflexão de difuso na esfera e no disco plano

Brilho com fase para modelos de reflexão difusa. A esfera é 2/3 tão brilhante em zero fase, enquanto o disco não pode ser visto além de 90 graus.

Corpos planetários podem ser aproximados razoavelmente bem como esferas de reflexão difusa ideais. Vamos. α α - Sim. ser o ângulo de fase em graus, então

q(α α )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =23((1- Sim. - Sim. α α 180∘ ∘ )e⁡ ⁡ α α +1D D pecado⁡ ⁡ α α ).{displaystyle q(alpha)={frac {2}{3}}left(left(1-{frac {alpha }{180^{circ }}}right)cos {alpha }+{frac {1}{pi }}sin {alpha }right). ?

α α = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =90∘ ∘ {displaystyle alpha =90^{circ }}

1D D - Sim. Não.)

α α = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0∘ ∘ {displaystyle alpha =0^{circ)

Pelo contrário, modelo difuso do refletor do disco é simplesmente q(α α )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =e⁡ ⁡ α α {displaystyle q(alpha)=cos {alpha }}, que não é realista, mas representa a onda de oposição para superfícies ásperas que refletem a luz mais uniforme de volta em ângulos de baixa fase.

A definição do albedo geométrico pNão., uma medida para a refletividade de superfícies planetárias, é baseada no modelo de refletor de disco difuso. A magnitude absoluta H. H. H.Não. H., diâmetro DNão. (em quilômetros) e albedo geométrico pNão. de um corpo estão relacionados por

D= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1329p× × 10.- Sim. - Sim. 0,2H. H. H.km.{displaystyle D={frac {1329}{sqrt {p}}}times 10^{-0.2H}mathrm {km}.}

Exemplo: A magnitude absoluta da Lua H. H. H.Não. H. pode ser calculado a partir do seu diâmetro D= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =3474km{displaystyle D=3474{text{ km}}} e albedo geométrico p= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0,113Não.:

H. H. H.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =5log10.⁡ ⁡ 132934740,113= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =+0,28.{displaystyle H=5log _{10}{frac {1329}{3474{sqrt {0.113}}=+0.28.}

DBS= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1AUNão. d_{BS}=1{text{ AU}}}

DBO= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =384400km= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0,00257AU.Não. d_{BO}=384400{text{ km}}=0.00257{text{ AU}}}

q(α α )? ? 23D D {textstyle q(alpha)approx {frac {2}{3pi }}}

m= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =+0,28+5log10.⁡ ⁡ (1)) 0,00257)- Sim. - Sim. 2.5.log10.⁡ ⁡ (23D D )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. 10,99.{textstyle m=+0.28+5log _{10}{left(1cdot 0.00257right)}-2.5log _{10}{left({frac {2}{3pi }}right)}=-10.99.}

m= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. 10.0.- Sim.

Modelos mais avançados

Como os corpos do Sistema Solar nunca são reflexos difusos perfeitos, os astrônomos usam modelos diferentes para prever magnitudes aparentes baseadas em propriedades conhecidas ou assumidas do corpo. Para planetas, aproximações para o termo de correção - Sim. - Sim. 2.5.log10.⁡ ⁡ q(α α ){displaystyle -2.5log _{10}{q(alpha)}} na fórmula para m foram derivados empiricamente, para combinar observações em diferentes ângulos de fase. As aproximações recomendadas pelo Almanac astronômico são (com α α - Sim. em graus):

Planet	H {displaystyle H}	Approximation for − 2.5 log 10 ⁡ q ( α ) {displaystyle -2.5log _{10}{q(alpha)}}
Mercury	−0.613	+ 6.328 × 10 − 2 α − 1.6336 × 10 − 3 α 2 + 3.3644 × 10 − 5 α 3 − 3.4265 × 10 − 7 α 4 + 1.6893 × 10 − 9 α 5 − 3.0334 × 10 − 12 α 6 {displaystyle +6.328times 10^{-2}alpha -1.6336times 10^{-3}alpha ^{2}+3.3644times 10^{-5}alpha ^{3}-3.4265times 10^{-7}alpha ^{4}+1.6893times 10^{-9}alpha ^{5}-3.0334times 10^{-12}alpha ^{6}}
Venus	−4.384	− 1.044 × 10 − 3 α + 3.687 × 10 − 4 α 2 − 2.814 × 10 − 6 α 3 + 8.938 × 10 − 9 α 4 {displaystyle -1.044times 10^{-3}alpha +3.687times 10^{-4}alpha ^{2}-2.814times 10^{-6}alpha ^{3}+8.938times 10^{-9}alpha ^{4}} (for 0 ∘ < α ≤ 163.7 ∘ {displaystyle 0^{circ }<alpha leq 163.7^{circ }} ) + 240.44228 − 2.81914 α + 8.39034 × 10 − 3 α 2 {displaystyle +240.44228-2.81914alpha +8.39034times 10^{-3}alpha ^{2}} (for 163.7 ∘ < α < 179 ∘ {displaystyle 163.7^{circ }<alpha <179^{circ }} )
Earth	−3.99	− 1.060 × 10 − 3 α + 2.054 × 10 − 4 α 2 {displaystyle -1.060times 10^{-3}alpha +2.054times 10^{-4}alpha ^{2}}
Moon	+0.28	+ 2.9994 × 10 − 2 α − 1.6057 × 10 − 4 α 2 + 3.1543 × 10 − 6 α 3 − 2.0667 × 10 − 8 α 4 + 6.2553 × 10 − 11 α 5 {displaystyle +2.9994times 10^{-2}alpha -1.6057times 10^{-4}alpha ^{2}+3.1543times 10^{-6}alpha ^{3}-2.0667times 10^{-8}alpha ^{4}+6.2553times 10^{-11}alpha ^{5}} (for α ≤ 150 ∘ {displaystyle alpha leq 150^{circ }} , before full Moon) + 3.3234 × 10 − 2 α − 3.0725 × 10 − 4 α 2 + 6.1575 × 10 − 6 α 3 − 4.7723 × 10 − 8 α 4 + 1.4681 × 10 − 10 α 5 {displaystyle +3.3234times 10^{-2}alpha -3.0725times 10^{-4}alpha ^{2}+6.1575times 10^{-6}alpha ^{3}-4.7723times 10^{-8}alpha ^{4}+1.4681times 10^{-10}alpha ^{5}} (for α ≤ 150 ∘ {displaystyle alpha leq 150^{circ }} , after full Moon)
Mars	−1.601	+ 2.267 × 10 − 2 α − 1.302 × 10 − 4 α 2 {displaystyle +2.267times 10^{-2}alpha -1.302times 10^{-4}alpha ^{2}} (for 0 ∘ < α ≤ 50 ∘ {displaystyle 0^{circ }<alpha leq 50^{circ }} ) + 1.234 − 2.573 × 10 − 2 α + 3.445 × 10 − 4 α 2 {displaystyle +1.234-2.573times 10^{-2}alpha +3.445times 10^{-4}alpha ^{2}} (for 50 ∘ < α ≤ 120 ∘ {displaystyle 50^{circ }<alpha leq 120^{circ }} )
Jupiter	−9.395	− 3.7 × 10 − 4 α + 6.16 × 10 − 4 α 2 {displaystyle -3.7times 10^{-4}alpha +6.16times 10^{-4}alpha ^{2}} (for α ≤ 12 ∘ {displaystyle alpha leq 12^{circ }} ) − 0.033 − 2.5 log 10 ⁡ ( 1 − 1.507 ( α 180 ∘ ) − 0.363 ( α 180 ∘ ) 2 − 0.062 ( α 180 ∘ ) 3 + 2.809 ( α 180 ∘ ) 4 − 1.876 ( α 180 ∘ ) 5 ) {displaystyle -0.033-2.5log _{10}{left(1-1.507left({frac {alpha }{180^{circ }}}right)-0.363left({frac {alpha }{180^{circ }}}right)^{2}-0.062left({frac {alpha }{180^{circ }}}right)^{3}+2.809left({frac {alpha }{180^{circ }}}right)^{4}-1.876left({frac {alpha }{180^{circ }}}right)^{5}right)}} (for α > 12 ∘ {displaystyle alpha >12^{circ }} )
Saturn	−8.914	− 1.825 sin ⁡ ( β ) + 2.6 × 10 − 2 α − 0.378 sin ⁡ ( β ) e − 2.25 α {displaystyle -1.825sin {left(beta right)}+2.6times 10^{-2}alpha -0.378sin {left(beta right)}e^{-2.25alpha }} (for planet and rings, α < 6.5 ∘ {displaystyle alpha <6.5^{circ }} and β < 27 ∘ {displaystyle beta <27^{circ }} ) − 0.036 − 3.7 × 10 − 4 α + 6.16 × 10 − 4 α 2 {displaystyle -0.036-3.7times 10^{-4}alpha +6.16times 10^{-4}alpha ^{2}} (for the globe alone, α ≤ 6 ∘ {displaystyle alpha leq 6^{circ }} ) + 0.026 + 2.446 × 10 − 4 α + 2.672 × 10 − 4 α 2 − 1.505 × 10 − 6 α 3 + 4.767 × 10 − 9 α 4 {displaystyle +0.026+2.446times 10^{-4}alpha +2.672times 10^{-4}alpha ^{2}-1.505times 10^{-6}alpha ^{3}+4.767times 10^{-9}alpha ^{4}} (for the globe alone, 6 ∘ < α < 150 ∘ {displaystyle 6^{circ }<alpha <150^{circ }} )
Uranus	−7.110	− 8.4 × 10 − 4 ϕ ′ + 6.587 × 10 − 3 α + 1.045 × 10 − 4 α 2 {displaystyle -8.4times 10^{-4}phi '+6.587times 10^{-3}alpha +1.045times 10^{-4}alpha ^{2}} (for α < 3.1 ∘ {displaystyle alpha <3.1^{circ }} )
Neptune	−7.00	+ 7.944 × 10 − 3 α + 9.617 × 10 − 5 α 2 {displaystyle +7.944times 10^{-3}alpha +9.617times 10^{-5}alpha ^{2}} (for α < 133 ∘ {displaystyle alpha <133^{circ }} and t > 2000.0 {displaystyle t>2000.0} )

As diferentes metades da Lua, como visto da Terra

Lua no primeiro trimestre

Lua no último trimestre

Aqui. β β - Sim. é a inclinação eficaz dos anéis de Saturno (sua inclinação em relação ao observador), que, como visto da Terra varia entre 0° e 27° ao longo de uma órbita de Saturno, e φ φ ?- Sim. é um pequeno termo de correção dependendo das latitudes sub-Earth e sub-solar de Urano. )Não. é o ano da Era Comum. A magnitude absoluta de Neptuno está mudando lentamente devido aos efeitos sazonais à medida que o planeta se move ao longo de sua órbita de 165 anos ao redor do Sol, e a aproximação acima só é válida após o ano 2000. Para algumas circunstâncias, como α α ≥ ≥ 179∘ ∘ {displaystyle alpha geq 179^{circ }} para Vênus, não há observações disponíveis, e a curva de fase é desconhecida nesses casos. A fórmula para a Lua só é aplicável ao lado próximo da Lua, a porção que é visível da Terra.

Exemplo 1: Em 1 de janeiro de 2019, Vénus foi DBS= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0,7519AUNão. d_{BS}=0.719{text{ AU}}} do Sol, e DBO= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0.645AUNão. d_{BO}=0.645{text{ AU}}} da Terra, em um ângulo de fase α α = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =93.0∘ ∘ {displaystyle alpha =93.0^{circ }} (perto da fase trimestre). Sob condições de fase completa, Vénus teria sido visível em m= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. 4.384+5log10.⁡ ⁡ (0,7519)) 0.645)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. 6.09.Não. m=-4.384+5log _{10}{left(0.719cdot 0.645right)}=-6.09.} Contabilidade para o ângulo de alta fase, o termo de correção acima produz uma magnitude aparente real de m= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. 6.09+(- Sim. - Sim. 1.044× × 10.- Sim. - Sim. 3)) 93.0+3.687× × 10.- Sim. - Sim. 4)) 93.02- Sim. - Sim. 2.814× × 10.- Sim. - Sim. 6)) 93.03+8.938× × 10.- Sim. - Sim. 9)) 93.04)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. 4.59.Não. m=-6.09+left(-1.044times 10^{-3}cdot 93.0+3.687times 10^{-4}cdot 93.0^{2}-2.814times 10^{-6}cdot 93.0^{3}+8.938times 10^{-9}cdot 93.0^{4}right)=-4.59.} Isso é perto do valor de m= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. 4.62Não. M=-4.62 previsto pelo Laboratório de Propulsão de Jato.

Exemplo 2: Na primeira fase trimestre, a aproximação para a Lua dá - Sim. - Sim. 2.5.log10.⁡ ⁡ q(90∘ ∘ )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2.71.{textstyle -2.5log _{10}{q(90^{circ })}=2.71.} Com isso, a magnitude aparente da Lua é m= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =+0,28+5log10.⁡ ⁡ (1)) 0,00257)+2.71= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. 9.96,[textstyle m=+0.28+5log _{10}{left(1cdot 0.00257right)}+2.71=-9.96,} perto do valor esperado de cerca de - Sim. - Sim. 10.- Sim.. No último trimestre, a Lua é cerca de 0,06 mag mais fraco do que no primeiro trimestre, porque essa parte de sua superfície tem um albedo inferior.

O albedo da Terra varia por um fator de 6, de 0,12 no caso sem nuvens a 0,76 no caso da nuvem altostratus. A magnitude absoluta na tabela corresponde a um albedo de 0,434. Devido à variabilidade do clima, a magnitude aparente da Terra não pode ser prevista com tanta precisão quanto a da maioria dos outros planetas.

Asteroides

Asteróide 1 Ceres, fotografado pela sonda Dawn em ângulos de fase de 0°, 7° e 33°. A forte diferença de brilho entre os três é real. A imagem esquerda no ângulo de fase de 0° mostra o aumento do brilho devido ao efeito da oposição.

Integrais de fase para vários valores de G

Relação entre o parâmetro inclinação GNão. G. e o aumento da oposição. Maiores valores de GNão. G. corresponde a um efeito de oposição menos pronunciado. Para a maioria dos asteróides, um valor de G= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0,15- Sim. é assumido, correspondendo a uma onda de oposição de 0mago{displaystyle 0,3{text{ mag}}}.

Se um objeto tem uma atmosfera, ele reflete a luz mais ou menos isotrópica em todas as direções, e seu brilho pode ser modelado como um refletor difuso. Corpos sem atmosfera, como asteroides ou luas, tendem a refletir a luz mais fortemente para a direção da luz incidente, e seu brilho aumenta rapidamente à medida que o ângulo de fase se aproxima 0∘ ∘ {displaystyle 0^{circ }}. Este brilho rápido perto da oposição é chamado de efeito da oposição. Sua força depende das propriedades físicas da superfície do corpo, e, portanto, difere do asteróide ao asteróide.

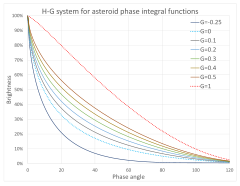
Em 1985, a UAI adotou o semi-empírico H. H. H.GNão. HG-sistema, baseado em dois parâmetros H. H. H.Não. H. e GNão. G. chamado magnitude absoluta e inclinação, para modelar o efeito da oposição para os efêmeros publicados pelo Minor Planet Center.

m= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =H. H. H.+5log10.⁡ ⁡ (DBSDBOD02)- Sim. - Sim. 2.5.log10.⁡ ⁡ q(α α ),{displaystyle m=H+5log _{10}{left({frac) {d_{BS}d_{BO}}{d_{0}^{2}}}right)}-2.5log _{10}{q(alpha)},}

onde

• a integral da fase é q(α α )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(1- Sim. - Sim. G)φ φ 1(α α )+Gφ φ 2(α α ){displaystyle q(alpha)=left(1-Gright)phi _{1}left(alpha right)+Gphi _{2}left(alpha right)} e
• φ φ Eu...(α α )= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =exp⁡ ⁡ (- Sim. - Sim. AEu...(bronzeado⁡ ⁡ α α 2)BEu...){textstyle phi _{i}left(alpha right)=exp {left(-A_{i}left(tan {frac {alpha }{2}}right)^{B_{i}}right)}} para Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1- Sim. ou 2Não. 2, A1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =3.332Não. A_{1}=3.332}, A2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1.862Não. A_{2}=1.862}, B1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0,631Não. B_{1}=0.631} e B2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1.218Não. B_{2}=1.218.

Esta relação é válida para ângulos de fase <math alttext="{displaystyle alpha α α <120∘ ∘ {displaystyle alpha <120^{circ }}<img alt="{displaystyle alpha e funciona melhor quando <math alttext="{displaystyle alpha α α <20.∘ ∘ {displaystyle alpha <20^{circ }}<img alt="{displaystyle alpha .

O parâmetro de inclinação GNão. G. relaciona-se com o aumento do brilho, tipicamente 0, quando o objeto está perto da oposição. É conhecido com precisão apenas por um pequeno número de asteróides, portanto para a maioria dos asteróides um valor de G= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0,15- Sim. é assumido. Em casos raros, GNão. G. pode ser negativo. Um exemplo é 101955 Bennu, com G= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. 0,08- Sim..

Em 2012, H. H. H.GNão. HG-sistema foi oficialmente substituído por um sistema melhorado com três parâmetros H. H. H.Não. H., G1Não. G_{1}} e G2Não. G_{2}}, que produz resultados mais satisfatórios se o efeito da oposição é muito pequeno ou restrito a ângulos de fase muito pequenos. No entanto, a partir de 2022, isto H. H. H.G1G2Não. HG_{1}G_{2}}- o sistema não foi adotado pelo Centro do Planeta Menor nem pelo Laboratório de Propulsão de Jato.

A magnitude aparente dos asteróides varia à medida que giram, em escalas de tempo de segundos a semanas dependendo do período de rotação, até 2mago{displaystyle 2{text{ mag}}} ou mais. Além disso, sua magnitude absoluta pode variar com a direção de visualização, dependendo de sua inclinação axial. Em muitos casos, nem o período de rotação nem a inclinação axial são conhecidos, limitando a previsibilidade. Os modelos apresentados aqui não captam esses efeitos.

Magnitudes cometárias

O brilho dos cometas é dado separadamente como magnitude total (m1Não. m_{1}}, o brilho integrado sobre toda a extensão visível do coma) e magnitude nuclear (m2Não. m_{2}}, o brilho da região central sozinho). Ambos são escalas diferentes da escala de magnitude utilizada para planetas e asteróides, e não pode ser usado para uma comparação de tamanho com a magnitude absoluta de um asteróide H. H. H..

A atividade dos cometas varia com sua distância do Sol. Seu brilho pode ser aproximado como

m1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =M1+2.5.)) KK1log10.⁡ ⁡ (DBSD0)+5log10.⁡ ⁡ (DBOD0)Não. m_{1}=M_{1}+2.5cdot K_{1}log _{10}{left({frac {d_{BS}}{d_{0}}}right)}+5log _{10}{left({frac {d_{BO}}{d_{0}}}right)}}

m2= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =M2+2.5.)) KK2log10.⁡ ⁡ (DBSD0)+5log10.⁡ ⁡ (DBOD0),Não. m_{2}=M_{2}+2.5cdot K_{2}log _{10}{left({frac {d_{BS}}{d_{0}}}right)}+5log _{10}{left({frac {d_{BO}}{d_{0}}}right)},}

m1,2Não. m_{1,2}}

M1,2{displaystyle M_{1,2}}

DBSNão. D_{BS}}

DBONão. D_{BO}}

D0Não. D_{0}}

KK1,2Não. K_{1,2}}

KK= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2Não.

Por exemplo, o fardo do cometa C/2011 L4 (PANSTARRS) pode ser aproximado por M1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =5.41,KK1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =3.69.Não. M_{1}=5.41{text{, }}K_{1}=3.69.} No dia de sua passagem de periélio, 10 de março de 2013, o cometa PANSTARRS foi 0.302AU{displaystyle 0.302{text{ AU}}} do Sol e 1.109AU{displaystyle 1.109{text{ AU}}} da Terra. A magnitude aparente total m1Não. m_{1}} está previsto para ter sido m1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =5.41+2.5.)) 3.69)) log10.⁡ ⁡ (0.302)+5log10.⁡ ⁡ (1.109)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =+0Não. m_{1}=5.41+2.5cdot 3.69cdot log _{10}{left(0.302right)}+5log _{10}{left(1.109right)}=+0.8} naquela altura. O Minor Planet Center dá um valor próximo a isso, m1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =+0,5Não. M_{1}=+0.5}.

magnitudes absolutas e tamanhos de núcleos de cometa

Comet	Absoluta magnitude M1Não. M_{1}}	Nucleus diâmetro
Cometa Sarabat	-3.0	- 100 km?
Cometa Hale-Bopp	-1.3.	60 ± 20 km
Cometa Halley	4.0	14.9 x 8.2 km
média nova cometa	6.5	≈2 km
C/2014 UN271 (Bernardinelli-Bernstein)	6.7	60-200 km?
289P/Blanpain (durante 1819 explosão)	8.5	320 m
289P/Blanpain (atividade normal)	22.9	320 m

A magnitude absoluta de qualquer cometa pode variar dramaticamente. Pode mudar à medida que o cometa se torna mais ou menos ativo ao longo do tempo ou se passa por uma explosão. Isso torna difícil usar a magnitude absoluta para uma estimativa de tamanho. Quando o cometa 289P/Blanpain foi descoberto em 1819, sua magnitude absoluta foi estimada como M1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =8.5Não. M_{1}=8.5}. Foi posteriormente perdido e só foi redescoberto em 2003. Naquela época, sua magnitude absoluta tinha diminuído para M1= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =22.9Não. M_{1}=22.9}, e foi percebido que a aparição de 1819 coincidiu com uma explosão. 289P/Blanpain alcançou brilho olho nu (5-8 mag) em 1819, embora seja o cometa com o menor núcleo que já foi fisicamente caracterizado, e geralmente não se torna mais brilhante do que 18 mag.

Para alguns cometas que foram observados em distâncias heliocêntricas grandes o suficiente para distinguir entre a luz refletida do coma e a luz do próprio núcleo, uma magnitude absoluta análoga à usada para asteróides foi calculada, permitindo estimar os tamanhos de seus núcleos.

Meteoros

Para um meteoro, a distância padrão para medição de magnitudes é a uma altitude de 100 km (62 mi) no zênite do observador.