Linguagem formal

Estrutura da sintaticamente bem formada, embora não sensata, sentença inglesa, "Ideias verdes coloridas dormem furiosamente" (exemplo histórico de Chomsky 1957).

Em lógica, matemática, ciência da computação e lingüística, uma linguagem formal consiste em palavras cujas letras são retiradas de um alfabeto e são bem formadas de acordo com um conjunto específico de regras.

O alfabeto de uma linguagem formal consiste em símbolos, letras ou tokens que se concatenam em strings da linguagem. Cada string concatenada de símbolos desse alfabeto é chamada de palavra, e as palavras que pertencem a uma linguagem formal particular são às vezes chamadas de palavras bem formadas ou fórmulas bem formadas. Uma linguagem formal é muitas vezes definida por meio de uma gramática formal, como uma gramática regular ou gramática livre de contexto, que consiste em suas regras de formação.

Na ciência da computação, as linguagens formais são usadas, entre outras, como base para definir a gramática de linguagens de programação e versões formalizadas de subconjuntos de linguagens naturais nas quais as palavras da linguagem representam conceitos associados a significados ou semânticas particulares. Na teoria da complexidade computacional, os problemas de decisão são tipicamente definidos como linguagens formais, e as classes de complexidade são definidas como os conjuntos de linguagens formais que podem ser analisadas por máquinas com poder computacional limitado. Na lógica e nos fundamentos da matemática, as linguagens formais são usadas para representar a sintaxe dos sistemas axiomáticos, e o formalismo matemático é a filosofia de que toda a matemática pode ser reduzida à manipulação sintática de linguagens formais dessa maneira.

O campo da teoria da linguagem formal estuda principalmente os aspectos puramente sintáticos de tais linguagens - isto é, seus padrões estruturais internos. A teoria da linguagem formal surgiu da lingüística, como uma forma de entender as regularidades sintáticas das línguas naturais.

História

No século XVII, Gottfried Leibniz imaginou e descreveu a caracteristica universalis, uma linguagem universal e formal que utilizava pictogramas. Durante este período, Carl Friedrich Gauss também investigou o problema dos códigos de Gauss.

Gottlob Frege tentou concretizar as ideias de Leibniz, através de um sistema de notação delineado pela primeira vez em Begriffsschrift (1879) e mais desenvolvido em seus 2 volumes Grundgesetze der Arithmetik (1893/1903). Isso descrevia uma "linguagem formal de linguagem pura."

Na primeira metade do século XX, vários desenvolvimentos foram feitos com relevância para as linguagens formais. Axel Thue publicou quatro artigos relacionados a palavras e linguagem entre 1906 e 1914. O último deles introduziu o que Emil Post mais tarde denominou 'Thue Systems' e deu um exemplo inicial de um problema indecidível. Post usaria mais tarde este artigo como base para uma prova de 1947 “de que o problema de palavras para semigrupos era recursivamente insolúvel” e, posteriormente, concebeu o sistema canônico para a criação de linguagens formais.

Noam Chomsky concebeu uma representação abstrata das linguagens formais e naturais, conhecida como a hierarquia de Chomsky. Em 1959, John Backus desenvolveu a forma Backus-Naur para descrever a sintaxe de uma linguagem de programação de alto nível, seguindo seu trabalho na criação do FORTRAN. Peter Naur inventou um esquema semelhante em 1960.

Palavras sobre um alfabeto

Um alfabeto, no contexto das linguagens formais, pode ser qualquer conjunto, embora muitas vezes faça sentido usar um alfabeto no sentido usual da palavra, ou mais geralmente qualquer codificação de caracteres finitos como como ASCII ou Unicode. Os elementos de um alfabeto são chamados de letras. Um alfabeto pode conter um número infinito de elementos; no entanto, a maioria das definições na teoria da linguagem formal especifica alfabetos com um número finito de elementos, e a maioria dos resultados se aplica apenas a eles.

Uma palavra sobre um alfabeto pode ser qualquer sequência finita (ou seja, string) de letras. O conjunto de todas as palavras sobre um alfabeto Σ é geralmente denotado por Σ^* (usando a estrela Kleene). O comprimento de uma palavra é o número de letras que a compõem. Para qualquer alfabeto, existe apenas uma palavra de comprimento 0, a palavra vazia, que geralmente é denotada por e, ε, λ ou mesmo Λ. Por concatenação pode-se combinar duas palavras para formar uma nova palavra, cujo comprimento é a soma dos comprimentos das palavras originais. O resultado da concatenação de uma palavra com a palavra vazia é a palavra original.

Em algumas aplicações, especialmente em lógica, o alfabeto também é conhecido como vocabulário e as palavras são conhecidas como fórmulas ou frases; isso quebra a metáfora da letra/palavra e a substitui por uma metáfora da palavra/frase.

Definição

Uma linguagem formal L sobre um alfabeto Σ é um subconjunto de Σ^*, ou seja, um conjunto de palavras sobre esse alfabeto. Às vezes, os conjuntos de palavras são agrupados em expressões, enquanto regras e restrições podem ser formuladas para a criação de 'expressões bem formadas'.

Em ciência da computação e matemática, que geralmente não lidam com linguagens naturais, o adjetivo "formal" é frequentemente omitido por ser redundante.

Embora a teoria da linguagem formal geralmente se preocupe com linguagens formais que são descritas por algumas regras sintáticas, a definição real do conceito "linguagem formal" é apenas como acima: um conjunto (possivelmente infinito) de cadeias de comprimento finito compostas de um determinado alfabeto, nem mais nem menos. Na prática, existem muitas linguagens que podem ser descritas por regras, como linguagens regulares ou linguagens livres de contexto. A noção de uma gramática formal pode estar mais próxima do conceito intuitivo de uma "língua" um descrito por regras sintáticas. Por um abuso da definição, uma linguagem formal particular é muitas vezes pensada como sendo equipada com uma gramática formal que a descreve.

Exemplos

As seguintes regras descrevem uma linguagem formal L sobre o alfabeto Σ = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, +, =}:

• Cada string que não contém "+" ou "=" e não começa com "0" está emL.
• A string "0" está emL.
• Uma string contendo "=" está emL se e somente se houver exatamente um "=", e ele separa duas cadeias válidas deL.
• Uma string contendo "+" mas não "=" está emL se e somente se cada "+" na string separar duas cadeias válidas deL.
• Nenhuma string está dentroL outros que os implícitos pelas regras anteriores.

Sob essas regras, a string "23+4=555" está em L, mas a string "=234=+" não é. Essa linguagem formal expressa números naturais, adições bem formadas e igualdades de adição bem formadas, mas expressa apenas sua aparência (sua sintaxe), não o que significam (semântica). Por exemplo, em nenhum lugar dessas regras há qualquer indicação de que "0" significa o número zero, "+" significa adição, "23+4=555" é falso, etc

Construções

Para linguagens finitas, pode-se enumerar explicitamente todas as palavras bem formadas. Por exemplo, podemos descrever um idioma L apenas como L = {a, b, ab, cba}. O caso degenerado dessa construção é a linguagem vazia, que não contém nenhuma palavra (L = ∅).

No entanto, mesmo em um alfabeto finito (não vazio), como Σ = {a, b}, há um número infinito de palavras de comprimento finito que podem ser expressas potencialmente: "a", & #34;abb", "ababba", "aaababbbbaab",.... Portanto, linguagens formais são tipicamente infinitas, e descrever uma linguagem formal infinita não é tão simples quanto escrever L = {a, b, ab, cba}. Aqui estão alguns exemplos de linguagens formais:

• L = Σ^*, o conjunto de Todos palavras sobre Σ;
• L Não.^* =ⁿOnde? n varia sobre os números naturais e "aⁿ" significa "um" repetido n tempos (este é o conjunto de palavras que consistem apenas do símbolo "a");
• o conjunto de programas sinteticamente corretos em uma determinada linguagem de programação (a sintaxe da qual é geralmente definida por uma gramática livre de contexto);
• o conjunto de entradas em que uma determinada máquina de Turing para; ou
• o conjunto de cordas máximas de caracteres ASCII alfanuméricos nesta linha, ou seja,
  o conjunto {o, conjunto, de, maximal, strings, alfanumérico, ASCII, caracteres, on, this, line, i, e}.

Formalismos de especificação de linguagem

As linguagens formais são usadas como ferramentas em várias disciplinas. No entanto, a teoria da linguagem formal raramente se preocupa com línguas particulares (exceto como exemplos), mas se preocupa principalmente com o estudo de vários tipos de formalismos para descrever línguas. Por exemplo, uma língua pode ser dada como

• aquelas cordas geradas por alguma gramática formal;
• essas cadeias descritas ou combinadas por uma expressão regular particular;
• essas cordas aceitas por algum autômato, como uma máquina de Turing ou um autômato de estado finito;
• aquelas cadeias para as quais algum procedimento de decisão (um algoritmo que faz uma sequência de perguntas relacionadas YES/NO) produz a resposta SIM.

Perguntas típicas feitas sobre tais formalismos incluem:

• Qual é o seu poder expressivo? (Pode formalismo X descrever cada linguagem que o formalismo Y pode descrever? Pode descrever outras línguas?)
• Qual é a sua capacidade de reconhecimento? (Quão difícil é decidir se uma determinada palavra pertence a uma linguagem descrita pelo formalismo X?)
• Qual é a sua comparabilidade? (Quão difícil é decidir se duas línguas, uma descrita no formalismo X e um no formalismo You dentro X novamente, são realmente a mesma língua?).

Surpreendentemente, a resposta para esses problemas de decisão é "isso não pode ser feito" ou "é extremamente caro" (com uma caracterização de quão caro). Portanto, a teoria da linguagem formal é uma importante área de aplicação da teoria da computabilidade e da teoria da complexidade. As línguas formais podem ser classificadas na hierarquia de Chomsky com base no poder expressivo de sua gramática gerativa, bem como na complexidade de seu autômato de reconhecimento. Gramáticas livres de contexto e gramáticas regulares fornecem um bom compromisso entre expressividade e facilidade de análise e são amplamente usadas em aplicações práticas.

Operações em idiomas

Certas operações em idiomas são comuns. Isso inclui as operações de conjunto padrão, como união, interseção e complemento. Outra classe de operação é a aplicação element-wise de operações de string.

Exemplos: L1{displaystyle L_{1}} e L2{displaystyle L_{2}} são línguas sobre algum alfabeto comum Σ Σ Não. Sim..

• O concatenação L1)) L2{displaystyle L_{1}cdot L_{2}} consiste em todas as cadeias do formulário vO quê?Não. Onde? vNão. é uma string de L1{displaystyle L_{1}} e O quê?Não. é uma string de L2{displaystyle L_{2}}.
• O interseção L1─ ─ L2{displaystyle L_{1}cap L_{2}} de L1{displaystyle L_{1}} e L2{displaystyle L_{2}} consiste em todas as cadeias que estão contidas em ambos os idiomas
• O complemento ? ? L1{displaystyle neg L_{1}} de L1{displaystyle L_{1}} com respeito a Σ Σ Não. Sim. consiste em todas as cadeias de caracteres Σ Σ Não. Sim. que não estão dentro L1{displaystyle L_{1}}.
• A estrela Kleene: a linguagem que consiste em todas as palavras que são concatenações de zero ou mais palavras na língua original;
• Reversões:
  • Vamos. ε ser a palavra vazia, então ε ε R= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =ε ε {displaystyle varepsilon ^{R}=varepsilon }e
  • para cada palavra não vazia O quê?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =σ σ 1⋯ ⋯ σ σ n{displaystyle w=sigma _{1}cdots sigma _{n}} (onde) σ σ 1,...... ,σ σ n{displaystyle sigma _{1},ldotssigma _{n}}são elementos de algum alfabeto), let O quê?R= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =σ σ n⋯ ⋯ σ σ 1{displaystyle w^{R}=sigma _{n}cdots sigma _{1}},
  • então para uma linguagem formal LNão. L., LR= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(O quê?R∣ ∣ O quê?∈ ∈ L?Não. L^{R}={w^{R}mid win L}}.
• Homomorfismo de corda

Essas operações de string são usadas para investigar propriedades de fechamento de classes de linguagens. Uma classe de linguagens é fechada sob uma determinada operação quando a operação, aplicada às linguagens da classe, sempre produz novamente uma linguagem da mesma classe. Por exemplo, as linguagens livres de contexto são conhecidas por serem fechadas sob união, concatenação e interseção com linguagens regulares, mas não fechadas sob interseção ou complemento. A teoria dos trios e famílias abstratas de línguas estuda as propriedades de fechamento mais comuns das famílias de línguas por direito próprio.

Closure properties of language families ( L 1 {displaystyle L_{1}} Op L 2 {displaystyle L_{2}} where both L 1 {displaystyle L_{1}} and L 2 {displaystyle L_{2}} are in the language family given by the column). After Hopcroft and Ullman.

Operation		Regular	DCFL	CFL	IND	CSL	recursive	RE
Union	L 1 ∪ L 2 = { w ∣ w ∈ L 1 ∨ w ∈ L 2 } {displaystyle L_{1}cup L_{2}={wmid win L_{1}lor win L_{2}}}	Yes	No	Yes	Yes	Yes	Yes	Yes
Intersection	L 1 ∩ L 2 = { w ∣ w ∈ L 1 ∧ w ∈ L 2 } {displaystyle L_{1}cap L_{2}={wmid win L_{1}land win L_{2}}}	Yes	No	No	No	Yes	Yes	Yes
Complement	¬ L 1 = { w ∣ w ∉ L 1 } {displaystyle neg L_{1}={wmid wnot in L_{1}}}	Yes	Yes	No	No	Yes	Yes	No
Concatenation	L 1 ⋅ L 2 = { w z ∣ w ∈ L 1 ∧ z ∈ L 2 } {displaystyle L_{1}cdot L_{2}={wzmid win L_{1}land zin L_{2}}}	Yes	No	Yes	Yes	Yes	Yes	Yes
Kleene star	L 1 ∗ = { ε } ∪ { w z ∣ w ∈ L 1 ∧ z ∈ L 1 ∗ } {displaystyle L_{1}^{*}={varepsilon }cup {wzmid win L_{1}land zin L_{1}^{*}}}	Yes	No	Yes	Yes	Yes	Yes	Yes
(String) homomorphism h {displaystyle h}	h ( L 1 ) = { h ( w ) ∣ w ∈ L 1 } {displaystyle h(L_{1})={h(w)mid win L_{1}}}	Yes	No	Yes	Yes	No	No	Yes
ε-free (string) homomorphism h {displaystyle h}	h ( L 1 ) = { h ( w ) ∣ w ∈ L 1 } {displaystyle h(L_{1})={h(w)mid win L_{1}}}	Yes	No	Yes	Yes	Yes	Yes	Yes
Substitution φ {displaystyle varphi }	φ ( L 1 ) = ⋃ σ 1 ⋯ σ n ∈ L 1 φ ( σ 1 ) ⋅ … ⋅ φ ( σ n ) {displaystyle varphi (L_{1})=bigcup _{sigma _{1}cdots sigma _{n}in L_{1}}varphi (sigma _{1})cdot ldots cdot varphi (sigma _{n})}	Yes	No	Yes	Yes	Yes	No	Yes
Inverse homomorphism h − 1 {displaystyle h^{-1}}	h − 1 ( L 1 ) = ⋃ w ∈ L 1 h − 1 ( w ) {displaystyle h^{-1}(L_{1})=bigcup _{win L_{1}}h^{-1}(w)}	Yes	Yes	Yes	Yes	Yes	Yes	Yes
Reverse	L R = { w R ∣ w ∈ L } {displaystyle L^{R}={w^{R}mid win L}}	Yes	No	Yes	Yes	Yes	Yes	Yes
Intersection with a regular language R {displaystyle R}	L ∩ R = { w ∣ w ∈ L ∧ w ∈ R } {displaystyle Lcap R={wmid win Lland win R}}	Yes	Yes	Yes	Yes	Yes	Yes	Yes

Aplicativos

Linguagens de programação

Um compilador geralmente tem dois componentes distintos. Um analisador léxico, às vezes gerado por uma ferramenta como lex, identifica os tokens da gramática da linguagem de programação, por exemplo identificadores ou palavras-chave, literais numéricos e de string, pontuação e símbolos de operador, que são especificados por uma linguagem formal mais simples, geralmente por meio de expressões regulares. No nível conceitual mais básico, um parser, às vezes gerado por um gerador de parser como yacc, tenta decidir se o programa fonte é sintaticamente válido, ou seja, se está bem formado em relação à linguagem de programação gramática para a qual o compilador foi construído.

É claro que os compiladores fazem mais do que apenas analisar o código-fonte – eles geralmente o traduzem em algum formato executável. Por causa disso, um analisador geralmente produz mais do que uma resposta sim/não, geralmente uma árvore de sintaxe abstrata. Isso é usado pelos estágios subsequentes do compilador para eventualmente gerar um executável contendo código de máquina que é executado diretamente no hardware ou algum código intermediário que requer uma máquina virtual para ser executado.

Teorias, sistemas e provas formais

Este diagrama mostra as divisões sintáticas dentro de um sistema formal. As cordas de símbolos podem ser amplamente divididas em fórmulas absurdas e bem formadas. O conjunto de fórmulas bem formadas é dividido em teoremas e não teoremas.

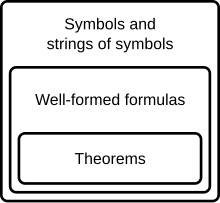
Na lógica matemática, uma teoria formal é um conjunto de sentenças expressas em uma linguagem formal.

A sistema formal (também chamado de cálculo lógicoou um sistema lógico) consiste em uma linguagem formal junto com um aparelho dedutivo (também chamado de sistema de dedução). O aparelho dedutivo pode consistir em um conjunto de regras de transformação, que podem ser interpretadas como regras válidas de inferência, ou um conjunto de axiomas, ou têm ambos. Um sistema formal é usado para derivar uma expressão de uma ou mais outras expressões. Embora uma linguagem formal possa ser identificada com suas fórmulas, um sistema formal não pode ser igualmente identificado por seus teoremas. Dois sistemas formais FS{displaystyle {mathcal {FS}}} e FS?{displaystyle {mathcal {FS'}}} pode ter todos os mesmos teoremas e ainda diferem de alguma forma significativa de prova-teórico (uma fórmula A pode ser uma consequência sintática de uma fórmula B em um, mas não outro, por exemplo).

Uma prova formal ou derivação é uma sequência finita de fórmulas bem formadas (que podem ser interpretadas como sentenças ou proposições), cada uma das quais é um axioma ou segue das fórmulas anteriores na sequência por uma regra de inferência. A última frase da sequência é um teorema de um sistema formal. Provas formais são úteis porque seus teoremas podem ser interpretados como proposições verdadeiras.

Interpretações e modelos

As linguagens formais são inteiramente sintáticas por natureza, mas podem receber semânticas que dão significado aos elementos da linguagem. Por exemplo, na lógica matemática, o conjunto de possíveis fórmulas de uma determinada lógica é uma linguagem formal, e uma interpretação atribui um significado a cada uma das fórmulas – geralmente, um valor de verdade.

O estudo das interpretações de linguagens formais é chamado de semântica formal. Na lógica matemática, isso geralmente é feito em termos de teoria de modelos. Na teoria dos modelos, os termos que ocorrem em uma fórmula são interpretados como objetos dentro de estruturas matemáticas, e as regras fixas de interpretação composicional determinam como o valor verdadeiro da fórmula pode ser derivado da interpretação de seus termos; um modelo para uma fórmula é uma interpretação dos termos de modo que a fórmula se torne verdadeira.