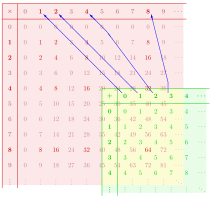
Homomorfismo
Na álgebra, um homomorfismo é um mapa de preservação de estrutura entre duas estruturas algébricas do mesmo tipo (como dois grupos, dois anéis ou dois espaços vetoriais). A palavra homomorfismo vem da língua grega antiga: ὁμός (homos) que significa "o mesmo" e μορφή (morfo) que significa "forma" ou "forma". No entanto, a palavra foi aparentemente introduzida na matemática devido a uma (errada) tradução do alemão ähnlich que significa "semelhante" para ὁμός que significa "o mesmo". O termo "homomorfismo" apareceu já em 1892, quando foi atribuído ao matemático alemão Felix Klein (1849-1925).
Os homomorfismos de espaços vetoriais também são chamados de mapas lineares, e seu estudo é objeto de álgebra linear.
O conceito de homomorfismo foi generalizado, sob o nome de morfismo, para muitas outras estruturas que não possuem um conjunto subjacente ou não são algébricas. Essa generalização é o ponto de partida da teoria das categorias.
Um homomorfismo também pode ser um isomorfismo, um endomorfismo, um automorfismo, etc. (veja abaixo). Cada um deles pode ser definido de uma forma que pode ser generalizada para qualquer classe de morfismos.
Definição
Um homomorfismo é um mapa entre duas estruturas algébricas do mesmo tipo (isto é do mesmo nome), que preserva as operações das estruturas. Isto significa um mapa entre dois conjuntos , equipado com a mesma estrutura tal que, se é uma operação da estrutura (suposta aqui, para simplificação, para ser uma operação binária), então
para cada par , de elementos de . Um diz muitas vezes que preserva a operação ou é compatível com a operação.
Formalmente, um mapa preserva uma operação de aridade , definido em ambos e se
para todos os elementos em .
As operações que devem ser preservadas por um homomorfismo incluem operações 0-árias, ou seja, as constantes. Em particular, quando um elemento de identidade é requerido pelo tipo de estrutura, o elemento de identidade da primeira estrutura deve ser mapeado para o elemento de identidade correspondente da segunda estrutura.
Por exemplo:
- Um homomorfismo semigrupo é um mapa entre semigrupos que preserva a operação do semigrupo.
- Um homomorfismo monoide é um mapa entre monoídeos que preserva a operação monoide e mapeia o elemento de identidade do primeiro monoide ao do segundo monoide (o elemento de identidade é uma operação de 0-ary).
- Um homomorfismo de grupo é um mapa entre grupos que preserva a operação do grupo. Isso implica que o homomorfismo do grupo mapeia o elemento de identidade do primeiro grupo para o elemento de identidade do segundo grupo, e mapeia o inverso de um elemento do primeiro grupo para o inverso da imagem deste elemento. Assim, um homomorfismo semigrupo entre grupos é necessariamente um homomorfismo de grupo.
- Um homomorfismo do anel é um mapa entre anéis que preserva a adição do anel, a multiplicação do anel e a identidade multiplicativa. Se a identidade multiplicativa deve ser preservada depende da definição de anel em uso. Se a identidade multiplicativa não é preservada, tem-se um homomorfismo rng.
- Um mapa linear é um homomorfismo de espaços vetoriais; isto é, um homomorfismo de grupo entre espaços vetoriais que preserva a estrutura do grupo abeliano e a multiplicação escalar.
- Um homomorfismo de módulo, também chamado de mapa linear entre módulos, é definido de forma semelhante.
- Um homomorfismo de álgebra é um mapa que preserva as operações de álgebra.
Uma estrutura algébrica pode ter mais de uma operação, e um homomorfismo é necessário para preservar cada operação. Assim, um mapa que preserva apenas algumas das operações não é um homomorfismo da estrutura, mas apenas um homomorfismo da subestrutura obtido considerando apenas as operações preservadas. Por exemplo, um mapa entre monóides que preserva a operação monóide e não o elemento identidade, não é um homomorfismo monoide, mas apenas um homomorfismo de semigrupo.
A notação para as operações não precisa ser a mesma na origem e no destino de um homomorfismo. Por exemplo, os números reais formam um grupo para adição e os números reais positivos formam um grupo para multiplicação. A função exponencial
satisfaz
e é, portanto, um homomorfismo entre esses dois grupos. É até um isomorfismo (veja abaixo), pois sua função inversa, o logaritmo natural, satisfaz
e também é um homomorfismo de grupo.
Exemplos
Os números reais são um anel, tendo adição e multiplicação. O conjunto de todas as matrizes 2 × 2 também é um anel, sob adição de matrizes e multiplicação de matrizes. Se definirmos uma função entre esses anéis da seguinte forma:
Contenido relacionado
Jorge Dantzig
Oito rainhas quebra-cabeça
Alexander Anderson (matemático)