Hexadecimal
Na matemática e na computação, o sistema numérico hexadecimal (também base-16 ou simplesmente hex) é um sistema numérico posicional que representa números usando uma raiz (base) de 16. Ao contrário do sistema decimal que representa números usando 10 símbolos, o hexadecimal usa 16 símbolos distintos, na maioria das vezes os símbolos "0"–"9" para representar os valores de 0 a 9, e "A"–"F" (ou alternativamente "a"–"f") para representar valores de 10 a 15.
Desenvolvedores de software e projetistas de sistemas usam amplamente números hexadecimais porque fornecem uma representação amigável de valores codificados em binário. Cada dígito hexadecimal representa quatro bits (dígitos binários), também conhecidos como nibble (ou nybble). Por exemplo, um byte de 8 bits pode ter valores variando de 00000000 a 11111111 na forma binária, que pode ser convenientemente representado como 00 a FF em hexadecimal.
Na matemática, um subscrito é normalmente usado para especificar a base. Por exemplo, o valor decimal 18.050 seria expresso em hexadecimal como 468216. Na programação, várias notações são usadas para denotar números hexadecimais, geralmente envolvendo um prefixo. O prefixo 0x é usado em C, o que denotaria esse valor como 0x4682.
Hexadecimal é usado na codificação de transferência Base16, na qual cada byte do texto simples é dividido em dois valores de 4 bits e representado por dois dígitos hexadecimais.
Representação
Representação escrita
Na maioria dos casos de uso atuais, as letras A–F ou a–f representam os valores 10–15, enquanto os numerais 0–9 são usados para representar seus valores decimais.
Não existe uma convenção universal para usar letras minúsculas ou maiúsculas, então cada uma prevalece ou é preferida em ambientes particulares por padrões ou convenções da comunidade; até caso misto é usado. Displays de sete segmentos usam AbCdEF caso misto para fazer dígitos que podem ser distinguidos uns dos outros.
Existe alguma padronização no uso de espaços (em vez de vírgulas ou outro sinal de pontuação) para separar valores hexadecimais em uma longa lista. Por exemplo, no dump hexadecimal a seguir, cada byte de 8 bits é um número hexadecimal de 2 dígitos, com espaços entre eles, enquanto o deslocamento de 32 bits no início é um número hexadecimal de 8 dígitos.
- Não. 57 69 6b 69 70 65 64 69 61 2c 20. 74 68 65 20. 66 000 milhões de euros 72 65 65 20. 65 6 63 79 63 6c 6f 70 65 64 69 61 000 milhões de euros 20. 74 68 61 74 20. 61 6 79 6f 6 65 20. 63 61 6 000 milhões de euros 20. 65 64 69 74 0aDiferenciação de decimal
Em contextos onde a base não é clara, os números hexadecimais podem ser ambíguos e confundidos com números expressos em outras bases. Existem várias convenções para expressar valores de forma inequívoca. Um subscrito numérico (ele próprio escrito em decimal) pode fornecer a base explicitamente: 15910 é decimal 159; 15916 é hexadecimal 159, que é igual a 34510. Alguns autores preferem um subscrito de texto, como 159decimal e 159hex, ou 159d e 159h.
Donald Knuth introduziu o uso de um tipo de letra específico para representar uma raiz específica em seu livro The TeXbook. As representações hexadecimais são escritas em um tipo de máquina de escrever: 5A3
Em sistemas de texto linear, como os usados na maioria dos ambientes de programação de computadores, surgiram vários métodos:
- Unix (e relacionados) shells, linguagem de montagem AT&T e também a linguagem de programação C (e seus descendentes sintáticos, como C++, C#, Go, D, Java, JavaScript, Python e Windows PowerShell) usam o prefixo
0xpara constantes numéricas representadas no hex:0x5A3. Constantes de caracteres e string podem expressar códigos de caracteres em hexadecimal com o prefixoxseguido por dois dígitos hex:'x1B'representa o caráter de controle Esc;"x1B[0mx1B[25;1H"é uma string contendo 11 caracteres com dois caracteres Esc incorporados. Para produzir um inteiro como hexadecimal com a família de função printf, o código de conversão de formato%Xou%xé usado. - Em URIs (incluindo URLs), os códigos de caracteres são escritos como pares hexadecimais prefixados com
%:http://www.example.com/name%20with%20spacesOnde?%20é o código para o caractere espaço (blank), código ASCII ponto 20 em hex, 32 em decimal. - Em XML e XHTML, os caracteres podem ser expressos como referências numéricas hexadecimais usando a notação
ode;, por exemplo’representa o caractere U+2019 (a marca de cotação única direita). Se não houverxo número é decimal (thus’é o mesmo personagem). - No padrão Unicode, um valor de caractere é representado com
U+seguido pelo valor hex, por exemplo.U+20ACé o sinal Euro (€). - As referências de cores em HTML, CSS e X Window podem ser expressas com seis dígitos hexadecimais (dois cada um para os componentes vermelhos, verdes e azuis, nessa ordem) prefixados com
#: branco, por exemplo, é representado como#FFFFFF. CSS também permite abreviações de 3 dígitos com um hexdigit por componente: #FA3 abrevia #FFA33 (uma laranja dourada: ). - Em MIME (extensões de e-mail) codificação citável, os códigos de caracteres são escritos como pares hexadecimais prefixados com
=:Espa=F1aé "España" (F1 é o código para ñ no conjunto de caracteres ISO/IEC 8859-1).) - Em linguagens de montagem derivadas da Intel e Modula-2, o hexadecimal é denotado com um sufixo H. H. H. ou h:
FFhou05A3H. Algumas implementações requerem um zero líder quando o primeiro caractere hexadecimal de dígitos não é um dígito decimal, então um escreveria0FFhem vez deFFh. Algumas outras implementações (como NASM) permitem números de estilo C (0x42). - Outras linguagens de montagem (6502, Motorola), Pascal, Delphi, algumas versões de BASIC (Commodore), GameMaker Language, Godot e Forth use
$como um prefixo:$5A3. - Algumas linguagens de montagem (Microchip) usam a notação
H'ABCD'(para ABCD16.). Da mesma forma, Fortran 95 usa Z'ABCD'. - Ada e VHDL encerram numerais hexadecimais em "citações numéricas" baseadas:
16#5A3#. Para constantes vetoriais bits VHDL usa a notaçãox"5A3". - Verilog representa constantes hexadecimais na forma
8'hFF, onde 8 é o número de bits no valor e FF é a constante hexadecimal. - A língua Smalltalk usa o prefixo
16r:16r5A3 - PostScript e o Bourne shell e seus derivados denote hex com prefixo
16#:16#5A3. Para o PostScript, dados binários (como pixels de imagem) podem ser expressos como pares hexadecimais consecutivos não pré-fixados:AA213FD51B3801043FBC... - Lisp comum usa os prefixos
#xe#16r. Definir as variáveis *read-base* e *print-base* a 16 também pode ser usado para mudar o leitor e a impressora de um sistema de Lisp Comum para a representação de números hexadecimais para leitura e impressão. Assim, os números hexadecimais podem ser representados sem o código de prefixo #x ou #16r, quando a base de entrada ou saída foi alterada para 16. - MSX BASIC, QuickBASIC, FreeBASIC e Visual Basic prefixo números hexadecimais com
&H:&H5A3 - BBC BASIC e utilização locomotiva BASIC
&por hex. - Série TI-89 e 92 usa uma
0hPrefixo:0h5A3 - ALGOL 68 usa o prefixo
16rpara denotar números hexadecimais:16r5a3. Os números binários, quaternários (base-4) e octal podem ser especificados de forma semelhante. - O formato mais comum para hexadecimal em mainframes da IBM (zSeries) e computadores midrange (IBM i) executando o sistema operacional tradicional (zOS, zVSE, zVM, TPF, IBM i) é
X'5A3', e é usado em Assembler, PL/I, COBOL, JCL, scripts, comandos e outros lugares. Este formato era comum em outros sistemas (e agora obsoletos) IBM também. Ocasionalmente aspas foram usadas em vez de apostrofes. - Qualquer endereço IPv6 pode ser escrito como oito grupos de quatro dígitos hexadecimais (às vezes chamados hextetos), onde cada grupo é separado por um cólon (
:). Este, por exemplo, é um endereço IPv6 válido:2001:0db8:85a3:0000:0000:8a2e:0370:7334ou abreviado removendo zeros como2001:db8:85a3::8a2e:370:7334(Os endereços IPv4 são geralmente escritos em decimal). - Identificadores globalmente únicos são escritos como trinta e dois dígitos hexadecimais, muitas vezes em agrupamentos separados por hífen desiguais, por exemplo
3F2504E0-4F89-41D3-9A0C-0305E82C3301.
Outros símbolos para 10–15 e principalmente conjuntos de símbolos diferentes
O uso das letras A a F para representar os dígitos acima de 9 não era universal no início da história dos computadores.
- Durante a década de 1950, algumas instalações, como Bendix-14, favoreceram o uso dos dígitos 0 a 5 com uma linha para denotar os valores 10-15 como 0, 1, 2, 3, 4 e 5.
- Os computadores SWAC (1950) e Bendix G-15 (1956) usaram letras minúsculas u, v, O quê?, x, Sim. e zangão. para os valores 10 a 15.
- Os computadores ORDVAC e ILLIAC I (1952) (e alguns desenhos derivados, por exemplo BRLESC) usaram as letras maiúsculas KK, S, N, JJ, F e L para os valores 10 a 15.
- O Librascope LGP-30 (1956) usou as letras F, G, JJ, KK, Q e W para os valores 10 a 15.
- No computador PERM (1956) os números hexadecimais foram escritos como letras O para zero, A para N e P para 1 a 15. Muitas instruções da máquina tinham códigos hexônicos mnemônicos (A- A sério? M- Multiplica, L- carga, F=fixed-point etc.); programas foram escritos sem nomes de instrução.
- O Honeywell Datamatic D-1000 (1957) usou as letras minúsculas b), c, D, e, fe g Considerando que o Elbit 100 (1967) usou as letras maiúsculas B, C, D, E, F e G para os valores 10 a 15.
- O Monrobot XI (1960) usou as letras S, T, U, V, W e X para os valores 10 a 15.
- O computador parametron NEC NEAC 1103 (1960) usou as letras D, G, H. H. H., JJ, KK (e possivelmente) V) para valores 10-15.
- O Pacific Data Systems 1020 (1964) usou as letras L, C, A, S, M e D para os valores 10 a 15.
- Bruce Alan Martin, do Laboratório Nacional Brookhaven, considerou a escolha de A-F "ridiculous". Em uma carta de 1968 ao editor do CACM, ele propôs um conjunto inteiramente novo de símbolos com base nos locais de bits.
- Novos símbolos numéricos e nomes foram introduzidos na notação bibibinária de Boby Lapointe em 1968.
- Ronald O. Whitaker da Rowco Engineering Co., em 1972, propôs uma fonte triangular que permite "leitura binária direta" a fim de "permitir entrada e saída de computadores sem respeito à codificação matrizes".
- Alguns chips de decodificador de exibição de sete segmentos (ou seja, 74LS47) mostram saída inesperada devido à lógica projetada apenas para produzir 0-9 corretamente.
Representações verbais e digitais
Como não havia numerais tradicionais para representar as quantidades de dez a quinze, as letras alfabéticas foram reempregadas como um substituto. A maioria dos idiomas europeus carece de palavras não decimais para alguns dos numerais de onze a quinze. Algumas pessoas lêem números hexadecimais dígito por dígito, como um número de telefone, ou usando o alfabeto fonético da OTAN, o Alfabeto Fonético Conjunto do Exército/Marinha ou um sistema ad-hoc semelhante. Na esteira da adoção do hexadecimal entre os programadores do IBM System/360, Magnuson (1968) sugeriu um guia de pronúncia que dava nomes curtos às letras do hexadecimal – por exemplo, "A" pronunciava-se "ann", B "bet", C "chris", etc. Outro sistema de nomenclatura foi elaborado por Babb (2015), baseado em uma piada em Silicon Vale. Ainda outro sistema de nomenclatura foi publicado online por Rogers (2007) que tenta tornar a representação verbal distinguível em qualquer caso, mesmo quando o número real não contém os números A–F. Os exemplos estão listados nas tabelas abaixo.
Outros propuseram o uso das convenções verbais do Código Morse para expressar dígitos hexadecimais de quatro bits, com "dit" e "dah" representando zero e um, respectivamente, de modo que "0000" é dublado como "dit-dit-dit-dit" (....), dah-dit-dit-dah (-..-) expressa o dígito com um valor de nove e "dah-dah-dah-dah" (----) exprime o dígito hexadecimal para o decimal 15.
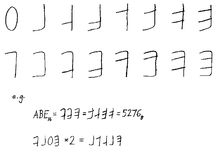
Sistemas de contagem de dígitos foram criados para binário e hexadecimal. Arthur C. Clarke sugeriu usar cada dedo como um bit liga/desliga, permitindo a contagem de zero a 102310 em dez dedos. Outro sistema de contagem até FF16 (25510) é ilustrado à direita.
| Número | Pronúncia |
|---|---|
| A | Anónimo |
| B | Aposta |
| C | Cristo! |
| D | Não. |
| E | O que é isto? |
| F | geada |
| 1A | Antenas |
| A0 | annty |
| 5B | 50-bet |
| A01C | annty christeen |
| 1AD0 | O que é isso? |
| 3A7D | 30-ann setenta-dot |
| Número | Pronúncia |
|---|---|
| A | dez. |
| B | onze |
| C | doze |
| D | draze |
| E | eptwin |
| F | fim |
| 10. | Tex |
| 11 | uma coisa |
| 1F | Não. |
| 50 | Fiftek |
| C0 | Twelftek |
| 100. | A sério? |
| 1000 | Tu |
| 3E | O que é isso? |
| E1 | eptek-one |
| C4A | 12hundrek-fourtek-ten |
| 1743 | um-thousek-seven- -hundrek-fourtek-three |
Sinais
O sistema hexadecimal pode expressar números negativos da mesma forma que em decimal: −2A para representar −4210 e assim por diante.
O hexadecimal também pode ser usado para expressar os padrões de bits exatos usados no processador, portanto, uma sequência de dígitos hexadecimais pode representar um valor com sinal ou até mesmo um valor de ponto flutuante. Dessa forma, o número negativo −4210 pode ser escrito como FFFF FFD6 em um registrador de CPU de 32 bits (em complemento de dois), como C228 0000 em um registrador de FPU de 32 bits ou C045 0000 0000 0000 em um registro FPU de 64 bits (no padrão de ponto flutuante IEEE).
Notação exponencial hexadecimal
Assim como os números decimais podem ser representados em notação exponencial, os números hexadecimais também podem. A notação P usa a letra P (ou p, para "potência"), enquanto E (ou e ) serve a um propósito semelhante na notação E decimal. O número após P é decimal e representa o expoente binário. Aumentar o expoente em 1 multiplica por 2, não por 16: 20p0 = 10p1 = 8p2 = 4p3 = 2p4 = 1,0p5. Normalmente, o número é normalizado para que os dígitos hexadecimais comecem com 1. (zero geralmente é 0 sem P ).
Exemplo: 1.3DEp42 representa 1.3DE16 × 24210.
A notação P é exigida pelo padrão binário de ponto flutuante IEEE 754-2008 e pode ser usada para literais de ponto flutuante na edição C99 da linguagem de programação C. Usando os especificadores de conversão %a ou %A, essa notação pode ser produzida por implementações da família de funções printf seguindo a especificação C99 e Especificação Unix única (IEEE Std 1003.1) Padrão POSIX.
Conversão
Conversão binária
A maioria dos computadores manipula dados binários, mas é difícil para os humanos trabalhar com um grande número de dígitos mesmo para um número binário relativamente pequeno. Embora a maioria das pessoas esteja familiarizada com o sistema de base 10, é muito mais fácil mapear binário para hexadecimal do que para decimal porque cada dígito hexadecimal é mapeado para um número inteiro de bits (410). Este exemplo converte 11112 na base dez. Como cada posição em um numeral binário pode conter 1 ou 0, seu valor pode ser facilmente determinado por sua posição à direita:
- 0002 = 110.
- 00102 = 210.
- 01002 = 410.
- 10002 = 810.
Portanto:
| 11112 | = 810. + 410. + 210. + 110. |
| = 1510. |
Com pouca prática, mapear 11112 para F16 em uma etapa torna-se fácil: veja a tabela na representação escrita. A vantagem de usar hexadecimal em vez de decimal aumenta rapidamente com o tamanho do número. Quando o número se torna grande, a conversão para decimal é muito tediosa. No entanto, ao mapear para hexadecimal, é trivial considerar a string binária como grupos de 4 dígitos e mapear cada um para um único dígito hexadecimal.
Este exemplo mostra a conversão de um número binário em decimal, mapeando cada dígito para o valor decimal e adicionando os resultados.
| (010111101011010010)2 | = 26214410. + 6553610. + 3276810. + 1638410. + 819210. + 204810. + 51210. + 25610. + 6410. + 1610. + 210. |
| = 38792210. |
Compare isso com a conversão para hexadecimal, onde cada grupo de quatro dígitos pode ser considerado independentemente e convertido diretamente:
| (010111101011010010)2 | = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = | 0101 | 1110 | 1011 | 0101 | 00102 |
| = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = | 5 | E | B | 5 | 216. | |
| = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = | 5EB5216. | |||||
A conversão de hexadecimal para binário é igualmente direta.
Outras conversões simples
Embora o quaternário (base 4) seja pouco usado, ele pode ser facilmente convertido de e para hexadecimal ou binário. Cada dígito hexadecimal corresponde a um par de dígitos quaternários e cada dígito quaternário corresponde a um par de dígitos binários. No exemplo acima, 5 E B 5 216 = 11 32 23 11 024.
O sistema octal (base 8) também pode ser convertido com relativa facilidade, embora não tão trivialmente quanto nas bases 2 e 4. Cada dígito octal corresponde a três dígitos binários, em vez de quatro. Portanto, podemos converter entre octal e hexadecimal por meio de uma conversão intermediária para binário, seguida do reagrupamento dos dígitos binários em grupos de três ou quatro.
Resto da divisão na base de origem
Tal como acontece com todas as bases, existe um algoritmo simples para converter uma representação de um número em hexadecimal fazendo operações de divisão inteira e resto na base de origem. Em teoria, isso é possível a partir de qualquer base, mas para a maioria dos humanos, apenas o decimal e para a maioria dos computadores, apenas o binário (que pode ser convertido por métodos muito mais eficientes) pode ser facilmente tratado com esse método.
Seja d o número a representar em hexadecimal, e a série hihi−1...h2h< sub>1 são os dígitos hexadecimais que representam o número.
- ← 1
- hEu... ← d mod 16
- d ← (d − hEu...) / 16
- Se d = 0 (retornar série hEu...) outro incremento i e ir para o passo 2
"16" pode ser substituído por qualquer outra base desejada.
O seguinte é uma implementação JavaScript do algoritmo acima para converter qualquer número em um hexadecimal na representação de String. Sua finalidade é ilustrar o algoritmo acima. Para trabalhar com dados a sério, no entanto, é muito mais aconselhável trabalhar com operadores bit a bit.
função Para Hex(D) ( var R = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = D % 16.; se (D - Não. R - Sim. 0) ( retorno para a Char(R); ? retorno Para Hex(D - Não. R) / 16.) + para a Char(R);?função para a Char(n) ( Não. alfa = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = "0123456789ABCDEF"; retorno alfa.CharAt(n);?Conversão por adição e multiplicação
Também é possível fazer a conversão atribuindo a cada local na base de origem a representação hexadecimal de seu valor posicional — antes de realizar a multiplicação e a adição para obter a representação final. Por exemplo, para converter o número B3AD para decimal, pode-se dividir o número hexadecimal em seus dígitos: B (1110), 3 (310), A (10 10) e D (1310) e obtenha o resultado final multiplicando cada representação decimal por 16p (p sendo a posição do dígito hexadecimal correspondente, contando da direita para a esquerda, começando com 0). Neste caso, temos que:
B3AD = (11 × 163) + (3 × 162) + (10 × 161< /sup>) + (13 × 160)
que é 45997 na base 10.
Ferramentas para conversão
Muitos sistemas de computador fornecem um utilitário de calculadora capaz de realizar conversões entre os vários radices frequentemente incluindo hexadecimal.
No Microsoft Windows, o utilitário Calculadora pode ser configurado no modo Programador, que permite conversões entre a raiz 16 (hexadecimal), 10 (decimal), 8 (octal) e 2 (binária), as bases mais usadas pelos programadores. No modo do programador, o teclado numérico na tela inclui os dígitos hexadecimais de A a F, que estão ativos quando "Hex" é selecionado. No modo hexadecimal, no entanto, a Calculadora do Windows suporta apenas números inteiros.
Aritmética elementar
Operações elementares como adição, subtração, multiplicação e divisão podem ser realizadas indiretamente por meio da conversão para um sistema numérico alternativo, como o sistema decimal comumente usado ou o sistema binário em que cada dígito hexadecimal corresponde a quatro dígitos binários.
Como alternativa, também é possível realizar operações elementares diretamente dentro do próprio sistema hexadecimal — contando com suas tabelas de adição/multiplicação e seus algoritmos padrão correspondentes, como a divisão longa e o algoritmo tradicional de subtração.
Números reais
Números racionais
Tal como acontece com outros sistemas numéricos, o sistema hexadecimal pode ser usado para representar números racionais, embora as expansões repetidas sejam comuns, pois dezesseis (1016) tem apenas um único fator primo; dois.
Para qualquer base, 0,1 (ou "1/10") é sempre equivalente a um dividido pela representação desse valor base em seu próprio sistema numérico. Portanto, seja dividindo um por dois para binário ou dividindo um por dezesseis para hexadecimal, ambas as frações são escritas como 0.1. Como a raiz 16 é um quadrado perfeito (42), as frações expressas em hexadecimal têm um período ímpar com muito mais frequência do que as decimais e não há números cíclicos (além de dígitos simples triviais). Dígitos recorrentes são exibidos quando o denominador em termos mais baixos tem um fator primo não encontrado na raiz; assim, ao usar a notação hexadecimal, todas as frações com denominadores que não são uma potência de dois resultam em uma sequência infinita de dígitos recorrentes (como terços e quintos). Isso torna hexadecimal (e binário) menos conveniente do que decimal para representar números racionais, uma vez que uma proporção maior fica fora de sua faixa de representação finita.
Todos os números racionais finitamente representáveis em hexadecimal também são finitamente representáveis em decimal, duodecimal e sexagesimal: ou seja, qualquer número hexadecimal com um número finito de dígitos também possui um número finito de dígitos quando expresso nessas outras bases. Por outro lado, apenas uma fração daqueles finitamente representáveis nas últimas bases são finitamente representáveis em hexadecimal. Por exemplo, o decimal 0.1 corresponde à representação recorrente infinita 0.19 em hexadecimal. No entanto, hexadecimal é mais eficiente que duodecimal e sexagesimal para representar frações com potência de dois no denominador. Por exemplo, 0,062510 (um décimo sexto) é equivalente a 0,116, 0,0912 e 0;3,4560 .
| n | Decimal Principais fatores de: base, b = 10: 2, 5; b) - 1 = 9: 3 | Hexadecimal Principais fatores de: base, b = 1610. = 10: 2; b − 1 = 1510. = F: 3, 5 | ||||
|---|---|---|---|---|---|---|
| Reciprocidade | Principais factores | Representação posicional (decimal) | Representação posicional (hexadecimal) | Principais factores | Reciprocidade | |
| 2 | 1/2-2001 | 2 | 0,5 | 0 | 2 | 1/2-2001 |
| 3 | 1/3 | 3 | 0.3333... 0.3 | 0.5555... 0.5 | 3 | 1/3 |
| 4 | 1/4 | 2 | 0,25 | 0 | 2 | 1/4 |
| 5 | 1/5 | 5 | 0,2 | 0.3 | 5 | 1/5 |
| 6 | 1/6 | 2, 3 | 0.16 | 0,2A | 2, 3 | 1/6 |
| 7 | 1/7 | 7 | 0.142857 | 0.249 | 7 | 1/7 |
| 8 | 1/8 | 2 | 0,125 | 0,2 | 2 | 1/8 |
| 9 | 1/9 | 3 | 0.1 | 0.1C7 | 3 | 1/9 |
| 10. | 1/10 | 2, 5 | 0.1 | 0.19 | 2, 5 | 1/A |
| 11 | 1 de Setembro | 11 | 0.09h00 | 0.1745D | B | 1/B |
| 12 | 1/12 | 2, 3 | 0,083 | 0.15 | 2, 3 | 1/C |
| 13 | 1/13 | 13 | 0.076923 | 0.13B | D | 1/D |
| 14 | 1/14 | 2, 7 | 0,0714285 | 0.1249 | 2, 7 | 1/E |
| 15 | 1/15 | 3, 5 | 0,06 | 0.1 | 3, 5 | 1/F |
| 16. | 1/16 | 2 | 0,0625 | 0.1 | 2 | 1/10 |
| 17. | 1/17 | 17. | 0.05882352941176 | 0.0F | 11 | 1 de Setembro |
| 18. | 1/18 | 2, 3 | 0,05 | 0,0E38 | 2, 3 | 1/12 |
| 19 | 1/19 | 19 | 0.0526315789368421 | 0.0D79435E5 | 13 | 1/13 |
| 20. | 1/20 | 2, 5 | 0,05 | 0,0C | 2, 5 | 1/14 |
| 21 | 1/21 | 3, 7 | 0.047619 | 0.0C3 | 3, 7 | 1/15 |
| 22 | 1/22 | 2, 11 | 0,045 | 0,0BA2E8 | 2, B | 1/16 |
| 23 | 1/23 | 23 | 0.0434782608695652173913 | 0.0B21642C859 | 17. | 1/17 |
| 24. | 1/24 | 2, 3 | 0,016 | 0,0A | 2, 3 | 1/18 |
| 25 | 1/25 | 5 | 0,04 | 0.0A3D7 | 5 | 1/19 |
| 26 | 1/26 | 2, 13 | 0,0384615 | 0,09D8 | 2, D | 1/1A |
| 27 | 1/27 | 3 | 0.037 | 0.097B425 | 3 | 1/1B |
| 28 | 1/28 | 2, 7 | 0,03571428 | 0,0924 | 2, 7 | 1/1C |
| 29 de Março | 1/29 | 29 de Março | 0.034482758668961724137931 | 0.08D3DCB | 1D | 1/1D |
| 30 | 1/30 | 2, 3, 5 | 0,03 | 0,08 | 2, 3, 5 | 1/1E |
| 31 | 1/31 | 31 | 0.032258064516129 | 0.08421 | 1F | 1/1F |
| 32 | 1/32 | 2 | 0,03125 | 0,08 | 2 | 1/20 |
| 33 | 1/33 | 3, 11 | 0.03:03 | 0.07C1F | 3, B | 1/21 |
| 34 | 1/34 | 2, 17. | 0,02941176470588235 | 0,078 | 2, 11 | 1/22 |
| 35 | 1/35 | 5, 7 | 0,0285714 | 0.075 | 5, 7 | 1/23 |
| 36 | 1/36 | 2, 3 | 0,027 | 0,071C | 2, 3 | 1/24 |
Números irracionais
A tabela abaixo fornece as expansões de alguns números irracionais comuns em decimal e hexadecimal.
| Número | Representação posicional | |
|---|---|---|
| Decimal | Hexadecimal | |
| √2 (o comprimento da diagonal de uma unidade quadrada) | 1.414213562373095048... | 1.6A09E667F3BCD... |
| √3 (o comprimento da diagonal de um cubo de unidade) | 1.732050807568877293... | 1.BB67AE8584CAA... |
| √5 (o comprimento da diagonal de um 1 × 2 retângulo) | 2.236067977499789696... | 2.3C6EF372FE95... |
| φ (phi, a proporção de ouro = (1+)√5)/2) | 1.618033988749894848... | 1.9E3779B97F4A... |
| D (pi, a proporção de circunferência ao diâmetro de um círculo) | 3.141592653589793238462643 383279502884197169399375105... | 3.243F6A8885A308D3198A2E0 3707344A4093822299F31D008... |
| e (a base do logaritmo natural) | 2.718281828459045235... | 2.B7E151628AED2A6B... |
| ? (a constante Thue-Morse) | 0454033640107597... | 0.6996 9669 9669 6996... |
| γ (a diferença limite entre a série harmônica e o logaritmo natural) | 0,577215664901532860... | 0.93C467E37DB0C7A4D1B... |
Poderes
As potências de dois têm expansões muito simples em hexadecimal. As primeiras dezesseis potências de dois são mostradas abaixo.
| 2x | Valor | Valor (decimal) |
|---|---|---|
| 20 | 1 | 1 |
| 21 | 2 | 2 |
| 22 | 4 | 4 |
| 23 | 8 | 8 |
| 24 | 10.Hex | 16.dec |
| 25 | 20.Hex | 32dec |
| 26 | 40Hex | 64dec |
| 27 | 80Hex | 128dec |
| 28 | 100.Hex | 256.dec |
| 29 | 200Hex | 512dec |
| 2A (210.dec) | 400Hex | 1024dec |
| 2B (211dec) | 800Hex | 2048dec |
| 2C (212dec) | 1000Hex | 4096dec |
| 2D (213dec) | 2000Hex | 8192dec |
| 2E (214dec) | 4000Hex | 16,384dec |
| 2F (215dec) | 8000Hex | 32,768dec |
| 210. (216.dec) | 10000Hex | 65,536dec |
História cultural
As unidades de medida chinesas tradicionais eram a base 16. Por exemplo, um jīn (斤) no sistema antigo é igual a dezesseis taéis. O suanpan (ábaco chinês) pode ser usado para realizar cálculos hexadecimais, como adições e subtrações.
Assim como no sistema duodecimal, houve tentativas ocasionais de promover o hexadecimal como o sistema numérico preferido. Essas tentativas geralmente propõem pronúncia e símbolos específicos para os numerais individuais. Algumas propostas unificam medidas padrão para que sejam múltiplos de 16. Uma das primeiras propostas desse tipo foi apresentada por John W. Nystrom em Project of a New System of Arithmetic, Weight, Measure and Coins: Proposed to be called the Tonal System, with Sixteen to the Base, publicado em 1862. Nystrom, entre outras coisas, sugeriu o tempo hexadecimal, que subdivide um dia em 16, para que haja 16 "horas" (ou "10 tims", pronuncia-se tontim) em um dia.
A palavra hexadecimal foi registrada pela primeira vez em 1952. É macarônica no sentido de que combina o grego ἕξ (hex) "seis" com -decimal latino. A alternativa totalmente latina sexadecimal (compare a palavra sexagesimal para a base 60) é mais antiga e é usada pelo menos ocasionalmente desde o final do século XIX. Ainda está em uso na década de 1950 na documentação do Bendix. Schwartzman (1994) argumenta que o uso de sexadecimal pode ter sido evitado por causa de sua abreviação sugestiva para sexo. Muitas línguas ocidentais desde a década de 1960 adotaram termos equivalentes em formação a hexadecimal (por exemplo, francês hexadécimal, italiano esadecimale, romeno hexazecimal i>, sérvio хексадецимални, etc.) mas outros introduziram termos que substituem palavras nativas por "dezesseis" (por exemplo, grego δεκαεξαδικός, islandês sextándakerfi, russo шестнадцатеричной etc.)
A terminologia e a notação não se estabeleceram até o final da década de 1960. Donald Knuth em 1969 argumentou que o termo etimologicamente correto seria senidenário, ou possivelmente sedenário, um termo latino destinado a transmitir "agrupado por 16" modelado em binário, ternário e quaternário etc. De acordo com o argumento de Knuth, os termos corretos para aritmética decimal e octal seriam denário e octonário, respectivamente. Alfred B. Taylor usou senidenário em seu trabalho de meados de 1800 sobre bases numéricas alternativas, embora tenha rejeitado a base 16 por causa de seu "número inconveniente de dígitos".
A notação atual usando as letras de A a F estabelece-se como o padrão de fato a partir de 1966, na sequência do publicação do manual Fortran IV para IBM System/360, que (ao contrário das variantes anteriores do Fortran) reconhece um padrão para inserir constantes hexadecimais. Conforme observado acima, notações alternativas foram usadas pela NEC (1960) e The Pacific Data Systems 1020 (1964). O padrão adotado pela IBM parece ter sido amplamente adotado em 1968, quando Bruce Alan Martin em sua carta ao editor do CACM reclama que
Com a escolha ridícula de letras A, B, C, D, E, F como símbolos de número hexadecimais adicionando a problemas já problemáticos de distinguir números octais (ou hex) de números decimais (ou nomes variáveis), o tempo é exagerado para reconsideração de nossos símbolos de número. Isso deve ter sido feito antes de escolhas pobres geladas em um padrão de fato!
O argumento de Martin era que o uso de numerais de 0 a 9 em números não decimais "implica para nós um esquema de valor posicional de base dez": "Por que não usar símbolos (e nomes) totalmente novos para os sete ou quinze dígitos diferentes de zero necessários em octal ou hexadecimal. Mesmo o uso das letras de A a P seria uma melhoria, mas símbolos inteiramente novos poderiam refletir a natureza binária do sistema". Ele também argumentou que "reutilizar letras alfabéticas para dígitos numéricos representa um retrocesso gigantesco em relação à invenção de glifos não alfabéticos distintos para numerais dezesseis séculos atrás" (como numerais Brahmi, e mais tarde em um sistema de numeração hindu-arábico), e que os recentes padrões ASCII (ASA X3.4-1963 e USAS X3.4-1968) "deveria ter preservado seis posições da tabela de códigos seguindo os dez dígitos decimais -- em vez de preenchê-los desnecessariamente com caracteres de pontuação" (":;<=>?") que pode ter sido colocado em outro lugar entre as 128 posições disponíveis.
Base16 (codificação de transferência)
Base16 (como um nome próprio sem espaço) também pode se referir a um binário para codificação de texto pertencente à mesma família que Base32, Base58 e Base64.
Nesse caso, os dados são divididos em sequências de 4 bits e cada valor (entre 0 e 15 inclusive) é codificado usando um dos 16 símbolos do conjunto de caracteres ASCII. Embora quaisquer 16 símbolos do conjunto de caracteres ASCII possam ser usados, na prática os dígitos ASCII '0'–'9' e as letras 'A'–'F' (ou as minúsculas 'a'–'f') são sempre escolhidas para alinhar com a notação escrita padrão para números hexadecimais.
Existem várias vantagens da codificação Base16:
- A maioria das linguagens de programação já tem instalações para analisar hexadecimal codificado ASCII
- Ser exatamente meio byte, 4 bits é mais fácil de processar do que os 5 ou 6 bits de Base32 e Base64 respectivamente
- Os símbolos 0-9 e A-F são universais na notação hexadecimal, por isso é facilmente compreendido de relance sem precisar confiar em uma tabela de pesquisa de símbolos
- Muitas arquiteturas de CPU têm instruções dedicadas que permitem o acesso a um meio-byte (também conhecido como "nibble"), tornando-o mais eficiente em hardware do que Base32 e Base64
As principais desvantagens da codificação Base16 são:
- A eficiência do espaço é apenas 50%, uma vez que cada valor de 4 bits dos dados originais será codificado como um byte de 8 bits. Em contraste, as codificações Base32 e Base64 têm uma eficiência espacial de 63% e 75% respectivamente.
- Possível complexidade adicional de ter de aceitar letras maiúsculas e minúsculas
Suporte para codificação Base16 é onipresente na computação moderna. É a base para o padrão W3C para codificação de porcentagem de URL, onde um caractere é substituído por um sinal de porcentagem "%" e sua forma codificada em Base16. A maioria das linguagens de programação modernas inclui suporte direto para formatação e análise de números codificados em Base16.
Contenido relacionado
Eliminação gaussiana
Teoria da complexidade computacional
Média aritmética-geométrica