Geometria algébrica

ImprimirCitar

Ramo da matemática

Esta superfície de Togliatti é uma superfície algébrica de grau cinco. A imagem representa uma parte do seu verdadeiro gafanhoto.

Geometria algébrica é um ramo da matemática que estuda classicamente zeros de polinômios multivariados. A geometria algébrica moderna é baseada no uso de técnicas algébricas abstratas, principalmente da álgebra comutativa, para resolver problemas geométricos sobre esses conjuntos de zeros.

Os objetos fundamentais de estudo da geometria algébrica são as variedades algébricas, que são manifestações geométricas de soluções de sistemas de equações polinomiais. Exemplos das classes mais estudadas de variedades algébricas são: curvas algébricas planas, que incluem linhas, círculos, parábolas, elipses, hipérboles, curvas cúbicas como curvas elípticas e curvas quárticas como lemniscatas e ovais de Cassini. Um ponto do plano pertence a uma curva algébrica se suas coordenadas satisfazem uma dada equação polinomial. Questões básicas envolvem o estudo dos pontos de interesse especial como os pontos singulares, os pontos de inflexão e os pontos no infinito. Questões mais avançadas envolvem a topologia da curva e as relações entre as curvas dadas por diferentes equações.

A geometria algébrica ocupa um lugar central na matemática moderna e tem múltiplas conexões conceituais com campos tão diversos como análise complexa, topologia e teoria dos números. Inicialmente um estudo de sistemas de equações polinomiais em diversas variáveis, a disciplina de geometria algébrica começa onde a resolução de equações termina, e torna-se ainda mais importante entender as propriedades intrínsecas da totalidade de soluções de um sistema de equações do que encontrar um solução; isso leva a algumas das áreas mais profundas de toda a matemática, tanto conceitualmente quanto em termos de técnica.

No século 20, a geometria algébrica se dividiu em várias subáreas.

O mainstream da geometria algébrica é dedicado ao estudo dos pontos complexos das variedades algébricas e, mais geralmente, aos pontos com coordenadas em um campo algébricamente fechado.
A geometria algébrica real é o estudo dos pontos reais de uma variedade algébrica.
Geometria diofantina e, mais geralmente, a geometria aritmética é o estudo dos pontos de uma variedade algébrica com coordenadas em campos que não estão algébricamente fechados e ocorrem na teoria dos números algébricas, como o campo de números racionais, campos numéricos, campos finitos, campos de função e campos p-ádicos.
Uma grande parte da teoria da singularidade é dedicada às singularidades das variedades algébricas.
A geometria algébrica computacional é uma área que surgiu na interseção da geometria algébrica e álgebra computacional, com o aumento dos computadores. Consiste principalmente em design de algoritmo e desenvolvimento de software para o estudo de propriedades de variedades algébricas explicitamente dadas.

Grande parte do desenvolvimento do mainstream da geometria algébrica no século 20 ocorreu dentro de uma estrutura algébrica abstrata, com ênfase crescente sendo colocada na geometria "intrínseca" propriedades de variedades algébricas não dependentes de qualquer forma particular de embutir a variedade em um espaço coordenado ambiente; isso acompanha os desenvolvimentos em topologia, diferencial e geometria complexa. Uma conquista importante dessa geometria algébrica abstrata é a teoria do esquema de Grothendieck, que permite usar a teoria dos feixes para estudar variedades algébricas de uma maneira muito semelhante ao seu uso no estudo de variedades diferenciais e analíticas. Isto é obtido estendendo a noção de ponto: Na geometria algébrica clássica, um ponto de uma variedade afim pode ser identificado, através do Nullstellensatz de Hilbert, com um ideal maximal do anel de coordenadas, enquanto os pontos do esquema afim correspondente são todos ideais primos deste anel. Isso significa que um ponto de tal esquema pode ser um ponto usual ou uma subvariedade. Essa abordagem também permite uma unificação da linguagem e das ferramentas da geometria algébrica clássica, principalmente preocupada com pontos complexos, e da teoria algébrica dos números. Wiles' A prova da conjectura de longa data chamada Último Teorema de Fermat é um exemplo do poder dessa abordagem.

Noções básicas

Zeros de polinômios simultâneos

Esfera e círculo inclinado

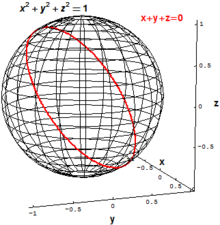
Na geometria algébrica clássica, os principais objetos de interesse são os conjuntos evanescentes de coleções de polinômios, ou seja, o conjunto de todos os pontos que satisfazem simultaneamente uma ou mais equações polinomiais. Por exemplo, a esfera bidimensional de raio 1 no espaço euclidiano tridimensional R³ pode ser definida como o conjunto de todos os pontos (x,y,z) com

x^{2}+y^{2}+z^{2}-1=0.,

Um "inclinado" círculo em R³ pode ser definido como o conjunto de todos os pontos (x,y,z ) que satisfazem as duas equações polinomiais

x^{2}+y^{2}+z^{2}-1=0,,

x+y+z=0.,

Variedades afins

Primeiro começamos com um campo k. Na geometria algébrica clássica, esse corpo sempre foi o número complexo C, mas muitos dos mesmos resultados são verdadeiros se assumirmos apenas que k é algebricamente fechado. Consideramos o espaço afim de dimensão n sobre k, denotado Aⁿ(k) (ou mais simplesmente Aⁿ, quando k está claro no contexto). Quando se fixa um sistema de coordenadas, pode-se identificar Aⁿ(k) com kⁿ. O propósito de não trabalhar com kⁿ é enfatizar que "esquece" a estrutura do espaço vetorial que kⁿ carrega.

Uma função f: Aⁿ → A¹ é dito ser polinomial (ou regular) se puder ser escrito como um polinômio, isto é, se houver um polinômio p em k[x₁,...,x_n] tal que f(M) = p(t₁,...,t_n) para cada ponto M com coordenadas (t ₁,...,t_n) em A ⁿ. A propriedade de uma função ser polinomial (ou regular) não depende da escolha de um sistema de coordenadas em Aⁿ.

Quando um sistema de coordenadas é escolhido, as funções regulares no espaço n afim podem ser identificadas com o anel de funções polinomiais em n variáveis sobre k . Portanto, o conjunto das funções regulares em Aⁿ é um anel, que é denotado k[Aⁿ].

Dizemos que um polinômio desaparece em um ponto se avaliá-lo nesse ponto dá zero. Seja S um conjunto de polinômios em k[Aⁿ]. O conjunto de fuga de S (ou lugar de fuga ou conjunto de zero) é o conjunto V(S ) de todos os pontos em Aⁿ onde todo polinômio em S desaparece. Simbolicamente,

{displaystyle V(S)={(t_{1},dotst_{n})mid p(t_{1},dotst_{n})=0{text{ for all }}pin S}.,}

Um subconjunto de Aⁿ que é V(S), para algum S, é chamado de conjunto algébrico. O V significa variedade (um tipo específico de conjunto algébrico a ser definido abaixo).

Dado um subconjunto U de Aⁿ, pode-se recuperar o conjunto de polinômios que o gerou? Se U for qualquer subconjunto de Aⁿ, defina I(U) para ser o conjunto de todos os polinômios cujo conjunto de fuga contém U. O I significa ideal: se dois polinômios f e g desaparecem em U, então f +g desaparece em U, e se h for qualquer polinômio, então hf desaparece em U, então I(U) é sempre um ideal do anel polinomial k[Aⁿ].

Duas perguntas naturais a serem feitas são:

Dado um subconjunto U de Aⁿ, quando é U = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = V(Eu...(U))?
Dado um conjunto S de polinômios, quando é S = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = Eu...(V(S))?

A resposta para a primeira pergunta é fornecida pela introdução da topologia Zariski, uma topologia em Aⁿ cujos conjuntos fechados são os conjuntos algébricos, e que reflete diretamente a estrutura algébrica de k[Aⁿ]. Então U = V(I(U)) se e somente se U é um conjunto algébrico ou equivalentemente um conjunto fechado de Zariski. A resposta para a segunda pergunta é dada por Nullstellensatz de Hilbert. Em uma de suas formas, diz que I(V(S)) é o radical do ideal gerado por S. Em linguagem mais abstrata, existe uma conexão de Galois, dando origem a dois operadores de fechamento; eles podem ser identificados e, naturalmente, desempenham um papel básico na teoria; o exemplo é elaborado na conexão Galois.

Por várias razões, nem sempre queremos trabalhar com o ideal inteiro correspondente a um conjunto algébrico U. O teorema da base de Hilbert implica que os ideais em k[Aⁿ] são sempre gerados finitamente.

Um conjunto algébrico é chamado irredutível se não puder ser escrito como a união de dois conjuntos algébricos menores. Qualquer conjunto algébrico é uma união finita de conjuntos algébricos irredutíveis e esta decomposição é única. Assim, seus elementos são chamados de componentes irredutíveis do conjunto algébrico. Um conjunto algébrico irredutível também é chamado de variedade. Acontece que um conjunto algébrico é uma variedade se e somente se pode ser definido como o conjunto nulo de um ideal primo do anel polinomial.

Alguns autores não fazem uma distinção clara entre conjuntos algébricos e variedades e usam variedade irredutível para fazer a distinção quando necessário.

Funções regulares

Assim como as funções contínuas são as aplicações naturais em espaços topológicos e as funções suaves são as aplicações naturais em variedades diferenciáveis, existe uma classe natural de funções em um conjunto algébrico, chamadas funções regulares ou funções polinomiais. Uma função regular em um conjunto algébrico V contido em Aⁿ é a restrição a V de uma função regular em Aⁿ. Para um conjunto algébrico definido no corpo dos números complexos, as funções regulares são suaves e até analíticas.

Pode parecer restritivo exigir que uma função regular sempre se estenda ao espaço ambiente, mas é muito semelhante à situação em um espaço topológico normal, onde o teorema da extensão de Tietze garante que uma função contínua em um subconjunto fechado sempre se estende ao espaço topológico ambiente.

Assim como as funções regulares no espaço afim, as funções regulares em V formam um anel, que denotamos por k[V ]. Este anel é chamado de anel coordenado de V.

Como funções regulares em V vêm de funções regulares em Aⁿ, há uma relação entre os anéis de coordenadas. Especificamente, se uma função regular em V é a restrição de duas funções f e g em k[Aⁿ], então f − g é uma função polinomial que é nula em V e, portanto, pertence a I(V). Assim, k[V] pode ser identificado com k[Aⁿ]/I(V).

Morfismo de variedades afins

Usando funções regulares de uma variedade afim para A¹, podemos definir mapas regulares de uma variedade afim para outra. Primeiro vamos definir um mapa regular de uma variedade para um espaço afim: Seja V uma variedade contida em Aⁿ. Escolha funções regulares m em V e chame-as de f₁,..., f_m. Definimos um mapa regular f de V a A^m deixando f = (f₁,..., f_m). Em outras palavras, cada f_i determina uma coordenada do intervalo de f.

Se V′ é uma variedade contida em A^m, dizemos que f é um mapa regular de V a V′ se o intervalo de f estiver contido em V′.

A definição das aplicações regulares também se aplica a conjuntos algébricos. Os mapas regulares também são chamados de morfismos, pois fazem a coleção de todos os conjuntos algébricos afins em uma categoria, onde os objetos são os conjuntos algébricos afins e os morfismos são os mapas regulares. As variedades afins são uma subcategoria da categoria dos conjuntos algébricos.

Dado um mapa regular g de V para V′ e uma função regular f de k[V′], então f ∘ g ∈ k[V]. O mapa f → f ∘ g é um homomorfismo de anéis de k[V′] para k[V]. Reciprocamente, todo homomorfismo de anel de k[V′] a k[V] define um mapa regular de V a V′. Isso define uma equivalência de categorias entre a categoria de conjuntos algébricos e a categoria oposta das k-álgebras reduzidas finitamente geradas. Essa equivalência é um dos pontos de partida da teoria dos esquemas.

Função racional e equivalência birracional

Em contraste com as seções anteriores, esta seção trata apenas de variedades e não de conjuntos algébricos. Por outro lado, as definições estendem-se naturalmente às variedades projetivas (próxima seção), pois uma variedade afim e sua complementação projetiva têm o mesmo campo de funções.

Se V é uma variedade afim, seu anel de coordenadas é um domínio inteiro e tem, portanto, um corpo de frações que é denotado k(V) e chamou o campo das funções racionais no V ou, resumidamente, o campo da função do V. Seus elementos são as restrições a V das funções racionais sobre o espaço afim contendo V. O domínio de uma função racional f não é V, mas o complemento da subvariedade (uma hipersuperfície) onde o denominador de f desaparece.

Tal como acontece com os mapas regulares, pode-se definir um mapa racional de uma variedade V a uma variedade V'. Como nos mapas regulares, os mapas racionais de V a V' podem ser identificados para os homomorfismos de campo de k(V') a k(V).

Duas variedades afins são birracionalmente equivalentes se existem duas funções racionais entre elas que são inversas uma à outra nas regiões onde ambas são definidas. Equivalentemente, eles são birracionalmente equivalentes se seus campos de função forem isomórficos.

Uma variedade affine é uma variedade racional se é biracionalmente equivalente a um espaço affine. Isso significa que a variedade admite um parâmetros racionais, que é uma parametrização com funções racionais. Por exemplo, o círculo da equação $x^{2}+y^{2}-1=0$ é uma curva racional, pois tem a equação paramétrica

x={frac {2,t}{1+t^{2}}}

y={frac {1-t^{2}}{1+t^{2}}},,

que também pode ser visto como um mapa racional da linha ao círculo.

O problema de resolução de singularidades é saber se toda variedade algébrica é birracionalmente equivalente a uma variedade cuja completude projetiva é não singular (ver também completude suave). Foi resolvido afirmativamente na característica 0 por Heisuke Hironaka em 1964 e ainda não foi resolvido na característica finita.

Variedade projetiva

Parabola (Sim. = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = x², vermelho) e cúbico (Sim. = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = x³, azul) em espaço projetivo

Assim como as fórmulas para as raízes dos polinômios de segundo, terceiro e quarto graus sugerem a extensão dos números reais para a configuração mais algebricamente completa dos números complexos, muitas propriedades das variedades algébricas sugerem a extensão do espaço afim para um espaço projetivo mais geometricamente completo. Considerando que os números complexos são obtidos pela adição do número i, uma raiz do polinômio x² + 1 , o espaço projetivo é obtido adicionando pontos apropriados "no infinito", pontos onde linhas paralelas podem se encontrar.

Para ver como isso pode acontecer, considere a variedade V(y − x²). Se desenharmos, obtemos uma parábola. À medida que x vai para o infinito positivo, a inclinação da linha desde a origem até o ponto (x, x²) também vai para o infinito positivo. Como x vai para infinito negativo, a inclinação da mesma linha vai para infinito negativo.

Compare isso com a variedade V(y − x³). Esta é uma curva cúbica. À medida que x vai para infinito positivo, a inclinação da linha desde a origem até o ponto (x, x³) vai para o infinito positivo como antes. Mas ao contrário de antes, como x vai para o infinito negativo, a inclinação da mesma linha vai para o infinito positivo também; exatamente o oposto da parábola. Portanto, o comportamento "no infinito" de V(y − x³) é diferente do comportamento "no infinito" de V(y − x²).

A consideração da completação projetiva das duas curvas, que é seu prolongamento "no infinito" no plano projetivo, permite quantificar essa diferença: o ponto no infinito da parábola é um ponto regular, cuja tangente é a reta no infinito, enquanto o ponto no infinito da curva cúbica é uma cúspide. Além disso, ambas as curvas são racionais, pois são parametrizadas por x, e o teorema de Riemann-Roch implica que a curva cúbica deve ter uma singularidade, que deve estar no infinito, como todos os seus pontos no afim espaço são regulares.

Assim, muitas das propriedades das variedades algébricas, incluindo a equivalência birracional e todas as propriedades topológicas, dependem do comportamento "no infinito" e assim é natural estudar as variedades no espaço projetivo. Além disso, a introdução de técnicas projetivas tornou muitos teoremas em geometria algébrica mais simples e nítidos: Por exemplo, o teorema de Bézout sobre o número de pontos de interseção entre duas variedades pode ser expresso em sua forma mais nítida apenas no espaço projetivo. Por essas razões, o espaço projetivo desempenha um papel fundamental na geometria algébrica.

Atualmente, o espaço projetivo Pⁿ de dimensão n costuma ser definido como o conjunto das retas que passam por um ponto, considerado como origem, no espaço afim de dimensão n + 1, ou equivalente ao conjunto das linhas vetoriais em um espaço vetorial de dimensão n + 1. Quando um sistema de coordenadas foi escolhido no espaço de dimensão n + 1, todos os pontos de uma linha têm o mesmo conjunto de coordenadas, até a multiplicação por um elemento de k. Isso define as coordenadas homogêneas de um ponto de Pⁿ como uma sequência de n + 1 elementos do campo base k, definido até a multiplicação por um elemento diferente de zero de k (o mesmo para toda a sequência).

Um polinômio em n + 1 variáveis desaparece em todos os pontos de uma linha que passa pela origem se e somente se for homogêneo. Neste caso, diz-se que o polinômio desaparece no ponto correspondente de Pⁿ. Isso nos permite definir um conjunto algébrico projetivo em Pⁿ como o conjunto V(f₁,..., f_k), onde um conjunto finito de polinômios homogêneos {f₁,..., f_k} desaparece. Como para os conjuntos algébricos afins, há uma bijeção entre os conjuntos algébricos projetivos e os ideais homogêneos reduzidos que os definem. As variedades projetivas são os conjuntos algébricos projetivos cujo ideal definidor é primo. Em outras palavras, uma variedade projetiva é um conjunto algébrico projetivo, cujo anel homogêneo de coordenadas é um domínio integral, o anel de coordenadas projetivas sendo definido como o quociente do anel graduado ou dos polinômios em n + 1 variáveis pelo ideal homogêneo (reduzido) que define a variedade. Todo conjunto algébrico projetivo pode ser decomposto de forma única em uma união finita de variedades projetivas.

As únicas funções regulares que podem ser definidas adequadamente em uma variedade projetiva são as funções constantes. Assim, esta noção não é usada em situações projetivas. Por outro lado, o campo das funções racionais ou campo da função é uma noção útil, que, similarmente ao caso afim, é definido como o conjunto dos quocientes de dois elementos homogêneos do mesmo grau no anel homogêneo de coordenadas.

Geometria algébrica real

A geometria algébrica real é o estudo dos pontos reais das variedades algébricas.

O fato de que o campo dos números reais é um campo ordenado não pode ser ignorado em tal estudo. Por exemplo, a curva da equação $x^{2}+y^{2}-a=0$ é um círculo se $0}" xmlns="http://www.w3.org/1998/Math/MathML">um>0- Sim. 0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1f34a80ea013edb56e340b19550430a8b6dfd7b9" style="vertical-align: -0.338ex; width:5.491ex; height:2.176ex;"/>$ , mas não tem nenhum ponto real se $<math alttext="{displaystyle aum<0Não. <img alt="a$ . Segue-se que a geometria algébrica real não é apenas o estudo das variedades algébricas reais, mas foi generalizada ao estudo da conjuntos semi-algebraicos, que são as soluções de sistemas de equações polinomiais e desigualdades polinomiais. Por exemplo, um ramo da hiperbola da equação $xy-1=0$ não é uma variedade algébrica, mas é um conjunto semi-algebraico definido por $xy-1=0$ e $0}" xmlns="http://www.w3.org/1998/Math/MathML">x>0- Sim. 0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/80d24be5f0eb4a9173da6038badc8659546021d0" style="vertical-align: -0.338ex; width:5.591ex; height:2.176ex;"/>$ ou por $xy-1=0$ e $0}" xmlns="http://www.w3.org/1998/Math/MathML">x+Sim.>0- Sim. 0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/715be5e4451f1cf6cd7b78a30b6dd7299f938f61" style="vertical-align: -0.671ex; width:9.586ex; height:2.509ex;"/>$ .

Um dos problemas desafiadores da geometria algébrica real é o décimo sexto problema não resolvido de Hilbert: decidir quais posições respectivas são possíveis para as ovais de uma curva plana não singular de grau 8.

Geometria algébrica computacional

Pode-se datar a origem da geometria algébrica computacional no encontro EUROSAM'79 (Simpósio Internacional de Manipulação Simbólica e Algébrica) realizado em Marselha, França, em junho de 1979. Nesse encontro,

Dennis S. Arnon mostrou que a decomposição algébrica cilíndrica de George E. Collins (CAD) permite a computação da topologia de conjuntos semi-algebraicos,
Bruno Buchberger apresentou as bases Gröbner e seu algoritmo para computá-los,
Daniel Lazard apresentou um novo algoritmo para resolver sistemas de equações polinomiais homogêneas com uma complexidade computacional que é essencialmente polinomial no número esperado de soluções e, portanto, simplesmente exponencial no número dos desconhecidos. Este algoritmo está fortemente relacionado com o resultado multivariado de Macaulay.

Desde então, a maioria dos resultados nesta área estão relacionados a um ou vários desses itens, seja usando ou melhorando um desses algoritmos, seja encontrando algoritmos cuja complexidade é simplesmente exponencial no número de variáveis.

Um corpo de teoria matemática complementar aos métodos simbólicos chamado geometria algébrica numérica foi desenvolvido nas últimas décadas. O principal método computacional é a continuação de homotopia. Isso suporta, por exemplo, um modelo de computação de ponto flutuante para resolver problemas de geometria algébrica.

Base de Gröbner

Uma base de Gröbner é um sistema de geradores de um ideal polinomial cujo cálculo permite a dedução de muitas propriedades da variedade algébrica afim definida pelo ideal.

Dado um I ideal definindo um conjunto algébrico V:

V é vazio (sobre uma extensão algébrica fechada do campo de base), se e somente se a base de Gröbner para qualquer ordenação monomial é reduzida a {1}.
Por meio da série Hilbert pode-se calcular a dimensão e o grau de V de qualquer base de Gröbner Eu... para uma ordenação monomial refinando o grau total.
Se a dimensão de V é 0, pode-se calcular os pontos (finito em número) de V de qualquer base de Gröbner Eu... (ver Sistemas de equações polinomiais).
Uma computação de base Gröbner permite que se remova de V todos os componentes irredutíveis que estão contidos em uma determinada hipersuperfície.
Uma computação de base de Gröbner permite calcular o fechamento de Zariski da imagem de V pela projeção na k primeiro coordena, e o subconjunto da imagem onde a projeção não é adequada.
Mais geralmente Gröbner base computações permitem que se compute o fechamento Zariski da imagem e os pontos críticos de uma função racional de V em outra variedade affine.

Os cálculos de base de Gröbner não permitem calcular diretamente a decomposição primária de I nem os ideais primos que definem os componentes irredutíveis de V, mas a maioria dos algoritmos para isso envolve Gröbner cálculo de base. Os algoritmos que não são baseados em bases de Gröbner usam cadeias regulares, mas podem precisar de bases de Gröbner em algumas situações excepcionais.

As bases de Gröbner são consideradas difíceis de calcular. Na verdade, eles podem conter, no pior caso, polinômios cujo grau é duplamente exponencial no número de variáveis e um número de polinômios também duplamente exponencial. No entanto, esta é apenas uma complexidade de pior caso, e o limite de complexidade do algoritmo de Lazard de 1979 pode ser aplicado com frequência. O algoritmo Faugère F5 percebe essa complexidade, pois pode ser visto como uma melhoria do algoritmo de Lazard de 1979. Segue-se que as melhores implementações permitem calcular quase rotineiramente com conjuntos algébricos de grau superior a 100. Isso significa que, atualmente, a dificuldade de calcular uma base de Gröbner está fortemente relacionada à dificuldade intrínseca do problema.

Decomposição algébrica cilíndrica (CAD)

CAD é um algoritmo que foi introduzido em 1973 por G. Collins para implementar com uma complexidade aceitável o teorema de Tarski–Seidenberg sobre a eliminação de quantificadores sobre os números reais.

Este teorema diz respeito às fórmulas da lógica de primeira ordem cujas fórmulas atômicas são igualdades polinomiais ou desigualdades entre polinômios com coeficientes reais. Essas fórmulas são, portanto, as fórmulas que podem ser construídas a partir das fórmulas atômicas pelos operadores lógicos e (∧), ou (∨), não (¬), para todos (∀) e existe (∃). O teorema de Tarski afirma que, a partir de tal fórmula, pode-se calcular uma fórmula equivalente sem quantificador (∀, ∃).

A complexidade do CAD é duplamente exponencial no número de variáveis. Isso significa que o CAD permite, em teoria, resolver todos os problemas de geometria algébrica real que podem ser expressos por tal fórmula, ou seja, quase todos os problemas relativos a variedades explicitamente dadas e conjuntos semi-algébricos.

Enquanto a computação básica de Gröbner tem complexidade duplamente exponencial apenas em casos raros, o CAD tem quase sempre essa alta complexidade. Isso implica que, a menos que a maioria dos polinômios que aparecem na entrada sejam lineares, pode não resolver problemas com mais de quatro variáveis.

Desde 1973, a maior parte da pesquisa sobre este assunto é dedicada a melhorar o CAD ou encontrar algoritmos alternativos em casos especiais de interesse geral.

Como exemplo do estado da arte, existem algoritmos eficientes para encontrar pelo menos um ponto em cada componente conectada de um conjunto semialgébrico e, assim, testar se um conjunto semialgébrico está vazio. Por outro lado, o CAD ainda é, na prática, o melhor algoritmo para contar o número de componentes conectados.

Complexidade assintótica vs. eficiência prática

Os algoritmos gerais básicos da geometria computacional têm uma dupla complexidade exponencial pior caso. Mais precisamente, se D é o grau máximo dos polinômios de entrada e n o número de variáveis, sua complexidade é no máximo $d^{2^{cn}}$ para alguma constante c, e, para algumas entradas, a complexidade é pelo menos $d^{2^{c'n}}$ para outra constante c′.

Durante os últimos 20 anos do século XX, vários algoritmos foram introduzidos para resolver subproblemas específicos com uma melhor complexidade. A maioria desses algoritmos tem uma complexidade $d^{O(n^{2})}$ .

Entre esses algoritmos que resolvem um subproblema dos problemas resolvidos por bases de Gröbner, pode-se citar teste se uma variedade afim está vazia e solução de sistemas polinomiais não homogêneos que possuem um número finito de soluções. Esses algoritmos raramente são implementados porque, na maioria das entradas, os algoritmos F4 e F5 de Faugère têm uma melhor eficiência prática e provavelmente uma complexidade semelhante ou melhor (provavelmente porque a avaliação de a complexidade dos algoritmos de base de Gröbner em uma classe particular de entradas é uma tarefa difícil que foi realizada apenas em alguns casos especiais).

Os principais algoritmos da geometria algébrica real que resolvem um problema resolvido por CAD estão relacionados à topologia de conjuntos semi-algebraicos. Um pode citar contando o número de componentes conectados, testar se dois pontos estão nos mesmos componentes ou computando uma estratificação Whitney de um conjunto algébrica real. Eles têm uma complexidade $d^{O(n^{2})}$ , mas a constante envolvida por O notação é tão alta que usá-los para resolver qualquer problema não trivial efetivamente resolvido por CAD, é impossível, mesmo que se possa usar todo o poder de computação existente no mundo. Portanto, esses algoritmos nunca foram implementados e esta é uma área de pesquisa ativa para procurar algoritmos com ter juntos uma boa complexidade assintótica e uma boa eficiência prática.

Ponto de vista moderno abstrato

As abordagens modernas da geometria algébrica redefinem e efetivamente estendem a gama de objetos básicos em vários níveis de generalidade para esquemas, esquemas formais, esquemas ind, espaços algébricos, pilhas algébricas e assim por diante. A necessidade disso já surge das idéias úteis dentro da teoria das variedades, por ex. as funções formais de Zariski podem ser acomodadas pela introdução de elementos nilpotentes em anéis de estrutura; considerar espaços de loops e arcos, construir quocientes por ações de grupo e desenvolver fundamentos formais para a teoria da interseção natural e a teoria da deformação levam a algumas das extensões adicionais.

O mais notável é que, no final da década de 1950, as variedades algébricas foram incluídas no conceito de esquema de Alexander Grothendieck. Seus objetos locais são esquemas afins ou espectros primos que são espaços com anéis localmente que formam uma categoria que é antiequivalente à categoria de anéis unitários comutativos, estendendo a dualidade entre a categoria de variedades algébricas afins sobre um corpo k, e a categoria de k-álgebras reduzidas finitamente geradas. A colagem é ao longo da topologia Zariski; pode-se colar dentro da categoria de espaços localmente anelados, mas também, usando a incorporação de Yoneda, dentro da categoria mais abstrata de pré-feixes de conjuntos sobre a categoria de esquemas afins. A topologia Zariski no sentido teórico conjunto é então substituída por uma topologia Grothendieck. Grothendieck introduziu as topologias Grothendieck tendo em mente exemplos mais exóticos, mas geometricamente mais refinados e mais sensíveis do que a topologia bruta de Zariski, ou seja, a topologia étale, e as duas topologias planas de Grothendieck: fppf e fpqc; hoje em dia, alguns outros exemplos se tornaram proeminentes, incluindo a topologia de Nisnevich. Feixes podem ser generalizados para pilhas no sentido de Grothendieck, geralmente com algumas condições de representabilidade adicionais levando a pilhas Artin e, ainda mais finas, pilhas Deligne-Mumford, ambas frequentemente chamadas de pilhas algébricas.

Às vezes, outros sites algébricos substituem a categoria de esquemas afins. Por exemplo, Nikolai Durov introduziu mônadas algébricas comutativas como uma generalização de objetos locais em uma geometria algébrica generalizada. Versões de uma geometria tropical, de uma geometria absoluta sobre um campo de um elemento e um análogo algébrico da geometria de Arakelov foram realizados nesta configuração.

Outra generalização formal é possível para a geometria algébrica universal na qual cada variedade de álgebras tem sua própria geometria algébrica. O termo variedade de álgebras não deve ser confundido com variedade algébrica.

A linguagem de esquemas, pilhas e generalizações provou ser uma forma valiosa de lidar com conceitos geométricos e tornou-se a pedra angular da geometria algébrica moderna.

Pilhas algébricas podem ser mais generalizadas e, para muitas questões práticas, como teoria da deformação e teoria da interseção, essa costuma ser a abordagem mais natural. Pode-se estender o sítio Grothendieck de esquemas afins para um sítio categórico superior de esquemas afins derivados, substituindo os anéis comutativos por uma categoria infinita de álgebras comutativas graduadas diferenciais, ou de anéis comutativos simpliciais ou uma categoria similar com uma variante apropriada de um Grothendieck topologia. Pode-se também substituir pré-feixes de conjuntos por pré-feixes de conjuntos simpliciais (ou de grupóides infinitos). Então, na presença de um maquinário homotópico apropriado, pode-se desenvolver uma noção de pilha derivada como tal pré-feixe na categoria infinita de esquemas afins derivados, que satisfaz certa versão categórica infinita de um axioma de feixe (e para ser algébrico, indutivamente uma sequência das condições de representabilidade). As categorias de modelos de Quillen, as categorias de Segal e as quasicategorias são algumas das ferramentas mais usadas para formalizar essa produção da geometria algébrica derivada, introduzida pela escola de Carlos Simpson, incluindo Andre Hirschowitz, Bertrand Toën, Gabrielle Vezzosi, Michel Vaquié e outros; e desenvolvido por Jacob Lurie, Bertrand Toën e Gabriele Vezzosi. Outra versão (não comutativa) da geometria algébrica derivada, usando categorias A-infinito, foi desenvolvida no início dos anos 1990 por Maxim Kontsevich e seguidores.

História

Antes do século XVI

Algumas das raízes da geometria algébrica remontam ao trabalho dos gregos helenísticos do século V aC. O problema Delian, por exemplo, era construir um comprimento x de forma que o cubo de lado x contivesse o mesmo volume que a caixa retangular a ²b para os lados dados a e b. Menaechmus (c. 350 AC) considerou o problema geometricamente cruzando o par de cônicas planas ay = x² e xy = ab. No século III aC, Arquimedes e Apolônio estudaram sistematicamente problemas adicionais em seções cônicas usando coordenadas. Apolônio nas Cônicas desenvolveu ainda mais um método que é tão semelhante à geometria analítica que às vezes se pensa que seu trabalho antecipou o trabalho de Descartes em cerca de 1800 anos. Sua aplicação de linhas de referência, um diâmetro e uma tangente não é essencialmente diferente da nossa uso moderno de um referencial de coordenadas, onde as distâncias medidas ao longo do diâmetro a partir do ponto de tangência são as abcissas, e os segmentos paralelos à tangente e interceptados entre o eixo e a curva são as ordenadas. Ele desenvolveu relações entre as abcissas e as coordenadas correspondentes usando métodos geométricos como o uso de parábolas e curvas. Matemáticos medievais, incluindo Omar Khayyam, Leonardo de Pisa, Gersonides e Nicole Oresme no período medieval resolveram certas equações cúbicas e quadráticas por meios puramente algébricos e então interpretaram os resultados geometricamente. O matemático persa Omar Khayyám (nascido em 1048 DC) acreditava que havia uma relação entre aritmética, álgebra e geometria. Isso foi criticado por Jeffrey Oaks, que afirma que o estudo das curvas por meio de equações se originou com Descartes no século XVII.

Renascimento

Essas técnicas de aplicação de construções geométricas a problemas algébricos também foram adotadas por vários matemáticos renascentistas, como Gerolamo Cardano e Niccolò Fontana "Tartaglia" em seus estudos da equação cúbica. A abordagem geométrica para problemas de construção, em vez da algébrica, foi favorecida pela maioria dos matemáticos dos séculos XVI e XVII, notadamente Blaise Pascal, que argumentou contra o uso de métodos algébricos e analíticos na geometria. Os matemáticos franceses Franciscus Vieta e mais tarde René Descartes e Pierre de Fermat revolucionaram a maneira convencional de pensar sobre problemas de construção através da introdução da geometria de coordenadas. Eles estavam interessados principalmente nas propriedades das curvas algébricas, como as definidas pelas equações diofantinas (no caso de Fermat), e na reformulação algébrica dos trabalhos gregos clássicos sobre cônicas e cúbicas (no caso de Descartes).

Durante o mesmo período, Blaise Pascal e Gérard Desargues abordaram a geometria de uma perspectiva diferente, desenvolvendo as noções sintéticas da geometria projetiva. Pascal e Desargues também estudaram curvas, mas do ponto de vista puramente geométrico: o análogo da construção grega régua e compasso. Em última análise, a geometria analítica de Descartes e Fermat venceu, pois forneceu aos matemáticos do século XVIII ferramentas quantitativas concretas necessárias para estudar problemas físicos usando o novo cálculo de Newton e Leibniz. No entanto, no final do século 18, a maior parte do caráter algébrico da geometria coordenada foi incluída no cálculo de infinitesimais de Lagrange e Euler.

Século XIX e início do século XX

Foram necessários os desenvolvimentos simultâneos da geometria não-euclidiana e das integrais abelianas no século XIX para trazer as velhas ideias algébricas de volta à dobra geométrica. O primeiro desses novos desenvolvimentos foi apreendido por Edmond Laguerre e Arthur Cayley, que tentaram determinar as propriedades métricas generalizadas do espaço projetivo. Cayley introduziu a ideia de formas polinomiais homogêneas, e mais especificamente formas quadráticas, no espaço projetivo. Posteriormente, Felix Klein estudou a geometria projetiva (juntamente com outros tipos de geometria) do ponto de vista de que a geometria em um espaço é codificada em uma certa classe de transformações no espaço. No final do século XIX, os geômetras projetivos estudavam tipos mais gerais de transformações em figuras no espaço projetivo. Ao invés das transformações lineares projetivas que eram normalmente consideradas como dando a geometria kleiniana fundamental no espaço projetivo, eles se preocuparam também com as transformações birracionais de grau mais alto. Essa noção mais fraca de congruência levaria mais tarde os membros da escola italiana de geometria algébrica do século XX a classificar as superfícies algébricas até o isomorfismo birracional.

O segundo desenvolvimento do início do século XIX, o das integrais abelianas, levaria Bernhard Riemann ao desenvolvimento das superfícies de Riemann.

Na mesma época começou a algebrização da geometria algébrica através da álgebra comutativa. Os resultados proeminentes nessa direção são o teorema da base de Hilbert e o Nullstellensatz de Hilbert, que são a base da conexão entre geometria algébrica e álgebra comutativa, e a resultante multivariada de Macaulay, que é a base da teoria da eliminação. Provavelmente por causa do tamanho da computação que é implicada por resultantes multivariados, a teoria da eliminação foi esquecida durante meados do século 20 até ser renovada pela teoria da singularidade e geometria algébrica computacional.

Século 20

B. L. van der Waerden, Oscar Zariski e André Weil desenvolveram uma base para a geometria algébrica baseada na álgebra comutativa contemporânea, incluindo a teoria da valoração e a teoria dos ideais. Um dos objetivos era fornecer uma estrutura rigorosa para provar os resultados da escola italiana de geometria algébrica. Em particular, essa escola utilizou sistematicamente a noção de ponto genérico sem definição precisa, que foi dada pela primeira vez por esses autores na década de 1930.

Nas décadas de 1950 e 1960, Jean-Pierre Serre e Alexander Grothendieck reformularam os fundamentos fazendo uso da teoria dos feixes. Mais tarde, por volta de 1960, e em grande parte liderado por Grothendieck, a ideia de esquemas foi elaborada, em conjunto com um aparato muito refinado de técnicas homológicas. Após uma década de rápido desenvolvimento, o campo se estabilizou na década de 1970, e novas aplicações foram feitas, tanto para a teoria dos números quanto para questões geométricas mais clássicas sobre variedades algébricas, singularidades, módulos e módulos formais.

Uma importante classe de variedades, não facilmente compreendida diretamente de suas equações definidoras, são as variedades abelianas, que são as variedades projetivas cujos pontos formam um grupo abeliano. Os exemplos prototípicos são as curvas elípticas, que possuem uma teoria rica. Eles foram fundamentais na prova do Último Teorema de Fermat e também são usados na criptografia de curvas elípticas.

Paralelamente à tendência abstrata da geometria algébrica, que se preocupa com afirmações gerais sobre variedades, também foram desenvolvidos métodos para computação efetiva com variedades concretamente dadas, que levam à nova área da geometria algébrica computacional. Um dos métodos fundadores desta área é a teoria das bases de Gröbner, introduzida por Bruno Buchberger em 1965. Outro método fundador, mais especialmente dedicado à geometria algébrica real, é a decomposição algébrica cilíndrica, introduzida por George E. Collins em 1973.

Veja também: geometria algébrica derivada.

Geometria analítica

Uma variedade analítica é definida localmente como o conjunto de soluções comuns de várias equações envolvendo funções analíticas. É análogo ao conceito incluído de variedade algébrica real ou complexa. Qualquer variedade complexa é uma variedade analítica. Como as variedades analíticas podem ter pontos singulares, nem todas as variedades analíticas são variedades.

A geometria analítica moderna é essencialmente equivalente à geometria algébrica real e complexa, como foi demonstrado por Jean-Pierre Serre em seu artigo GAGA, cujo nome é francês para geometria algébrica e geometria analítica. No entanto, os dois campos permanecem distintos, pois os métodos de prova são bastante diferentes e a geometria algébrica inclui também a geometria em característica finita.

Aplicativos

A geometria algébrica agora encontra aplicações em estatística, teoria de controle, robótica, códigos de correção de erros, filogenética e modelagem geométrica. Há também conexões com a teoria das cordas, teoria dos jogos, correspondências de grafos, sólitons e programação inteira.

Contenido relacionado

Más resultados...