Geodésia
Geodésia é a ciência de medir e representar a geometria, gravidade e orientação espacial da Terra em 3D com variação temporal. É chamado de geodésia planetária quando se estuda outros corpos astronômicos, como planetas ou sistemas circumplanetários.
Fenômenos geodinâmicos, incluindo movimento da crosta, marés e movimento polar, podem ser estudados projetando redes de controle globais e nacionais, aplicando geodésia espacial e técnicas geodésicas terrestres e contando com datums e sistemas de coordenadas. Os cargos são geodesista e agrimensor geodésico.
História
A geodésia começou na antiguidade pré-científica, então a própria palavra geodésia vem da palavra grega antiga γεωδαισία ou geodaisia (literalmente, "divisão da Terra").
Idéias iniciais sobre a figura da Terra sustentavam que a Terra era plana e os céus uma cúpula física que se estendia sobre ela. Dois argumentos iniciais para uma Terra esférica foram que os eclipses lunares aparecem para um observador como sombras circulares e que Polaris aparece cada vez mais baixo no céu para um viajante que se dirige para o sul.
Definição
No mundo de língua inglesa, a geodésia refere-se à ciência de medir e representar informações geoespaciais, enquanto a geomática abrange aplicações práticas da geodésia em escalas locais e regionais, incluindo levantamentos.
A geodésia no mundo de língua alemã consiste em geodésia superior (höhere Geodäsie ou Erdmessung, literalmente "geomensuração") — preocupado com a medição da Terra em escala global e geodésia prática ou geodésia de engenharia (Ingenieurgeodäsie) que inclui levantamento - medição de partes ou regiões da Terra.
Por muito tempo, a geodésia foi a ciência de medir e compreender a forma geométrica da Terra, a orientação no espaço e o campo gravitacional; no entanto, a ciência e as operações geodésicas também são aplicadas a outros corpos astronômicos em nosso Sistema Solar.
A forma da Terra é, em grande medida, resultado da rotação, que causa o seu bojo equatorial, e da competição de processos geológicos como a colisão de placas, bem como do vulcanismo, resistido pela Terra;s campo gravitacional. Isso se aplica à superfície sólida, à superfície líquida (topografia dinâmica da superfície do mar) e à atmosfera da Terra. Por esta razão, o estudo do campo gravitacional da Terra é chamado de geodésia física.
Geóide e elipsóide de referência
O geóide é essencialmente a figura da Terra abstraída de suas características topográficas. É uma superfície de equilíbrio idealizada da água do mar, a superfície média do nível do mar na ausência de correntes e variações de pressão do ar, e continua sob as massas continentais. Ao contrário de um elipsóide de referência, o geóide é irregular e muito complicado para servir como superfície computacional para resolver problemas geométricos como posicionamento de pontos. A separação geométrica entre o geóide e um elipsóide de referência é chamada de ondulação geoidal, e varia globalmente entre ±110 m com base no elipsóide GRS 80.
Um elipsóide de referência, normalmente escolhido para ter o mesmo tamanho (volume) do geóide, é descrito por seu semi-eixo maior (raio equatorial) a e achatamento f. A quantidade f = a − b /a, onde b é o semi-eixo menor (raio polar), é puramente geométrico. A elipticidade mecânica da Terra (achatamento dinâmico, símbolo J2) pode ser determinada com alta precisão pela observação das perturbações da órbita do satélite. Sua relação com o achatamento geométrico é indireta e depende da distribuição de densidade interna ou, em termos mais simples, do grau de concentração central de massa.
O Sistema de Referência Geodésica de 1980 (GRS 80), adotado na XVII Assembleia Geral da União Internacional de Geodésia e Geofísica (IUGG), postulou um semi-eixo maior de 6.378.137 m e um achatamento de 1:298.257. O GRS 80 constitui essencialmente a base para o posicionamento geodésico pelo Sistema de Posicionamento Global (GPS) e, portanto, também é amplamente utilizado fora da comunidade geodésica. Numerosos sistemas usados para mapeamento e gráficos estão se tornando obsoletos à medida que os países se movem cada vez mais para sistemas de referência geocêntricos globais, utilizando o elipsóide de referência GRS 80.
O geóide é uma área "realizável" superfície, o que significa que pode ser consistentemente localizado na Terra por medições simples adequadas de objetos físicos como um medidor de maré. O geóide pode, portanto, ser considerado uma superfície física ("real"). O elipsóide de referência, no entanto, tem muitas instanciações possíveis e não é prontamente realizável, por isso é uma superfície abstrata. A terceira superfície primária de interesse geodésico – a superfície topográfica da Terra – também é realizável.
Sistemas de coordenadas no espaço
As localizações dos pontos no espaço 3D são descritas de forma mais conveniente por três coordenadas cartesianas ou retangulares, X, Y e Z. Desde o advento do posicionamento por satélite, tais sistemas de coordenadas são tipicamente geocêntricos, com o eixo Z alinhado ao eixo de rotação da Terra (convencional ou instantâneo).
Antes da era da geodésia por satélite, os sistemas de coordenadas associados a um datum geodésico tentavam ser geocêntricos, mas com a origem diferindo do geocentro por centenas de metros devido a desvios regionais na direção do prumo (vertical). Esses datums geodésicos regionais, como ED 50 (datum europeu de 1950) ou NAD 27 (datum norte-americano de 1927), têm elipsoides associados a eles que são "melhores ajustes" aos geóides dentro de suas áreas de validade, minimizando os desvios da vertical sobre essas áreas.
É apenas porque os satélites GPS orbitam em torno do geocentro que este ponto se torna naturalmente a origem de um sistema de coordenadas definido por meios geodésicos de satélite, pois as próprias posições dos satélites no espaço são computadas dentro de tal sistema.
Sistemas de coordenadas geocêntricas usados em geodésia podem ser divididos naturalmente em duas classes:
- Os sistemas de referência inercial, onde os eixos de coordenadas mantêm sua orientação em relação às estrelas fixas ou, equivalentemente, aos eixos de rotação dos giroscópios ideais; X-axis aponta para o equinócio vernal
- Os sistemas de referência co-rotantes (também ECEF ou "Earth Centred, Earth Fixed"), em que os eixos são "anexados" ao corpo sólido da Terra. O X-axis está dentro do avião meridiano do observatório de Greenwich.
A transformação de coordenadas entre esses dois sistemas para uma boa aproximação é descrita pelo tempo sideral (aparente), que explica as variações na rotação axial da Terra (variações na duração do dia). Uma descrição mais precisa também considera o movimento polar como um fenômeno monitorado de perto pelos geodesistas.
Sistemas de coordenadas no plano
Em aplicações geodésicas como topografia e mapeamento, dois tipos gerais de sistemas de coordenadas no plano são usados:
- Plano-polar, com pontos no plano definidos pela sua distância, S, de um ponto especificado ao longo de um raio tendo uma direção α de uma linha de base ou eixo;
- Retangular, com pontos definidos por distâncias de dois eixos mutuamente perpendiculares, x e Sim.. Contrariamente à convenção matemática, na prática geodésica, x- pontos de eixo Norte e o Norte Sim.- Oaxis East.
Pode-se usar intuitivamente coordenadas retangulares no plano para a localização atual, caso em que o eixo x apontará para o norte local. Mais formalmente, tais coordenadas podem ser obtidas a partir de coordenadas 3D usando o artifício de uma projeção cartográfica. É impossível mapear a superfície curva da Terra em uma superfície de mapa plana sem deformação. O compromisso mais frequentemente escolhido - chamado de projeção conforme - preserva ângulos e proporções de comprimento para que pequenos círculos sejam mapeados como pequenos círculos e pequenos quadrados como quadrados.
Um exemplo de tal projeção é UTM (Universal Transverse Mercator). Dentro do plano do mapa, temos as coordenadas retangulares x e y. Neste caso, a direção norte usada como referência é o norte mapa, não o norte local. A diferença entre os dois é chamada de convergência meridiana.
É fácil "traduzir" entre coordenadas polares e retangulares no plano: deixe, como acima, direção e distância ser α e s respectivamente, então temos
- x= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Se α α Sim.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Specado α α {displaystyle {begin{aligned}x&=scos alpha \y&=ssin alpha end{aligned}}}
A transformação inversa é dada por:
- S= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =x2+Sim.2α α = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =arctan Sim.x.- Sim. {x^{2}+y^{2}}}\alpha &=arctan {frac {y}{x}}.end{aligned}}}
Alturas
Na geodésia, as alturas de pontos ou terrenos estão "acima do nível do mar" como uma superfície irregular e fisicamente definida. Os sistemas de altura em uso são:
- Alturas ortométricas
- Alturas dinâmicas
- Alturas geopotenciais
- Alturas normais
Cada sistema tem suas vantagens e desvantagens. As alturas ortométrica e normal são expressas em metros acima do nível do mar, enquanto os números geopotenciais são medidas de energia potencial (unidade: m2 s−2) e não métricas. A superfície de referência é o geóide, uma superfície equigeopotencial que se aproxima do nível médio do mar conforme descrito acima. Para alturas normais, a superfície de referência é o chamado quase-geóide, que tem alguns metros de separação do geóide devido à densidade assumida em sua continuação sob as massas continentais.
Pode-se relacionar essas alturas através do conceito de ondulação geoidal com alturas elipsoidais (também conhecidas como alturas geodésicas), representando a altura de um ponto acima do elipsóide de referência. Os receptores de posicionamento por satélite normalmente fornecem alturas elipsoidais, a menos que sejam equipados com um software de conversão especial baseado em um modelo do geóide.
Dados geodésicos
Como as coordenadas e alturas dos pontos geodésicos sempre são obtidas dentro de um sistema que foi construído com base em observações do mundo real, os geodesistas introduziram o conceito de "datum geodésico" (plural datums): uma realização física (do mundo real) de um sistema de coordenadas usado para descrever localizações de pontos. Esta realização decorre da escolha (portanto convencional) dos valores das coordenadas para um ou mais pontos de referência. No caso de dados de altura, basta escolher um ponto de referência — o referencial de referência, normalmente um medidor de maré na costa. Assim, temos datums verticais, como o NAVD 88 (North American Vertical Datum 1988), NAP (Normaal Amsterdams Peil), o datum de Kronstadt, o datum de Trieste e muitos outros.
Tanto na matemática quanto na geodésia, um sistema de coordenadas é um "sistema de coordenadas" por terminologia ISO, enquanto o Serviço Internacional de Rotação da Terra e Sistemas de Referência (IERS) usa o termo "sistema de referência" para o mesmo. Quando as coordenadas são realizadas escolhendo pontos de referência e fixando um datum geodésico, o ISO fala de um "sistema de referência de coordenadas", enquanto o IERS usa um "quadro de referência" para o mesmo. O termo ISO para uma transformação de dados novamente é uma "transformação de coordenadas".
Posicionamento
Geoposicionamento, ou simplesmente posicionamento, é a determinação da localização, definida por um conjunto de coordenadas geodésicas, de um ponto em terra, no mar ou no espaço dentro de um sistema de coordenadas (posicionamento de ponto) ou relativo a outro ponto (posicionamento relativo). Calcula-se a posição de um ponto no espaço a partir de medições que ligam pontos terrestres ou extraterrestres de localização conhecida ("pontos conhecidos") com pontos terrestres de localização desconhecida ("pontos desconhecidos"). A computação pode envolver transformações entre ou entre sistemas de coordenadas astronômicos e terrestres. Os pontos conhecidos usados no posicionamento de pontos podem ser satélites GNSS ou pontos de triangulação de uma rede de ordem superior.
Tradicionalmente, os geodesistas construíam uma hierarquia de redes para permitir o posicionamento de pontos dentro de um país. O mais alto nessa hierarquia eram as redes de triangulação, densificadas nas redes de travessias (polígonos) nas quais o mapeamento local e as medições de levantamento, geralmente coletadas usando uma fita métrica, um prisma de canto e os pólos vermelho e branco, são amarrados.
O GPS é comumente usado hoje em dia, exceto para medições especializadas (por exemplo, em engenharia subterrânea ou de alta precisão). As redes de ordem superior são medidas com GPS estático, usando medição diferencial para determinar vetores entre pontos terrestres. Esses vetores então são ajustados de uma forma tradicional de rede. Um poliedro global de estações GPS operando permanentemente sob os auspícios do IERS é a base para a definição de um único quadro de referência geocêntrico global que serve como a estrutura de "ordem zero" referência (global) à qual as medidas nacionais são anexadas.
O posicionamento cinemático em tempo real (RTK GPS) é empregado frequentemente no mapeamento de pesquisa. Nessa técnica de medição, pontos desconhecidos podem ser rapidamente vinculados a pontos conhecidos terrestres próximos.
Uma finalidade do posicionamento de ponto é o fornecimento de pontos conhecidos para medições de mapeamento, também conhecido como controle (horizontal e vertical). Pode haver milhares desses pontos determinados geodeticamente em um país, geralmente documentados por agências nacionais de mapeamento. Os agrimensores envolvidos em imóveis e seguros os usarão para vincular suas medições locais.
Problemas geodésicos
Na geodésia geométrica, existem dois problemas principais:
- Primeiro (direto ou para o futuro) problema geodésico
- Dadas as coordenadas de um ponto e o direcional (azimute) e distância a um segundo ponto, determinar as coordenadas desse segundo ponto.
- Segundo (inverso ou reverso reverso) problema geodésico
- Dadas as coordenadas de dois pontos, determine o azimute e o comprimento da linha (estratura, curva ou geodésica) conectando esses pontos.
As soluções para ambos os problemas em geometria plana se reduzem a trigonometria simples e são válidas para pequenas áreas na superfície da Terra; em uma esfera, as soluções tornam-se significativamente mais complexas como, por exemplo, no problema inverso, os azimutes diferem indo entre os dois pontos finais ao longo do arco do grande círculo que os conecta.
A solução geral é chamada de geodésica para a superfície considerada, e as equações diferenciais para a geodésica podem ser resolvidas numericamente. No elipsóide de revolução, as geodésicas são expressas em termos de integrais elípticas, que geralmente são avaliadas em termos de uma expansão em série — veja, por exemplo, as fórmulas de Vincenty.
Conceitos de observação
Conforme definido na geodésia (e também na astronomia), alguns conceitos básicos de observação, como ângulos e coordenadas, incluem (mais comumente do ponto de vista de um observador local):
- Linha de produção ou vertical: (a linha ao longo) a direção da gravidade local.
- Zenith.: a (direção para a) interseção do vetor de gravidade para cima-extendente em um ponto e a esfera celestial.
- Nadir: o (direção para o) ponto antipodal onde o vetor de gravidade descendente-extendente interseta a esfera celestial (obscurada).
- horizonte celestial: um plano perpendicular ao vetor de gravidade em um ponto.
- Azimuth: o ângulo de direção dentro do plano do horizonte, tipicamente contado no sentido horário do norte (em geodésia e astronomia) ou o sul (em França).
- Elevação: a altura angular de um objeto acima do horizonte; alternativamente: zenith distância igual a 90 graus menos elevação.
- Coordenadas topocêntricas locais: azimuth (ângulo de direção dentro do plano do horizonte), ângulo de elevação (ou ângulo zenith), distância.
- Pólo celestial Norte: a extensão do eixo de rotação instantâneo da Terra (precessante e nutante) estendido para o norte para intersetar a esfera celestial. (Similarly para o polo celestial sul.)
- Equador Celestial: a interseção (instantânea) do plano equatorial da Terra com a esfera celestial.
- Plano de Meridiana: qualquer plano perpendicular ao equador celestial e contendo os pólos celestes.
- Meridiano local: o plano que contém a direção para o zenith e o pólo celestial.
Medidas
A superfície de referência (nível) usada para determinar diferenças de altura e sistemas de referência de altura é conhecida como nível médio do mar. O nível de bolha tradicional produz diretamente tais (para fins práticos mais úteis) alturas acima do nível do mar; o uso mais econômico de instrumentos GPS para determinação de altura requer um conhecimento preciso da figura do geóide, pois o GPS fornece apenas alturas acima do elipsóide de referência GRS80. À medida que a determinação do geóide melhora, pode-se esperar que o uso do GPS na determinação da altura também aumente.
O teodolito é um instrumento usado para medir ângulos horizontais e verticais (em relação à vertical local) para atingir pontos. Além disso, o taquímetro determina, eletronicamente ou eletro-opticamente, a distância até um alvo e é altamente automatizado ou mesmo robótico em operações. Amplamente utilizado para o mesmo fim é o método de posição de estação livre.
Comumente para levantamentos de detalhes locais, taquímetros são empregados, embora a técnica retangular antiquada usando um prisma de ângulo e fita de aço ainda seja uma alternativa barata. Como mencionado, também existem técnicas GPS cinemáticas em tempo real (RTK) rápidas e relativamente precisas. Os dados coletados são marcados e registrados digitalmente para entrada em bancos de dados do Sistema de Informação Geográfica (GIS).
Receptores geodésicos GNSS (mais comumente GPS) produzem diretamente coordenadas 3D em um quadro de coordenadas geocêntricas. Um desses quadros é o WGS84, bem como os quadros do Serviço Internacional de Sistemas de Referência e Rotação da Terra (IERS). Os receptores GNSS substituíram quase completamente os instrumentos terrestres para levantamentos de rede de base em grande escala.
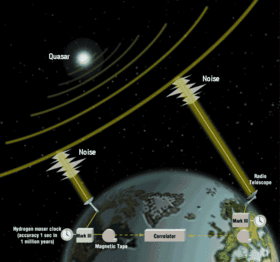
Para monitorar as irregularidades de rotação da Terra e os movimentos das placas tectônicas e para levantamentos geodésicos em todo o planeta, métodos de interferometria de linha de base muito longa (VLBI) medindo distâncias para quasares, alcance de laser lunar (LLR) medindo distâncias para prismas na Lua e distâncias de medição de alcance a laser por satélite (SLR) para prismas em satélites artificiais.
A gravidade é medida usando gravímetros, dos quais existem dois tipos. Os primeiros são os gravímetros absolutos, baseados na medição da aceleração de queda livre (por exemplo, de um prisma refletor em um tubo de vácuo). Eles são usados para estabelecer o controle geoespacial vertical ou no campo. Em segundo lugar, os gravímetros relativos são baseados em molas e são mais comuns. Eles são usados em levantamentos gravimétricos em grandes áreas — para estabelecer a figura do geóide nessas áreas. Os gravímetros relativos mais precisos são chamados de supercondutores" gravímetros, que são sensíveis a um milésimo de um bilionésimo da gravidade da superfície da Terra. Vinte e poucos gravímetros supercondutores são usados em todo o mundo no estudo das marés, rotação, carregamento interior, oceânico e atmosférico da Terra, bem como na verificação da constante gravitacional newtoniana.
No futuro, a gravidade e a altitude podem se tornar mensuráveis usando o conceito relativístico especial de dilatação do tempo medido por relógios ópticos.
Unidades e medidas no elipsóide
Latitude e longitude geográfica são indicadas em unidades de grau, minuto de arco e segundo de arco. Eles são ângulos, não métricos medidas e descreva a direção da normal local para o elipsóide de revolução de referência. Esta direção é aproximadamente a mesma que a direção do prumo, ou seja, a gravidade local, que também é a normal à superfície do geóide. Por esta razão, a determinação da posição astronômica – medindo a direção do prumo por meios astronômicos – funciona razoavelmente bem quando se usa também um modelo elipsoidal da figura da Terra.
Uma milha geográfica, definida como um minuto de arco no equador, equivale a 1.855,32571922 m. Uma milha náutica é um minuto de latitude astronômica. O raio de curvatura do elipsóide varia com a latitude, sendo o mais longo no pólo e o mais curto no equador, assim como na milha náutica.
Um metro foi originalmente definido como a décima milionésima parte do comprimento do equador ao Pólo Norte ao longo do meridiano que passa por Paris (o objetivo não foi totalmente alcançado na implementação real, pois está errado em 200 ppm na atual definições). Essa situação significa que um quilômetro equivale aproximadamente a (1/40.000) * 360 * 60 minutos meridionais de arco, ou 0,54 milhas náuticas. (Observe que não é bem assim porque as duas unidades foram definidas em bases diferentes, então a milha náutica internacional é exatamente 1.852 m, o que corresponde ao arredondamento de 1.000/0,54 m para quatro dígitos).
Mudanças temporais
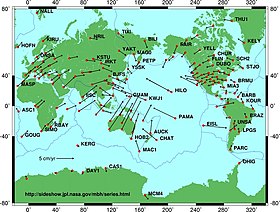
Várias técnicas são usadas em geodésia para estudar superfícies que mudam temporalmente, corpos de massa, campos físicos e sistemas dinâmicos. Pontos na superfície da Terra mudam de localização devido a uma variedade de mecanismos:
- Movimento de placa continental, placas tectônicas
- O movimento episódico da origem tectônica, especialmente perto de linhas de falha
- Efeitos periódicos devido a marés e carregamento de maré
- Levantamento de terra pós-glacial devido ao ajuste isostático
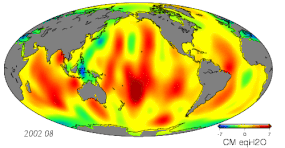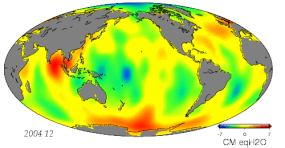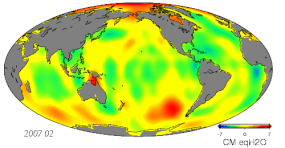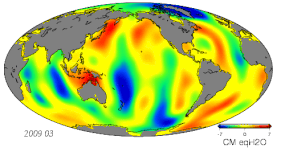
- Variações em massa devido a mudanças hidrológicas, incluindo a atmosfera, criosfera, hidrologia terrestre e oceanos
- Movimento polar subdiário
- Variabilidade de comprimento do dia
- Variações de centro de massa (geocentro) da Terra
- Movimentos antropogênicos como construção de reservatórios ou extração de petróleo ou água
Geodinâmica é a disciplina que estuda as deformações e movimentos da crosta terrestre e sua solidez como um todo. Freqüentemente, o estudo da rotação irregular da Terra está incluído na definição acima. Os estudos geodinâmicos requerem referenciais terrestres realizados pelas estações pertencentes ao Sistema Global de Observação Geodésica (GGOS).
As técnicas para estudar fenômenos geodinâmicos em escala global incluem:
- Posicionamento por satélite por GPS, GLONASS, Galileo e BeiDou
- Interferometria de linha muito longa (VLBI)
- Laser de satélite variando (SLR) e laser lunar variando (LLR)
- DOIS
- nivelamento regional e localmente preciso
- Taquímetros precisos
- Monitoramento da mudança de gravidade usando a gravimetria terrestre, aerotransportada, transmitida pelo navio e transmitida pelo espaço
- Altimetry satélite com base em micro-ondas e observações a laser para estudar a superfície do oceano, elevação do nível do mar e monitoramento da cobertura do gelo
- radar de abertura sintético interferométrico (InSAR) usando imagens de satélite.
Geodesistas notáveis
Contenido relacionado
Terra
Geografia de Kiribati
Ilhas Juan Fernández