Função gama

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Extensão da função factorial

Na matemática, a função gama (representada por $Γ$ , a letra maiúscula gama do alfabeto grego) é uma extensão comumente usada do fatorial função para números complexos. A função gama é definida para todos os números complexos, exceto os inteiros não positivos. Para cada inteiro positivo $n$ ,

{displaystyle Gamma (n)=(n-1)!,.}

Derivada por Daniel Bernoulli, para números complexos com parte real positiva, a função gama é definida por meio de uma integral imprópria convergente:

0,.}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">)) (zangão.)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∫ ∫ 0∞ ∞ )zangão.- Sim. - Sim. 1e- Sim. - Sim. )D),R R (zangão.)>0.Não. Gamma (z)=int _{0}^{infty }t^{z-1}e^{-t},dt,qquad Re (z)>0,.}0,.}" aria-hidden="true" class="mwe-math-fallback-image-display" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/496352155010f925f8583f4d22d157c333cc73b9" style="vertical-align: -2.338ex; width:38.124ex; height:5.843ex;"/>

A função gama é então definida como a continuação analítica desta função integral para uma função meromorfa que é holomorfa em todo o plano complexo, exceto zero e os inteiros negativos, onde a função tem pólos simples.

A função gama não tem zeros, então a função gama recíproca $1 / Γ(z)$ é uma função inteira. De fato, a função gama corresponde à transformada de Mellin da função exponencial negativa:

{displaystyle Gamma (z)={mathcal {M}}{e^{-x}}(z),.}

Existem outras extensões da função fatorial, mas a função gama é a mais popular e útil. É um componente em várias funções de distribuição de probabilidade e, como tal, é aplicável nos campos de probabilidade e estatística, bem como combinatória.

Motivação

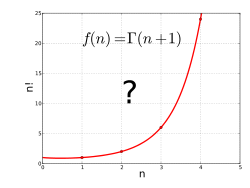
A função gama interpola a função fatorial aos valores não inteiros.

A função gama pode ser vista como uma solução para o seguinte problema de interpolação:

"Encontrar uma curva suave que conecta os pontos

(x, Sim.)

por

Sim. Não. x - 1)!

nos valores inteiros positivos para

x

Um gráfico dos primeiros fatoriais sugere que tal curva pode ser desenhada, mas seria preferível ter uma fórmula que descreva precisamente a curva, na qual o número de operações não depende do tamanho da x. A fórmula simples para o fatorial, $x! = 1 \times 2 \times \dots \times x$ , não pode ser usado diretamente para valores não inteiros de $x$ pois só é válido quando $x$ é um número natural (ou inteiro positivo). Não existem, relativamente falando, tais soluções simples para fatoriais; nenhuma combinação finita de somas, produtos, potências, funções exponenciais ou logaritmos será suficiente para expressar $x!$ ; mas é possível encontrar uma fórmula geral para fatoriais usando ferramentas como integrais e limites do cálculo. Uma boa solução para isso é a função gama.

Existem infinitas extensões contínuas do fatorial para não inteiros: infinitas curvas podem ser desenhadas através de qualquer conjunto de pontos isolados. A função gama é a solução mais útil na prática, sendo analítica (exceto nos inteiros não positivos), e pode ser definida de várias maneiras equivalentes. No entanto, não é a única função analítica que estende o fatorial, pois adiciona a ela qualquer função analítica que seja zero nos inteiros positivos, como $k sin mπx$ para um inteiro $m$ , dará outra função com essa propriedade. Tal função é conhecida como função pseudogama, sendo a mais famosa a função de Hadamard.

A função gama,

) zangão.)

em azul, traçado junto com

) zangão.) + pecado(π) zangão.)

em verde. Observe a interseção em inteiros positivos. Ambos são válidos continuações analíticas dos fatores para os não inteiros.

Uma propriedade mais restritiva do que satisfazer a interpolação acima é satisfazer a relação de recorrência definindo uma versão traduzida da função fatorial,

{displaystyle f(1)=1,}

{displaystyle f(x+1)=xf(x),}

para qualquer número real positivo $x$ . Mas isso permitiria a multiplicação por qualquer função $g (x)$ satisfazendo ambos $g (x) = g (x +1)$ para todos os números reais $x$ e $g (0) = 1$ , como a função $g (x) = e k pecado 2mπx$ . Uma das várias maneiras de resolver a ambiguidade vem do teorema de Bohr-Mollerup. Diz que quando a condição de $f$ ser logaritmicamente convex (ou "superconvex", o que significa que ${displaystyle ln circ f}$ é convexo) é adicionado, ele determina exclusivamente $f$ para entradas positivas e reais. A partir daí, a função gama pode ser estendida a todos os valores reais e complexos (exceto os inteiros negativos e zero) usando a continuação analítica única de $f$ .

Definição

Definição principal

A notação $Gamma (z)$ é devido a Legendre. Se a parte real do número complexo $zangão.$ é estritamente positivo ( $0}" xmlns="http://www.w3.org/1998/Math/MathML">R R (zangão.)>0{displaystyle Re (z)>0}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/df572a34b3badc29688f896ef60b7edacc835de5" style="vertical-align: -0.838ex; width:9.083ex; height:2.843ex;"/>$ ), então a integral

{displaystyle Gamma (z)=int _{0}^{infty }t^{z-1}e^{-t},dt}

converge absolutamente e é conhecida como a integral de Euler de segundo tipo. (A integral de Euler de primeiro tipo é a função beta.) Usando a integração por partes, vê-se que:

Lote de função gama em plano complexo em 3D com cores e lenda e 1000 pontos de enredo criados com Mathematica

{displaystyle {begin{aligned}Gamma (z+1)&=int _{0}^{infty }t^{z}e^{-t},dt\&={Bigl [}-t^{z}e^{-t}{Bigr ]}_{0}^{infty }+int _{0}^{infty }zt^{z-1}e^{-t},dt\&=lim _{tto infty }left(-t^{z}e^{-t}right)-left(-0^{z}e^{-0}right)+zint _{0}^{infty }t^{z-1}e^{-t},dt.end{aligned}}}

Reconhecendo que ${displaystyle -t^{z}e^{-t}to 0}$ como ${displaystyle tto infty}$

{displaystyle {begin{aligned}Gamma (z+1)&=zint _{0}^{infty }t^{z-1}e^{-t},dt\&=zGamma (z).end{aligned}}}

Podemos calcular ${displaystyle Gamma (1)}$ :

{displaystyle {begin{aligned}Gamma (1)&=int _{0}^{infty }t^{1-1}e^{-t},dt\&=int _{0}^{infty }e^{-t},dt\&=1.end{aligned}}}

Assim podemos mostrar que $Gamma (n)=(n-1)!$ para qualquer inteiro positivo $n$ por indução. Especificamente, o caso base é que ${displaystyle Gamma (1)=1=0!}$ , e o passo de indução é que ${displaystyle Gamma (n+1)=nGamma (n)=n(n-1)!=n!}$ .

A identidade ${textstyle Gamma (z)={frac {Gamma (z+1)}{z}}}$ pode ser usado (ou, produzindo o mesmo resultado, a continuação analítica pode ser usada) para estender exclusivamente a formulação integral para $Gamma (z)$ para uma função meromórfica definida para todos os números complexos $zangão.$ , exceto inteiros menos do que ou igual a zero. É esta versão estendida que é comumente referido como a função gama.

Definições alternativas

Definição de Euler como um produto infinito

Para um inteiro fixo $m$ , como o inteiro $n$ aumentos, temos que

{displaystyle lim _{nto infty }{frac {n!,left(n+1right)^{m}}{(n+m)!}}=1,.}

Se $m$ não é um inteiro, então não é possível dizer se esta equação é verdadeira porque ainda não temos (nesta seção) definiu a função fatorial para não inteiros. No entanto, temos uma extensão única da função fatorial para os não inteiros, insistindo que esta equação continua a segurar quando a inteiro arbitrário $m$ é substituído por um número complexo arbitrário $z$ ,

{displaystyle lim _{nto infty }{frac {n!,left(n+1right)^{z}}{(n+z)!}}=1,.}

{displaystyle (z-1)!}

{displaystyle {begin{aligned}Gamma (z)&=(z-1)!\[8pt]&={frac {1}{z}}lim _{nto infty }n!{frac {z!}{(n+z)!}}(n+1)^{z}\[8pt]&={frac {1}{z}}lim _{nto infty }(1cdots n){frac {1}{(1+z)cdots (n+z)}}left({frac {2}{1}}cdot {frac {3}{2}}cdots {frac {n+1}{n}}right)^{z}\[8pt]&={frac {1}{z}}prod _{n=1}^{infty }left[{frac {1}{1+{frac {z}{n}}}}left(1+{frac {1}{n}}right)^{z}right].end{aligned}}}

z

Gamma (z)

Gamma (n+1)=n!

n

{displaystyle (n+1)^{z}}

{displaystyle Gamma (n+z+1)}

{displaystyle Gamma (x+1)=xGamma (x)}

n+1

Gamma (z)

n

Definição de Weierstrass

A definição da função gama devido a Weierstrass também é válida para todos os números complexos $z$ exceto os inteiros não positivos:

{displaystyle Gamma (z)={frac {e^{-gamma z}}{z}}prod _{n=1}^{infty }left(1+{frac {z}{n}}right)^{-1}e^{z/n},}

{displaystyle gamma approx 0.577216}

{displaystyle 1/Gamma (z)}

Uma prova simples do produto é a seguinte:

${displaystyle Gamma (s)=lim _{nto infty }{frac {n!}{sleft(s+1right)...left(s+nright)}}n^{s}}$

${displaystyle =lim _{nto infty }{frac {1}{sleft(1+sright)left(1+{frac {s}{2}}right)...left(1+{frac {s}{n}}right)}}e^{sln left(nright)}}$

${displaystyle =lim _{nto infty }e^{sleft(ln left(nright)-1-{frac {1}{2}}-{frac {1}{3}}-...-{frac {1}{n}}right)}{frac {e^{sleft(1+{frac {1}{2}}+{frac {1}{3}}+...+{frac {1}{n}}right)}}{sleft(1+sright)left(1+{frac {s}{2}}right)...left(1+{frac {s}{n}}right)}}}$

${displaystyle ={frac {e^{-gamma s}}{s}}lim _{nto infty }prod _{k=1}^{n}left(1+{frac {s}{k}}right)^{-1}e^{frac {s}{k}}}$

Onde o fato de que ${displaystyle gamma =lim _{nto infty }left(sum _{k=1}^{n}{frac {1}{k}}-ln left(nright)right)}$ foi usado na última linha.

Propriedades

Geral

Outras equações funcionais importantes para a função gama são a fórmula de reflexão de Euler

{displaystyle Gamma (1-z)Gamma (z)={frac {pi }{sin pi z}},qquad znot in mathbb {Z} }

o que implica

{displaystyle Gamma (z-n)=(-1)^{n-1};{frac {Gamma (-z)Gamma (1+z)}{Gamma (n+1-z)}},qquad nin mathbb {Z} }

e a fórmula de duplicação de Legendre

{displaystyle Gamma (z)Gamma left(z+{tfrac {1}{2}}right)=2^{1-2z};{sqrt {pi }};Gamma (2z).}

Derivação da fórmula de reflexão de Euler
Desde então ${displaystyle e^{-t}=lim _{nto infty }left(1-{frac {t}{n}}right)^{n},}$ a função gamma pode ser representada como ${displaystyle Gamma (z)=lim _{nto infty }int _{0}^{n}t^{z-1}left(1-{frac {t}{n}}right)^{n},dt.}$ Integrando por peças $n$ tempos de rendimento ${displaystyle Gamma (z)=lim _{nto infty }{frac {n}{nz}}cdot {frac {n-1}{n(z+1)}}cdot {frac {n-2}{n(z+2)}}cdots {frac {1}{n(z+n-1)}}int _{0}^{n}t^{z+n-1},dt,}$ que é igual a ${displaystyle Gamma (z)=lim _{nto infty }{frac {n!}{n^{n}}}left(prod _{k=0}^{n}(z+k)^{-1}right)n^{z+n}.}$ Isso pode ser reescrito como ${displaystyle Gamma (z)=lim _{nto infty }{frac {n^{z}}{z}}prod _{k=1}^{n}{frac {k}{z+k}}=lim _{nto infty }{frac {n^{z}}{z}}prod _{k=1}^{n}{frac {1}{1+{frac {z}{k}}}}.}$ Podemos usar isso para avaliar o lado esquerdo da fórmula de reflexão: ${displaystyle Gamma (1-z)Gamma (z)=-zGamma (-z)Gamma (z)=lim _{nto infty }{frac {1}{z}}prod _{k=1}^{n}{frac {1}{1-{frac {z^{2}}{k^{2}}}}}.}$ Pode ser provado que ${displaystyle sin pi z=pi zprod _{k=1}^{infty }left(1-{frac {z^{2}}{k^{2}}}right).}$ Então... ${displaystyle {frac {pi }{sin pi z}}=lim _{nto infty }{frac {1}{z}}prod _{k=1}^{n}{frac {1}{1-{frac {z^{2}}{k^{2}}}}}.}$ A fórmula de reflexão de Euler segue: ${displaystyle Gamma (1-z)Gamma (z)={frac {pi }{sin pi z}},qquad znot in mathbb {Z}.}$

Derivação da fórmula de reflexão de Euler

Desde então ${displaystyle e^{-t}=lim _{nto infty }left(1-{frac {t}{n}}right)^{n},}$

a função gamma pode ser representada como

{displaystyle Gamma (z)=lim _{nto infty }int _{0}^{n}t^{z-1}left(1-{frac {t}{n}}right)^{n},dt.}

Integrando por peças $n$ tempos de rendimento

{displaystyle Gamma (z)=lim _{nto infty }{frac {n}{nz}}cdot {frac {n-1}{n(z+1)}}cdot {frac {n-2}{n(z+2)}}cdots {frac {1}{n(z+n-1)}}int _{0}^{n}t^{z+n-1},dt,}

que é igual a

{displaystyle Gamma (z)=lim _{nto infty }{frac {n!}{n^{n}}}left(prod _{k=0}^{n}(z+k)^{-1}right)n^{z+n}.}

Isso pode ser reescrito como

{displaystyle Gamma (z)=lim _{nto infty }{frac {n^{z}}{z}}prod _{k=1}^{n}{frac {k}{z+k}}=lim _{nto infty }{frac {n^{z}}{z}}prod _{k=1}^{n}{frac {1}{1+{frac {z}{k}}}}.}

Podemos usar isso para avaliar o lado esquerdo da fórmula de reflexão:

{displaystyle Gamma (1-z)Gamma (z)=-zGamma (-z)Gamma (z)=lim _{nto infty }{frac {1}{z}}prod _{k=1}^{n}{frac {1}{1-{frac {z^{2}}{k^{2}}}}}.}

Pode ser provado que

{displaystyle sin pi z=pi zprod _{k=1}^{infty }left(1-{frac {z^{2}}{k^{2}}}right).}

Então...

{displaystyle {frac {pi }{sin pi z}}=lim _{nto infty }{frac {1}{z}}prod _{k=1}^{n}{frac {1}{1-{frac {z^{2}}{k^{2}}}}}.}

A fórmula de reflexão de Euler segue:

{displaystyle Gamma (1-z)Gamma (z)={frac {pi }{sin pi z}},qquad znot in mathbb {Z}.}

Derivação da fórmula de duplicação Legendre
A função beta pode ser representada como ${displaystyle mathrm {B} (z_{1},z_{2})={frac {Gamma (z_{1})Gamma (z_{2})}{Gamma (z_{1}+z_{2})}}=int _{0}^{1}t^{z_{1}-1}(1-t)^{z_{2}-1},dt.}$ Configuração ${displaystyle z_{1}=z_{2}=z}$ produção ${displaystyle {frac {Gamma ^{2}(z)}{Gamma (2z)}}=int _{0}^{1}t^{z-1}(1-t)^{z-1},dt.}$ Após a substituição ${displaystyle t={frac {1+u}{2}}}$ nós temos ${displaystyle {frac {Gamma ^{2}(z)}{Gamma (2z)}}={frac {1}{2^{2z-1}}}int _{-1}^{1}left(1-u^{2}right)^{z-1},du.}$ A função ${displaystyle (1-u^{2})^{z-1}}$ é mesmo, portanto ${displaystyle 2^{2z-1}Gamma ^{2}(z)=2Gamma (2z)int _{0}^{1}(1-u^{2})^{z-1},du.}$ Agora assuma. ${displaystyle mathrm {B} left({frac {1}{2}},zright)=int _{0}^{1}t^{{frac {1}{2}}-1}(1-t)^{z-1},dt,quad t=s^{2}.}$ Então... ${displaystyle mathrm {B} left({frac {1}{2}},zright)=2int _{0}^{1}(1-s^{2})^{z-1},ds=2int _{0}^{1}(1-u^{2})^{z-1},du.}$ Isso implica ${displaystyle 2^{2z-1}Gamma ^{2}(z)=Gamma (2z)mathrm {B} left({frac {1}{2}},zright).}$ Desde então ${displaystyle mathrm {B} left({frac {1}{2}},zright)={frac {Gamma left({frac {1}{2}}right)Gamma (z)}{Gamma left(z+{frac {1}{2}}right)}},quad Gamma left({frac {1}{2}}right)={sqrt {pi }},}$ a fórmula de duplicação Legendre segue: ${displaystyle Gamma (z)Gamma left(z+{frac {1}{2}}right)=2^{1-2z}{sqrt {pi }};Gamma (2z).}$

Derivação da fórmula de duplicação Legendre

A função beta pode ser representada como

{displaystyle mathrm {B} (z_{1},z_{2})={frac {Gamma (z_{1})Gamma (z_{2})}{Gamma (z_{1}+z_{2})}}=int _{0}^{1}t^{z_{1}-1}(1-t)^{z_{2}-1},dt.}

Configuração ${displaystyle z_{1}=z_{2}=z}$ produção

{displaystyle {frac {Gamma ^{2}(z)}{Gamma (2z)}}=int _{0}^{1}t^{z-1}(1-t)^{z-1},dt.}

Após a substituição ${displaystyle t={frac {1+u}{2}}}$ nós temos

{displaystyle {frac {Gamma ^{2}(z)}{Gamma (2z)}}={frac {1}{2^{2z-1}}}int _{-1}^{1}left(1-u^{2}right)^{z-1},du.}

A função ${displaystyle (1-u^{2})^{z-1}}$ é mesmo, portanto

{displaystyle 2^{2z-1}Gamma ^{2}(z)=2Gamma (2z)int _{0}^{1}(1-u^{2})^{z-1},du.}

Agora assuma.

{displaystyle mathrm {B} left({frac {1}{2}},zright)=int _{0}^{1}t^{{frac {1}{2}}-1}(1-t)^{z-1},dt,quad t=s^{2}.}

Então...

{displaystyle mathrm {B} left({frac {1}{2}},zright)=2int _{0}^{1}(1-s^{2})^{z-1},ds=2int _{0}^{1}(1-u^{2})^{z-1},du.}

Isso implica

{displaystyle 2^{2z-1}Gamma ^{2}(z)=Gamma (2z)mathrm {B} left({frac {1}{2}},zright).}

Desde então

{displaystyle mathrm {B} left({frac {1}{2}},zright)={frac {Gamma left({frac {1}{2}}right)Gamma (z)}{Gamma left(z+{frac {1}{2}}right)}},quad Gamma left({frac {1}{2}}right)={sqrt {pi }},}

a fórmula de duplicação Legendre segue:

{displaystyle Gamma (z)Gamma left(z+{frac {1}{2}}right)=2^{1-2z}{sqrt {pi }};Gamma (2z).}

A fórmula de duplicação é um caso especial do teorema da multiplicação (consulte Eq. 5.5.6):

{displaystyle prod _{k=0}^{m-1}Gamma left(z+{frac {k}{m}}right)=(2pi)^{frac {m-1}{2}};m^{{frac {1}{2}}-mz};Gamma (mz).}

Uma propriedade simples, mas útil, que pode ser vista na definição de limite, é:

{displaystyle {overline {Gamma (z)}}=Gamma ({overline {z}});Rightarrow ;Gamma (z)Gamma ({overline {z}})in mathbb {R}.}

Em particular, com $z = a + bi$ , este produto é

{displaystyle |Gamma (a+bi)|^{2}=|Gamma (a)|^{2}prod _{k=0}^{infty }{frac {1}{1+{frac {b^{2}}{(a+k)^{2}}}}}}

Se a parte real for um número inteiro ou semi-inteiro, isso pode ser expresso finitamente na forma fechada:

{displaystyle {begin{aligned}|Gamma (bi)|^{2}&={frac {pi }{bsinh pi b}}\[6pt]left|Gamma left({tfrac {1}{2}}+biright)right|^{2}&={frac {pi }{cosh pi b}}\left|Gamma left(1+biright)right|^{2}&={frac {pi b}{sinh pi b}}\left|Gamma left(1+n+biright)right|^{2}&={frac {pi b}{sinh pi b}}prod _{k=1}^{n}left(k^{2}+b^{2}right),quad nin mathbb {N} \left|Gamma left(-n+biright)right|^{2}&={frac {pi }{bsinh pi b}}prod _{k=1}^{n}left(k^{2}+b^{2}right)^{-1},quad nin mathbb {N} \left|Gamma left({tfrac {1}{2}}pm n+biright)right|^{2}&={frac {pi }{cosh pi b}}prod _{k=1}^{n}left(left(k-{tfrac {1}{2}}right)^{2}+b^{2}right)^{pm 1},quad nin mathbb {N} end{aligned}}}

Prova de fórmulas de valor absoluto para argumentos de inteiro ou parte real de meio inteiro
Em primeiro lugar, considere a fórmula de reflexão aplicada a ${displaystyle z=bi}$ . ${displaystyle Gamma (bi)Gamma (1-bi)={frac {pi }{sin pi bi}}}$ Aplicando a relação de recorrência ao segundo termo, temos ${displaystyle -bicdot Gamma (bi)Gamma (-bi)={frac {pi }{sin pi bi}}}$ que com simples rearranjo dá ${displaystyle Gamma (bi)Gamma (-bi)={frac {pi }{-bisin pi bi}}={frac {pi }{bsinh pi b}}}$ Em segundo lugar, considere a fórmula de reflexão aplicada a ${displaystyle z={tfrac {1}{2}}+bi}$ . ${displaystyle Gamma ({tfrac {1}{2}}+bi)Gamma left(1-({tfrac {1}{2}}+bi)right)=Gamma ({tfrac {1}{2}}+bi)Gamma ({tfrac {1}{2}}-bi)={frac {pi }{sin pi ({tfrac {1}{2}}+bi)}}={frac {pi }{cos pi bi}}={frac {pi }{cosh pi b}}}$ Fórmulas para outros valores de $z$ para o qual a parte real é inteiro ou meio inteiro rapidamente seguir por indução usando a relação de recorrência nas direções positivas e negativas.

Prova de fórmulas de valor absoluto para argumentos de inteiro ou parte real de meio inteiro

Em primeiro lugar, considere a fórmula de reflexão aplicada a ${displaystyle z=bi}$ .

{displaystyle Gamma (bi)Gamma (1-bi)={frac {pi }{sin pi bi}}}

Aplicando a relação de recorrência ao segundo termo, temos

{displaystyle -bicdot Gamma (bi)Gamma (-bi)={frac {pi }{sin pi bi}}}

que com simples rearranjo dá

{displaystyle Gamma (bi)Gamma (-bi)={frac {pi }{-bisin pi bi}}={frac {pi }{bsinh pi b}}}

Em segundo lugar, considere a fórmula de reflexão aplicada a ${displaystyle z={tfrac {1}{2}}+bi}$ .

{displaystyle Gamma ({tfrac {1}{2}}+bi)Gamma left(1-({tfrac {1}{2}}+bi)right)=Gamma ({tfrac {1}{2}}+bi)Gamma ({tfrac {1}{2}}-bi)={frac {pi }{sin pi ({tfrac {1}{2}}+bi)}}={frac {pi }{cos pi bi}}={frac {pi }{cosh pi b}}}

Fórmulas para outros valores de $z$ para o qual a parte real é inteiro ou meio inteiro rapidamente seguir por indução usando a relação de recorrência nas direções positivas e negativas.

Talvez o valor mais conhecido da função gama em um argumento não inteiro seja

{displaystyle Gamma left({tfrac {1}{2}}right)={sqrt {pi }},}

que pode ser encontrado por definição ${textstyle z={frac {1}{2}}}$ nas fórmulas de reflexão ou duplicação, usando a relação com a função beta dada abaixo com ${textstyle z_{1}=z_{2}={frac {1}{2}}}$ , ou simplesmente fazendo a substituição ${displaystyle u={sqrt {z}}}$ na definição integral da função gama, resultando em uma integral gaussiana. Em geral, para valores inteiros não negativos $n$ nós temos:

{displaystyle {begin{aligned}Gamma left({tfrac {1}{2}}+nright)&={(2n)! over 4^{n}n!}{sqrt {pi }}={frac {(2n-1)!!}{2^{n}}}{sqrt {pi }}={binom {n-{frac {1}{2}}}{n}}n!{sqrt {pi }}\[8pt]Gamma left({tfrac {1}{2}}-nright)&={(-4)^{n}n! over (2n)!}{sqrt {pi }}={frac {(-2)^{n}}{(2n-1)!!}}{sqrt {pi }}={frac {sqrt {pi }}{{binom {-1/2}{n}}n!}}end{aligned}}}

onde o factorial duplo ${displaystyle (2n-1)!!=(2n-1)(2n-3)cdots (3)(1)}$ . Ver Valores particulares da função gama para valores calculados.

Pode ser tentador generalizar o resultado que ${textstyle Gamma left({frac {1}{2}}right)={sqrt {pi }}}$ procurando uma fórmula para outros valores individuais ${displaystyle Gamma (r)}$ Onde? $r$ é racional, especialmente porque de acordo com o teorema de punheta de Gauss, é possível fazê-lo para a função punheta intimamente relacionada a cada valor racional. No entanto, estes números ${displaystyle Gamma (r)}$ não são conhecidos por serem expressíveis por si mesmos em termos de funções elementares. Foi provado que ${displaystyle Gamma (n+r)}$ é um número transcendental e algébrica independente de $pi$ para qualquer inteiro $n$ e cada uma das frações ${textstyle r={frac {1}{6}},{frac {1}{4}},{frac {1}{3}},{frac {2}{3}},{frac {3}{4}},{frac {5}{6}}}$ . Em geral, quando os valores de computação da função gama, devemos nos contentar com aproximações numéricas.

As derivadas da função gama são descritas em termos da função poligama, $ψ (0) (z)$ :

{displaystyle Gamma '(z)=Gamma (z)psi ^{(0)}(z).}

Para um número inteiro positivo $m$ , a derivada da função gama pode ser calculada da seguinte forma:

Lote de função gama no plano complexo de

-2-2 Eu...

para

6+2 Eu...

com cores criadas no Mathematica

{displaystyle Gamma '(m+1)=m!left(-gamma +sum _{k=1}^{m}{frac {1}{k}}right)=m!left(-gamma +H(m)right),,}

onde H(m) é o m-ésimo número harmônico e $γ$ é a constante de Euler-Mascheroni.

Para $0}" xmlns="http://www.w3.org/1998/Math/MathML">R R (zangão.)>0{displaystyle Re (z)>0}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/df572a34b3badc29688f896ef60b7edacc835de5" style="vertical-align: -0.838ex; width:9.083ex; height:2.843ex;"/>$ o $n$ o derivado da função gama é:

{displaystyle {frac {d^{n}}{dz^{n}}}Gamma (z)=int _{0}^{infty }t^{z-1}e^{-t}(ln t)^{n},dt.}

(Isso pode ser derivado diferenciando a forma integral da função gama em relação a $z$ , e usando a técnica de diferenciação sob o signo integral.)

Usando a identidade

{displaystyle Gamma ^{(n)}(1)=(-1)^{n}n!sum limits _{pi ,vdash ,n},prod _{i=1}^{r}{frac {zeta ^{*}(a_{i})}{k_{i}!cdot a_{i}}}qquad zeta ^{*}(x):={begin{cases}zeta (x)&xneq 1\gamma &x=1end{cases}}}

Onde? $zeta (z)$ é a função zeta de Riemann, e $pi$ é uma partição de $n$ por

{displaystyle pi =underbrace {a_{1}+cdots +a_{1}} _{k_{1}{text{ terms}}}+cdots +underbrace {a_{r}+cdots +a_{r}} _{k_{r}{text{ terms}}},}

temos em particular a expansão em série de Laurent da função gama

{displaystyle Gamma (z)={frac {1}{z}}-gamma +{tfrac {1}{2}}left(gamma ^{2}+{frac {pi ^{2}}{6}}right)z-{tfrac {1}{6}}left(gamma ^{3}+{frac {gamma pi ^{2}}{2}}+2zeta (3)right)z^{2}+O(z^{3}).}

Desigualdades

Quando restrita aos números reais positivos, a função gama é uma função estritamente logaritmicamente convexa. Esta propriedade pode ser declarada em qualquer uma das três formas equivalentes a seguir:

Para qualquer dois números reais positivos $x_{1}$ e $x_{2}$ , e para qualquer ${displaystyle tin [0,1]}$ , ${displaystyle Gamma (tx_{1}+(1-t)x_{2})leq Gamma (x_{1})^{t}Gamma (x_{2})^{1-t}.}$
Para qualquer dois números reais positivos $x_{1}$ e $x_{2}$ e $x_{2}$ > $x_{1}$ $exp left({frac {Gamma '(x_{1})}{Gamma (x_{1})}}right).}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">()) (x2))) (x1))1x2- Sim. - Sim. x1>exp⁡ ⁡ ()) ?(x1))) (x1)).{displaystyle left({frac) (x_{2})}{Gamma (x_{1})}}right)^{frac {1}{x_{2}-x_{1}}}>exp left({frac {Gamma '(x_{1})}{Gamma (x_{1})}}right). ?exp left({frac {Gamma '(x_{1})}{Gamma (x_{1})}}right).}" aria-hidden="true" class="mwe-math-fallback-image-display" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/5194e6aa569d26e8025eca83bf940fb3d016129d" style="vertical-align: -2.671ex; width:33.023ex; height:7.509ex;"/>$
Para qualquer número real positivo $x$ , $Gamma '(x)^{2}.}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">)) "(x))) (x)>)) ?(x)2.{displaystyle Gamma '(x)Gamma (x)>Gamma '(x)^{2}.}Gamma '(x)^{2}.}" aria-hidden="true" class="mwe-math-fallback-image-display" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/4373886f42367359b96a6c4b0970322960afa6e4" style="vertical-align: -0.838ex; width:20.397ex; height:3.176ex;"/>$

A última dessas declarações é, essencialmente, por definição, a mesma que a declaração de que $0}" xmlns="http://www.w3.org/1998/Math/MathML">? ? (1)(x)>0(x)>0} 0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/29da945d1c0efd2dc669ae7e83e0c3503f178c1c" style="vertical-align: -0.838ex; width:11.247ex; height:3.343ex;"/>$ , onde ${displaystyle psi ^{(1)}}$ é a função de poligama da ordem 1. Para provar a convexidade logarítmica da função gama, é suficiente observar que ${displaystyle psi ^{(1)}}$ tem uma representação de série que, para real positivo $x$ , consiste em apenas termos positivos.

Convexidade logarítmica e desigualdade de Jensen juntos implicam, para qualquer número real positivo $x_{1},ldotsx_{n}$ e $a_1, ldots, a_n$ ,

{displaystyle Gamma left({frac {a_{1}x_{1}+cdots +a_{n}x_{n}}{a_{1}+cdots +a_{n}}}right)leq {bigl (}Gamma (x_{1})^{a_{1}}cdots Gamma (x_{n})^{a_{n}}{bigr)}^{frac {1}{a_{1}+cdots +a_{n}}}.}

Também há limites nas proporções de funções gama. A mais conhecida é a desigualdade de Gautschi, que diz que para qualquer número real positivo $x$ e qualquer $s \in (0, 1)$ ,

<math alttext="{displaystyle x^{1-s}<{frac {Gamma (x+1)}{Gamma (x+s)}}x1- Sim. - Sim. S<)) (x+1))) (x+S)<(x+1)1- Sim. - Sim. S.Não. x^{1-s} frac {Gamma (x+1)}{Gamma (x+s)}}<left(x+1right)^{1-s}.}<img alt="{displaystyle x^{1-s}<{frac {Gamma (x+1)}{Gamma (x+s)}}

Fórmula de Stirling

Representação da função gama no plano complexo. Cada ponto

z

é colorido de acordo com o argumento de

Gamma (z)

. O enredo de contorno do módulo

{displaystyle |Gamma (z)|}

também é exibido.

plotagem tridimensional do valor absoluto da função gama complexa

O comportamento de $Gamma(x)$ para uma variável real positiva crescente é dada pela fórmula de Stirling

{displaystyle Gamma (x+1)sim {sqrt {2pi x}}left({frac {x}{e}}right)^{x},}

sim

{textstyle xto +infty }

{displaystyle exp(beta x)}

beta

Outro limite útil para aproximações assintoticas para ${displaystyle xto +infty }$ é:

{displaystyle {Gamma (x+alpha)}sim {Gamma (x)x^{alpha }},qquad alpha in mathbb {C}.}

Resíduos

O comportamento para não positivo $z$ é mais intrincado. A integral de Euler não converge para ${displaystyle Re (z)leq 0}$ , mas a função que define no meio-plano complexo positivo tem uma continuação analítica única para o meio-plano negativo. Uma maneira de descobrir que a continuação analítica é usar a integral de Euler para argumentos positivos e estender o domínio para números negativos por aplicação repetida da fórmula de recorrência,

{displaystyle Gamma (z)={frac {Gamma (z+n+1)}{z(z+1)cdots (z+n)}},}

n

{displaystyle z+n}

z

{displaystyle 0,-1,-2,ldots }

Para uma função $f$ de uma variável complexa $z$ , em um poste simples $c$ , o resíduo de $f$ é dado por:

{displaystyle operatorname {Res} (f,c)=lim _{zto c}(z-c)f(z).}

Para o pólo simples ${displaystyle z=-n,}$ nós reescrevemos a fórmula de recorrência como:

{displaystyle (z+n)Gamma (z)={frac {Gamma (z+n+1)}{z(z+1)cdots (z+n-1)}}.}

{displaystyle z=-n,}

{displaystyle Gamma (z+n+1)=Gamma (1)=1}

{displaystyle z(z+1)cdots (z+n-1)=-n(1-n)cdots (n-1-n)=(-1)^{n}n!.}

{displaystyle operatorname {Res} (Gamma-n)={frac {(-1)^{n}}{n!}}.}

A função gamma é não-zero em todos os lugares ao longo da linha real, embora ele vem arbitrariamente perto de zero como $zangão. \to$ . Na verdade, não há número complexo $z$ para os quais ${displaystyle Gamma (z)=0}$ , e daí a função gama recíproca ${textstyle {frac {1}{Gamma (z)}}}$ é uma função inteira, com zeros em ${displaystyle z=0,-1,-2,ldots }$ .

Mínimos e máximos

Na linha real, a função gama tem um mínimo local em $z min \approx +1.46163 214496836234126$ onde atinge o valor $Γ(z min) \approx +0.88560 319441088870027$ . A função gama aumenta para qualquer um dos lados desse mínimo. A solução para $Γ(z - 0.5) = Γ(z + 0.5)$ é $z = +1,5$ e o valor comum é $Γ(1) = Γ(2) = +1$ . A solução positiva para $Γ(z - 1) = Γ(z + 1)$ é $z = φ \approx +1,618$ , a proporção áurea e o valor comum é $Γ(φ - 1) = Γ(φ + 1) = φ! \approx +1.44922 960226989660037$ .

A função gama deve alternar o sinal entre seus pólos nos inteiros não positivos porque o produto na recorrência dianteira contém um número estranho de fatores negativos se o número de pólos entre $z$ e ${displaystyle z+n}$ é estranho, e um número mesmo se o número de pólos é mesmo. Os valores extremos da função Gamma entre os inteiros não positivos são $) - 0,50408 3008264549 38526...) = - 3.54464 36155005 08912...$ , $) - 1.57349 8473162390 45877...) = 2.30240 7258339680 13582...$ , $) -2.61072 0868444144 650...) = -0.88813 6358401241 92009...$ , $) -3.63529 33636901 09783...) = 0,24512 7539834366 25043...$ , $) -4.65323 77617431 44171...) = -0.05277 969587319 40076...$ , etc.

Representações integrais

Existem muitas fórmulas, além da integral de Euler de segundo tipo, que expressam a função gama como uma integral. Por exemplo, quando a parte real de $z$ é positiva,

{displaystyle Gamma (z)=int _{-infty }^{infty }e^{zt-e^{t}},dt}

{displaystyle Gamma (z)=int _{0}^{1}left(log {frac {1}{t}}right)^{z-1},dt,}

{displaystyle Gamma (z)=2int _{0}^{infty }t^{2z-1}e^{-t^{2}},dt}

onde as três integrais seguem, respectivamente, das substituições ${displaystyle t=e^{-x}}$ , ${displaystyle t=-log x}$ e ${displaystyle t=x^{2}}$ na segunda integral de Euler. A última integral em particular deixa claro a conexão entre a função gama em meio argumentos inteiros e a integral gaussiana: se deixarmos ${displaystyle z=1/2}$ nós temos ${textstyle Gamma (1/2)={sqrt {pi }}=2int _{0}^{infty }e^{-t^{2}},dt}$ .

A primeira fórmula integral de Binet para a função gama afirma que, quando a parte real de $z$ é positiva, então:

{displaystyle log Gamma (z)=left(z-{frac {1}{2}}right)log z-z+{frac {1}{2}}log(2pi)+int _{0}^{infty }left({frac {1}{2}}-{frac {1}{t}}+{frac {1}{e^{t}-1}}right){frac {e^{-tz}}{t}},dt.}

{displaystyle log left(Gamma (z)left({frac {e}{z}}right)^{z}{sqrt {2pi z}}right)={mathcal {L}}left({frac {1}{2t}}-{frac {1}{t^{2}}}+{frac {1}{t(e^{t}-1)}}right)(z).}

A segunda fórmula integral de Binet afirma que, novamente, quando a parte real de $z$ é positiva, então:

{displaystyle log Gamma (z)=left(z-{frac {1}{2}}right)log z-z+{frac {1}{2}}ln(2pi)+2int _{0}^{infty }{frac {arctan(t/z)}{e^{2pi t}-1}},dt.}

Vamos. $C$ ser um contorno Hankel, significando um caminho que começa e termina no ponto $\infty$ na esfera de Riemann, cujo vetor tangente unitário converge para $- Sim.$ no início do caminho e $1$ no final, que tem enrolamento número 1 em torno $0$ , e que não cruza $[0, \infty]$ . Corrigir um ramo de ${displaystyle log(-t)}$ tomando um ramo cortado ao longo $[0, \infty]$ e tomando ${displaystyle log(-t)}$ para ser real quando $)$ está no eixo real negativo. Assumir $zangão.$ não é um inteiro. Então a fórmula de Hankel para a função gama é:

{displaystyle Gamma (z)=-{frac {1}{2isin pi z}}int _{C}(-t)^{z-1}e^{-t},dt,}

{displaystyle (-t)^{z-1}}

{displaystyle exp((z-1)log(-t))}

{displaystyle {frac {1}{Gamma (z)}}={frac {i}{2pi }}int _{C}(-t)^{-z}e^{-t},dt,}

zangão.

Representação de fração contínua

A função gama também pode ser representada por uma soma de duas frações contínuas:

{displaystyle Gamma (z)={cfrac {e^{-1}}{2+0-z+1{cfrac {z-1}{2+2-z+2{cfrac {z-2}{2+4-z+3{cfrac {z-3}{2+6-z+4{cfrac {z-4}{2+8-z+5{cfrac {z-5}{2+10-z+ddots }}}}}}}}}}}}+{cfrac {e^{-1}}{z+0-{cfrac {z+0}{z+1+{cfrac {1}{z+2-{cfrac {z+1}{z+3+{cfrac {2}{z+4-{cfrac {z+2}{z+5+{cfrac {3}{z+6-ddots }}}}}}}}}}}}}}}

zinmathbb{C}

Expansão da série de Fourier

O logaritmo da função gama tem a seguinte expansão da série Fourier para $<math alttext="{displaystyle 0<z0<zangão.<1:- Não. <img alt="{displaystyle 0<z$

{displaystyle ln Gamma (z)=left({frac {1}{2}}-zright)(gamma +ln 2)+(1-z)ln pi -{frac {1}{2}}ln sin(pi z)+{frac {1}{pi }}sum _{n=1}^{infty }{frac {ln n}{n}}sin(2pi nz),}

que por muito tempo foi atribuído a Ernst Kummer, que o derivou em 1847. No entanto, Iaroslav Blagouchine descobriu que Carl Johan Malmsten derivou pela primeira vez esta série em 1842.

Fórmula de Raabe

Em 1840, Joseph Ludwig Raabe provou que

0.}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">∫ ∫ umum+1I⁡ ⁡ )) (zangão.)Dzangão.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =12I⁡ ⁡ 2D D +umI⁡ ⁡ um- Sim. - Sim. um,um>0.{displaystyle int _{a}^{a+1}ln Gamma (z),dz={tfrac {1}{2}}ln 2pi +aln a-a,quad a>0.}0.}" aria-hidden="true" class="mwe-math-fallback-image-display" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/a80520ee00b22841dffdec890c712f8bddf06fe5" style="vertical-align: -2.338ex; width:46.964ex; height:6.176ex;"/>

a=0

{displaystyle int _{0}^{1}ln Gamma (z),dz={tfrac {1}{2}}ln 2pi.}

Este último pode ser derivado tomando o logaritmo na fórmula de multiplicação acima, que dá uma expressão para a soma de Riemann do integrando. Tomando o limite para $ato infty$ dá a fórmula.

Função Pi

Uma notação alternativa que foi originalmente introduzida por Gauss é a $Pi$ -função, que, em termos da função gama, é

{displaystyle Pi (z)=Gamma (z+1)=zGamma (z)=int _{0}^{infty }e^{-t}t^{z},dt,}

assim ${displaystyle Pi (n)=n!}$ para cada inteiro não negativo $n$ .

Usando a função pi, a fórmula de reflexão assume a forma

{displaystyle Pi (z)Pi (-z)={frac {pi z}{sin(pi z)}}={frac {1}{operatorname {sinc} (z)}}}

onde $sinc$ é a função sinc normalizada, enquanto o teorema da multiplicação assume a forma

{displaystyle Pi left({frac {z}{m}}right),Pi left({frac {z-1}{m}}right)cdots Pi left({frac {z-m+1}{m}}right)=(2pi)^{frac {m-1}{2}}m^{-z-{frac {1}{2}}}Pi (z).}

Às vezes também encontramos

{displaystyle pi (z)={frac {1}{Pi (z)}}}

que é uma função inteira, definida para cada número complexo, assim como a função gama recíproca. Isso. $pi (z)$ é inteiro implica que não tem pólos, então ${displaystyle Pi left(zright)}$ Como $Gamma left(zright)$ , não tem zeros.

O volume de um n-elipsóide com raios $r 1, \dots, r n$ pode ser expresso como

{displaystyle V_{n}(r_{1},dotscr_{n})={frac {pi ^{frac {n}{2}}}{Pi left({frac {n}{2}}right)}}prod _{k=1}^{n}r_{k}.}

Relação com outras funções

Na primeira integral acima, que define a função gama, os limites da integração são fixos. As funções gamas superiores e inferiores incompletas são as funções obtidas permitindo que o limite inferior ou superior (respectivamente) da integração possa variar.
A função gamma está relacionada à função beta pela fórmula ${displaystyle mathrm {B} (z_{1},z_{2})=int _{0}^{1}t^{z_{1}-1}(1-t)^{z_{2}-1},dt={frac {Gamma (z_{1}),Gamma (z_{2})}{Gamma (z_{1}+z_{2})}}.}$
O derivado logarítmico da função gama é chamado de função punção; derivados mais elevados são as funções de poligama.
O análogo da função gama sobre um campo finito ou um anel finito é as somas gaussianas, um tipo de soma exponencial.
A função gama recíproca é uma função inteira e tem sido estudada como um tópico específico.
A função gamma também aparece em uma relação importante com a função zeta de Riemann, ${displaystyle zeta (z)}$ . ${displaystyle pi ^{-{frac {z}{2}}};Gamma left({frac {z}{2}}right)zeta (z)=pi ^{-{frac {1-z}{2}}};Gamma left({frac {1-z}{2}}right);zeta (1-z).}$ Ele também aparece na seguinte fórmula: ${displaystyle zeta (z)Gamma (z)=int _{0}^{infty }{frac {u^{z}}{e^{u}-1}},{frac {du}{u}},}$ que é válido apenas para $1}" xmlns="http://www.w3.org/1998/Math/MathML">R R (zangão.)>1{displaystyle Re (z)>1}1}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1bee7b9b86cd9089719e48ddc68acd1940db5d5c" style="vertical-align: -0.838ex; width:9.083ex; height:2.843ex;"/>$ .
O logaritmo da função gama satisfaz a seguinte fórmula devido a Lerch: ${displaystyle log Gamma (z)=zeta _{H}'(0,z)-zeta '(0),}$ Onde? ${displaystyle zeta _{H}}$ é a função zeta de Hurwitz, $zeta$ é a função zeta Riemann e o primo ( $?$ ) denota a diferenciação na primeira variável.
A função gama está relacionada à função exponencial esticada. Por exemplo, os momentos dessa função são ${displaystyle langle tau ^{n}rangle equiv int _{0}^{infty }dt,t^{n-1},e^{-left({frac {t}{tau }}right)^{beta }}={frac {tau ^{n}}{beta }}Gamma left({n over beta }right).}$

Valores específicos

Incluindo até os primeiros 20 dígitos após o ponto decimal, alguns valores particulares da função gama são:

{displaystyle {begin{array}{rcccl}Gamma left(-{tfrac {3}{2}}right)&=&{tfrac {4{sqrt {pi }}}{3}}&approx &+2.36327,18012,07354,70306\Gamma left(-{tfrac {1}{2}}right)&=&-2{sqrt {pi }}&approx &-3.54490,77018,11032,05459\Gamma left({tfrac {1}{2}}right)&=&{sqrt {pi }}&approx &+1.77245,38509,05516,02729\Gamma (1)&=&0!&=&+1\Gamma left({tfrac {3}{2}}right)&=&{tfrac {sqrt {pi }}{2}}&approx &+0.88622,69254,52758,01364\Gamma (2)&=&1!&=&+1\Gamma left({tfrac {5}{2}}right)&=&{tfrac {3{sqrt {pi }}}{4}}&approx &+1.32934,03881,79137,02047\Gamma (3)&=&2!&=&+2\Gamma left({tfrac {7}{2}}right)&=&{tfrac {15{sqrt {pi }}}{8}}&approx &+3.32335,09704,47842,55118\Gamma (4)&=&3!&=&+6end{array}}}

\infty

{displaystyle {frac {1}{Gamma (-3)}}={frac {1}{Gamma (-2)}}={frac {1}{Gamma (-1)}}={frac {1}{Gamma (0)}}=0.}

A função log-gama

A função analítica

log Γ() zangão.)

Como as funções gama e fatorial crescem tão rapidamente para argumentos moderadamente grandes, muitos ambientes de computação incluem uma função que retorna o logaritmo natural da função gama (geralmente recebe o nome de lgamma ou lngamma em ambientes de programação ou gammaln em planilhas); isso cresce muito mais lentamente e, para cálculos combinatórios, permite adicionar e subtrair logs em vez de multiplicar e dividir valores muito grandes. Muitas vezes é definido como

{displaystyle ln Gamma (z)=-gamma z-ln z+sum _{k=1}^{infty }left[{frac {z}{k}}-ln left(1+{frac {z}{k}}right)right].}

A função digamma, que é a derivada desta função, também é comumente vista. No contexto de aplicações técnicas e físicas, por ex. com propagação de ondas, a equação funcional

{displaystyle ln Gamma (z)=ln Gamma (z+1)-ln z}

Lote de função gama logarítmica no plano complexo de -2-2i a 2+2i com cores criadas com função Mathematica 13.1 ComplexPlot3D

é frequentemente usado uma vez que permite determinar valores de função em uma faixa de largura 1 em $zangão.$ da tira vizinha. Em particular, começando com uma boa aproximação para uma $zangão.$ com grande parte real um pode ir passo a passo até o desejado $zangão.$ . Após uma indicação de Carl Friedrich Gauss, Rocktaeschel (1922) propôs para ${displaystyle ln(Gamma (z))}$ uma aproximação para grande $Re(zangão.)$ :

{displaystyle ln Gamma (z)approx (z-{tfrac {1}{2}})ln z-z+{tfrac {1}{2}}ln(2pi).}

Isso pode ser usado para aproximar com precisão $ln(Γ(z))$ para $z$ com um $Re(z)$ menor via (P.E.Böhmer, 1939)

{displaystyle ln Gamma (z-m)=ln Gamma (z)-sum _{k=1}^{m}ln(z-k).}

Uma aproximação mais precisa pode ser obtida usando mais termos das expansões assintóticas de $ln(Γ(z))$ e $Γ(z)$ , que são baseados na aproximação de Stirling.

{displaystyle Gamma (z)sim z^{z-{frac {1}{2}}}e^{-z}{sqrt {2pi }}left(1+{frac {1}{12z}}+{frac {1}{288z^{2}}}-{frac {139}{51,840z^{3}}}-{frac {571}{2,488,320z^{4}}}right)}

como

| zangão. | \to \infty

em constante

| Arg(zangão.) | < π

. (Ver sequências A001163 e A001164 no OEIS.)

De uma forma mais "natural" apresentação:

{displaystyle ln Gamma (z)=zln z-z-{tfrac {1}{2}}ln z+{tfrac {1}{2}}ln 2pi +{frac {1}{12z}}-{frac {1}{360z^{3}}}+{frac {1}{1260z^{5}}}+oleft({frac {1}{z^{5}}}right)}

como

| zangão. | \to \infty

em constante

| Arg(zangão.) | < π

. (Ver seqüências A046968 e A046969 no OEIS.)

Os coeficientes dos termos com $k > 1$ de $z 1- k$ na última expansão são simplesmente

{displaystyle {frac {B_{k}}{k(k-1)}}}

B k

A função Gama também tem a Série de Stirling (derivada por Charles Hermite em 1900) igual a

0.}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">log⁡ ⁡ )) (1+x)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =x(x- Sim. - Sim. 1)2!log⁡ ⁡ (2)+x(x- Sim. - Sim. 1)(x- Sim. - Sim. 2)3!(log⁡ ⁡ (3)- Sim. - Sim. 2log⁡ ⁡ (2))+⋯ ⋯ ,R R (x)>0.{displaystyle log Gamma (1+x)={frac {x(x-1)}{2!}}log(2)+{frac {x-1)(x-2)}{3!}}(log(3)-2log(2))+cdotsquad Re (x)>0.}0.}" aria-hidden="true" class="mwe-math-fallback-image-display" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/815acc690b8aaaf4e52444168abec2ae9537a572" style="vertical-align: -2.005ex; width:87.345ex; height:5.843ex;"/>

Propriedades

O teorema de Bohr–Mollerup afirma que entre todas as funções que estendem as funções fatoriais aos números reais positivos, apenas a função gama é log-convexa, ou seja, seu logaritmo natural é convexo no eixo real positivo. Outra caracterização é dada pelo teorema de Wielandt.

A função gama é a única função que satisfaz simultaneamente

$Gamma (1)=1$ ,
$Gamma (z+1)=zGamma (z)$ para todos os números complexos $z$ exceto os inteiros não positivos, e,
para o inteiro $n$ , ${textstyle lim _{nto infty }{frac {Gamma (n+z)}{Gamma (n);n^{z}}}=1}$ para todos os números complexos $z$ .

Em certo sentido, a função $ln(Γ)$ é a forma mais natural; torna alguns atributos intrínsecos da função mais claros. Um exemplo impressionante é a série de Taylor de $ln(Γ)$ em torno de 1:

<math alttext="{displaystyle ln Gamma (z+1)=-gamma z+sum _{k=2}^{infty }{frac {zeta (k)}{k}},(-z)^{k}qquad forall ;|z|I⁡ ⁡ )) (zangão.+1)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. γ γ zangão.+Gerenciamento Gerenciamento k= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2∞ ∞ ζ ζ (k)k(- Sim. - Sim. zangão.)kGerenciamento de contas Gerenciamento de contas |zangão.|<1{displaystyle ln Gamma (z+1)=-gamma z+sum _{k=2}^{infty }{frac {zeta (k)}{k}},(-z)^{k}qquad forall ;|z|<1}<img alt="{displaystyle ln Gamma (z+1)=-gamma z+sum _{k=2}^{infty }{frac {zeta (k)}{k}},(-z)^{k}qquad forall ;|z|

com $ζ (k)$ denotando a função Riemann zeta em $k$ .

Então, usando a seguinte propriedade:

{displaystyle zeta (s)Gamma (s)=int _{0}^{infty }{frac {t^{s}}{e^{t}-1}},{frac {dt}{t}}}

In(Γ)

{displaystyle ln Gamma (z+1)=-gamma z+int _{0}^{infty }{frac {,left(e^{-zt}-1+ztright),}{tleft(e^{t}-1right)}},dt}

ou, definindo $z = 1$ para obter uma integral para $γ$ , podemos substituir o termo $γ$ por sua integral e incorporá-lo à fórmula acima para obter:

{displaystyle ln Gamma (z+1)=int _{0}^{infty }{frac {,left(e^{-zt}-ze^{-t}-1+zright),}{t(e^{t}-1)}},dt,.}

Há também fórmulas especiais para o logaritmo da função gama para racional $zangão.$ . Por exemplo, se $k$ e $n$ são inteiros com $<math alttext="{displaystyle kk<n- Sim. <img alt="k$ e ${displaystyle kneq n/2,,}$ então

{displaystyle {begin{aligned}ln Gamma left({frac {k}{n}}right)={}&{frac {,(n-2k)ln 2pi ,}{2n}}+{frac {1}{2}}left{,ln pi -ln sin {frac {pi k}{n}},right}+{frac {1}{pi }}!sum _{r=1}^{n-1}{frac {,gamma +ln r,}{r}}cdot sin {frac {,2pi rk,}{n}}\&{}-{frac {1}{2pi }}sin {frac {2pi k}{n}}cdot !int _{0}^{infty }!!{frac {,e^{-nx}!cdot ln x,}{,cosh x-cos(2pi k/n),}},{mathrm {d} }xend{aligned}}}

ver. Essa fórmula às vezes é usada para computação numérica, pois o integrando diminui muito rapidamente.

Integração sobre log-gamma

A integral

{displaystyle int _{0}^{z}ln Gamma (x),dx}

pode ser expresso em termos da função G de Barnes (consulte a função G de Barnes para uma prova):

{displaystyle int _{0}^{z}ln Gamma (x),dx={frac {z}{2}}ln(2pi)+{frac {z(1-z)}{2}}+zln Gamma (z)-ln G(z+1)}

onde $Re(z) > -1$ .

Também pode ser escrito em termos da função zeta de Hurwitz:

{displaystyle int _{0}^{z}ln Gamma (x),dx={frac {z}{2}}ln(2pi)+{frac {z(1-z)}{2}}-zeta '(-1)+zeta '(-1,z).}

Quando $z=1$ segue:

{displaystyle int _{0}^{1}ln Gamma (x),dx={frac {1}{2}}ln(2pi),}

{displaystyle ln Gamma }

{displaystyle int _{0}^{1}ln ^{2}Gamma (x)dx={frac {gamma ^{2}}{12}}+{frac {pi ^{2}}{48}}+{frac {1}{3}}gamma L_{1}+{frac {4}{3}}L_{1}^{2}-left(gamma +2L_{1}right){frac {zeta ^{prime }(2)}{pi ^{2}}}+{frac {zeta ^{prime prime }(2)}{2pi ^{2}}},}

L_{1}

{displaystyle {frac {1}{2}}ln(2pi)}

D. H. Bailey e seus co-autores fizeram uma avaliação para

{displaystyle L_{n}:=int _{0}^{1}ln ^{n}Gamma (x),dx}

n=1,2

Além disso, também é sabido que

{displaystyle lim _{nto infty }{frac {L_{n}}{n!}}=1.}

Aproximações

Gamma de comparação (linha azul) com o fatorial (pontos azuis) e aproximação de Stirling (linha vermelha)

Valores complexos da função gama podem ser aproximados usando a aproximação de Stirling ou a aproximação de Lanczos,

<math alttext="{displaystyle Gamma (z)sim {sqrt {2pi }}z^{z-1/2}e^{-z}quad {hbox{as }}zto infty {hbox{ in }}left|arg(z)right|)) (zangão.)∼ ∼ 2D D zangão.zangão.- Sim. - Sim. 1/2e- Sim. - Sim. zangão.comozangão.→ → ∞ ∞ em|Arg⁡ ⁡ (zangão.)|<D D .Não. Gamma (z)sim {sqrt {2pi }}z^{z-1/2}e^{-z}quad {hbox{as }}zto infty {hbox{ in }}left|arg(z)right|<pi.}<img alt="{displaystyle Gamma (z)sim {sqrt {2pi }}z^{z-1/2}e^{-z}quad {hbox{as }}zto infty {hbox{ in }}left|arg(z)right|

| zangão. |

A função gama pode ser computada para precisão fixa para ${displaystyle operatorname {Re} (z)in [1,2]}$ aplicando a integração por partes à integral da Euler. Para qualquer número positivo $x$ a função gamma pode ser escrita

{displaystyle {begin{aligned}Gamma (z)&=int _{0}^{x}e^{-t}t^{z},{frac {dt}{t}}+int _{x}^{infty }e^{-t}t^{z},{frac {dt}{t}}\&=x^{z}e^{-x}sum _{n=0}^{infty }{frac {x^{n}}{z(z+1)cdots (z+n)}}+int _{x}^{infty }e^{-t}t^{z},{frac {dt}{t}}.end{aligned}}}

Quando $Re(zangão.) \in [1,2]$ e $x geq 1$ , o valor absoluto da última integral é menor do que ${displaystyle (x+1)e^{-x}}$ . Escolhendo um grande o suficiente $x$ , esta última expressão pode ser feita menor do que ${displaystyle 2^{-N}}$ para qualquer valor desejado $N$ . Assim, a função gamma pode ser avaliada para $N$ bits de precisão com a série acima.

Um algoritmo rápido para cálculo da função gama de Euler para qualquer argumento algébrico (incluindo racional) foi construído por E.A. Karatsuba.

Para argumentos que são múltiplos inteiros de $1 / 24$ , a função gama também pode ser avaliada rapidamente usando iterações médias aritméticas-geométricas (ver valores específicos da função gama).

Aplicativos

Um autor descreve a função gama como "Indiscutivelmente, a função especial mais comum, ou a menos 'especial' deles. As outras funções transcendentais [...] são chamadas de funções 'especiais' porque você poderia evitar alguns deles ficando longe de muitos tópicos matemáticos especializados. Por outro lado, a função gama $Γ(z)$ é a mais difícil de evitar."

Problemas de integração

A função gama encontra aplicação em áreas tão diversas como física quântica, astrofísica e dinâmica de fluidos. A distribuição gama, que é formulada em termos da função gama, é usada em estatística para modelar uma ampla gama de processos; por exemplo, o tempo entre ocorrências de terremotos.

A principal razão para a utilidade da função gama em tais contextos é a prevalência de expressões do tipo ${displaystyle f(t)e^{-g(t)}}$ que descreve processos que decaem exponencialmente no tempo ou no espaço. As integrais de tais expressões podem ocasionalmente ser resolvidas em termos da função gama quando nenhuma solução elementar existe. Por exemplo, se $f$ é uma função de energia e $g$ é uma função linear, uma simples mudança de variáveis ${displaystyle u:=acdot t}$ dá a avaliação

{displaystyle int _{0}^{infty }t^{b}e^{-at},dt={frac {1}{a^{b}}}int _{0}^{infty }u^{b}e^{-u}dleft({frac {u}{a}}right)={frac {Gamma (b+1)}{a^{b+1}}}.}

O fato de a integração ser realizada ao longo de toda a linha real positiva pode significar que a função gama descreve a acumulação de um processo dependente do tempo que continua indefinidamente, ou o valor pode ser o total de uma distribuição em um espaço infinito.

É claro que é frequentemente útil tomar limites de integração diferentes de 0 e $\infty$ para descrever a acumulação de um processo finito, caso em que a função gama comum não é mais uma solução; a solução é chamada de função gama incompleta. (A função gama comum, obtida pela integração em toda a linha real positiva, às vezes é chamada de função gama completa para contraste.)

Uma importante categoria de funções de decaimento exponencial é a das funções Gaussianas

{displaystyle ae^{-{frac {(x-b)^{2}}{c^{2}}}}}

{sqrt {pi }}

{textstyle Gamma left({frac {1}{2}}right)}

As integrais que discutimos até agora envolvem funções transcendentais, mas a função gama também surge de integrais de funções puramente algébricas. Em particular, os comprimentos de arco das elipses e da lemniscata, que são curvas definidas por equações algébricas, são dados por integrais elípticas que, em casos especiais, podem ser avaliadas em função da função gama. A função gama também pode ser usada para calcular o "volume" e "área" de hiperesferas $n$ dimensionais.

Cálculo de produtos

A capacidade da função gama de generalizar produtos fatoriais leva imediatamente a aplicações em muitas áreas da matemática; em combinatória e, por extensão, em áreas como a teoria da probabilidade e o cálculo de séries de potência. Muitas expressões envolvendo produtos de inteiros sucessivos podem ser escritas como alguma combinação de fatoriais, sendo o exemplo mais importante talvez o do coeficiente binomial

{displaystyle {binom {n}{k}}={frac {n!}{k!(n-k)!}}.}

O exemplo dos coeficientes binomiais explica porque as propriedades da função gama quando estendidas a números negativos são naturais. Um coeficiente binomial fornece o número de maneiras de escolher $k$ elementos de um conjunto de $n$ elementos; se $k > n$ , é claro que não há maneiras. Se $k > n$ , $(n - k)!$ é o fatorial de um inteiro negativo e, portanto, infinito se usarmos a definição da função gama de fatoriais - a divisão pelo infinito fornece o valor esperado de 0.

Podemos substituir o fatorial por uma função gama para estender qualquer fórmula para os números complexos. Geralmente, isso funciona para qualquer produto em que cada fator é uma função racional da variável de índice, fatorando a função racional em expressões lineares. Se $P$ e $Q$ são polinômios mônicos de grau $m$ e $n$ com as respectivas raízes $p 1, \dots, p m$ e $q 1, \dots, q n$ , temos

{displaystyle prod _{i=a}^{b}{frac {P(i)}{Q(i)}}=left(prod _{j=1}^{m}{frac {Gamma (b-p_{j}+1)}{Gamma (a-p_{j})}}right)left(prod _{k=1}^{n}{frac {Gamma (a-q_{k})}{Gamma (b-q_{k}+1)}}right).}

Se tivermos uma maneira de calcular a função gama numericamente, é muito fácil calcular os valores numéricos de tais produtos. O número de funções gama no lado direito depende apenas do grau dos polinômios, portanto, não importa se $b - a$ é igual a 5 ou 10⁵. Tomando os limites apropriados, a equação também pode ser mantida mesmo quando o produto da esquerda contém zeros ou pólos.

Ao tomar limites, certos produtos racionais com infinitos fatores também podem ser avaliados em termos da função gama. Devido ao teorema da fatoração de Weierstrass, as funções analíticas podem ser escritas como produtos infinitos e, às vezes, podem ser representadas como produtos finitos ou quocientes da função gama. Já vimos um exemplo impressionante: a fórmula de reflexão representa essencialmente a função seno como o produto de duas funções gama. A partir desta fórmula, a função exponencial, bem como todas as funções trigonométricas e hiperbólicas, podem ser expressas em termos da função gama.

Mais funções ainda, incluindo a função hipergeométrica e seus casos especiais, podem ser representadas por meio de integrais de contorno complexas de produtos e quocientes da função gama, chamadas integrais de Mellin-Barnes.

Teoria analítica dos números

Uma aplicação da função gama é o estudo da função zeta de Riemann. Uma propriedade fundamental da função zeta de Riemann é sua equação funcional:

{displaystyle Gamma left({frac {s}{2}}right)zeta (s)pi ^{-{frac {s}{2}}}=Gamma left({frac {1-s}{2}}right)zeta (1-s)pi ^{-{frac {1-s}{2}}}.}

Entre outras coisas, isso fornece uma forma explícita para a continuação analítica da função zeta para uma função meromórfica no plano complexo e leva a uma prova imediata de que a função zeta tem infinitos chamados "trivial&# 34; zeros na reta real. Borwein et al. chama essa fórmula de "uma das mais belas descobertas da matemática". Outro candidato a esse título pode ser

{displaystyle zeta (s);Gamma (s)=int _{0}^{infty }{frac {t^{s}}{e^{t}-1}},{frac {dt}{t}}.}

Ambas as fórmulas foram derivadas por Bernhard Riemann em seu artigo seminal de 1859 "Ueber die Anzahl der Primzahlen unter einer gegebenen Größe" ("Sobre o número de primos menor que uma determinada magnitude"), um dos marcos no desenvolvimento da teoria analítica dos números - o ramo da matemática que estuda os números primos usando as ferramentas da análise matemática. Os números fatoriais, considerados como objetos discretos, são um conceito importante na teoria clássica dos números porque contêm muitos fatores primos, mas Riemann encontrou um uso para sua extensão contínua que, sem dúvida, acabou sendo ainda mais importante.

História

A função gama despertou o interesse de alguns dos matemáticos mais proeminentes de todos os tempos. Sua história, notavelmente documentada por Philip J. Davis em um artigo que lhe rendeu o Prêmio Chauvenet de 1963, reflete muitos dos principais desenvolvimentos da matemática desde o século XVIII. Nas palavras de Davis, "cada geração encontrou algo interessante a dizer sobre a função gama. Talvez a próxima geração também o faça."

Século XVIII: Euler e Stirling

Carta de Daniel Bernoulli a Christian Goldbach, 6 de outubro de 1729

O problema de estender o fatorial para argumentos não inteiros foi aparentemente considerado pela primeira vez por Daniel Bernoulli e Christian Goldbach na década de 1720. Em particular, em uma carta de Bernoulli para Goldbach datada de 6 de outubro de 1729, Bernoulli introduziu a representação do produto

{displaystyle x!=lim _{nto infty }left(n+1+{frac {x}{2}}right)^{x-1}prod _{k=1}^{n}{frac {k+1}{k+x}}}

x

Leonard Euler posteriormente deu duas definições diferentes: a primeira não era sua integral, mas um produto infinito bem definido para todos os números complexos $n$ outro do que os números inteiros negativos,

{displaystyle n!=prod _{k=1}^{infty }{frac {left(1+{frac {1}{k}}right)^{n}}{1+{frac {n}{k}}}},,}

do qual ele informou Goldbach em uma carta datada de 13 de outubro de 1729. Ele escreveu a Goldbach novamente em 8 de janeiro de 1730, para anunciar sua descoberta da representação integral

{displaystyle n!=int _{0}^{1}(-ln s)^{n},ds,,}

que é válido quando a parte real do número complexo $n$ é estritamente maior do que $- Sim.$ (i.e., $-1}" xmlns="http://www.w3.org/1998/Math/MathML">R R (n)>- Sim. - Sim. 1(n)>-1} -1}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/63b00e86e0fbd78addd3dee00c615021297fd77e" style="vertical-align: -0.838ex; width:11.197ex; height:2.843ex;"/>$ ). Pela mudança de variáveis $) = S$ , isso se torna a integral Euler familiar. Euler publicou seus resultados no artigo "De progressionibus transcendentibus seu quarum termini generales algebraice dari nequeunt" ("Sobre progressões transcendentais, isto é, aqueles cujos termos gerais não podem ser dados algebraicamente"), submetidos à Academia de São Petersburgo em 28 de novembro de 1729. Euler descobriu ainda algumas das propriedades funcionais importantes da função gama, incluindo a fórmula de reflexão.

James Stirling, um contemporâneo de Euler, também tentou encontrar uma expressão contínua para o fatorial e criou o que hoje é conhecido como fórmula de Stirling. Embora a fórmula de Stirling forneça uma boa estimativa de $n!$ , também para números não inteiros, ela não fornece o valor exato. Extensões de sua fórmula que corrigem o erro foram dadas pelo próprio Stirling e por Jacques Philippe Marie Binet.

Século XIX: Gauss, Weierstrass e Legendre

A primeira página do papel de Euler

Carl Friedrich Gauss reescreveu o produto de Euler como

{displaystyle Gamma (z)=lim _{mto infty }{frac {m^{z}m!}{z(z+1)(z+2)cdots (z+m)}}}

e usou esta fórmula para descobrir novas propriedades da função gama. Embora Euler tenha sido um pioneiro na teoria de variáveis complexas, ele não parece ter considerado o fatorial de um número complexo, como Gauss fez primeiro. Gauss também provou o teorema da multiplicação da função gama e investigou a conexão entre a função gama e as integrais elípticas.

Karl Weierstrass estabeleceu ainda mais o papel da função gama na análise complexa, começando com outra representação de produto,

{displaystyle Gamma (z)={frac {e^{-gamma z}}{z}}prod _{k=1}^{infty }left(1+{frac {z}{k}}right)^{-1}e^{frac {z}{k}},}

onde $γ$ é a constante de Euler–Mascheroni. Weierstrass originalmente escreveu seu produto como um para $1 / Γ$ , caso em que é assumido os zeros da função em vez de seus pólos. Inspirado por esse resultado, ele provou o que é conhecido como teorema da fatoração de Weierstrass — que qualquer função inteira pode ser escrita como um produto sobre seus zeros no plano complexo; uma generalização do teorema fundamental da álgebra.

O nome função gama e o símbolo $Γ$ foram introduzidos por Adrien-Marie Legendre por volta de 1811; Legendre também reescreveu a definição integral de Euler em sua forma moderna. Embora o símbolo seja um gama grego maiúsculo, não há um padrão aceito para definir se o nome da função deve ser escrito "função gama" ou "função Gama" (alguns autores simplesmente escrevem " $Γ$ -função"). A "função pi" notação $Π(z) = z!$ devido a Gauss às vezes é encontrada na literatura mais antiga, mas a de Legendre notação é dominante em obras modernas.

É justificado perguntar por que distinguir entre o "factorial comum" e a função gama usando símbolos distintos, e particularmente por que a função gama deve ser normalizada para $) n + 1) = n!$ em vez de simplesmente usar " $) n) = n!$ ". Considere que a notação para expoentes, $x n$ , foi generalizado de inteiros para números complexos $x zangão.$ sem nenhuma mudança. A motivação de Legendre para a normalização não parece ser conhecida, e tem sido criticada por alguns (o matemático do século XX, Cornelius Lanczos, por exemplo, o chamou de "válido de qualquer racionalidade" e usaria em vez disso $zangão.!$ ). A normalização de Legendre simplifica algumas fórmulas, mas complica outras. De um ponto de vista moderno, a normalização Legendre da função Gamma é a integral do caráter aditivo $e - Sim. x$ contra o caráter multiplicador $x zangão.$ com respeito à medida Haar ${textstyle {frac {dx}{x}}}$ sobre o grupo Lie $R +$ . Assim, esta normalização torna mais claro que a função gama é um análogo contínuo de uma soma de Gauss.

Séculos XIX-XX: caracterizando a função gama

É um tanto problemático que um grande número de definições tenha sido dado para a função gama. Embora descrevam a mesma função, não é totalmente simples provar a equivalência. Stirling nunca provou que sua fórmula estendida corresponde exatamente à função gama de Euler; uma prova foi dada pela primeira vez por Charles Hermite em 1900. Em vez de encontrar uma prova especializada para cada fórmula, seria desejável ter um método geral de identificação da função gama.

Uma maneira de provar seria encontrar uma equação diferencial que caracterize a função gama. A maioria das funções especiais em matemática aplicada surge como soluções para equações diferenciais, cujas soluções são únicas. No entanto, a função gama não parece satisfazer nenhuma equação diferencial simples. Otto Hölder provou em 1887 que a função gama pelo menos não satisfaz nenhuma equação diferencial algébrica, mostrando que uma solução para tal equação não poderia satisfazer a fórmula de recorrência da função gama, tornando-a uma função transcendentalmente transcendental. Este resultado é conhecido como teorema de Hölder.

Uma caracterização definitiva e geralmente aplicável da função gama não foi dada até 1922. Harald Bohr e Johannes Mollerup provaram então o que é conhecido como o teorema de Bohr–Mollerup: que a função gama é a única solução para a relação de recorrência fatorial que é positiva e logaritmicamente convexa para $z$ positivo e cujo valor é 1 é 1 (uma função é logaritmicamente convexa se seu logaritmo for convexo). Outra caracterização é dada pelo teorema de Wielandt.

O teorema de Bohr–Mollerup é útil porque é relativamente fácil provar a convexidade logarítmica para qualquer uma das diferentes fórmulas usadas para definir a função gama. Levando as coisas adiante, em vez de definir a função gama por qualquer fórmula específica, podemos escolher as condições do teorema de Bohr-Mollerup como definição e, em seguida, escolher qualquer fórmula que satisfaça as condições como ponto de partida para estudar a função gama.. Essa abordagem foi usada pelo grupo Bourbaki.

Borwein & Corless revisa três séculos de trabalho sobre a função gama.

Tabelas de referência e software

Embora a função gama possa ser calculada virtualmente tão facilmente quanto qualquer função matematicamente mais simples com um computador moderno - mesmo com uma calculadora de bolso programável - é claro que nem sempre foi esse o caso. Até meados do século 20, os matemáticos contavam com tabelas feitas à mão; no caso da função gama, notavelmente uma tabela calculada por Gauss em 1813 e outra calculada por Legendre em 1825.

Um gráfico desenhado à mão do valor absoluto da função gama complexa, de Tabelas de Funções Superiores por Jahnke e Emde[de].

Tabelas de valores complexos da função gama, bem como gráficos desenhados à mão, foram fornecidos em Tabelas de funções com fórmulas e curvas de Jahnke e Emde [de], publicado pela primeira vez na Alemanha em 1909. De acordo com Michael Berry, "a publicação em J&E de três gráfico dimensional mostrando os pólos da função gama no plano complexo adquiriu um status quase icônico."

Na verdade, havia pouca necessidade prática de qualquer coisa além dos valores reais da função gama até a década de 1930, quando aplicações para a função gama complexa foram descobertas na física teórica. À medida que os computadores eletrônicos se tornaram disponíveis para a produção de tabelas na década de 1950, várias tabelas extensas para a função gama complexa foram publicadas para atender à demanda, incluindo uma tabela com precisão de 12 casas decimais do National Bureau of Standards dos EUA.

reprodução de um enredo complexo famoso por Janhke e Emde (Tabelas de Funções com Fórmulas e Curvas, 4a ed., Dover, 1945) da função gama de -4.5-2.5i para 4.5+2.5i

Implementações de ponto flutuante de dupla precisão da função gama e seu logaritmo estão agora disponíveis na maioria dos softwares de computação científica e bibliotecas de funções especiais, por exemplo, TK Solver, Matlab, GNU Octave e GNU Scientific Library. A função gama também foi adicionada à biblioteca padrão C (math.h). Implementações de precisão arbitrária estão disponíveis na maioria dos sistemas de álgebra computacional, como Mathematica e Maple. PARI/GP, MPFR e MPFUN contêm implementações livres de precisão arbitrária. Em algumas calculadoras de software, por ex. Calculadora do Windows e Calculadora do GNOME, a função fatorial retorna Γ(x+1) quando a entrada x é um valor não inteiro.

Contenido relacionado

Más resultados...