Força de Coriolis

Na física, a força de Coriolis é uma força inercial ou fictícia que atua sobre objetos em movimento dentro de um referencial que gira em relação a um referencial inercial. Em um referencial com rotação no sentido horário, a força atua à esquerda do movimento do objeto. Em um com rotação no sentido anti-horário (ou anti-horário), a força atua para a direita. A deflexão de um objeto devido à força de Coriolis é chamada de efeito de Coriolis. Embora reconhecida anteriormente por outros, a expressão matemática para a força de Coriolis apareceu em um artigo de 1835 do cientista francês Gaspard-Gustave de Coriolis, em conexão com a teoria das rodas d'água. No início do século 20, o termo força de Coriolis começou a ser usado em conexão com a meteorologia.
As leis de movimento de Newton descrevem o movimento de um objeto em um referencial inercial (sem aceleração). Quando as leis de Newton são transformadas em um referencial rotativo, aparecem as acelerações de Coriolis e centrífugas. Quando aplicadas a objetos com massas, as respectivas forças são proporcionais às suas massas. A magnitude da força de Coriolis é proporcional à taxa de rotação, e a magnitude da força centrífuga é proporcional ao quadrado da taxa de rotação. A força de Coriolis atua em uma direção perpendicular a duas grandezas: a velocidade angular do referencial em rotação em relação ao referencial inercial e a velocidade do corpo em relação ao referencial em rotação, e sua magnitude é proporcional à velocidade do objeto em do referencial rotativo (mais precisamente, à componente de sua velocidade que é perpendicular ao eixo de rotação). A força centrífuga atua para fora na direção radial e é proporcional à distância do corpo do eixo da estrutura rotativa. Essas forças adicionais são denominadas forças inerciais, forças fictícias ou pseudoforças. Ao introduzir essas forças fictícias em um referencial rotativo, as leis do movimento de Newton podem ser aplicadas ao sistema rotativo como se fosse um sistema inercial; essas forças são fatores de correção que não são necessários em um sistema não rotativo.
No uso popular (não técnico) do termo "efeito Coriolis", o quadro de referência rotativo implícito é quase sempre a Terra. Como a Terra gira, os observadores terrestres precisam levar em conta a força de Coriolis para analisar corretamente o movimento dos objetos. A Terra completa uma rotação para cada ciclo dia/noite, portanto, para movimentos de objetos do cotidiano, a força de Coriolis é geralmente muito pequena comparada com outras forças; seus efeitos geralmente se tornam perceptíveis apenas para movimentos que ocorrem em grandes distâncias e longos períodos de tempo, como o movimento em grande escala do ar na atmosfera ou da água no oceano; ou onde a alta precisão é importante, como artilharia de longo alcance ou trajetórias de mísseis. Tais movimentos são limitados pela superfície da Terra, então apenas o componente horizontal da força de Coriolis é geralmente importante. Essa força faz com que os objetos em movimento na superfície da Terra sejam desviados para a direita (em relação à direção da viagem) no Hemisfério Norte e para a esquerda no Hemisfério Sul. O efeito de deflexão horizontal é maior perto dos pólos, uma vez que a taxa de rotação efetiva em torno de um eixo vertical local é maior ali e diminui para zero no equador. Ao invés de fluir diretamente de áreas de alta pressão para baixa pressão, como aconteceria em um sistema não rotativo, ventos e correntes tendem a fluir para a direita desta direção ao norte do equador (sentido anti-horário) e para a esquerda desta direção ao sul. dele (sentido horário). Este efeito é responsável pela rotação e, portanto, pela formação de ciclones (ver efeitos de Coriolis em meteorologia).
Para uma explicação intuitiva da origem da força de Coriolis, considere um objeto, obrigado a seguir a superfície da Terra e movendo-se para o norte no Hemisfério Norte. Visto do espaço sideral, o objeto não parece ir para o norte, mas tem um movimento para o leste (ele gira para a direita junto com a superfície da Terra). Quanto mais ao norte ele viaja, menor o "raio de seu paralelo (latitude)" (a distância mínima do ponto da superfície ao eixo de rotação, que está em um plano ortogonal ao eixo), e assim mais lento o movimento para o leste de sua superfície. À medida que o objeto se move para o norte, para latitudes mais altas, ele tende a manter a velocidade para o leste com a qual começou (em vez de desacelerar para corresponder à velocidade reduzida para o leste de objetos locais na superfície da Terra), então ele vira para o leste (ou seja, à direita de seu movimento inicial).
Embora não seja óbvio neste exemplo, que considera o movimento para o norte, a deflexão horizontal ocorre igualmente para objetos que se movem para o leste ou para o oeste (ou em qualquer outra direção). No entanto, a teoria de que o efeito determina a rotação da água de drenagem em uma banheira, pia ou vaso sanitário de tamanho típico foi repetidamente refutada por cientistas modernos; a força é insignificante comparada com as muitas outras influências na rotação.
História

O cientista italiano Giovanni Battista Riccioli e seu assistente Francesco Maria Grimaldi descreveram o efeito em conexão com a artilharia no Almagestum Novum de 1651, escrevendo que a rotação da Terra deveria fazer com que uma bala de canhão disparada para o norte desviasse para o leste. Em 1674, Claude François Milliet Dechales descreveu em seu Cursus seu Mundus Mathematicus como a rotação da Terra deveria causar uma deflexão nas trajetórias tanto de corpos em queda quanto de projéteis apontados para um dos planetas. pólos. Riccioli, Grimaldi e Dechales descreveram o efeito como parte de um argumento contra o sistema heliocêntrico de Copérnico. Em outras palavras, eles argumentaram que a rotação da Terra deveria criar o efeito e, portanto, a falha em detectar o efeito era evidência de uma Terra imóvel. A equação de aceleração de Coriolis foi derivada por Euler em 1749, e o efeito foi descrito nas equações de maré de Pierre-Simon Laplace em 1778.
Gaspard-Gustave Coriolis publicou um artigo em 1835 sobre o rendimento energético de máquinas com peças rotativas, como rodas d'água. Esse artigo considerou as forças suplementares que são detectadas em um referencial rotativo. Coriolis dividiu essas forças suplementares em duas categorias. A segunda categoria continha uma força que surge do produto vetorial da velocidade angular de um sistema de coordenadas e a projeção da velocidade de uma partícula em um plano perpendicular ao eixo de rotação do sistema. Coriolis referiu-se a esta força como a "força centrífuga composta" devido às suas analogias com a força centrífuga já considerada na categoria um. O efeito era conhecido no início do século 20 como a "aceleração de Coriolis", e em 1920 como "força de Coriolis".
Em 1856, William Ferrel propôs a existência de uma célula de circulação nas latitudes médias com o ar sendo desviado pela força de Coriolis para criar os ventos predominantes de oeste.
A compreensão da cinemática de como exatamente a rotação da Terra afeta o fluxo de ar foi parcial no início. No final do século 19, a extensão total da interação em larga escala da força gradiente de pressão e da força de deflexão que, no final, faz com que as massas de ar se movam ao longo de isóbaras foi compreendida.
Fórmula
Na mecânica newtoniana, a equação de movimento para um objeto em um referencial inercial é
- F= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =mum{displaystyle {boldsymbol {F}}=m{boldsymbol {a}}}
Onde? F- Sim. é a soma vetorial das forças físicas que atuam no objeto, mNão. é a massa do objeto, e um- Sim. é a aceleração do objeto em relação ao quadro de referência inercial.
Transformando esta equação em um quadro de referência girando sobre um eixo fixo através da origem com velocidade angular ω ω O que é isso?) com taxa de rotação variável, a equação toma o formulário
- F?= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =F- Sim. - Sim. mDω ω D)× × R?- Sim. - Sim. 2mω ω × × v?- Sim. - Sim. mω ω × × (ω ω × × R?)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =mum?{displaystyle {begin{aligned}{boldsymbol {F'}}&={boldsymbol {F}}-m{frac Não. - Sim. }}}{mathrm {d} t}}times {boldsymbol (r) 2m - Sim. {v'}}-m{boldsymbol {omega }}times ({boldsymbol {omega }}times {boldsymbol {r'}})&=m{boldsymbol {a'}}end{aligned}}}
onde
- F- Sim. é a soma vetorial das forças físicas que atuam no objeto
- ω ω O que é isso?) é a velocidade angular, do quadro de referência rotativo em relação ao quadro inercial
- R?- Sim. é o vetor de posição do objeto em relação ao quadro de referência rotativo
- v?(v'}} é a velocidade do objeto em relação ao quadro de referência rotativo
- um?- Sim. é a aceleração do objeto em relação ao quadro de referência rotativo
As forças fictícias, conforme são percebidas no quadro rotativo, atuam como forças adicionais que contribuem para a aceleração aparente, assim como as forças externas reais. Os termos de força fictícia da equação são, lendo da esquerda para a direita:
- Força Euler, - Sim. - Sim. mDω ω D)× × R?Não. - Sim. - Sim. }}}{mathrm {d} t}}times {boldsymbol {r'}}}
- Força Coriolis, - Sim. - Sim. 2m(ω ω × × v?){displaystyle -2m({boldsymbol {omega }}times {boldsymbol {v'}}}
- força centrífuga, - Sim. - Sim. mω ω × × (ω ω × × R?)Não. -m{boldsymbol {omega }}times ({boldsymbol {omega }}times {boldsymbol {r'}})}
Observe que as forças Euler e centrífugas dependem do vetor de posição R?- Sim. do objeto, enquanto a força Coriolis depende da velocidade do objeto v?(v'}} como medida no quadro de referência rotativo. Como esperado, para um quadro inercial não rotativo de referência (ω ω = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0)(em inglês) a força Coriolis e todas as outras forças fictícias desaparecem. As forças também desaparecem para a massa zero (m= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =0)(m=0)}.
Como a força de Coriolis é proporcional a um produto vetorial de dois vetores, ela é perpendicular a ambos os vetores, neste caso a velocidade do objeto e o vetor de rotação do referencial. Segue-se, portanto, que:
- se a velocidade for paralela ao eixo de rotação, a força Coriolis é zero. Por exemplo, na Terra, essa situação ocorre para um corpo no equador que se move para norte ou sul em relação à superfície da Terra.
- se a velocidade estiver diretamente para o eixo, a força Coriolis está na direção da rotação local. Por exemplo, na Terra, esta situação ocorre para um corpo no equador caindo para baixo, como na ilustração Dechales acima, onde a bola cai mais para o leste do que a torre.
- se a velocidade for diretamente para fora do eixo, a força Coriolis é contra a direção da rotação local. No exemplo da torre, uma bola lançada para cima se moveria para o oeste.
- se a velocidade estiver na direção da rotação, a força Coriolis está para fora do eixo. Por exemplo, na Terra, essa situação ocorre para um corpo no equador que se move para o leste em relação à superfície da Terra. Ele se moveria para cima como visto por um observador na superfície. Este efeito (ver Eötvös efeito abaixo) foi discutido por Galileu Galilei em 1632 e por Riccioli em 1651.
- se a velocidade for contra a direção da rotação, a força Coriolis é para o eixo. Por exemplo, na Terra, essa situação ocorre para um corpo no equador que se move para o oeste, o que desvia para baixo como visto por um observador.
Escalas de comprimento e o número de Rossby
As escalas de tempo, espaço e velocidade são importantes para determinar a importância da força Coriolis. Se a rotação é importante em um sistema pode ser determinada pelo seu número Rossby, que é a relação da velocidade, U, de um sistema ao produto do parâmetro Coriolis, f= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2ω ω pecado φ φ {displaystyle f=2omega sin varphi ,}, e a escala de comprimento, L, da moção:
- Ro= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =UfL.Não. Ro... {U}{fL}}.}
O número de Rossby é a razão entre as forças inerciais e de Coriolis. Um pequeno número de Rossby indica que um sistema é fortemente afetado pelas forças de Coriolis, e um grande número de Rossby indica um sistema no qual as forças inerciais dominam. Por exemplo, em tornados, o número de Rossby é grande, em sistemas de baixa pressão é baixo e em sistemas oceânicos é de cerca de 1. Como resultado, em tornados a força de Coriolis é insignificante e o equilíbrio é entre pressão e forças centrífugas. Em sistemas de baixa pressão, a força centrífuga é desprezível e o equilíbrio ocorre entre Coriolis e as forças de pressão. Nos oceanos, todas as três forças são comparáveis.
Um sistema atmosférico movendo-se a U = 10 m/s (22 mph) ocupando uma distância espacial de L = 1.000 km (621 mi), tem um número de Rossby de aproximadamente 0,1.
Um arremessador de beisebol pode lançar a bola a U = 45 m/s (100 mph) por uma distância de L = 18,3 m (60 ft). O número de Rossby neste caso seria 32.000 (na latitude 31°47'46.382").
Os jogadores de beisebol não se importam com o hemisfério em que estão jogando. No entanto, um míssil não guiado obedece exatamente à mesma física de um beisebol, mas pode viajar longe o suficiente e ficar no ar por tempo suficiente para experimentar o efeito da força de Coriolis. Os projéteis de longo alcance no Hemisfério Norte caíram perto, mas à direita, de onde foram apontados até que isso fosse notado. (Aqueles disparados no Hemisfério Sul pousaram à esquerda.) Na verdade, foi esse efeito que primeiro chamou a atenção do próprio Coriolis.
Casos simples
Bola lançada em um carrossel giratório
A figura ilustra uma bola lançada a partir das 12:00 horas em direção ao centro de um carrossel girando no sentido anti-horário. À esquerda, a bola é vista por um observador estacionário acima do carrossel, e a bola viaja em linha reta até o centro, enquanto o lançador gira no sentido anti-horário com o carrossel. À direita, a bola é vista por um observador girando com o carrossel, de modo que o arremessador parece estar às 12 horas. A figura mostra como a trajetória da bola vista pelo observador em rotação pode ser construída.
À esquerda, duas setas localizam a bola em relação ao lançador. Uma dessas setas vai do arremessador até o centro do carrossel (fornecendo a linha de visão do arremessador) e a outra aponta do centro do carrossel até a bola. (Esta seta fica mais curta à medida que a bola se aproxima do centro.) Uma versão deslocada das duas setas é mostrada pontilhada.
À direita é mostrado este mesmo par pontilhado de setas, mas agora o par está rigidamente girado para que a seta correspondente à linha de visão do lançador de bola em direção ao centro do carrossel esteja alinhada com 12:00 o&# 39;relógio. A outra seta do par localiza a bola em relação ao centro do carrossel, fornecendo a posição da bola vista pelo observador em rotação. Seguindo este procedimento para várias posições, a trajetória no referencial rotativo é estabelecida conforme mostrado pelo caminho curvo no painel direito.
A bola viaja no ar e não há força resultante sobre ela. Para o observador estacionário, a bola segue uma trajetória em linha reta, portanto não há problema em enquadrar essa trajetória com força líquida zero. No entanto, o observador em rotação vê um caminho curvo. A cinemática insiste que uma força (empurrando para a direita da direção instantânea de viagem para uma rotação anti-horária) deve estar presente para causar essa curvatura, então o observador em rotação é forçado a invocar uma combinação de forças centrífugas e de Coriolis para fornecer a força líquida necessária para causar a trajetória curva.
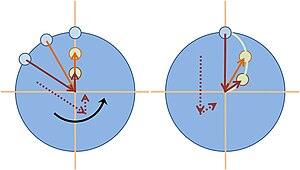
Bola quicada

A figura descreve uma situação mais complexa em que a bola lançada em uma plataforma giratória quica na borda do carrossel e então retorna para o lançador, que pega a bola. O efeito da força de Coriolis em sua trajetória é mostrado novamente como visto por dois observadores: um observador (referido como a "câmera") que gira com o carrossel e um observador inercial. A figura mostra uma visão panorâmica com base na mesma velocidade da bola nos caminhos de avanço e retorno. Dentro de cada círculo, os pontos traçados mostram os mesmos pontos de tempo. No painel esquerdo, do ponto de vista da câmera no centro de rotação, o arremessador (sorriso) e o trilho estão ambos em locais fixos, e a bola faz um arco considerável em sua viagem em direção ao trilho, e faz uma rota mais direta no caminho de volta. Do ponto de vista do arremessador, a bola parece retornar mais rapidamente do que foi (porque o arremessador está girando em direção à bola no voo de retorno).
No carrossel, em vez de jogar a bola diretamente em um trilho para ricochetear, o lançador deve jogar a bola para a direita do alvo e a bola parece para a câmera se mover continuamente para a esquerda de sua direção de viajar para atingir o trilho (esquerda porque o carrossel está girando no sentido horário). A bola parece estar voltada para a esquerda da direção de deslocamento nas trajetórias de ida e volta. O caminho curvo exige que esse observador reconheça uma força líquida para a esquerda na bola. (Esta força é "fictícia" porque desaparece para um observador estacionário, como será discutido em breve.) Para alguns ângulos de lançamento, um caminho tem porções onde a trajetória é aproximadamente radial, e a força de Coriolis é a principal responsável por a deflexão aparente da bola (a força centrífuga é radial a partir do centro de rotação e causa pouca deflexão nesses segmentos). Quando um caminho se afasta do radial, no entanto, a força centrífuga contribui significativamente para a deflexão.
O caminho da bola no ar é reto quando visto por observadores em pé no chão (painel direito). No painel direito (observador estacionário), o arremessador da bola (sorriso) está às 12 horas e a grade de onde a bola salta está na posição 1. Do ponto de vista do observador inercial, posições 1, 2, e 3 são ocupados em sequência. Na posição 2, a bola atinge a grade e na posição 3, a bola retorna ao arremessador. Caminhos em linha reta são seguidos porque a bola está em vôo livre, então esse observador requer que nenhuma força resultante seja aplicada.
Aplicado à Terra
A aceleração que afeta o movimento do ar "deslizamento" sobre a superfície da Terra é a componente horizontal do termo de Coriolis
- - Sim. - Sim. 2Ω Ω × × v{displaystyle -2,{boldsymbol - Sim.
Esta componente é ortogonal à velocidade sobre a superfície da Terra e é dada pela expressão
- ω ω v2pecado φ φ {displaystyle omega ,v 2,sin phi }
onde
- ω ω - Sim. é a taxa de rotação da Terra
- φ φ - Sim. é a latitude, positivo no hemisfério norte e negativo no hemisfério sul
No Hemisfério Norte, onde o sinal é positivo, esta força/aceleração, vista de cima, está à direita da direção do movimento, no Hemisfério Sul, onde o sinal é negativo, esta força/aceleração está à esquerda de a direção do movimento
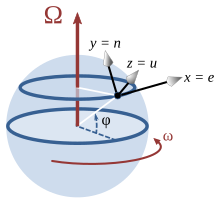
Esfera rotativa
Considere um local com latitude φ em uma esfera que está girando em torno do eixo norte-sul. Um sistema de coordenadas local é configurado com o eixo x horizontalmente para o leste, o eixo y horizontalmente para o norte e o eixo z verticalmente para cima. O vetor de rotação, velocidade de movimento e aceleração de Coriolis expressos neste sistema de coordenadas local (listando componentes na ordem leste (e), norte (n) e para cima (u)) são:
- Ω Ω = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =ω ω (0e φ φ pecado φ φ ),- Não. - Sim. {begin{pmatrix}0\cos varphi \\sin varphi end{pmatrix}}} v= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(vevnvu),- Não. {v}}={begin{pmatrix}v_{e}\v_{n}\v_{u}end{pmatrix}}}
- umC= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. 2Ω Ω × × v= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2ω ω (vnpecado φ φ - Sim. - Sim. vue φ φ - Sim. - Sim. vepecado φ φ vee φ φ ).- Não. {a}}_{C}=-2{boldsymbol {Omega times v}}=2,omega ,{begin{pmatrix}v_{n}sin varphi -v_{u}cos varphi \-v_{e}sin varphi \v_{e}cos varphi{pmatrix}}.}
Ao considerar a dinâmica atmosférica ou oceânica, a velocidade vertical é pequena e o componente vertical da aceleração Coriolis (vee φ φ Não. v_{e}cos varphi }) é pequeno comparado com a aceleração devido à gravidade (g, aproximadamente 9,81 m/s2 (32.2 ft/s)2) perto da superfície da Terra). Para tais casos, apenas os componentes horizontais (leste e norte) importam. A restrição do acima para o plano horizontal é (configuração vu= 0):
- v= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(vevn),- Não. {v}}={begin{pmatrix}v_{e}\v_{n}end{pmatrix}}} umc= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(vn- Sim. - Sim. ve)f,- Não. {a}}_{c}={begin{pmatrix}v_{n}\-v_{e}end{pmatrix}} Não.
Onde? f= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2ω ω pecado φ φ {displaystyle f=2omega sin varphi ,} é chamado de parâmetro Coriolis.
Ao definir vn = 0, pode-se ver imediatamente que (para φ e ω positivos) um movimento para leste resulta em uma aceleração para sul. Da mesma forma, configurando ve = 0, vê-se que um movimento para o norte resulta em uma aceleração para o leste.
Em geral, observada horizontalmente, olhando ao longo da direção do movimento que causa a aceleração, a aceleração sempre é virada 90° para a direita (para φ positivo) e do mesmo tamanho independentemente da orientação horizontal.
Como um caso diferente, considere a configuração do movimento equatorial φ = 0°. Neste caso, Ω é paralelo ao norte ou eixo n, e:
- Ω Ω = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =ω ω (010),- Não. - Sim. {displaystyle }01\0end{pmatrix}}} v= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =(vevnvu),- Não. {v}}={begin{pmatrix}v_{e}\v_{n}\v_{u}end{pmatrix}}} umC= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. 2Ω Ω × × v= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2ω ω (- Sim. - Sim. vu0ve).- Não. {a}}_{C}=-2{boldsymbol {Omega times v}}=2,omega ,{begin{pmatrix}-v_{u}\0v_{e}end{pmatrix}}.}
Conseqüentemente, um movimento para leste (ou seja, na mesma direção da rotação da esfera) fornece uma aceleração para cima conhecida como efeito Eötvös, e um movimento para cima produz uma aceleração para oeste.
Meteorologia e oceanografia

Talvez o impacto mais importante do efeito Coriolis esteja na dinâmica em larga escala dos oceanos e da atmosfera. Em meteorologia e oceanografia, é conveniente postular um referencial rotativo em que a Terra está estacionária. Em acomodação a essa postulação provisória, são introduzidas as forças centrífuga e de Coriolis. Sua importância relativa é determinada pelos números de Rossby aplicáveis. Os tornados têm altos números de Rossby, portanto, enquanto as forças centrífugas associadas aos tornados são bastante substanciais, as forças de Coriolis associadas aos tornados são, para fins práticos, insignificantes.
Como as correntes oceânicas superficiais são impulsionadas pelo movimento do vento sobre a superfície da água, a força de Coriolis também afeta o movimento das correntes oceânicas e dos ciclones. Muitas das maiores correntes oceânicas circulam em torno de áreas quentes e de alta pressão chamadas giros. Embora a circulação não seja tão significativa quanto a do ar, a deflexão causada pelo efeito Coriolis é o que cria o padrão espiral nesses giros. O padrão de vento em espiral ajuda a formar o furacão. Quanto mais forte a força do efeito Coriolis, mais rápido o vento gira e capta energia adicional, aumentando a força do furacão.
O ar dentro de sistemas de alta pressão gira em uma direção tal que a força de Coriolis é direcionada radialmente para dentro e quase equilibrada pelo gradiente de pressão radial para fora. Como resultado, o ar viaja no sentido horário em torno da alta pressão no Hemisfério Norte e no sentido anti-horário no Hemisfério Sul. O ar em torno de baixa pressão gira na direção oposta, de modo que a força de Coriolis é direcionada radialmente para fora e quase equilibra um gradiente de pressão radial para dentro.
Fluxo em torno de uma área de baixa pressão
Se uma área de baixa pressão se forma na atmosfera, o ar tende a fluir em sua direção, mas é desviado perpendicularmente à sua velocidade pela força de Coriolis. Um sistema de equilíbrio pode então se estabelecer criando um movimento circular, ou um fluxo ciclônico. Como o número de Rossby é baixo, o equilíbrio de força é em grande parte entre a força do gradiente de pressão atuando em direção à área de baixa pressão e a força de Coriolis atuando longe do centro de baixa pressão.
Em vez de fluir pelo gradiente, movimentos de grande escala na atmosfera e no oceano tendem a ocorrer perpendicularmente ao gradiente de pressão. Isso é conhecido como fluxo geostrófico. Em um planeta sem rotação, o fluido fluiria ao longo da linha mais reta possível, eliminando rapidamente os gradientes de pressão. O balanço geostrófico é, portanto, muito diferente do caso dos "movimentos inerciais" (veja abaixo), o que explica por que os ciclones de latitude média são maiores em uma ordem de magnitude do que o fluxo do círculo inercial seria.
Esse padrão de deflexão e a direção do movimento são chamados de lei de Buys-Ballot. Na atmosfera, o padrão de fluxo é chamado de ciclone. No Hemisfério Norte, a direção do movimento em torno de uma área de baixa pressão é anti-horária. No Hemisfério Sul, a direção do movimento é no sentido horário porque a dinâmica rotacional é uma imagem espelhada ali. Em grandes altitudes, o ar que se espalha para fora gira na direção oposta. Os ciclones raramente se formam ao longo do equador devido ao fraco efeito Coriolis presente nesta região.
Círculos inerciais
Uma massa de ar ou água que se move com velocidade vNão. sujeito apenas à força Coriolis viaja em uma trajetória circular chamada círculo inercial. Uma vez que a força é direcionada para ângulos retos ao movimento da partícula, ela se move com uma velocidade constante em torno de um círculo cujo raio RNão. R. é dado por:
- R= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =vfNão. Não.
Onde? fNão. é o parâmetro Coriolis 2Ω Ω pecado φ φ Não. 2Omega sin varphi }, introduzido acima (onde) φ φ - Sim. é a latitude). O tempo levado para a massa para completar um círculo completo é, portanto, 2D D /f{displaystyle 2pi /f}. O parâmetro Coriolis normalmente tem um valor de latitude média de cerca de 10-4S- Sim.; portanto, para uma velocidade atmosférica típica de 10 m/s (22 mph), o raio é de 100 km (62 mi) com um período de cerca de 17 horas. Para uma corrente oceânica com uma velocidade típica de 10 cm/s (0,22 mph), o raio de um círculo inercial é de 1 km (0,6 mi). Estes círculos inerciais são no sentido horário no hemisfério norte (onde as trajetórias são dobradas à direita) e anti-horário no hemisfério sul.
Se o sistema rotativo é um giratório parabólico, então fNão. é constante e as trajetórias são círculos exatos. Num planeta rotativo, fNão. varia com a latitude e os caminhos das partículas não formam círculos exatos. Desde o parâmetro fNão. varia conforme o seio da latitude, o raio das oscilações associadas a uma determinada velocidade são menores nos pólos (latitude de ±90°), e aumentam em direção ao equador.
Outros efeitos terrestres
O efeito Coriolis afeta fortemente a circulação oceânica e atmosférica em larga escala, levando à formação de feições robustas como correntes de jato e correntes de fronteira oeste. Tais feições estão em equilíbrio geostrófico, o que significa que as forças de Coriolis e gradiente de pressão se equilibram. A aceleração de Coriolis também é responsável pela propagação de muitos tipos de ondas no oceano e na atmosfera, incluindo ondas de Rossby e ondas de Kelvin. Também é instrumental na chamada dinâmica de Ekman no oceano e no estabelecimento do padrão de fluxo oceânico em larga escala chamado equilíbrio de Sverdrup.
Efeito Eötvös
O impacto prático do "efeito Coriolis" é causada principalmente pelo componente de aceleração horizontal produzido pelo movimento horizontal.
Existem outros componentes do efeito Coriolis. Objetos que viajam para o oeste são desviados para baixo, enquanto objetos que viajam para o leste são desviados para cima. Isso é conhecido como efeito Eötvös. Este aspecto do efeito Coriolis é maior perto do equador. A força produzida pelo efeito Eötvös é semelhante à componente horizontal, mas as forças verticais muito maiores devido à gravidade e à pressão sugerem que ela não é importante no equilíbrio hidrostático. No entanto, na atmosfera, os ventos estão associados a pequenos desvios de pressão do equilíbrio hidrostático. Na atmosfera tropical, a ordem de grandeza dos desvios de pressão é tão pequena que a contribuição do efeito Eötvös para os desvios de pressão é considerável.
Além disso, objetos viajando para cima (ou seja, para fora) ou para baixo (ou seja, para dentro) são desviados para oeste ou leste, respectivamente. Este efeito também é maior perto do equador. Como o movimento vertical é geralmente de extensão e duração limitadas, o tamanho do efeito é menor e requer instrumentos precisos para detectar. Por exemplo, estudos de modelagem numérica idealizados sugerem que esse efeito pode afetar diretamente o campo de vento tropical em grande escala em cerca de 10%, devido ao aquecimento ou resfriamento de longa duração (2 semanas ou mais) na atmosfera. Além disso, no caso de grandes mudanças de momento, como uma espaçonave sendo lançada em órbita, o efeito torna-se significativo. O caminho mais rápido e mais econômico para a órbita é um lançamento do equador que se curva diretamente para o leste.
Exemplo intuitivo
Imagine um trem que viaja através de uma linha ferroviária sem atrito ao longo do equador. Assuma que, quando em movimento, ele se move na velocidade necessária para completar uma viagem ao redor do mundo em um dia (465 m/s). O efeito Coriolis pode ser considerado em três casos: quando o trem viaja para o oeste, quando está em repouso, e quando viaja para o leste. Em cada caso, o efeito Coriolis pode ser calculado a partir do quadro rotativo de referência na Terra primeiro, e depois verificado contra um quadro inercial fixo. A imagem abaixo ilustra os três casos vistos por um observador em repouso em um quadro inercial (perto) de um ponto fixo acima do Pólo Norte ao longo do eixo de rotação da Terra; o trem é denotado por alguns pixels vermelhos, fixados no lado esquerdo na imagem mais esquerda, movendo-se nos outros (1dia= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =∧ ∧ 8S):{displaystyle left(1{text{ day}}mathrel {overset {land }{=}} 8{text{ s}}right):}
- O trem viaja para o oeste: Nesse caso, ele se move contra a direção da rotação. Portanto, no quadro rotativo da Terra, o termo Coriolis é apontado para dentro para o eixo de rotação (para baixo). Esta força adicional para baixo deve fazer com que o trem seja mais pesado enquanto se move nessa direção.Se alguém olhar para este trem do quadro fixo não-rotating em cima do centro da Terra, a essa velocidade permanece estacionária à medida que a Terra gira abaixo dela. Assim, a única força que atua nela é a gravidade e a reação da pista. Esta força é maior (de 0,34%) do que a força que os passageiros e a experiência de trem quando em repouso (rotando junto com a Terra). Esta diferença é o que o efeito Coriolis representa no quadro rotativo de referência.
- O comboio chega a uma paragem: Do ponto de vista no quadro rotativo da Terra, a velocidade do trem é zero, assim a força Coriolis também é zero e o trem e seus passageiros recuperam seu peso habitual.Do quadro inercial fixo de referência acima da Terra, o trem agora gira junto com o resto da Terra. 0,34% da força da gravidade fornece a força centrípeta necessária para alcançar o movimento circular nesse quadro de referência. A força restante, medida por uma escala, torna o trem e os passageiros "mais leves" do que no caso anterior.
- O comboio viaja para leste. Neste caso, porque se move na direção do quadro rotativo da Terra, o termo Coriolis é direcionado para fora do eixo de rotação (up). Esta força ascendente faz o trem parecer mais leve do que quando em repouso.Do quadro inercial fixo de referência acima da Terra, o trem que viaja para leste agora gira ao dobro da taxa como quando estava em repouso - então a quantidade de força centrípeta necessária para causar que o caminho circular aumenta deixando menos força da gravidade para agir na pista. Este é o que o termo Coriolis conta no parágrafo anterior.Como uma verificação final pode-se imaginar um quadro de referência girando junto com o trem. Tal quadro seria girando duas vezes a velocidade angular como o quadro rotativo da Terra. O componente de força centrífuga resultante para esse quadro imaginário seria maior. Como o trem e seus passageiros estão em repouso, esse seria o único componente nesse quadro explicando novamente por que o trem e os passageiros são mais leves do que nos dois casos anteriores.
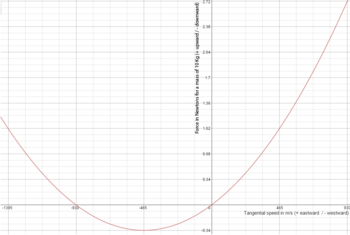 Gráfico da força experimentada por um objeto de 10 quilogramas (22 lb) como uma função de sua velocidade que se move ao longo do equador da Terra (como medido dentro do quadro rotativo). (A força positiva no gráfico é direcionada para cima. A velocidade positiva é direcionada para o leste e a velocidade negativa é direcionada para o oeste).
Gráfico da força experimentada por um objeto de 10 quilogramas (22 lb) como uma função de sua velocidade que se move ao longo do equador da Terra (como medido dentro do quadro rotativo). (A força positiva no gráfico é direcionada para cima. A velocidade positiva é direcionada para o leste e a velocidade negativa é direcionada para o oeste).
Isso também explica por que projéteis de alta velocidade que viajam para o oeste são desviados para baixo e aqueles que viajam para o leste são desviados para cima. Essa componente vertical do efeito Coriolis é chamada de efeito Eötvös.
O exemplo acima pode ser usado para explicar por que o efeito Eötvös começa a diminuir quando um objeto está viajando para o oeste à medida que sua velocidade tangencial aumenta acima da rotação da Terra (465 m/s). Se o trem para o oeste no exemplo acima aumentar a velocidade, parte da força da gravidade que empurra os trilhos é responsável pela força centrípeta necessária para mantê-lo em movimento circular no referencial inercial. Uma vez que o trem dobra sua velocidade para o oeste a 930 m/s (2.100 mph), essa força centrípeta torna-se igual à força que o trem experimenta quando para. A partir do referencial inercial, em ambos os casos, ele gira na mesma velocidade, mas em direções opostas. Assim, a força é a mesma cancelando completamente o efeito Eötvös. Qualquer objeto que se mova para o oeste a uma velocidade acima de 930 m/s (2.100 mph) experimenta uma força ascendente. Na figura, o efeito Eötvös é ilustrado para um objeto de 10 kg (22 lb) no trem em diferentes velocidades. A forma parabólica é porque a força centrípeta é proporcional ao quadrado da velocidade tangencial. No referencial inercial, a base da parábola está centrada na origem. O deslocamento ocorre porque esse argumento usa o quadro de referência rotativo da Terra. O gráfico mostra que o efeito Eötvös não é simétrico e que a força descendente resultante experimentada por um objeto que viaja para o oeste em alta velocidade é menor do que a força ascendente resultante quando ele viaja para o leste na mesma velocidade.
Esvaziamento em banheiras e vasos sanitários
Ao contrário do equívoco popular, banheiras, vasos sanitários e outros recipientes de água não drenam em direções opostas nos hemisférios norte e sul. Isso ocorre porque a magnitude da força de Coriolis é desprezível nessa escala. As forças determinadas pelas condições iniciais da água (por exemplo, a geometria do dreno, a geometria do receptáculo, o momento preexistente da água etc.) de rotação da água, se houver. Por exemplo, vasos sanitários idênticos com descarga em ambos os hemisférios drenam na mesma direção, e essa direção é determinada principalmente pelo formato do vaso sanitário.
Sob condições do mundo real, a força de Coriolis não influencia perceptivelmente a direção do fluxo de água. Somente se a água estiver tão parada que a taxa de rotação efetiva da Terra seja mais rápida do que a da água em relação ao seu recipiente e se os torques aplicados externamente (como os que podem ser causados pelo fluxo sobre uma superfície de fundo irregular) forem pequenos o suficiente, o efeito Coriolis pode de fato determinar a direção do vórtice. Sem essa preparação cuidadosa, o efeito Coriolis será muito menor do que várias outras influências na direção do dreno, como qualquer rotação residual da água e a geometria do recipiente.
Ensaios laboratoriais de drenagem de água em condições atípicas
Em 1962, Ascher Shapiro realizou um experimento no MIT para testar a força de Coriolis em uma grande bacia de água, 2 metros (6 ft 7 in) de largura, com uma pequena cruz de madeira acima do orifício do bujão para exibir a direção da rotação, cobrindo-o e esperando pelo menos 24 horas para que a água assente. Sob essas condições laboratoriais precisas, ele demonstrou o efeito e a rotação anti-horária consistente.
Ele relatou que,
Ambas as escolas de pensamento estão em certo sentido. Para as observações diárias da cozinha pia e variedade de banheira, a direção do vórtice parece variar de forma imprevisível com a data, a hora do dia, e a casa particular do experimentador. Mas sob condições bem controladas de experimentação, o observador olhando para baixo em um dreno no hemisfério norte sempre verá um vórtice anti-horário, enquanto um no hemisfério sul sempre verá um vórtice no sentido horário. Em uma experiência adequadamente projetada, o vórtice é produzido pelas forças Coriolis, que são anti-horário no hemisfério norte.
Lloyd Trefethen relatou a rotação no sentido horário no Hemisfério Sul na Universidade de Sydney em cinco testes com tempos de estabilização de 18 horas ou mais.
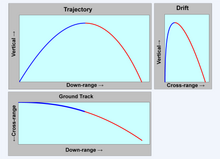
Trajetórias balísticas
A força de Coriolis é importante em balística externa para calcular as trajetórias de projéteis de artilharia de longo alcance. O exemplo histórico mais famoso foi o canhão de Paris, usado pelos alemães durante a Primeira Guerra Mundial para bombardear Paris a uma distância de cerca de 120 km (75 mi). A força de Coriolis altera minuciosamente a trajetória de uma bala, afetando a precisão em distâncias extremamente longas. É ajustado por atiradores precisos de longa distância, como atiradores de elite. Na latitude de Sacramento, Califórnia, um tiro de 1.000 yd (910 m) para o norte seria desviado 2,8 in (71 mm) para a direita. Há também um componente vertical, explicado na seção do efeito Eötvös acima, que faz com que os tiros para o oeste sejam baixos e os tiros para o leste sejam altos.
Os efeitos da força de Coriolis em trajetórias balísticas não devem ser confundidos com a curvatura dos caminhos de mísseis, satélites e objetos semelhantes quando os caminhos são traçados em mapas bidimensionais (planos), como a projeção de Mercator. As projeções da superfície curva tridimensional da Terra para uma superfície bidimensional (o mapa) resultam necessariamente em feições distorcidas. A curvatura aparente do caminho é consequência da esfericidade da Terra e ocorreria mesmo em um referencial sem rotação.
A força de Coriolis em um projétil em movimento depende dos componentes da velocidade em todas as três direções, latitude e azimute. As direções são tipicamente downrange (a direção que a arma está apontando inicialmente), vertical e cross-range.
- AX= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =- Sim. - Sim. 2ω ω (VYe θ θ Eu...um)pecado φ φ umzangão.+VZ.pecado θ θ Eu...um))(Exibido A_{mathrm {X} }=-2omega (V_{mathrm {Y} }cos theta _{mathrm {lat} }sin phi _{mathrm {az} }+V_{mathrm {Z} }sin theta _{mathrm {lat} }
- AY= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2ω ω (VXe θ θ Eu...um)pecado φ φ umzangão.+VZ.e θ θ Eu...um)e φ φ umzangão.)(Exibido A_{mathrm {Y} }=2omega (V_{mathrm {X} }cos theta _{mathrm {lat} }sin phi _{mathrm {az} }+V_{mathrm {Z} }cos theta _{mathrm {lat} }cos phi _{mathrm {az} })}
- AZ.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =2ω ω (VXpecado θ θ Eu...um)- Sim. - Sim. VYe θ θ Eu...um)e φ φ umzangão.)(Exibido A_{mathrm {Z} }=2omega (V_{mathrm {X} }sin theta _{mathrm {lat} ? {Y} }cos theta _{mathrm {lat} }cos phi _{mathrm {az} })}
onde
- AX(Exibido A_{mathrm (X)Aceleração para baixo.
- AY{displaystyle A_{mathrm {Y} }}, aceleração vertical com aceleração indicativa positiva para cima.
- AZ.(Exibido A_{mathrm (Z), aceleração cross-range com aceleração positiva indicando à direita.
- VX- Sim. (X)Velocidade de down-range.
- VY{displaystyle V_{mathrm {Y} }}, velocidade vertical com indicação positiva para cima.
- VZ.- Sim. (Z), velocidade de cross-range com velocidade de indicação positiva para a direita.
- ω ω - Sim. = 0,00007292 rad/sec, velocidade angular da terra (baseada em um dia sideral).
- θ θ Eu...um){displaystyle theta _{mathrm {lat} }}, latitude com indicação positiva do hemisfério norte.
- φ φ umzangão.{displaystyle phi _{mathrm {az} }}, azimute mediu no sentido horário do norte devido.
Visualização do efeito Coriolis
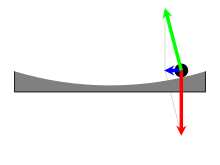
Para demonstrar o efeito Coriolis, uma plataforma giratória parabólica pode ser usada. Em uma plataforma giratória plana, a inércia de um objeto em co-rotação o força para fora da borda. No entanto, se a superfície da plataforma giratória tiver a forma correta de paraboloide (recipiente parabólico) (veja a figura) e girar na taxa correspondente, os componentes da força mostrados na figura tornam o componente da gravidade tangencial à superfície do recipiente exatamente igual à força centrípeta necessário para manter o objeto girando em sua velocidade e raio de curvatura (supondo que não haja atrito). (Consulte curva inclinada.) Essa superfície cuidadosamente contornada permite que a força de Coriolis seja exibida isoladamente.
Discos cortados de cilindros de gelo seco podem ser usados como discos, movendo-se quase sem atrito sobre a superfície da plataforma giratória parabólica, permitindo que os efeitos de Coriolis em fenômenos dinâmicos se mostrem. Para obter uma visão dos movimentos vistos a partir do quadro de referência girando com a plataforma giratória, uma câmera de vídeo é acoplada à plataforma giratória para co-rotar com a plataforma giratória, com resultados conforme mostrado na figura. No painel esquerdo da figura, que é o ponto de vista de um observador estacionário, a força gravitacional no referencial inercial puxando o objeto em direção ao centro (parte inferior) do prato é proporcional à distância do objeto ao centro. Uma força centrípeta desta forma causa o movimento elíptico. No painel direito, que mostra o ponto de vista do referencial rotativo, a força gravitacional interna no referencial rotativo (a mesma força que no referencial inercial) é equilibrada pela força centrífuga externa (presente apenas no referencial rotativo). Com essas duas forças equilibradas, no referencial rotativo a única força desequilibrada é Coriolis (também presente apenas no referencial rotativo), e o movimento é um círculo inercial. A análise e observação do movimento circular no referencial rotativo é uma simplificação em comparação com a análise e observação do movimento elíptico no referencial inercial.
Como esse referencial gira várias vezes por minuto, em vez de apenas uma vez por dia, como a Terra, a aceleração de Coriolis produzida é muitas vezes maior e mais fácil de observar em pequenas escalas de tempo e espaço do que a aceleração de Coriolis causada pela rotação da Terra.
Por assim dizer, a Terra é análoga a tal plataforma giratória. A rotação fez com que o planeta assumisse uma forma esferóide, de modo que a força normal, a força gravitacional e a força centrífuga se equilibrassem exatamente em uma posição "horizontal" superfície. (Ver protuberância equatorial.)
O efeito Coriolis causado pela rotação da Terra pode ser visto indiretamente através do movimento de um pêndulo de Foucault.
Efeitos Coriolis em outras áreas
Medidor de vazão Coriolis
Uma aplicação prática do efeito Coriolis é o medidor de fluxo de massa, um instrumento que mede a taxa de fluxo de massa e a densidade de um fluido que flui através de um tubo. O princípio de funcionamento envolve induzir uma vibração do tubo através do qual o fluido passa. A vibração, embora não completamente circular, fornece o referencial giratório que dá origem ao efeito Coriolis. Embora os métodos específicos variem de acordo com o projeto do medidor de vazão, os sensores monitoram e analisam as mudanças na frequência, mudança de fase e amplitude dos tubos de fluxo vibrantes. As mudanças observadas representam a vazão mássica e a densidade do fluido.
Física molecular
Em moléculas poliatômicas, o movimento da molécula pode ser descrito por uma rotação de corpo rígido e vibração interna de átomos em torno de sua posição de equilíbrio. Como resultado das vibrações dos átomos, os átomos estão em movimento em relação ao sistema de coordenadas rotativas da molécula. Os efeitos de Coriolis estão, portanto, presentes e fazem os átomos se moverem em uma direção perpendicular às oscilações originais. Isso leva a uma mistura no espectro molecular entre os níveis rotacional e vibracional, a partir dos quais as constantes de acoplamento de Coriolis podem ser determinadas.
Precessão giroscópica
Quando um torque externo é aplicado a um giroscópio giratório ao longo de um eixo que está em ângulo reto com o eixo de rotação, a velocidade do aro associada ao giro torna-se radialmente direcionada em relação ao eixo de torque externo. Isso faz com que uma força induzida por torque atue no aro de forma a inclinar o giroscópio em ângulos retos na direção em que o torque externo o teria inclinado. Essa tendência tem o efeito de manter os corpos girando em seu referencial rotacional.
Vôo de insetos
Moscas (Diptera) e algumas mariposas (Lepidoptera) exploram o efeito Coriolis em vôo com apêndices e órgãos especializados que transmitem informações sobre a velocidade angular de seus corpos.
As forças de Coriolis resultantes do movimento linear desses apêndices são detectadas dentro do referencial rotativo dos insetos. corpos. No caso das moscas, seus apêndices especializados são órgãos em forma de halteres localizados logo atrás de suas asas chamados de "halteres".
Os halteres da mosca oscilam em um plano na mesma frequência de batimento das asas principais, de modo que qualquer rotação do corpo resulta em desvio lateral dos halteres de seu plano de movimento.
Nas mariposas, sabe-se que suas antenas são responsáveis pela sensação das forças de Coriolis de maneira semelhante aos halteres das moscas. Tanto em moscas quanto em mariposas, uma coleção de mecanossensores na base do apêndice é sensível a desvios na frequência de batimento, correlacionando-se com a rotação nos planos de inclinação e rotação, e no dobro da frequência de batimento, correlacionando-se com a rotação no plano de guinada.
Estabilidade do ponto Lagrangeano
Na astronomia, os pontos lagrangianos são cinco posições no plano orbital de dois grandes corpos em órbita, onde um pequeno objeto afetado apenas pela gravidade pode manter uma posição estável em relação aos dois grandes corpos. Os primeiros três pontos lagrangeanos (L1, L2, L3) encontram-se ao longo da linha que liga os dois grandes corpos, enquanto os dois últimos pontos (L4 e L5) cada um forma um triângulo equilátero com os dois grandes corpos. Os pontos L4 e L5, embora correspondam a máximos do potencial efetivo no referencial de coordenadas que gira com os dois grandes corpos, são estáveis devido ao efeito Coriolis. A estabilidade pode resultar em órbitas em torno de apenas L4 ou L5, conhecidas como órbitas de girinos, onde troianos podem ser encontrados. Também pode resultar em órbitas que circundam L3, L4 e L5, conhecidas como órbitas em ferradura.
Contenido relacionado
Experimento de fenda dupla
Processo adiabático
Fahrenheit