Fatorial

Fatores selecionados; valores na notação científica são arredondados

$Não.$	$Não!$
0	1
1	1
2	2
3	6
4	24.
5	120
6	720
7	5040
8	40320
9	362880
10.	3628800
11	39916800
12	479001600
13	6227020800
14	87178291200
15	1307674368)
16.	20.92789888)
17.	355687428096)
18.	6402373705728)
19	121645100.408832)
20.	2432902008176640)
25	1.551121004×10.25
50	3.041409320×10.64
70	1.197857167×10.100.
100.	9.332621544×10.157
450	1.733368733×10.1)
1)	4.023872601×10.2567
3249	6.412337688×10.10.)
10.)	2.846259681×10.35659
25206	1.205703438×10.100.)
100.)	2.824229408×10.456573
205023	2.503898932×10.1)004
1))	8.263931688×10.5565708
10100	10.10.101.9981097754820

Em matemática, o factorial de um não negativo Intérprete $Não.$, denotado por $Não!$, é o produto de todos os inteiros positivos menos ou igual para $Não.$. O factorial de $Não.$ também é igual ao produto de $Não.$ com o factorial menor seguinte:

$${displaystyle {begin{aligned}n!&=ntimes (n-1)times (n-2)times (n-3)times cdots times 3times 2times 1&=ntimes (n-1)! \end{aligned}}}$$

$${displaystyle 5!=5times 4!=5times 4times 3times 2times 1=120.}$$

Os fatores foram descobertos em várias culturas antigas, notadamente na matemática indiana nas obras canônicas da literatura Jain, e por místicos judeus no livro Talmudic Sefer Yetzirah. A operação fatorial é encontrada em muitas áreas da matemática, notavelmente em combinatória, onde seu uso mais básico conta as possíveis sequências distintas – as permutações – de $Não.$ objetos distintos: lá são $Não!$ Na análise matemática, os fatores são usados em séries de poder para a função exponencial e outras funções, e eles também têm aplicações em álgebra, teoria dos números, teoria da probabilidade e ciência da computação.

Grande parte da matemática da função fatorial foi desenvolvida a partir do final do século 18 e início do século 19. A aproximação de Stirling fornece uma aproximação precisa para o fatorial de grandes números, mostrando que ele cresce mais rapidamente do que o crescimento exponencial. A fórmula de Legendre descreve os expoentes dos números primos em uma fatoração prima dos fatoriais e pode ser usada para contar os zeros à direita dos fatoriais. Daniel Bernoulli e Leonhard Euler interpolaram a função fatorial para uma função contínua de números complexos, exceto nos inteiros negativos, a função gama (offset).

Muitas outras funções notáveis e sequências numéricas estão intimamente relacionadas aos fatoriais, incluindo os coeficientes binomiais, fatoriais duplos, fatoriais decrescentes, primoriais e subfatoriais. As implementações da função fatorial são comumente usadas como exemplo de diferentes estilos de programação de computadores e estão incluídas em calculadoras científicas e bibliotecas de software de computação científica. Embora o cálculo direto de grandes fatoriais usando a fórmula do produto ou recorrência não seja eficiente, algoritmos mais rápidos são conhecidos, combinando dentro de um fator constante o tempo para algoritmos de multiplicação rápida para números com o mesmo número de dígitos.

História

O conceito de fatoriais surgiu de forma independente em muitas culturas:

• Em matemática indiana, uma das primeiras descrições conhecidas de fatores vem do Anuyogadvāra-sūtra, uma das obras canônicas da literatura Jain, que foi atribuída datas variando de 300 a.C. a 400 d.C. Ele separa a ordem ordenada e revertida de um conjunto de itens de outras ordens ("misturadas"), avaliando o número de ordens mistas subtraindo duas da fórmula de produto habitual para o fatorial. A regra do produto para permutações também foi descrita pelo CE Jain monk Jinabhadra do século VI. Os estudiosos hindus têm usado fórmulas fatoriais desde pelo menos 1150, quando Bhāskara II mencionou fatores em seu trabalho Līlāvatī, em conexão com um problema de quantas maneiras Vishnu poderia segurar seus quatro objetos característicos (uma concha de conch, disco, mace e flor de lótus) em suas quatro mãos, e um problema semelhante para um deus de dez mãos.
• Na matemática do Oriente Médio, o livro místico hebraico da criação Sefer Yetzirah, do período talmúdico (200 a 500 CE), lista os fatores até 7! como parte de uma investigação sobre o número de palavras que podem ser formadas do alfabeto hebraico. Os fatores também foram estudados por razões semelhantes pelo gramático árabe Al-Khalil ibn Amade al-Farahidi. O matemático árabe Ibn al-Haytham (também conhecido como Alhazen, c. 965 - c. 1040) foi o primeiro a formular o teorema de Wilson conectando os fatores com os números primos.
• Na Europa, embora a matemática grega incluísse alguns combinatórios, e Platão usou famosamente 5.040 (um fatorial) como a população de uma comunidade ideal, em parte por causa de suas propriedades de divisibilidade, não há nenhuma evidência direta do estudo grego antigo de fatores. Em vez disso, o primeiro trabalho sobre fatores na Europa foi por estudiosos judeus como Shabbethai Donnolo, explicando a passagem Sefer Yetzirah. Em 1677, o autor britânico Fabian Stedman descreveu a aplicação de fatores para mudar o toque, uma arte musical envolvendo o toque de vários sinos sintonizados.

A partir do final do século XV, os fatores tornaram-se objeto de estudo por matemáticos ocidentais. Em um tratado de 1494, o matemático italiano Luca Pacioli calculou fatores até 11!, em conexão com um problema de arranjos de mesa de jantar. Christopher Clavius discutiu fatores em um comentário de 1603 sobre o trabalho de Johannes de Sacrobosco, e na década de 1640, o polimate francês Marin Mersenne publicou grandes (mas não inteiramente corretos) tabelas de fatores, até 64!, com base no trabalho de Clavius. A série de potência para a função exponencial, com os recíprocos de fatores para seus coeficientes, foi primeiramente formulada em 1676 por Isaac Newton em uma carta a Gottfried Wilhelm Leibniz. Outras obras importantes de matemática europeia precoce sobre fatores incluem ampla cobertura em um tratado de 1685 por John Wallis, um estudo de seus valores aproximados para grandes valores de $Não.$ por Abraham de Moivre em 1721, uma carta de 1729 de James Stirling para de Moivre afirmando o que se tornou conhecido como aproximação de Stirling, e trabalhar ao mesmo tempo por Daniel Bernoulli e Leonhard Euler formulando a extensão contínua da função fatorial para a função gama. Adrien-Marie Legendre incluiu a fórmula de Legendre, descrevendo os expoentes na fatoração de fatores em poderes primos, em um texto de 1808 sobre teoria dos números.

A notação $Não!$ para fatores foi introduzido pelo matemático francês Christian Kramp em 1808. Muitas outras notações também foram usadas. Outra notação posterior, em que o argumento do fatorial foi meio fechado pelos lados esquerdo e inferior de uma caixa, foi popular por algum tempo na Grã-Bretanha e América, mas caiu fora de uso, talvez porque é difícil de digitar. A palavra "fatorial" (originalmente francês: Facilitador) foi usado pela primeira vez em 1800 por Louis François Antoine Arbogast, no primeiro trabalho sobre a fórmula de Faà di Bruno, mas referindo-se a um conceito mais geral de produtos de progressões aritméticas. Os "factores" que este nome refere são os termos da fórmula do produto para o fatorial.

Definição

A função fatorial de um inteiro positivo $Não.$ é definido pelo produto de todos os inteiros positivos não maiores do que $Não.$

$${displaystyle n!=1cdot 2cdot 3cdots (n-2)cdot (n-1)cdot n.}$$

$$_{i=1}^{n}i.}$$

Se esta fórmula do produto for alterada para manter tudo menos o último termo, ela definiria um produto da mesma forma, para um fatorial menor. Isso leva a uma relação de recorrência, segundo a qual cada valor da função fatorial pode ser obtido multiplicando o valor anterior por $Não.$:

$$(n-1)!.}$$

$5!=5cdot 4!=5cdot 24=120}$.

Fatorial de zero

O factorial de $Não. 0$ o $Não. 1$, ou em símbolos, $Não.$. Existem várias motivações para esta definição:

• Para $Não.$, a definição de $Não!$ como um produto envolve o produto de nenhum número, e assim é um exemplo da convenção mais ampla que o produto vazio, um produto de nenhum fator, é igual à identidade multiplicativa.
• Há exatamente uma permutação de zero objetos: sem nada a permutar, o único rearranjo é não fazer nada.
• Esta convenção torna muitas identidades em combinatória válidas para todas as escolhas válidas de seus parâmetros. Por exemplo, o número de maneiras de escolher todos $Não.$ elementos de um conjunto de $Não.$ o $- Sim. Não. Não!$ uma identidade de coeficiente binomial que só seria válida com $Não.$.
• Com $Não.$, a relação de recorrência para o fatorial permanece válida em $Não.$. Portanto, com esta convenção, uma computação recursiva do fatorial precisa ter apenas o valor para zero como um caso base, simplificando a computação e evitando a necessidade de casos especiais adicionais.
• Configuração $Não.$ permite a expressão compacta de muitas fórmulas, como a função exponencial, como uma série de energia: $- Sim. _{n=0}^{infty }{frac {x^{n}}{n!}}.}$
• Esta escolha corresponde à função gama $0!=Gamma (0+1)=1}$, e a função gama deve ter esse valor para ser uma função contínua.

Aplicativos

Os primeiros usos da função fatorial envolvem a contagem de permutações: há $Não!$ maneiras diferentes de organizar $Não.$ objetos distintos em uma sequência. Os fatores aparecem mais amplamente em muitas fórmulas em combinatória, para explicar diferentes pedidos de objetos. Por exemplo, os coeficientes binomiais $Não.$ contar $Não.$- Elemento combinações (subconjuntos de $Não.$ elementos) de um conjunto com $Não.$ elementos, e pode ser computado de fatores usando a fórmula

$${displaystyle {binom {n}{k}}={frac Não!$$

de $Não.$

$Não.$

para $Não. Não!$.

Na álgebra, os fatoriais surgem através do teorema binomial, que usa coeficientes binomiais para expandir potências de somas. Eles também ocorrem nos coeficientes usados para relacionar certas famílias de polinômios entre si, por exemplo, nas identidades de Newton para polinômios simétricos. Seu uso na contagem de permutações também pode ser reapresentado algebricamente: os fatoriais são as ordens de grupos simétricos finitos. No cálculo, os fatoriais ocorrem na fórmula de Faà di Bruno para encadear derivadas superiores. Na análise matemática, os fatoriais freqüentemente aparecem nos denominadores das séries de potências, principalmente nas séries da função exponencial,

$$Não. e^{x=1+ (x){1}+ {x^{2}}{2}}+{frac {x^{3}}{6}}+cdots =sum _{i=0}^{infty }{frac {x^{i}}{i!}},}$$

$Não!$

$Não.$derivado de

de ${displaystyle x^{n}}$.

$Não. N_{i}}$

tamanho $Não.$

$${displaystyle sum _{i=0}^{infty }{frac {x^{i}n_{i}}{i!}}}}$$

Na teoria dos números, a propriedade mais saliente dos fatores é a divisibilidade $Não!$ por todos os inteiros positivos para $Não.$, descrito mais precisamente para os principais fatores pela fórmula de Legendre. Segue-se que arbitrariamente grandes números primos podem ser encontrados como os principais fatores dos números $Não! 1$, levando a uma prova do teorema de Euclides que o número de primos é infinito. Quando $Não! 1$ é em si próprio primo chama-se um primo factorial; afinadamente, problema de Brocard, também posado por Srinivasa Ramanujan, diz respeito à existência de números quadrados da forma $- Sim.$. Em contraste, os números $Não!$ todos devem ser compostos, provando a existência de grandes lacunas arbitrárias. Uma prova elementar do postulado de Bertrand sobre a existência de um primo em qualquer intervalo do formulário $Não.$, um dos primeiros resultados de Paul Erdős, foi baseado nas propriedades de divisibilidade dos fatores. O sistema de número fatoral é uma notação de radix mista para números em que os valores de lugar de cada dígito são fatores.

Os fatores são usados extensivamente na teoria da probabilidade, por exemplo na distribuição de Poisson e nas probabilidades de permutações aleatórias. Na ciência da computação, além de aparecer na análise de pesquisas de força bruta sobre permutações, os fatores surgem no limite inferior de ${displaystyle log _{2}n!=nlog _{2}n-O(n)}$ no número de comparações necessárias para comparar um conjunto de $Não.$ itens, e na análise de tabelas de hash em cadeia, onde a distribuição de chaves por célula pode ser exatamente aproximada por uma distribuição de Poisson. Além disso, os fatores aparecem naturalmente em fórmulas da física quântica e estatística, onde muitas vezes se considera todas as possíveis permutações de um conjunto de partículas. Na mecânica estatística, cálculos de entropia como a fórmula de entropia de Boltzmann ou a equação de Sackur-Tetrode devem corrigir a contagem de microestados dividindo-se pelos fatores dos números de cada tipo de partícula indistinguível para evitar o paradoxo de Gibbs. A física quântica fornece a razão subjacente para por que essas correções são necessárias.

Propriedades

Crescimento e aproximação

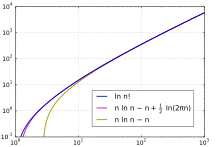
Comparação do factorial, aproximação de Stirling e aproximação mais simples $(n/e)^{n}}$, em uma escala duplamente logarítmica

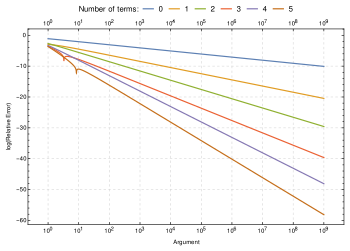
Erro relativo em uma série de Stirling truncado vs. número de termos

Como uma função de $Não.$, o fatorial tem mais rápido do que o crescimento exponencial, mas cresce mais lentamente do que uma função exponencial dupla. Sua taxa de crescimento é semelhante para ${displaystyle n^{n}}$, mas mais lento por um fator exponencial. Uma maneira de abordar este resultado é tomando o logaritmo natural do fatorial, que transforma sua fórmula de produto em uma soma, e depois estimando a soma por uma integral:

$${displaystyle ln n!=sum _{x=1}^{n}ln xapprox int _{1}^{n}ln x,dx=nln n n n-n+1.}$$

$Não. +1$

$Não!$

$(n/e)^{n}}$.

para $- Sim.$.

$- Sim.$

$${displaystyle n!sim {sqrt {2pi n}}left({frac {n}{e}}right)^{n},.}$$

$- Sim.$

$Não.$

$${displaystyle n!sim {sqrt {2pi n}}left({frac {n}{e}}right)^{n}left(1+{frac {1}{12n}+{frac {1}{288n^{2}}}-{frac {139}{51840n^{3}}}-{frac {571}{2488320n^{4}}}+cdots right).}$$

$${displaystyle n!sim {sqrt {2pi n}}left({frac {n}{e}}right)^{n}exp left({frac {1}{12n} {1}{360n^{3}}}+{frac {1}{1260n^{5}}}-{frac {1}{1680n^{7}}}+cdots right).}$$

O logaritmo binário do fatorial, usado para analisar a classificação de comparação, pode ser muito exatamente estimado usando a aproximação de Stirling. Na fórmula abaixo, o $Não.$ termo invoca grande notação O.

$${displaystyle log} _{2}n!=nlog _{2}n-(log _{2}e)n+{frac {1}{2}}log _{2}n+O(1).}$$

Divisibilidade e dígitos

A fórmula do produto para o fatorial implica que $Não!$ é divisível por todos os números primos que estão em mais $Não.$, e sem números primos maiores. Mais informações precisas sobre sua divisibilidade é dada pela fórmula de Legendre, que dá o expoente de cada primo $Não.$ na primeira fatoração de $Não!$ como

$${displaystyle sum _{i=1}^{infty }leftlfloor {frac {n}{p^{i}}}rightrfloor ={frac {n-s_{p}(n)}{p-1}}.}$$

$(n)}$

Base...$Não.$

de $Não.$,

O caso especial da fórmula de Legendre para $Não.$ dá o número de zeros rastreantes na representação decimal dos fatores. De acordo com esta fórmula, o número de zeros pode ser obtido subtraindo os dígitos base-5 de $Não.$ a partir de $Não.$, e dividindo o resultado por quatro. A fórmula de Legendre implica que o expoente do primeiro $Não.$ é sempre maior do que o expoente para $Não.$, assim cada fator de cinco pode ser emparelhado com um fator de dois para produzir um desses zeros rastreadores. Os dígitos principais dos fatores são distribuídos de acordo com a lei de Benford. Cada sequência de dígitos, em qualquer base, é a sequência de dígitos iniciais de algum número factorial nessa base.

Outro resultado na divisibilidade dos fatores, o teorema de Wilson, afirma que $(n-1)!+1}$ é divisível por $Não.$ se e somente se $Não.$ é um número primo. Para qualquer dado Intérprete $Não.$, a função de Kempner $Não.$ é dado pelo menor $Não.$ para os quais $Não.$ divide $Não!$. Para quase todos os números (todos menos um subconjunto de exceções com densidade assintótica zero), coincide com o maior fator principal de $Não.$.

O produto de dois fatores, $Não!$, sempre uniformemente divide $(m+n)!}$. Há infinitamente muitos fatores que igualam o produto de outros fatores: se $Não.$ é em si qualquer produto de fatores, então $Não!$ é igual ao mesmo produto multiplicado por mais um factorial, $(n-1)!}$. Os únicos exemplos conhecidos de fatores que são produtos de outros fatores, mas não são desta forma "trivial" são $[displaystyle 9!=7!cdot 3!cdot 3!cdot 2!}$, $10!=7!cdot 6!=7!cdot 5!cdot 3!}$, e $Não!$. Seguiria da conjectura abc que existem apenas exemplos finitos não triviais.

O maior divisor comum dos valores de um polinômio primitivo de grau $Não.$ sobre os inteiros uniformemente divide $Não!$.

Interpolação contínua e generalização não inteira

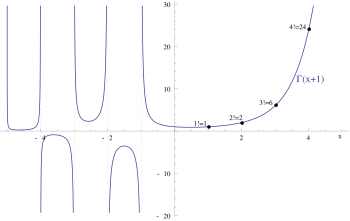
A função gama (muda uma unidade esquerda para corresponder aos fatores) interpola continuamente os valores factoriais aos valores não inteiros

Valores absolutos da função gama complexa, mostrando pólos em inteiros não positivos

Existem infinitas maneiras de estender os fatoriais para uma função contínua. O mais amplamente utilizado deles usa a função gama, que pode ser definida para números reais positivos como a integral

$$Não. Gamma (z)=int _{0}^{infty }x^{z-1}e^{-x},dx}$$

$Não.$

$$(n+1),}$$

$Não.$

$(x)}$

$(x-1)}$

$${displaystyle Gamma (n)=(n-1)Gamma (n-1),}$$

A mesma integral converge mais geralmente para qualquer número complexo $Não.$ cuja parte real é positiva. Pode ser estendido para os pontos não inteiros no resto do plano complexo resolvendo para a fórmula de reflexão de Euler

$${displaystyle Gamma (z)Gamma (1-z)={frac {pi }{sin pi z}}.}$$

${displaystyle sin pi z}$

Outras funções complexas que interpolam os valores fatoriais incluem a função gama de Hadamard, que é uma função inteira sobre todos os números complexos, incluindo os inteiros não positivos. Nos números p-ádicos, não é possível interpolar continuamente a função fatorial diretamente, porque os fatoriais de inteiros grandes (um subconjunto denso do p-adics) convergem para zero de acordo com a fórmula de Legendre, forçando qualquer função contínua que esteja próxima de seus valores a ser zero em todos os lugares. Em vez disso, a função gama p-ádica fornece uma interpolação contínua de uma forma modificada do fatorial, omitindo os fatores no fatorial que são divisíveis por p .

A função digamma é a derivada logarítmica da função gama. Assim como a função gama fornece uma interpolação contínua dos fatoriais, compensada por um, a função digamma fornece uma interpolação contínua dos números harmônicos, compensada pela constante de Euler-Mascheroni.

Computação

TI SR-50A, uma calculadora de 1975 com uma chave factorial (terceira linha, centro direito)

A função fatorial é uma característica comum em calculadoras científicas. Também está incluído em bibliotecas de programação científica, como o módulo de funções matemáticas Python e a biblioteca Boost C++. Se a eficiência não é uma preocupação, os fatores de computação é trivial: apenas sucessivamente multiplicar uma variável inicializada para $Não. 1$ pelos inteiros para $Não.$. A simplicidade desta computação torna um exemplo comum no uso de diferentes estilos e métodos de programação de computador.

A computação $Não!$ pode ser expresso em pseudocódigo usando iteração como

definir factorial(n:
 f? 1
para Eu...:= 1, 2, 3,..., n:
 f? f × Eu...retorno f

ou usando recursão com base em sua relação de recorrência como

definir factorial(n:
se n = 0 devolução 1
retorno n × factorial(n - 1)

Outros métodos adequados para sua computação incluem memoização, programação dinâmica e programação funcional. A complexidade computacional desses algoritmos pode ser analisada usando o modelo de computador de acesso aleatório de custo unitário, no qual cada operação aritmética leva tempo constante e cada número usa uma quantidade constante de espaço de armazenamento. Neste modelo, esses métodos podem computar $Não!$ em tempo $O(n)}$, e a versão iterativa usa espaço $Não.$. A menos que otimizado para recursão da cauda, a versão recursiva leva espaço linear para armazenar sua pilha de chamadas. No entanto, este modelo de computação só é adequado quando $Não.$ é pequeno o suficiente para permitir $Não!$ caber em uma palavra de máquina. Os valores 12! e 20! são os maiores fatores que podem ser armazenados em, respectivamente, os inteiros de 32 bits e 64 bits. O ponto flutuante pode representar fatores maiores, mas aproximadamente em vez de exatamente, e ainda irá transbordar para fatores maiores do que os fatores. $170!$.

A computação exata de fatores maiores envolve aritmética de precisão arbitrária, por causa do crescimento rápido e do fluxo inteiro. O tempo de computação pode ser analisado como uma função do número de dígitos ou bits no resultado. Pela fórmula de Stirling, $Não!$ ele tem $(nlog n)}$ bits. O algoritmo de Schönhage-Strassen pode produzir $Não.$- Adeus. produto em tempo $Não. O(blog blog log b)}$, e algoritmos de multiplicação mais rápidos levando tempo $(blog b)}$ são conhecidos. No entanto, a computação do fatorial envolve produtos repetidos, em vez de uma única multiplicação, de modo que esses limites de tempo não se aplicam diretamente. Nesta configuração, computação $Não!$ multiplicando os números de 1 para $Não.$ em sequência é ineficiente, porque envolve $Não.$ multiplicações, uma fração constante da qual levam tempo $(nlog ^{2}n)}$ cada, dando tempo total ${displaystyle O(n^{2}log ^{2}n)}$. Uma melhor abordagem é executar as multiplicações como um algoritmo de divisão e conquista que multiplica uma sequência de $Não.$ números dividindo-o em duas subsequências de $- Sim.$ números, multiplica cada subsequência, e combina os resultados com uma última multiplicação. Esta abordagem do factorial leva tempo total $(nlog ^{3}n)}$: um logaritmo vem do número de bits no fatorial, um segundo vem do algoritmo de multiplicação, e um terço vem da divisão e conquista.

Ainda melhor eficiência é obtida pela computação n! de sua fatoração principal, com base no princípio de que a exponencialização por squaring é mais rápida do que expandir um expoente em um produto. Um algoritmo para isso por Arnold Schönhage começa encontrando a lista dos primos para $Não.$, por exemplo, usando a peneira de Eratosthenes, e usa a fórmula de Legendre para calcular o expoente para cada primo. Em seguida, ele computa o produto dos poderes primos com esses expoentes, usando um algoritmo recursivo, como segue:

• Use dividir e conquistar para calcular o produto dos primos cujos expoentes são estranhos
• Dividir todos os expoentes por dois (arredondando para um inteiro), recursivamente computar o produto dos poderes primos com esses expoentes menores, e ajustar o resultado
• Multiplique os resultados das duas etapas anteriores

O produto de todos os primos até $Não.$ é um $O(n)}$-bit number, by theorem número primo, então o tempo para o primeiro passo é $(nlog ^{2}n)}$, com um logaritmo vindo da divisão e conquistar e outro vindo do algoritmo de multiplicação. Nas chamadas recursivas ao algoritmo, o teorema do número primo pode ser invocado novamente para provar que o número de bits nos produtos correspondentes diminui por um fator constante em cada nível de recursão, de modo que o tempo total para essas etapas em todos os níveis de recursão adiciona em uma série geométrica para $(nlog ^{2}n)}$. O tempo para a quadratura no segundo passo e a multiplicação no terceiro passo são novamente $(nlog ^{2}n)}$, porque cada um é uma única multiplicação de um número com $O(nlog n)}$ bits. Mais uma vez, em cada nível de recursão os números envolvidos têm uma fração constante como muitos bits (porque, de outra forma, repetidamente squaring eles produziriam um resultado final muito grande) então novamente as quantidades de tempo para essas etapas nas chamadas recursivas adicionam em uma série geométrica para $(nlog ^{2}n)}$. Consequencialmente, todo o algoritmo leva Tempo $(nlog ^{2}n)}$, proporcional a uma única multiplicação com o mesmo número de bits em seu resultado.

Sequências e funções relacionadas

Várias outras sequências inteiras são semelhantes ou relacionadas aos fatoriais:

Factorial alternativo

O factorial alternante é o valor absoluto da soma alternada do primeiro $Não.$ fatores, $- Sim. _{i=1}^{n}(-1)^{n-i}i!}$. Estes foram estudados principalmente em conexão com sua primalidade; apenas finitamente muitos deles podem ser primos, mas uma lista completa de primos desta forma não é conhecida.

Fatorial de Bhargava

Os fatores Bhargava são uma família de sequências de inteiros definidas por Manjul Bhargava com propriedades teóricas de números semelhantes aos fatores, incluindo os próprios fatores como um caso especial.

Dupla fatoração

O produto de todos os inteiros ímpares até algum positivo estranho Intérprete $Não.$ é chamado de fatoração dupla de $Não.$, e denotado por $Não!$. Isso é,

$${displaystyle (2k-1)!!=prod _{i=1}^{k}(2i-1)={frac {(2k)! }{2^{k}k!}}.}$$

Por exemplo, 9!! = 1 × 3 × 5 × 7 × 9 = 945. Os fatores duplos são usados em integrais trigonométricas, em expressões para a função gama em meio inteiros e os volumes de hipersferas, e na contagem de árvores binárias e combinações perfeitas.

Fatorial experiencial

Assim como números triangulares somam os números de $Não. 1$ para $Não.$, e os fatores tomam seu produto, o fatorial exponencial exponencial. O fatorial exponencial é definido recursivamente como ${displaystyle a_{0}=1, a_{n}=n^{a_{n-1}}}$. Por exemplo, o fatorial exponencial de 4 é

$$Não. 4^{3^{2^{1}}}=262144.}$$

Esses números crescem muito mais rapidamente do que os fatores regulares.

Fatorial de queda

As notações ${displaystyle (x)_{n}}$ ou ${displaystyle x^{sublinha Não.$ às vezes são usados para representar o produto do $Não.$ inteiros contando até e incluindo $Não.$, igual a $(x-n)!}$. Isso também é conhecido como fatorial de queda ou retrocesso, e o ${displaystyle (x)_{n}}$ notação é um símbolo Pochhammer. Fatoriais em queda contam o número de diferentes sequências de $Não.$ itens distintos que podem ser extraídos de um universo de $Não.$ itens. Eles ocorrem como coeficientes nos derivados mais elevados de polinômios e nos momentos fatorais de variáveis aleatórias.

Hiperfactoriais

O hiperfatorial de $Não.$ é o produto ${displaystyle 1^{1}cdot 2^{2}cdots n^{n}}$. Esses números formam os discriminantes de polinômios hermitas. Eles podem ser interpolados continuamente pela função K, e obedecer análogos à fórmula de Stirling e teorema de Wilson.

Números Jordan–Pólya

Os números Jordan-Pólya são os produtos dos fatores, permitindo repetições. Cada árvore tem um grupo de simetria cujo número de simetrias é um número Jordan-Pólya, e cada número Jordan-Pólya conta as simetrias de alguma árvore.

Primorial

O primorial $Não.$ é o produto de números primos inferior ou igual para $Não.$; esta construção dá-lhes algumas propriedades de divisibilidade semelhantes aos fatores, mas ao contrário dos fatores que são livres de quadrados. Como com os primos factoriais $Não! 1$, pesquisadores estudaram primos primorais ${displaystyle n#pm 1}$.

Subfactorial

O subfactorial produz o número de desconjuntos de um conjunto de $Não.$ objetos. Às vezes é denotado $Não.$, e é igual ao inteiro mais próximo para $Não. Não!$.

Superfatorial

O superfatorial de $Não.$ é o produto do primeiro $Não.$ Fatoriais. Os superfatoriais são continuamente interpolados pela função Barnes G.