Falácia do jogador
A falácia do jogador, também conhecida como falácia de Monte Carlo ou falácia da maturidade das chances, é a crença incorreta de que, se um determinado evento ocorre com mais frequência do que o normal durante o passado, é menos provável que aconteça no futuro (ou vice-versa), quando foi estabelecido de outra forma que a probabilidade de tais eventos não depende do que aconteceu aconteceu no passado. Tais eventos, tendo a qualidade de independência histórica, são referidos como estatisticamente independentes. A falácia é comumente associada ao jogo, onde pode-se acreditar, por exemplo, que a próxima jogada de dados provavelmente será seis, porque recentemente houve menos do que o número esperado de seis.
O termo "falácia de Monte Carlo" origina-se do exemplo mais conhecido do fenômeno, ocorrido no Cassino de Monte Carlo em 1913.
Exemplos
Jogo da moeda
A falácia do jogador pode ser ilustrada considerando o lançamento repetido de uma moeda honesta. Os resultados em diferentes lances são estatisticamente independentes e a probabilidade de obter cara em um único lance é 1/2 (um em dois). A probabilidade de obter duas caras em dois lançamentos é 1/4 (uma em quatro) e a probabilidade de obter três caras em três jogadas é 1/8 (um em oito). Em geral, se Ai é o evento em que o lançamento i de uma moeda honesta dá cara, então:
- Pr(⋂ ⋂ Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1nAEu...)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =? ? Eu...= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =1nPr(AEu...)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =12nNão. Pr left(bigcap _{i=1}^{n}A_{i}right)=prod _{i=1}^{n}Pr(A_{i})={1 over 2^{n}}}.
Se depois de jogar quatro caras seguidas, o próximo lançamento da moeda também desse cara, isso completaria uma sequência de cinco caras sucessivas. Como a probabilidade de uma sequência de cinco caras consecutivas é 1/32 (um em trinta e dois), uma pessoa pode acreditar que a próxima jogada seria mais provável de sair coroa em vez de cara novamente. Isso é incorreto e é um exemplo da falácia do jogador. O evento "5 cabeças consecutivas" e o evento "primeiras 4 caras, depois coroa" são igualmente prováveis, cada uma com probabilidade 1/32. Como os primeiros quatro lançamentos resultam em cara, a probabilidade de que o próximo lançamento seja cara é:
- Pr(A5|A1─ ─ A2─ ─ A3─ ─ A4)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =Pr(A5)= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =12Não. Pr left(A_{5}|A_{1}cap A_{2}cap A_{3}cap A_{4}right)=Pr left(A_{5}right)={frac Não..
Enquanto uma sequência de cinco caras tem uma probabilidade de 1 /32 = 0,03125 (pouco mais de 3%), o mal-entendido está em não perceber que esse é o caso apenas antes do primeiro a moeda é lançada. Após os primeiros quatro lançamentos neste exemplo, os resultados não são mais desconhecidos, então suas probabilidades são iguais a 1 (100%). A probabilidade de uma série de lançamentos de uma moeda de qualquer comprimento continuar por mais um lançamento é sempre 0,5. O raciocínio de que é mais provável que um quinto lançamento seja coroa porque os quatro lançamentos anteriores foram cara, com uma sequência de sorte no passado influenciando as probabilidades no futuro, forma a base da falácia.
Por que a probabilidade é 1/2 para uma moeda honesta
Se uma moeda honesta for lançada 21 vezes, a probabilidade de 21 caras é de 1 em 2.097.152. A probabilidade de tirar cara depois de já ter jogado 20 caras seguidas é 1/2. Supondo uma moeda honesta:
- A probabilidade de 20 cabeças, então 1 cauda é 0,520. × 0,5 = 0,521
- A probabilidade de 20 cabeças, então 1 cabeça é 0,520. × 0,5 = 0,521
A probabilidade de obter 20 caras e depois 1 coroa e a probabilidade de obter 20 caras e outra cara são ambas de 1 em 2.097.152. Ao jogar uma moeda honesta 21 vezes, o resultado tem a mesma probabilidade de ser 21 caras ou 20 caras e depois 1 coroa. Esses dois resultados são tão prováveis quanto qualquer uma das outras combinações que podem ser obtidas em 21 lançamentos de uma moeda. Todas as combinações de 21 lances terão probabilidades iguais a 0,521, ou 1 em 2.097.152. Assumir que uma mudança na probabilidade ocorrerá como resultado do resultado dos lançamentos anteriores é incorreto porque cada resultado de uma sequência de 21 lançamentos é tão provável quanto os outros resultados. De acordo com Bayes' teorema, o resultado provável de cada jogada é a probabilidade da moeda honesta, que é 1/2.
Outros exemplos
A falácia leva à noção incorreta de que as falhas anteriores criarão uma maior probabilidade de sucesso nas tentativas subsequentes. Para um dado justo de 16 lados, a probabilidade de cada resultado ocorrer é 1/16 (6,25%). Se uma vitória é definida como 1, a probabilidade de 1 ocorrer pelo menos uma vez em 16 jogadas é:
- 1- Sim. - Sim. Não.1516.]16.= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =64.39% % {displaystyle 1-left[{frac {15}{16}}right]^{16},=,64.39%}
A probabilidade de perder no primeiro lançamento é 15 /16 (93,75%). De acordo com a falácia, o jogador deveria ter uma chance maior de ganhar após a ocorrência de uma derrota. A probabilidade de pelo menos uma vitória é agora:
- 1- Sim. - Sim. Não.1516.]15= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =62.02% % {displaystyle 1-left[{frac {15}{16}}right]^{ 15},=,62.02%}
Ao perder um lance, a probabilidade de o jogador ganhar cai dois pontos percentuais. Com 5 derrotas e 11 jogadas restantes, a probabilidade de ganhar cai para cerca de 0,5 (50%). A probabilidade de pelo menos uma vitória não aumenta após uma série de derrotas; de fato, a probabilidade de sucesso na verdade diminui, porque restam menos tentativas para vencer. A probabilidade de ganhar eventualmente será igual à probabilidade de ganhar um único lance, que é 1/16 (6,25%) e ocorre quando resta apenas um lançamento.
Posição invertida
Depois de uma tendência consistente para coroa, um jogador também pode decidir que coroa se tornou um resultado mais provável. Esta é uma conclusão racional e bayesiana, tendo em vista a possibilidade da moeda não ser honesta; não é uma falácia. Acreditando que as probabilidades favorecem a coroa, o jogador não vê razão para mudar para cara. No entanto, é uma falácia que uma sequência de tentativas carrega uma memória de resultados passados que tendem a favorecer ou desfavorecer resultados futuros.
A falácia do jogador inverso descrita por Ian Hacking é uma situação em que um jogador que entra em uma sala e vê uma pessoa jogando um seis duplo em um par de dados pode concluir erroneamente que a pessoa deve ter jogado os dados por por um bom tempo, pois é improvável que consigam um duplo seis na primeira tentativa.
Falácia retrospectiva do jogador
Pesquisadores examinaram se existe um viés semelhante para inferências sobre eventos passados desconhecidos com base em eventos subsequentes conhecidos, chamando isso de "falácia do jogador retrospectivo".
Um exemplo da falácia de um jogador retrospectivo seria observar múltiplas "caras" em um cara ou coroa e conclua a partir disso que o lançamento anteriormente desconhecido foi "coroa". Exemplos do mundo real da falácia do jogador retrospectivo foram discutidos em eventos como a origem do Universo. Em seu livro Universos, John Leslie argumenta que "a presença de muitos universos muito diferentes em seus personagens pode ser nossa melhor explicação de por que pelo menos um universo tem um caráter que permite a vida".;. Daniel M. Oppenheimer e Benoît Monin argumentam que "Em outras palavras, a 'melhor explicação' para um evento de baixa probabilidade é que ele é apenas um em um múltiplo de tentativas, que é a intuição central da falácia do jogador reverso." Argumentos filosóficos estão em andamento sobre se tais argumentos são ou não uma falácia, argumentando que a ocorrência de nosso universo não diz nada sobre a existência de outros universos ou tentativas de universos. Três estudos envolvendo estudantes da Universidade de Stanford testaram a existência de um histórico retrospectivo de jogadores. falácia. Todos os três estudos concluíram que as pessoas têm uma personalidade de jogador. falácia retrospectivamente, bem como para eventos futuros. Os autores dos três estudos concluíram que suas descobertas têm "implicações metodológicas" significativas; mas também pode ter "implicações teóricas importantes" que precisam de investigação e pesquisa, dizendo "[uma] compreensão completa de tais processos de raciocínio requer que não apenas examinemos como eles influenciam nossas previsões do futuro, mas também nossas percepções do passado."
Parto
Em 1796, Pierre-Simon Laplace descreveu em A Philosophical Essay on Probabilities as maneiras pelas quais os homens calculavam sua probabilidade de ter filhos: "Eu vi homens, ardentemente desejosos de ter um filho, que só com ansiedade podia saber do nascimento de meninos no mês em que esperavam se tornar pais. Imaginando que a proporção desses nascimentos em relação aos de meninas deveria ser a mesma no final de cada mês, eles julgaram que os meninos já nascidos tornariam mais provável o próximo nascimento de meninas." Os futuros pais temiam que, se mais filhos nascessem na comunidade vizinha, eles próprios teriam mais chances de ter uma filha. Este ensaio de Laplace é considerado uma das primeiras descrições da falácia. Da mesma forma, depois de ter vários filhos do mesmo sexo, alguns pais podem acreditar erroneamente que devem ter um filho do sexo oposto.
Casino de Monte Carlo
Talvez o exemplo mais famoso da falácia do jogador tenha ocorrido em um jogo de roleta no Monte Carlo Casino em 18 de agosto de 1913, quando a bola caiu na cor preta 26 vezes seguidas. Esta foi uma ocorrência extremamente incomum: a probabilidade de uma sequência de vermelho ou preto ocorrer 26 vezes seguidas é (18/37)26-1 ou cerca de 1 em 66,6 milhões, supondo que o mecanismo seja imparcial. Os jogadores perderam milhões de francos apostando contra o preto, raciocinando incorretamente que a raia estava causando um desequilíbrio na aleatoriedade da roda e que deveria ser seguida por uma longa raia vermelha.
Não exemplos
Eventos não independentes
A falácia do apostador não se aplica quando a probabilidade de diferentes eventos não é independente. Nesses casos, a probabilidade de eventos futuros pode mudar com base no resultado de eventos passados, como a permutação estatística de eventos. Um exemplo é quando as cartas são retiradas de um baralho sem reposição. Se um ás for retirado de um baralho e não reinserido, é menos provável que a próxima carta retirada seja um ás e mais provável que seja de outro valor. A probabilidade de tirar outro ás, assumindo que foi a primeira carta tirada e que não há coringas, diminuiu de 4/52 (7,69%) para 3/51 (5,88 %), enquanto a probabilidade de cada classificação aumentou de 4 /52 (7,69%) a 4 /51 (7,84%). Este efeito permite que os sistemas de contagem de cartas funcionem em jogos como blackjack.
Viés
Na maioria das ilustrações da falácia do jogador e da falácia do jogador reverso, a tentativa (por exemplo, lançar uma moeda) é considerada justa. Na prática, essa suposição pode não se sustentar. Por exemplo, se uma moeda for lançada 21 vezes, a probabilidade de 21 caras com uma moeda honesta é de 1 em 2.097.152. Como essa probabilidade é tão pequena, se acontecer, pode ser que a moeda esteja de alguma forma inclinada a dar cara, ou que esteja sendo controlada por ímãs ocultos, ou algo semelhante. Nesse caso, a aposta inteligente é "cara" porque a inferência bayesiana da evidência empírica - 21 caras seguidas - sugere que a moeda provavelmente tende a ser cara. A inferência bayesiana pode ser usada para mostrar que, quando a proporção de longo prazo de diferentes resultados é desconhecida, mas permutável (o que significa que o processo aleatório a partir do qual os resultados são gerados pode ser tendencioso, mas tem a mesma probabilidade de ser tendencioso em qualquer direção) e que observações demonstram a provável direção do viés, o resultado que mais ocorreu nos dados observados é o mais provável de ocorrer novamente.
Por exemplo, se a probabilidade a priori de uma moeda viciada for, digamos, 1%, e assumindo que tal moeda viciada cairia cara, digamos 60% das vezes, então, após 21 caras, o probabilidade de uma moeda viciada aumentou para cerca de 32%.
A cena de abertura da peça Rosencrantz e Guildenstern Are Dead, de Tom Stoppard, discute essas questões enquanto um homem vira cabeças continuamente e o outro considera várias explicações possíveis.
Mudança de probabilidades
Se for permitido que fatores externos alterem a probabilidade dos eventos, a falácia do jogador pode não se sustentar. Por exemplo, uma mudança nas regras do jogo pode favorecer um jogador em detrimento do outro, melhorando sua porcentagem de vitórias. Da mesma forma, o sucesso de um jogador inexperiente pode diminuir depois que as equipes adversárias aprenderem e jogarem contra suas fraquezas. Este é outro exemplo de preconceito.
Psicologia
Origens
A falácia do jogador surge de uma crença em uma lei de pequenos números, levando à crença errônea de que pequenas amostras devem ser representativas da população maior. De acordo com a falácia, as estrias devem eventualmente se nivelar para serem representativas. Amos Tversky e Daniel Kahneman propuseram pela primeira vez que a falácia do jogador é um viés cognitivo produzido por uma heurística psicológica chamada heurística da representatividade, que afirma que as pessoas avaliam a probabilidade de um determinado evento avaliando o quão semelhante é aos eventos que eles têm experimentado antes, e quão semelhantes são os eventos que cercam esses dois processos. De acordo com essa visão, "depois de observar uma longa sequência de vermelho na roleta, por exemplo, a maioria das pessoas acredita erroneamente que o preto resultará em uma sequência mais representativa do que a ocorrência de um vermelho adicional", então as pessoas esperamos que um curto período de resultados aleatórios compartilhe as propriedades de um período mais longo, especificamente no sentido de que os desvios da média devem se equilibrar. Quando as pessoas são solicitadas a fazer uma sequência aleatória de lançamentos de moedas, elas tendem a fazer sequências em que a proporção de cara para coroa fica mais próxima de 0,5 em qualquer segmento curto do que seria previsto pelo acaso, um fenômeno conhecido como insensibilidade à amostra. tamanho. Kahneman e Tversky interpretam isso como significando que as pessoas acreditam que sequências curtas de eventos aleatórios devem ser representativas de sequências mais longas. A heurística da representatividade também é citada por trás do fenômeno relacionado da ilusão de agrupamento, segundo a qual as pessoas veem sequências de eventos aleatórios como não aleatórias quando, na verdade, essas sequências são muito mais prováveis de ocorrer em pequenas amostras do que as pessoas esperam.
A falácia do jogador também pode ser atribuída à crença errônea de que o jogo, ou mesmo o próprio acaso, é um processo justo que pode se corrigir em caso de sequências consecutivas, conhecida como hipótese do mundo justo. Outros pesquisadores acreditam que a crença na falácia pode ser o resultado de uma crença equivocada em um locus de controle interno. Quando uma pessoa acredita que os resultados do jogo são resultado de sua própria habilidade, ela pode ser mais suscetível à falácia do jogador porque rejeita a ideia de que o acaso pode superar a habilidade ou o talento.
Variações
Alguns pesquisadores acreditam que é possível definir dois tipos de falácia do jogador: tipo um e tipo dois. O tipo um é a falácia do jogador clássico, em que os indivíduos acreditam que um determinado resultado ocorre após uma longa sequência de outro resultado. A falácia do jogador tipo dois, conforme definido por Gideon Keren e Charles Lewis, ocorre quando um jogador subestima quantas observações são necessárias para detectar um resultado favorável, como assistir a uma roleta por um período de tempo e depois apostar no números que aparecem com mais frequência. Para eventos com alto grau de aleatoriedade, detectar um viés que levará a um resultado favorável leva um tempo impraticável e é muito difícil, se não impossível, de fazer. Os dois tipos diferem no tipo um assume erroneamente que as condições de jogo são justas e perfeitas, enquanto o tipo dois assume que as condições são tendenciosas e que esse viés pode ser detectado após um determinado período de tempo.
Outra variedade, conhecida como a falácia do jogador retrospectivo, ocorre quando os indivíduos julgam que um evento aparentemente raro deve vir de uma sequência mais longa do que um evento mais comum. A crença de que uma sequência imaginária de lançamentos de dados é mais de três vezes maior quando um conjunto de três seis é observado, em oposição a quando há apenas dois seis. Este efeito pode ser observado em instâncias isoladas, ou mesmo sequencialmente. Outro exemplo seria ouvir que uma adolescente fez sexo desprotegido e engravidou em uma determinada noite, e concluir que ela pratica sexo desprotegido há mais tempo do que se ouvíssemos que ela fez sexo desprotegido, mas não engravidou, quando a probabilidade de ficar grávida como resultado de cada relação sexual é independente da quantidade de relações sexuais anteriores.
Relação com a falácia da mão quente
Outra perspectiva psicológica afirma que a falácia do jogador pode ser vista como a contrapartida da falácia da mão quente do basquete, na qual as pessoas tendem a prever o mesmo resultado do evento anterior - conhecido como recência positiva - resultando na crença de que um artilheiro com pontuação alta continuará a marcar. Na falácia do jogador, as pessoas preveem o resultado oposto do evento anterior - recência negativa - acreditando que, como a roleta caiu no preto nas seis ocasiões anteriores, deve cair no vermelho na próxima. Ayton e Fischer teorizaram que as pessoas exibem recência positiva para a falácia da mão quente porque a falácia lida com o desempenho humano e que as pessoas não acreditam que um objeto inanimado possa se tornar "quente". O desempenho humano não é percebido como aleatório, e as pessoas são mais propensas a continuar em sequências quando acreditam que o processo que gera os resultados não é aleatório. Quando uma pessoa exibe a falácia do jogador, é mais provável que exiba também a falácia da mão quente, sugerindo que uma construção é responsável pelas duas falácias.
A diferença entre as duas falácias também é encontrada na tomada de decisões econômicas. Um estudo de Huber, Kirchler e Stockl em 2010 examinou como a mão quente e a falácia do jogador são exibidas no mercado financeiro. Os pesquisadores deram aos participantes uma escolha: eles poderiam apostar no resultado de uma série de lançamentos de moedas, usar a opinião de um especialista para influenciar sua decisão ou escolher uma alternativa sem risco em vez de uma recompensa financeira menor. Os participantes recorreram à opinião de especialistas para tomar sua decisão 24% das vezes com base em sua experiência anterior de sucesso, o que exemplifica a mão quente. Se o especialista estava correto, 78% dos participantes escolheram a opinião do especialista novamente, em oposição a 57% quando o especialista estava errado. Os participantes também exibiram a falácia do jogador, com a seleção de cara ou coroa diminuindo depois de perceber uma seqüência de qualquer resultado. Esse experimento ajudou a reforçar a teoria de Ayton e Fischer de que as pessoas depositam mais fé no desempenho humano do que em processos aparentemente aleatórios.
Neurofisiologia
Embora a heurística da representatividade e outros vieses cognitivos sejam a causa mais comumente citada da falácia do jogador, a pesquisa sugere que também pode haver um componente neurológico. A ressonância magnética funcional mostrou que depois de perder uma aposta ou aposta, conhecida como perda de risco, a rede frontoparietal do cérebro é ativada, resultando em mais comportamentos de risco. Em contraste, há diminuição da atividade na amígdala, caudado e estriado ventral após uma perda de risco. A ativação na amígdala está negativamente correlacionada com a falácia do jogador, de modo que quanto mais atividade exibida na amígdala, menor a probabilidade de um indivíduo ser vítima da falácia do jogador. Esses resultados sugerem que a falácia do jogador depende mais do córtex pré-frontal, responsável pelos processos executivos direcionados a objetivos, e menos das áreas cerebrais que controlam a tomada de decisão afetiva.
O desejo de continuar jogando ou apostando é controlado pelo corpo estriado, que dá suporte a um método de aprendizado de contingência de escolha e resultado. O corpo estriado processa os erros de previsão e o comportamento muda de acordo. Após uma vitória, o comportamento positivo é reforçado e após uma derrota, o comportamento é condicionado a ser evitado. Em indivíduos que exibem a falácia do jogador, esse método de contingência de escolha de resultado é prejudicado e eles continuam a arriscar após uma série de perdas.
Possíveis soluções
A falácia do jogador é um viés cognitivo arraigado e pode ser muito difícil de superar. Educar os indivíduos sobre a natureza da aleatoriedade nem sempre se mostrou eficaz na redução ou eliminação de qualquer manifestação da falácia. Os participantes de um estudo de Beach e Swensson em 1967 viram um baralho de fichas embaralhadas com formas nelas e foram instruídos a adivinhar qual forma viria a seguir em uma sequência. O grupo experimental de participantes foi informado sobre a natureza e a existência da falácia do jogador e foi explicitamente instruído a não confiar na dependência de execução para fazer suas suposições. O grupo de controle não recebeu essa informação. Os estilos de resposta dos dois grupos foram semelhantes, indicando que o grupo experimental ainda baseava suas escolhas na duração da sequência de execução. Isso levou à conclusão de que instruir os indivíduos sobre a aleatoriedade não é suficiente para diminuir a falácia do jogador.
A suscetibilidade de um indivíduo à falácia do jogador pode diminuir com a idade. Um estudo de Fischbein e Schnarch em 1997 administrou um questionário a cinco grupos: alunos da 5ª, 7ª, 9ª e 11ª séries e estudantes universitários especializados em ensino de matemática. Nenhum dos participantes havia recebido qualquer educação prévia sobre probabilidade. A pergunta feita foi: "Ronni jogou uma moeda três vezes e em todos os casos saiu cara. Ronni pretende jogar a moeda novamente. Qual é a chance de obter cara na quarta vez?" Os resultados indicaram que, à medida que os alunos envelheciam, era menos provável que respondessem com "menor do que a chance de obter coroa", o que indicaria um efeito de recência negativo. 35% dos alunos do 5º ano, 35% dos alunos do 7º ano e 20% dos alunos do 9º ano exibiram o efeito de recência negativo. Apenas 10% dos alunos do 11º ano responderam dessa forma, e nenhum dos universitários o fez. Fischbein e Schnarch teorizaram que a tendência de um indivíduo de confiar na heurística da representatividade e em outros vieses cognitivos pode ser superada com a idade.
Outra solução possível vem de Roney e Trick, psicólogos da Gestalt que sugerem que a falácia pode ser eliminada como resultado do agrupamento. Quando um evento futuro, como o lançamento de uma moeda, é descrito como parte de uma sequência, não importa o quão arbitrário, uma pessoa considerará automaticamente o evento em relação aos eventos passados, resultando na falácia do jogador. Quando uma pessoa considera cada evento como independente, a falácia pode ser bastante reduzida.
Roney e Trick disseram aos participantes em seu experimento que estavam apostando em dois blocos de seis lançamentos de moedas ou em dois blocos de sete lançamentos de moedas. O quarto, quinto e sexto lances tiveram todos o mesmo resultado, três caras ou três coroas. O sétimo lançamento foi agrupado com o final de um bloco ou o início do próximo bloco. Os participantes exibiram a falácia do apostador mais forte quando a sétima tentativa fazia parte do primeiro bloco, logo após a sequência de três caras ou coroas. Os pesquisadores apontaram que os participantes que não apresentaram a falácia do jogador mostraram menos confiança em suas apostas e apostaram menos vezes do que os participantes que escolheram com a falácia do jogador. Quando a sétima tentativa foi agrupada com o segundo bloco e foi percebida como não fazendo parte de uma sequência, a falácia do apostador não ocorreu.
Roney e Trick argumentaram que, em vez de ensinar os indivíduos sobre a natureza da aleatoriedade, a falácia poderia ser evitada treinando as pessoas para tratar cada evento como se fosse um começo e não uma continuação de eventos anteriores. Eles sugeriram que isso evitaria que as pessoas jogassem quando estivessem perdendo, na esperança equivocada de que suas chances de ganhar aumentassem com base na interação com eventos anteriores.
Usuários
Tipos de usuários
Dentro de um cenário do mundo real, vários estudos descobriram que, para vários tomadores de decisão colocados em cenários de alto risco, é provável que eles reflitam algum grau de forte autocorrelação negativa em seu julgamento.
Juízes de asilo
Em um estudo destinado a descobrir se a autocorrelação negativa que existe com a falácia do jogador existia na decisão de juízes de asilo dos Estados Unidos, os resultados mostraram que, após duas concessões de asilo sucessivas, um juiz teria 5,5% menos probabilidade para aprovar uma terceira concessão.
Árbitros de beisebol
No jogo de beisebol, as decisões são tomadas a cada minuto. Uma decisão particular tomada pelos árbitros que está frequentemente sujeita a escrutínio é a decisão da 'zona de rebatida'. Sempre que um rebatedor não balançar, o árbitro deve decidir se a bola estava dentro de uma região justa para o rebatedor, conhecida como zona de strike. Se fora desta zona, a bola não conta para a saída do rebatedor. Em um estudo de mais de 12.000 jogos, os resultados mostraram que os árbitros têm 1,3% menos probabilidade de marcar um strike se as duas bolas anteriores também foram strikes.
Oficiais de empréstimo
Na tomada de decisão dos oficiais de crédito, pode-se argumentar que os incentivos monetários são um fator-chave na tomada de decisão tendenciosa - tornando difícil examinar o efeito da falácia do jogador. No entanto, a pesquisa mostra que os agentes de crédito que não são incentivados por ganhos monetários têm 8% menos probabilidade de aprovar um empréstimo se aprovarem um para o cliente anterior.
Jogadores de loteria
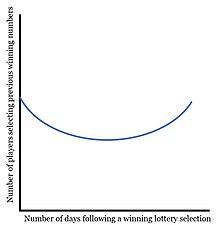
Jogos de loteria e jackpots atraem apostadores em todo o mundo, com a maior decisão para os vencedores esperançosos sendo quais números escolher. Embora a maioria das pessoas tenha sua própria estratégia, as evidências mostram que depois que um número é selecionado como vencedor no sorteio atual, o mesmo número sofrerá uma queda significativa nas seleções na loteria seguinte. Um estudo popular de Charles Clotfelter e Philip Cook investigou esse efeito em 1991, onde concluíram que os apostadores parariam de selecionar números imediatamente após serem selecionados - recuperando a popularidade da seleção em três meses. Logo depois, um estudo de 1994 foi elaborado por Dek Terrell para testar as descobertas de Clotfelter e Cook. A principal mudança no estudo de Terrell foi o exame de uma loteria pari-mútua na qual um número selecionado com apostas totais mais baixas resultará em um pagamento maior. Embora esse exame tenha concluído que os jogadores de ambos os tipos de loterias exibiam um comportamento alinhado com a teoria da falácia do jogador, aqueles que participavam de apostas mútuas pareciam ser menos influenciados.
| Grande aposta por jogadores de loteria | ||||||
|---|---|---|---|---|---|---|
| Números sorteados 14 de Abril de 1988 | Dia de desenho | Dias após sorteio | ||||
| Abril | Números do vencedor | 0 | 1 | 3 | 7 | 56 |
| 11 | 244 | 41 | 34 | 24. | 27 | 30 |
| 12 | 504 | 29 de Março | 20. | 12 | 18. | 15 |
| 13 | 718 | 28 | 20. | 17. | 19 | 25 |
| 14 | 323 | 134 | 95 | 79 | 81 | 76 |
| 15 | 640 | 10. | 20. | 18. | 16. | 20. |
| 16. | 957 | 30 | 22 | 20. | 24. | 32 |
| Percentagem média de jogadores que selecionam anteriormente
números vencedores em comparação com o dia do sorteio | 78% | 63% | 68% | 73% | ||
O efeito da falácia do apostador pode ser observado quando os números são escolhidos com muito menos frequência logo após serem selecionados como vencedores, recuperando-se lentamente ao longo de um período de dois meses. Por exemplo, em 11 de abril de 1988, 41 jogadores selecionaram 244 como a combinação vencedora. Três dias depois, apenas 24 indivíduos selecionaram 244, uma redução de 41,5%. Essa é a falácia do apostador em movimento, pois os apostadores acreditam que a ocorrência de uma combinação vencedora em dias anteriores diminuirá sua probabilidade de ocorrer hoje.
Jogadores de videogame
Vários videogames apresentam o uso de loot boxes, uma coleção de itens do jogo concedidos na abertura com conteúdo aleatório definido por métricas de raridade, como um esquema de monetização. Desde cerca de 2018, as loot boxes estão sob escrutínio de governos e defensores por serem semelhantes a jogos de azar, principalmente para jogos voltados para jovens. Alguns jogos usam um "temporizador de pena" mecanismo, que se o jogador abriu várias caixas de saque seguidas sem obter um item de alta raridade, as caixas de saque subsequentes aumentarão as chances de queda de um item de taxa mais alta. Considera-se que isso alimenta a falácia do jogador, pois reforça a ideia de que um jogador eventualmente obterá um item de alta raridade (uma vitória) depois de receber apenas itens comuns de uma série de caixas de saque anteriores.
Contenido relacionado
Introdução bicondicional
Loglan
Análise de variação



![1-left[frac{15}{16}right]^{16} ,=, 64.39%](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d791f63cddc590830c6ef468bbf823c14c1953f)
![1-left[frac{15}{16}right]^{15} ,=, 62.02%](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b0b7ce6d128c5742499914574afc8e625b73af1)